Вывод уравнения Лапласа. Плоские задачи теории фильтрации

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Курсовая работа

По курсу «Подземная гидромеханика»

Тема: «Вывод уравнения Лапласа. Плоские задачи теории фильтрации»

2009

Содержание

Введение

1. Дифференциальные уравнения движения сжимаемой и несжимаемой жидкости в пористой среде. Вывод уравнения Лапласа.

2. Плоские задачи теории фильтрации

2.1 Приток к совершенной скважине

2.1.1 Фильтрационный поток от нагнетательной скважины к эксплуатационной

2.1.2 Приток к группе скважин с удаленным контуром питания

2.1.3 Приток к скважине в пласте с прямолинейным контуром питания

2.1.4 Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы

2.1.5 Приток к скважине в пласте с произвольным контуром питания

2.1.6 Приток к бесконечным цепочкам и кольцевым батареям скважин

2.1.6.1 Приток к скважинам кольцевой батареи

2.1.6.2 Приток к прямолинейной батареи скважин

2.1.7 Метод эквивалентных фильтрационных сопротивлений

Вывод

Литература

Введение

Подземная гидромеханика — наука о движении жидкостей, газов и их смесей в пористых и трещиноватых горных породах — теоретическая основа разработки нефтяных и газовых месторождений, одна из профилирующих дисциплин в учебном плане промыслового и геологического факультетов нефтяных вузов.

В основе подземной гидравлики лежит представление о том, что нефть, газ и вода, заключенные в пористой среде, составляют единую гидравлическую систему.

Теоретической основой ПГД является теория фильтрации - наука, описывающая данное движение флюида с позиций механики сплошной среды, т.е. гипотезы сплошности (неразрывности) течения.

Особенностью теории фильтрации нефти и газа в природных пластах является одновременное рассмотрение процессов в областях, характерные размеры которых различаются на порядки: размер пор (до десятков микрометров), диаметр скважин (до десятков сантиметров), толщины пластов (до десятков метров), расстояния между скважинами (сотни метров), протяженность месторождений (до сотен километров).

В данной курсовой работе выводится основное уравнение Лапласа и рассматриваются плоские задачи теории фильтрации, а так же их решение.

1. Дифференциальные уравнения движения сжимаемой и несжимаемой жидкости в пористой среде. Вывод уравнения Лапласа

При выводе дифференциального уравнения движения сжимаемой жидкости исходными уравнениями являются следующие:

закон фильтрации жидкости; в качестве закона фильтрации принимаем линейный закон фильтрации, выражающийся формулами (3.1)

, (3.1)

уравнение неразрывности (3.2)

, (3.2)

уравнение состояния. Для капельной сжимаемой жидкости уравнение состояния может быть представлено в виде (3.3)

, (3.3)

где 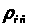- плотность жидкости при атмосферном давлении .

Подставляя в уравнение неразрывности (3.2) вместо проекций скорости фильтрации vx, vy и vz их значения из линейного закона, выражающегося формулой (3.1), получим:

, (3.4)

уравнения состояния (3.3) имеем:

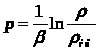, (3.5)

Откуда

,

,

. (3.6)

Подставляя эти значения частных производных 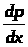, 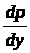и в уравнение (3.4), получим:

Вводя оператор Лапласа

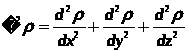
уравнение (3.7) более кратко можно написать в виде

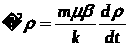, (3.8)

Учитывая, что

, (3.9)

уравнение (3.7) можно приближенно представить в виде:

,(3.10)

Уравнение (3.7) или приближенное заменяющее его уравнение (3.10) есть искомое дифференциальное уравнение неустановившегося движения сжимаемой жидкости в пористой среде. Упомянутые уравнения имеют вид «уравнения теплопроводности», интегрирование которого при различных начальных и граничных условиях рассматривается в каждом курсе математической физики.

Решение различных задач о неустановившемся движении однородной сжимаемой жидкости в пористой среде, основанное на интегрировании уравнения (3.7) при различных начальных и граничных условиях, дается в книгах В. Н. Щелкачева, И. А. Чарного и М.Маскета. При установившемся движении сжимаемой жидкости и вместо уравнения (3.7) имеем:

, (3.11)

Уравнение (3.11) называется уравнением Лапласа.

При установившейся и неустановившейся фильтрации несжимаемой жидкости плотность жидкости постоянна следовательно, величина, стоящая в правой части уравнения (3.4), равна нулю. Сокращая левую часть этого уравнения на постоянную и выполнив дифференцирование, получим:

, (3.12)

Таким образом, установившаяся и неустановившаяся фильтрация несжимаемой жидкости описывается уравнением Лапласа (3.12).

2. Плоские задачи теории фильтрации

При разработке нефтяных и газовых месторождений (НГМ) возникает два вида задач:

1. Задаётся дебит скважин и требуется определить необходимое для этого дебита забойное давление и, кроме того, давление в любой точке пласта. В данном случае величина дебита определяется значением предельной для имеющихся коллекторов депрессией, при которой ещё не наступает их разрушение, или прочностными характеристиками скважинного оборудования, или физическим смыслом. Последнее означает, например, невозможность установления нулевого или отрицательного забойного давления.

2. Задаётся забойное давление и требуется определить дебит. Последний вид условия встречается наиболее часто в практике разработки НГМ. Величина забойного давления определяется условиями эксплуатации. Например, давление должно быть больше давления насыщения для предотвращения дегазации нефти в пласте или выпадения конденсата при разработке газоконденсатных месторождений, что снижает продуктивные свойства скважин. Наконец, если возможен вынос песка из пласта на забой скважины, то скорость фильтрации на стенке скважины должна быть меньше некоторой предельной величины.

Замечено, что при эксплуатации группы скважин в одинаковых условиях, т.е. с одинаковым забойным давлением, дебит всего месторождения растёт медленнее увеличения числа новых скважин с теми же забойными условиями (рис.4.1). Увеличение дебита при этом требует понижения забойного давления.

Для решения поставленных задач решим задачу плоской интерференции (наложения) скважин. Предположим, что пласт - неограниченный, горизонтальный, имеет постоянную мощность и непроницаемые подошву и кровлю. Пласт вскрыт множеством совершенных скважин и заполнен однородной жидкостью или газом. Движение жидкости - установившееся, подчиняется закону Дарси и является плоским. Плоское движение означает, что течение происходит в плоскостях, параллельных между собой и картина движения во всех плоскостях идентична. В связи с этим разбирается течение в одной из этих плоскостей - в основной плоскости течения.

Решение задач будем строить на принципе суперпозиции (наложения) потоков. Основанный на этом принципе метод суперпозиции заключается в следующем.

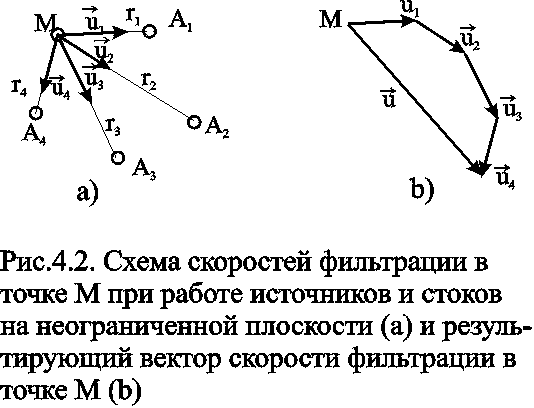
При совместном действии в пласте нескольких стоков (эксплуатационных скважин) или источников (нагнетательных скважин) потенциальная функция, определяемая каждым стоком (источником), вычисляется по формуле для единственного стока (источника). Потенциальная функция, обусловленная всеми стоками (источниками), вычисляется путём алгебраического сложения этих независимых друг от друга значений потенциальной функции. Суммарная скорость фильтрации определяется как векторная сумма скоростей фильтрации, вызванная работой каждой скважины (рис.4.2b).

Пусть в неограниченном пласте действует n стоков с положительным массовым дебитом G и источников с отрицательным дебитом (рис. 4.2a).. Поток в окрестности каждой скважины в этом случае плоскорадиален и потенциал

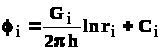,(4.1)

где i - номер скважины; ri - расстояние между некоторой точкой пласта М и центром скважины под номером i.

Пользуясь методом суперпозиции, определим потенциал сложного потока

,(4.2)

где

.

Зависимость (4.2) физически означает, что фильтрационные потоки от работы каждого источника-стока накладываются друг на друга. Т.к. пласт предполагается неограниченным, то потенциал на бесконечности равен бесконечности. В центрах стоков-источников (ri=0) потенциал также равен бесконечности.

Если жидкость несжимаема, то вместо массовых дебитов можно использовать объёмные дебиты Q в зависимости (4.2).

Для определения уравнений эквипотенциальных поверхностей (изобар) следует иметь в виду, что во всех точках этих кривых значение потенциала (давления) должно оставаться неизменным. Т.о. приравнивая (4.2) к некоторой постоянной получим

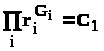,(4.3)

где П - знак произведения; С1 - постоянная.

Если дебиты всех скважин равны по величине, то

,(4.4)

Линии тока образуют семейство кривых, ортогональных изобарам.

Метод суперпозиции можно использовать не только в бесконечных пластах, но и в пластах, имеющих контур питания или непроницаемую границу произвольной формы. В этом случае для выполнения тех или иных условий на границах вводятся фиктивные стоки или источники за пределами пласта. Фиктивные скважины в совокупности с реальными обеспечивают необходимые условия на границах и задача сводится к рассмотрению одновременной работы реальных и фиктивных скважин в неограниченном пласте. Данный метод называется методом отображения источников и стоков.

2.1 Приток к совершенной скважине

Формула (4.2) основная в решении задач интерференции скважин. Рассмотрим применение этой формулы в случаях: фильтрационного потока от нагнетательной скважины к эксплуатационной; пласта с произвольным контуром питания, но удалённым от скважин и пласта с прямолинейным контуром питания.

2.1.1 Фильтрационный поток от нагнетательной скважины к эксплуатационной

Пусть сток О1 и источник О2 равнодебитны, т.е. имеют одинаковые по модулю массовые дебиты G. Расстояние между источником и стоком равно 2а. Исследуем поток от источника к стоку.

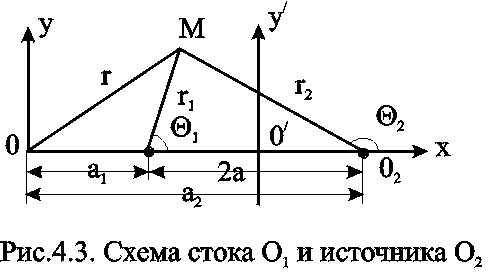
Проведём ось 0 х через точки О1 и О2 таким образом, чтобы точка О1 находилась от начала координат 0 на расстоянии а1, а точка О2 на расстоянии а2 (рис. 4.3).

По формуле (4.2) определим потенциальную функцию потока. При этом учтем знаки дебитов: источник G 1= - G, а сток G 2= + G. После подстановки получим:

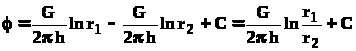,(4.5)

где r1 и r2 - расстояния любой точки пласта до стока и источника, соответственно.

Уравнение изобар (4.4) при этом будет иметь вид

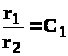(4.6)

и соответствует окружностям, центры которых расположены на оси 0х. Если поместим начало координат в центре какой-либо окружности семейства, то радиус данной окружности определится выражением

,(4.7)

а коэффициент

. (4.8)

Подставляя С1 в (4.7) найдем

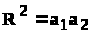. (4.9)

Из (4.9) видно, что a1 < R < a2 или a1 > R > a2 ; следовательно, все окружности пересекают ось между стоком и источником, а значит, одна из особых точек находится внутри окружности данного радиуса R, другая - вне этой окружности. Точки О1 и О2 , положения которых на прямой 0х определяются равенством (4.7), называются взаимосимметричными относительно окружности радиуса R.

Допустим, что радиус R=, т.е. берём ту эквипотенциальную линию, которая является прямой. Из (4.7) следует, что в этом случае С1=1 и, как следует из (4.6), r1=r2 . Последнее равенство означает, что в числе эквипотенциальных линий есть прямая 0у, которая делит расстояние между стоком и источником пополам и параллельна оси 0у (рис.4.3).

Итак, эквипотенциальные линии (изобары) при совместном действии одной эксплуатационной и одной нагнетательной скважин в неограниченном пласте представляют собой окружности, центры которых расположены на прямой, проходящей через центры скважин (рис.4.4).. Среди окружностей есть одна, имеющая бесконечно большой радиус - прямая, которая делит расстояние между скважинами и всю плоскость течения пополам. Половина всех окружностей конечного радиуса R расположена по одну сторону от этой прямой, остальные окружности - по другую.

Семейство линий тока ортогонально изобарам и, следовательно, в данном случае тоже окружности. Все линии тока проходят через сток и источник. Центры всех окружностей линий тока расположены на прямой, делящей расстояние между стоком и источником пополам (рис.4.4).

Массовый дебит эксплуатационной и нагнетательной скважин при их совместной деятельности определяется на основе соотношения (4.5), расписанного для каждой скважины при учете отношений радиусов (рис.4.3): на контуре эксплуатационной скважины - ; на контуре нагнетательной скважины - . Решая, полученную систему уравнений, имеем

. (4.10)

Массовая скорость фильтрации в любой точке пласта М (рис.4.2) находится по правилу суперпозиции сложения векторов скорости от действия источника и стока

. (4.11)

Величина корня есть расстояние между источником и стоком 2а и, следовательно, формула (4.11) перепишется в виде

, (4.12)

Для поддержания пластового давления часто используется нагнетание воды в пласт. Определим для однородной несжимаемой жидкости время движения частицы по кратчайшему пути между нагнетательной и эксплуатационной скважинами, т.е. по оси 0х. При жестководонапорном режиме решается при этом вопрос о времени, протекшем от начала закачки воды в пласт до начала её прорыва в эксплуатационную скважину.

Чтобы решить указанную задачу выразим скорость в (4.12) через производную расстояния по времени и, поместив начало координат в сток О1 , проинтегрируем полученное уравнение по х от х0 до х. Тогда время движения частицы от некоторой точки х0 до точки х определится зависимостью

. (4.13)

Время обводнения Т, т.е. прохождения частицы расстояния О1О2= 2а определится из (4.13), если принять х=0; х0=2а

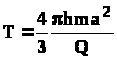, (4.14)

где m - пористость; Q - объёмный дебит.

Зная Т можно найти площадь обводнения , приравнивая объёмы TQ и mh. Откуда

,(4.15)

Анализ формул (4.13) и (4.14) показывает, что расстояние, пройденное частицей за время Т от нагнетательной скважины до эксплуатационной, вдвое больше расстояния пройденного другой частицей за это же время в положительном направлении оси х.

4.1.2 Приток к группе скважин с удаленным контуром питания

В большинстве практических случаев контур питания находится довольно далеко. Поэтому решения данной задачи позволяют провести предварительную оценку однородных участков месторождений.

Пусть в пласте расположена группа из n скважин (рис. 4.5) с различными для общности дебитами Gi, забойными потенциалами pi и радиусами скважин ri. Расположение скважин задано и на достаточно большом удалении находится контур питания, форма которого неизвестна, но известен порядок расстояния rк от контура питания до группы скважин При этом rк на много больше расстояния между скважинами. Считаем, что дан потенциал контура  к и забойные потенциалы скважин  i.

Для определения дебитов используем формулу (4.2) при помещении точки М на забое каждой скважины, что позволяет записать n - уравнений вида

, (4.16)

где rci - радиус скважины на которую помещена точка М; rji - расстояние между i - ой и j - ой скважинами; ci - забойный потенциал i - ой скважины.

Неизвестных же - n+1, так как константа тоже неизвестна. Для нахождения константы С воспользуемся условием =к на удалённом контуре питания:

, (4.17)

Приближение заключается в том, что для удаления точек контура питания от скважин принимаем одно и тоже расстояние rк , что справедливо для достаточного удаления контура, учитывая что оно находится под знаком логарифма. Уравнение (4.17) и будет (n+1 ) уравнением.

Таким образом плоская задача интерференции при удалённом контуре питания сводится к решению алгебраической системы уравнений первой степени (4.16),(4.17).

При помощи данной системы можно находить или депрессию при заданном дебите, или получить значения дебитов при заданных депрессиях. При найденных дебитах можно определить пластовое давление в любой точке по (4.2), причем результат будет тем точнее, чем дальше эта точка отстоит от контура питания.

2.1.3 Приток к скважине в пласте с прямолинейным контуром питания

Пусть в полосообразном пласте пробурена одна скважина с центром в точке О1 на расстоянии а от прямолинейного контура (ось у ) бесконечного протяжения, на котором поддерживается постоянный потенциал к . На скважине радиуса rc поддерживается постоянный потенциал с. Найдём дебит скважины G и распределение функции .

Так как контур питания пласта 0у является эквипотенциальной линией, то все линии тока, сходящиеся в центре скважины О1, должны быть перпендикулярны к прямой 0у (рис.4.6). Для определения поля течения добьёмся выполнения граничных условий на контуре введением фиктивного источника О2 с дебитом, равным дебиту стока О1, путём зеркального отображения данного стока относительно прямой 0у.Т.о. используем ранее упомянутый метод отображения и задачу о потоке в пласте с прямолинейным контуром питания и с одиночной эксплуатационной скважиной сведём к ранее рассмотренной в разделе 4.1.1. задаче о совместном действии источника и стока равной производительности. Отличие данных задач только в постановке граничных условий: в задаче раздела 4.1.1. источник питания - нагнетательная скважина, а в данном случае - прямолинейный контур, а источник О2 фиктивный.

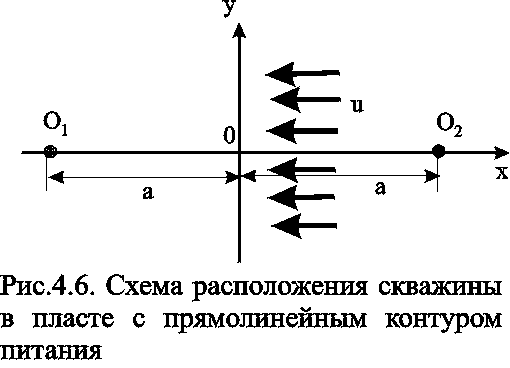
Т.о. используем для определения дебита выражение (4.10), но со следующей заменой граничных условий: =к при r1=r2 ,т.е. при r1/r2=1; =с при r1=rс , r22а, т.е. при r1/r2 rс /2а;

Подставляя последовательно соответствующие граничные значения , r1 и r2 в равенство (4.10) получим два уравнения, определяющих потенциалы на контуре и забое. Из этих уравнений легко находится массовый дебит одиночной скважины в пласте с прямолинейным контуром

.(4.18)

Если бы в пласте была нагнетательная скважина, то в формуле (4.18) достаточно только изменить знак правой части.

2.1.4 Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы

Данная задача может возникнуть при расположении добывающей скважины вблизи сброса или около границы выклинивания продуктивного пласта. В этом случае реальную скважину-сток зеркально отображают относительно непроницаемой границы, и дебиту скважины - отображения приписывают тот же знак, что и дебиту реальной скважины. При притоке к двум равнодебитным скважинам скорость фильтрации на непроницаемой границе будет направлена вдоль границы, т.е. граница является линией тока и фильтрация через неё отсутствует. Дебит скважины определяется из уравнений (4.16) и (4.17) для n=2 в пласте с удалённым контуром питания:

.(4.19)

2.1.5 Приток к скважине в пласте с произвольным контуром питания

В естественных условиях контур питания имеет произвольную форму и её не всегда удаётся определить. Кроме того, часто не удаётся определить достаточно точно и расстояние а от скважины О1 до контура. Можно ли в этом случае пользоваться формулой предыдущего раздела? Любой произвольный контур В находится между прямолинейным Впр и круговым Вкр. (рис.4.7).

Расчеты дебитов проведенные для этих двух крайних разновидностях контуров показали:

При вычислении дебита скважины форма внешнего контура пласта не имеет сколько-нибудь существенного значения.

Чем дальше от внешнего контура пласта находится скважина, тем меньший дебит она имеет. Однако, так как величина расстояния входит под знаком логарифма, то даже значительное изменение этого расстояния мало влияет на величину дебита

В случае расположения скважины эксцентрично относительно контура поток можно считать плоско-радиальным и дебит рассчитывать по формуле Дюпюи если rк.>103 rc и эксцентриситет а1< rк /2.

Таким образом, для практических расчетов точное знание формы и расстояния до контура питания необязательно, но порядок расстояния до контура питания должен быть известен.

2.1.6 Приток к бесконечным цепочкам и кольцевым батареям скважин

Рассмотрим многорядные батареи скважин. Решение задачи об интерференции скважин в пласте с удаленным контуром питания показывает, что в общем случае приходится решать столько уравнений, сколько имеется скважин. Следовательно, для получения точного решения необходимо использование ЭВМ, т.к. на месторождениях имеется десятки и сотни скважин, но можно воспользоваться с достаточной для практики точностью приближенным решением данной задачи.

При рациональной системе разработки скважины располагают обычно в виде рядов, расставленных вдоль контура нефте-газоносности и контура питания. Эти линии называются батареями или рядами скважин. Без большой погрешности можно считать дебит скважин в каждом ряду одинаковым, если в каждом ряду скважины находятся в одинаковых условиях. Дебиты же скважин в разных рядах будут отличаться друг от друга. Наибольший дебит имеет первый ряд, ближайший к контуру питания, а по мере удаления дебит уменьшается. Поэтому число одновременно работающих рядов редко превышает двух-трёх и последующие ряды включаются по мере приближения контура нефте-газоносности. Когда вода подошла к первому ряду, то он выключается и включается один из следующих рядов и т.д.

В этом случае число неизвестных уменьшается от числа скважин n до числа рядов N (обычно число рядов не превышает 2-4), а это уже гораздо более простая задача.

2.1.6.1 Приток к скважинам кольцевой батареи

Пусть центры скважин располагаются в вершинах правильного n-угольника, т.к. что скважины образуют кольцевую батарею радиуса а (рис. 4.8). Контур питания удалён от скважин на расстояние, значительно превышающее радиус батареи и тогда можно считать, что все скважины равноудалены от контура питания на расстояние rк. Будем считать, что на контуре питания поддерживается постоянное значение потенциала к и на контуре скважин потенциал постоянен и равен с. В данной постановке следовательно надо решить задачу о плоском течении к n точечным стокам, размещённым равномерно на окружности радиуса а. Для получения формулы дебита скважин воспользуемся формулой (4.2)

,(4.20)

где G - массовый дебит любой скважины батареи, rj - расстояния от некоторой точки пласта до всех n скважин; h - толщина пласта.

Граничные условия:

на контуре питания =к=const при rj=rк;

на контуре скважины =с=const при r1=rс;

rj(j1)=2a sin[(n-1)/n].

Используя данные граничные условия преобразуем формулу (4.20)

, (4.21)

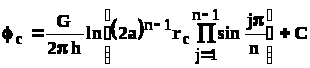. (4.22)

В последнем выражении

. (4.23)

Тогда (4.22) перепишется в виде

,(4.24)

и из (4.21), (4.24) получим выражение для определения дебита скважины

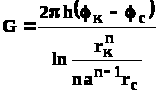,(4.25)

Формула (4.25) справедлива при любом целом n. В частности, при n=1 имеем выражение типа формулы Дюпюи для определения дебита при плоскорадиальном потоке:

.(4.26)

Формула (4.25) - приближенная. Её можно применять в случае, если размеры пласта во много раз больше площади внутри окружности батареи скважин, например, при водонапорном режиме, когда жидкость можно считать несжимаемой. Если же в пласте установился режим растворенного газа, то трудно ожидать, что площадь, занятая газированной жидкостью, простирается до границ пласта. Если расстояние до контура незначительно превышает радиус батареи, то, строго говоря, следует воспользоваться более точной формулой

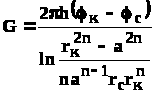,(4.27)

Эта формула при n=1 переходит в формулу определения дебита эксцентрично заложенной одиночной скважины (а - эксцентриситет скважины). В большинстве практических случаев можно пользоваться формулой (4.25), т.к. уже при rк=10а, дебиты подсчитанные по формулам (4.24) и (4.27), различаются не более чем на одну тысячную процента.

Определим дебит батареи умножив формулу (4.25) на число скважин в батареи n

.(4.28)

Рассмотрим поле течения в области действия круговой батареи, т.е. построим семейства линий тока и изобар. Уравнение изобар получаем из (4.3) путём представления радиусов rj в полярной системе координат (рис. 4.8)

. (4.29)

Данное уравнение позволяет построить поле изобар, а линии тока пересекают изобары под прямым углом.

Плоскость течения (рис. 4.9) кольцевой батареи с n равнодебитными скважинами, размещенными в вершинах правильного многоугольника, делится на n равных частей (секторов) прямыми линиями тока Н, сходящимися в центре батареи и делящими расстояние между двумя соседними скважинами пополам. Эти линии тока называются нейтральными. Другое семейство прямых линий тока Г проходит через центры скважин и делит сектор, ограниченный двумя нейтральными линиями, пополам. Это - главные линии.

Семейство изобар подразделяется на два подсемейства, которые разграничиваются изобарой пересекающей себя в центре батареи столько раз сколько скважин составляет данную батарею. Первое подсемейство изобар определяет приток к отдельным скважинам и представляет собой замкнутые, каплеобразные кривые, описанные вокруг каждой скважины. Второе семейство - определяет приток к батареи в целом и представляет собой замкнутые кривые, описанные вокруг батареи.

Скорость фильтрации по главным линиям максимальна, а по нейтральным линиям - минимальна. В центре кольцевой батареи скорость фильтрации равна нулю, т.е. частица жидкости, находящаяся в точке, в которой изобара пересекает сама себя, неподвижна. Такие точки фильтрационного поля называются точками равновесия и при разработке в окрестностях таких точек образуются “застойные области”. В условиях водонапорного режима в этих областях могут возникать “целики нефти”. Зная положения точек равновесия в пласте, можно находить рациональные приёмы для своевременной ликвидации целиков нефти. Одним из таких приёмов является изменение режима работы скважин, заставляющее нефть целика прийти в движение в нужном направлении.

Для кольцевой батареи, на основе анализа формул (4.25)-(4.28), можно сделать ряд оценок эффекта взаимодействия:

дебит изменяется непропорционально числу скважин и радиусу батареи (расстоянию между скважинами);

с увеличением числа скважин дебит каждой скважины уменьшается при постоянном забойном давлении, т.е. растет эффект взаимодействия;

взаимодействие скважин может практически не проявляться только при очень больших расстояниях между скважинами (в случае несжимаемой жидкости, строго говоря, влияние скважин распространяется на весь пласт);

с увеличением числа скважин темп роста суммарного дебита батареи замедляется (рис. 4.1), а именно, сверх определённого предела увеличение числа скважин оказывается неэффективным в виду прекращения прироста дебита виду прекращения прироста дебита.

2.1.6.2 Приток к прямолинейной батареи скважин

Рассмотрим, как и в предыдущем случае, приток к батареи при удалённом контуре питания в режиме поддержания постоянного забойного давления. В отличии от круговой батареи необходимо различать два случая:

число скважин батареи нечетное;

число скважин четное.

В обоих случаях дебиты скважин, равноудаленные от середины или от концов батареи, будут одинаковы, а при разной удаленности будут отличаться. Последнее вызывается не одинаковой интенсивностью влияния со стороны скважин батареи на те или иные скважины. При этом при нечетном числе скважин дебит средней скважины отличается от дебитов других скважин.

Дебиты равномерно расположенных скважин можно определить общим методом с использованием формулы (4.2). Можно вывести аналогичные уравнения для любой скважины прямолинейной батареи конечной длины в пласте с прямолинейным контуром питания, но с использованием дополнительно метода отображения. В этом случае запись уравнений оказывается громоздкой из-за необходимости учета не только взаимных расстояний между скважинами, но также расстояний между скважинами и воображаемыми источниками и расстояний между этими последними.

Для практических расчетов можно использовать приближенную формулу П.П. Голосова для общего дебита скважин прямолинейной батареи: для нечетного числа скважин 2n+1, где n - любое целое число

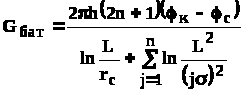
; (4.30)

для четного числа скважин 2n

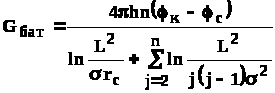
.(4.31)

Здесь h - толщина пласта;  - расстояние между скважинами; L – расстояние до контура.

Ошибка в определении дебитов по данным формулам не превышает 3-4% при L=10км, rс=10см при расстояниях между скважинами 100м  500м.

Приведенные формулы можно использовать при любом контуре питания, т.к. проведенные ранее исследования взаимодействия двух скважин показали, что форма контура питания пласта мало влияет на взаимодействие скважин. Что касается расстояния скважин до контура питания, то по мере приближения скважин к контуру питания эффект взаимодействия уменьшается, но в реальных условиях значительного удаления скважин от контура питания погрешность определения расстояния до контура даже в 100% не отражается значительно на эффекте взаимодействия. Для однородных пластов и жидкостей относительные изменения дебитов скважин, вызванные эффектом взаимодействия, не зависят от физико-геологических характеристик пласта и от физических параметров жидкости.

Рассмотрим теперь фильтрационное поле (рис. 4.10), поддерживаемое, для простоты, бесконечной цепочкой равностоящих скважин (требование бесконечности приводит к ликвидации граничных эффектов на концах батареи и равнодебитности скважин, т.к. все скважины оказываются в равных условиях притока к ним флюидов).

Для получения формул дебита скважины бесконечной прямолинейной батареи использует формулу (4.25) дебита скважины кольцевой батареи. Положим, что

rк=l+a;

a=n /(2 ), (4.32)

где L=const - разность между радиусом контура питания и радиусом кольцевой батареи а; =const - длина дуги окружности радиусом а между двумя соседними скважинами кольцевой батареи.

Подставив значения rк , a в формулу (4.25), получим

,(4.33)

где

z= / (2l).

Переходя в данной формуле к пределу при n и учитывая, что

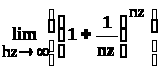=e,

получим формулу массового дебита скважины прямолинейной батареи

. (4.34)

Здесь L - расстояние от контура питания до батареи; - расстояние между скважинами батареи; h - толщина пласта.

Суммарный дебит из n - скважин определится следующим выражением

.(4.35)

Для несжимаемой жидкости соотношение (4.35) можно переписать через давление и объёмный дебит

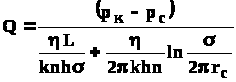. (4.36)

Ортогональная сетка, изображающая фильтрационное поле бесконечной прямолинейной батареи, изображено на рис. 4.11 .

Здесь, как и в кольцевой батарее, имеются главные и нейтральные линии тока, перпендикулярные цепочке. Нейтральными линиями тока вся плоскость течения делится на бесконечное число полос, каждая из которых является полосой влияния одной из скважин, находящейся в середине расстояния между двумя соседними нейтральными линиями. Главные линии тока проходят через центры скважин, параллельно нейтральным линиям.

Изобара, бесчисленное множество раз пересекающая сама себя, отделяет изобары внешнего течения ко всей батареи, охватывающих всю цепочку скважин, от изобар притока к скважине, охватывающих только данную скважину. Точки пересечения граничной изобары являются точками равновесия и они делят интервал между двумя соседними скважинами пополам.

2.1.7 Метод эквивалентных фильтрационных сопротивлений

Данный метод называется методом Борисова и позволяет сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки - к одиночно работающей скважине и к одиночно работающей батареи. Реализация данного метода достигается введением понятий внутреннего и внешнего фильтрационных сопротивлений, которые придают простейший физический смысл членам уравнений, используемых для подсчетов дебитов и значений потенциальных функций. Для выяснения этих понятий сравним формулы (4.35) или (4.36) с законом Ома I=U / R, где I - ток, U - разность потенциалов и R - сопротивление. Из сравнения видно, что фильтрационное сопротивление определяется величиной знаменателя правой части (4.35), который состоит из двух слагаемых. Если в (4.35) оставить только первое слагаемое, то оно будет выражать дебит в прямолинейно-параллельном потоке через площадь величиной nh на длине L . Т.о. первое слагаемое выражает фильтрационное сопротивление потоку от контура питания к участку прямолинейной бесконечной цепочки, занятому n скважинами, в предположении замены батареи галереей. Борисов назвал эту часть фильтрационного сопротивления - внешним фильтрационным сопротивлением

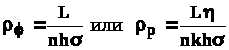.(4.37)

Оставим теперь в (4.35) только второе слагаемое. В этом случае получим аналог формулы Дюпюи для суммарного дебита n скважин при плоскорадиальном течении и в предположении, что каждая скважина окружена контуром питания длиной . Т.о. второе слагаемое выражает местное фильтрационное сопротивление, возникающее при подходе жидкости к скважинам. Появление этого сопротивления объясняется искривлением линий тока у скважин, и по Борисову оно получило название внутреннего

.(4.38)

На внешнее и внутреннее фильтрационные сопротивления разделяется также полное фильтрационное сопротивление кольцевой батареи

.(4.39)

Здесь  выражает фильтрационное сопротивление потоку от контура питания к кольцевой батареи радиуса а в предположении, что поток плоскорадиален и батарея заменена галереей. Внутреннее сопротивление / - это сопротивление плоскорадиального потока от воображаемого контура окружности длиной 2а/n к скважине. Величина 2а/n - длина дуги сектора радиуса а, который содержит одну из скважин батареи.

Электрическая схема в случае одной батареи (рис.4.12) имеет вид (рис.4.13). На рис.4.12 затемнены области внутреннего сопротивления.

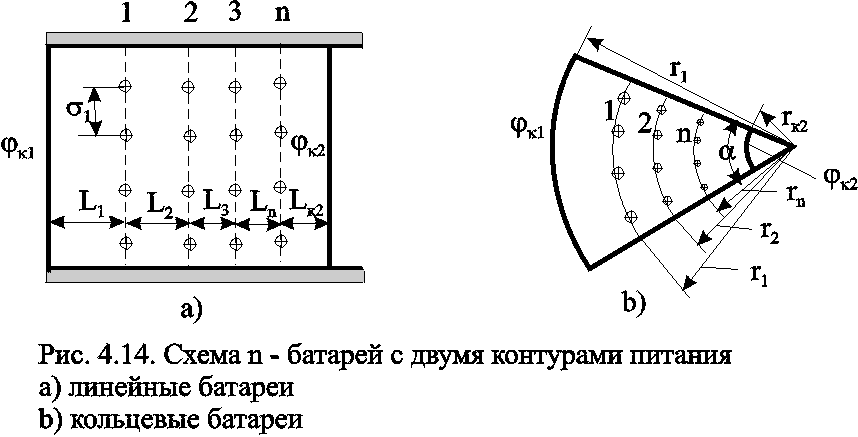
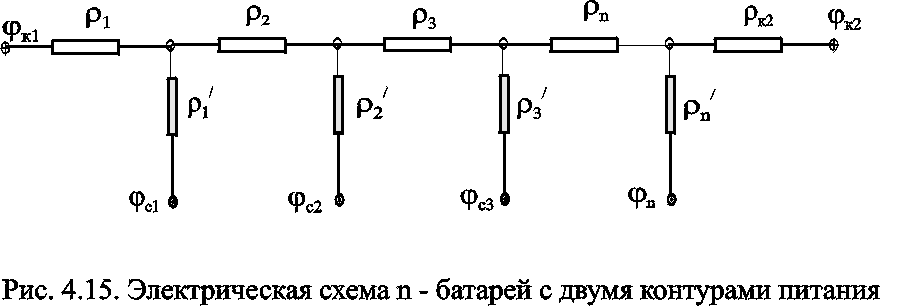
Рассмотрим случай притока к n эксплуатационным и нагнетательным батареям скважин и составим схему сопротивлений. Предположим, что скважины i-ой батареи имеют забойные потенциалы сi (i=1,...,n), пласт имеет контурные потенциалы к1 и к2 (рис. 4.14). Пусть к1 > к2. Очевидно, поток от контура питания к первому ряду скважин будет частично перехватываться первой батареей и частично двигаться ко второй. Поток ко второй батарее будет частично перехватываться второй батареей, частично двигаться к третьей и т.д. Этому движению отвечает разветвленная схема фильтрационных сопротивлений (рис. 4.15).

Расчет ведется от контура с большим потенциалом к контуру с меньшим потенциалом, а сопротивления рассчитываются по зависимостям:

прямолинейная батарея

(4.40)

круговая батарея

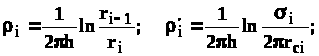(4.41)

где Li - расстояние между батареями (для i=1 - L1=Lк1 ); ri - радиусы батарей (для i=1 - r0=rк ); ki - число скважин в батареи.

Дальнейший расчет ведется, как для электрических разветвленных цепей, согласно законам Ома и Кирхгоффа:

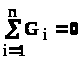- алгебраическая, сумма сходящихся, в узле дебитов равна нулю, если считать подходящие к узлу дебиты положительными и отходящие - отрицательными.

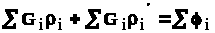
алгебраическая сумма произведения дебитов на сопротивления (включая и внутреннее) равна алгебраической сумме потенциалов, действующих в замкнутом контуре. При этом и дебиты и потенциалы, совпадающие с произвольно выбранным направлением обхода контура, считаются положительными, а направленное навстречу обходу отрицательным.

Следует помнить, что для последовательных сопротивлений =i , а для параллельных

Если одна из границ непроницаема, то расход через неё равен нулю. В этом случае в соответствующем узле схемы фильтрационных сопротивлений задаётся не потенциал, а расход. На рис. 4.16 показана схема в случае непроницаемости второго контура. Вместо потенциала к2, показанного на рис.4.15, здесь в узле задано условие Gi=0.

Приведенные формулы тем точнее, чем больше расстояние между батареями по сравнению с половиной расстояния между скважинами. Если расстояние между скважинами много больше расстояния между батареями, то расчет надо вести по общим формулам интерференции скважин или использовать другие виды схематизации течения, например, заменить две близко расположенные соседние батареи скважин с редкими расстояниями между скважинами (рис. 4.17а) эквивалентной одной батареей - с суммарным числом скважин и проведенной посредине (рис.4.17b).

Вывод

В данной курсовой работе мы выведи дифференциальное уравнение движения сжимаемой и несжимаемой жидкости в пористой среде, то есть уравнение Лапласа. А так же рассмотрели плоские задачи теории фильтрации об установившемся притоке к скважине, такие как приток к совершенной скважине, фильтрационный поток от нагнетательной скважины к эксплуатационной, приток к группе скважин с удаленным контуром питания, приток к скважине в пласте с прямолинейным контуром питания, приток к скважине, расположенной вблизи непроницаемой прямолинейной границы, приток к скважине в пласте с произвольным контуром питания, приток к бесконечным цепочкам и кольцевым батареям скважин, приток к скважинам кольцевой батареи, приток к прямолинейной батареи скважин, метод эквивалентных фильтрационных сопротивлении.

Литература

1. Басниев В.С. и др. Подземная гидравлика. // М.:Недра,1986.-300с.

2. Евдокимова В.А., Кочина И.Н. Сборник задач по пдземной гидравлике. // М.:Недра.-166с.

3.Пыхачев Г.Б., Исаев Р.Г. Подземная гидравлика. //М:Недра,1973.- 359с.

4. Чарный И.А. Подземная гидрогазодинамика. // М. Изд.-во. Нефтяной и горно-топливной лит-ры.- 396с.

5. Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. // М. Недра, 1984.- 211с.

1