Анализ функции фильтрационного сопротивления для неустановившегося притока жидкости (газа) к несовершенной скважине

Министерство общего и профессионального образования РФ

Тюменский Государственный Нефтегазовый Университет

Кафедра РЭНиГМ

Реферат

«Анализ функции фильтрационного сопротивления для неустановившегося притока жидкости (газа) к несовершенной скважине»

Выполнил студент

Группы НГР-96-1

Принял профессор

Телков А. П.

Тюмень 1999 г.

Рассмотрим функция (F) которая есть функ­ция пяти параметров F=F (f_>0>, r_>c>, h, x, t*), каждый из которых — безразмерная ве­личина, соответственно равная

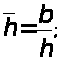
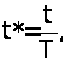_>> _> > _> > _> > (1)

где r — радиус наблюдения;

x — коэффициент пьезопроводности;

Т — полное время наблюдения;

h — мощность пласта;

b — мощность вскрытого пласта;

z — координата;

t — текущее время.

Названная функция может быть ис­пользована для определения понижения (повышения) давления на забое скважи­ны после ее пуска (остановки), а также для анализа распределения потенциала (давления) в пласте во время работы скважины.

Уравнение, описывающее изменение давления на забое, т. е. при x=h; r=r_>c> или r=r_>c>, имеет вид

_> > (2)

где безразмерное значение депрессии связано с размерным следующим соот­ношением

_>> где_>> (3)

здесь Q — дебит;

m — коэффициент вязкости;

k — коэффициент проницаемости.

Аналитическое выражение F для оп­ределения изменения давления на за­бое скважины запишем в виде

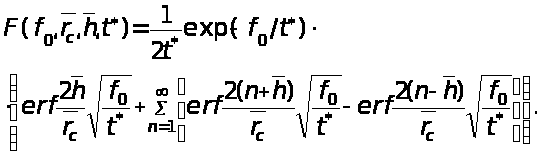_>> (4)

Уравнение (2) в приведенном виде не может использоваться для решения инженерных задач по следующим при­чинам: во-первых, функция (4) сложна и требует табулирования; во-вторых, вид функции исключает возможность выделить время в качестве слагаемого и свести решение уравнения (2) к урав­нению прямой для интерпретации кри­вых восстановления (понижения) давле­ния в скважинах традиционными мето­дами. Чтобы избежать этого, можно по­ступить следующим образом.

В нефтепромысловом деле при гид­родинамических исследованиях скважин широко используется интегрально-пока­зательная функция. Несовершенство по степени вскрытия пласта в этом случае учитывается введением дополнительных фильтрационных сопротивлений (C_>1>), взятых из решения задач для установившегося притока. В соответствии с этим уравнение притока записывается в виде

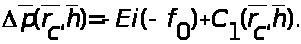_>> (5)

Как видно, дополнительные фильтрационные сопротивления являются функ­цией геометрии пласта. Насколько вер­но допущение о возможности использо­вания значений C_>1>(r_>с>, h), пока еще ни теоретически, ни экспериментально не доказано.

Для неустановившегося притока урав­нение (2) запишем аналогично в виде двух слагаемых, где в отличие от вы­ражения (5) значения фильтрационных сопротивлений являются функцией трех параметров (r_>с>, h, f_>0>)

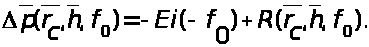_>> (6)

Как _ видим, дополнительное слагае­мое R(r_>c> , h, f_>0>) в уравнении (6) зависит не только от геометрии пласта, но и от параметра Фурье (f_>0>). В дальнейшем бу­дем называть это слагаемое функцией фильтрационного сопротивления. Заме­тим, что при h=l (скважина совершен­ная по степени вскрытия) уравнение (2) представляет собой интегрально-по­казательную функцию

_>> (7)

С учетом равенства (7) решение (6) за­пишем в виде

_>> (8)

Разрешая уравнение (8) относительно функции сопротивления и учитывая уравнение (2), находим

_>> (9)

и на основании равенства (7) приведем выражение (9) к виду

_>> (10)

Численное значение R(r_>с>,h,fo) рас­считано по уравнению (10) на ЭВМ в широком диапазоне изменения парамет­ров r_>c>, h, f_>0>. Интеграл (2) вычислялся методом Гаусса, оценка его сходимости выполнена согласно работе [3]. С уче­том равенства (7) вычисления дополнительно проконтролированы по значени­ям интегрально-показательной функции.

С целью выяснения поведения депрессии и функции сопротивления проана­лизируем их зависимость от значений безразмерных параметров.

1. Определим поведение Dр в зави­симости от значений параметров r_>с>, h, f_>0>.

Результаты расчетов значений де­прессии для каждого фиксированного r_>c> сведены в таблицы, каждая из кото­рых представляет собой матрицу разме­ром 10х15. Элементы матрицы это зна­чения депрессии Dp(r_>c>) для фиксиро­ванных h и f_>0>. Матрица построена та­ким образом, что каждый ее столбец есть численное значение депрессии в зависимости от h, .а каждая строка со­ответствует численному значению де­прессии в зависимости от fo (табл. 1). Таким образом, осуществлен переход от значений безразмерной депрессии Dp(r_>c>, h, f_>0>) к относительной депрессии

Dр*_>i,j> (r_>c>).

Для удобства построения и иллюст­рации графических зависимостей выпол­нена нормировка матрицы. С этой це­лью каждый элемент i-й строки матри­цы поделен на максимальное значение депрессии в данной строке, что соответ­ствует значению j==15. Тогда элементы новой матрицы определятся выраже­нием

_>> (11)

Условимся элементы матрицы назы­вать значениями относительной депрес­сии. На рис. 1 приведен график изме­нения относительной депрессии при фик­сированных значениях h. Характер по­ведения относительной депрессии поз­воляет описать графики уравнением пучка прямых

_>> (12)

Рис. 1. Поведение относительной депрес­сии (r_>c>=0,0200, h_>i>=const, f_>0>) при значениях h, равных: 1— 0,1; 2 — 0,3; 3—0,5; 4 — 0.7; 5 —0,9; 6—1,0.

где k_>i> — угловой коэффициент прямой, который определяется h и от индекса j не зависит.

Анализ зависимости поведения де­прессии Dp^*_>i,j> от f_>0> для всех r_>c> >0,01 показывает, что графики этой зависимости можно описать уравнением пучка прямых для любого значения h. Для r_>c>< 0,01 в графиках зависимости появляются начальные нелинейные уча­стки, переходящие при дальнейшем уменьшении параметра f_>0> (или же при увеличении его обратной величины 1/f_>oj>) в прямые для всех значений h<l,0

(рис. 2). При h=l,0 поведение депрес­сии строго линейно. Кроме того, протя­женность нелинейного участка для раз­ных r_>c> при h=const различна. И чем меньше значение безразмерного ради­уса r_>c> , тем больше протяженность не­линейного участка (рис. 2).

2. Определим поведение R(r_>c>, h, f_>0>) и ее зависимость от безразмерных па­раметров r_>c>, h, f_>0>.

Значения R(r_>c>, h, f_>0>) рассчитаны для тех же величин параметров r_>c>, h, f_>0>. ко­торые указаны в пункте 1, обработка результатов также аналогична. Переход от безразмерной функции сопротивле­ния R(r_>c>, h, f_>0>) к относительной R^*_>i,j> (r_>c>) осуществлен согласно выражению

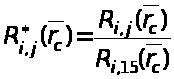_>>. (13)

Анализ поведения R^*_>i,j> (r_>c>) и резуль­таты обработки расчетного материала, где установлена ее зависимость от па­раметров r_>c>, h, f_>0>, частично приведены на рис, 2 (кривые даны пунктиром).

При г_>c> >0,01 для любого h_>i> R^*_>i,j> (r_>c>) уже не зависит от f_>0i> .

Из анализа данных расчета и графи­ков рис. 2 следует: при r_>c><0,01 в по­ведении R^*_>i,j> (r_>c>) для всех h<l,0 на­блюдается нелинейный участок, перехо­дящий с некоторого значения f_>0> (точка С на графике) в прямую линию, парал­лельную оси абсцисс. Важно отметить,

что для одного и того же значения r_>c> абсцисса точки перехода нелинейного участка в линейный для R^*_>i,j> (r_>c>) имеет то же самое значение, что и абсцисса точек перехода для графиков зависи­мости Dp^*_>i,j> (r_>c>) от ln(l/f_>0i> ) (линия CD). Начиная с этого момента, R^*_>i,j> (r_>c>) для данного r_>c> при дальнейшем наблюдении зависит не от времени, а только от h_>i> • И чем выше степень вскрытия, т. е. чем совершеннее скважина,. тем меньше бу­дет значение R^*_>i,j> (r_>c>) И при h=l (сква­жина совершенная по степени вскры­тия) функция сопротивления равна ну­лю. Очевидно, нелинейность Dp^*_>i,j> (r_>c>) связана с характером поведения функ­ции сопротивления, которая, в свою оче­редь, зависит от параметра Фурье. От­метим также, что в точке С (рис. 2) численное значение функции сопротив­ления становится равным значению фильтрационных сопротивлений (C_>1>(r_>c>, h)) для притока установившегося ре­жима.

Рис. 2. Поведение относительной депрес­сии и относительной функции фильтрационного сопротивления (r_>c>=0,0014, h=const, f_>0>) при h, равных: 1,1'—0,1; 2,2'— 0,3; 3,3'—0,5; 4,4'—0,7; 5,5'— 0,9; 6,6'— 1,0.

выводы

1. Депрессия на забое несовершенной по степени вскрытия скважины для всех r_>c> < 0,01 имеет два явно выражен­ных закона изменения: а) нелинейный, который обусловлен зависимостью функ­ции сопротивления от времени и соот­ветствует неустановившемуся притоку сжимаемой жидкости (газа); б) линей­ный, который соответствует квазиустановившемуся притоку и не связан с функцией сопротивления.

2. Величина R(r_>c>, h, f_>0>) для неуста­новившегося притока качественно опи­сывает С_>1>(r_>c>, h) для установившегося, и ее численное значение при любом вскры­тии пласта всегда меньше численного значения С_>1>(r_>c>, h) при установившемся притоке.

3. Полученное аналитическое реше­ние для неустановившегося притока сжимаемой жидкости (газа) к несовер­шенной скважине в бесконечном по про­тяженности пласте преобразовано в прямолинейную анаморфозу, которая позволяет эффективно интерпретировать кривые восстановления забойного дав­ления.

4. Выбор fo, дающего значения Dp^*_>i,j>(r_>c>)=1, не влияет на протяжен­ность нелинейного участка, соответст­вующего неустановившемуся движению, на графики зависимости Dp^*_>i,j>(r_>c>) от ln(1/f_>0i>).

ЛИТЕРАТУРА

1. Т е л к о в В. А. Приток к точечному стоку в пространстве и к линии стоков в полу бесконечном пласте. НТС. Вып. 30, Уфа, 1975.

2. Л е о н о в В. И„ Телков В. А., Каптелинин Н. Д. Сведение задачи неустановившегося притока сжимаемой жидкости (газа) к несовершенной скважи­не к решению уравнения пьезопроводности. Тезисы докладов на XIII научно-техниче­ском семинаре по гидродинамическим ме­тодам исследований и контролю процессов разработки нефтяных месторождений. Пол­тава, 1976.

3. Б а х в а л о в Н. С. Численные мето­ды. Изд-во «Наука», М., 1974.