Проектирование и расчет обделки гидротехнических туннелей

Проектирование и расчет обделки гидротехнических туннелей

Пояснительная записка к курсовой работе

Студент Гиргидов А.А., Группа : 5011/1

Санкт-Петербургский Государственный технический университет

Кафедра подземных сооружений, оснований и фундаментов

2000

Исходные данные

Режим работы – безнапорный.

Класс капитальности – II.

Максимальный расход воды в туннеле – м3/с.

Средняя скорость протекания воды в туннеле – м/с.

Отметка верха лотка туннеля – м/с.

Структурно-геологическая характеристика горных пород приведена в таблице:

Номер

пласта

Наименование

горной породы

Отметка

кровли

пласта, м

1

Суглинок

0

2

Сланец

-40

Физико-механические характеристики горных пород:

Номер

Пластов

Удельный вес сухого грунта

Влажность

Коэффициенты

Поперечной деформации

удельного отпора

крепости

1

2.04

2

2.41

0.04

58

2.3

0.26

290

3.5

Определение внутренних размеров туннеля.

Будем считать, что колебания воды в туннеле не превышают , где - высота туннеля. Тогда отношение

,

где - ширина туннеля по дну.

Принимаем

,

где - радиус сечения туннеля, который определяется по формуле:

,

где м3/с - максимальный расход воды в туннеле; м/с - средняя скорость протекания воды в туннеле;

м.

Согласно таблице 2 [1, стр.17], получаем следующие соотношения основных размеров:

м;

.

Выбор формы сечения туннеля

Выбор формы поперечного сечения туннеля осуществляется с учетом условий статической работы обделки, гидравлических условий пропуска воды, а также способов и условий производства работ при сооружении туннеля.

В нашем случае туннель работает в безнапорном режиме, поэтому определяющей нагрузкой при выборе формы сечения является горное давление, величина и направление которого может оцениваться коэффициентом крепости породы , окружающей туннель.

Согласно таблице 1. [1, стр.14] поперечное сечение туннеля принимается корытообразную форму (II форма).

Составление эскиза конструкции обделки и выбор материалов для ее возведения.

Принимаем корытообразную монолитную железобетонную обделку (рис.4.1). Согласно таблице 3 [1, стр.23], толщина обделки назначается по следующим зависимостям:

м;

;

м;

м.

Обделка выполняется из железобетона, для этого используется бетон марки М 200 и арматура класса А II.

Определение нормативных и расчетных нагрузок, их сочетаний и коэффициентов упругого отпора породы

Одной из основных нагрузок, действующих на обделку туннеля, является горное давление. Это давление возникает из-за того, что при устройстве туннеля в горных породах образуется свод обрушения – область грунта, теряющего равновесие и, вследствие этого, оказывающего давление на обделку. Распределение нагрузок на обделку туннеля и форма свода обрушения приведена на рис.4.

Величина горного давления определяется расчетом, основанном на использовании значений характеристик пород, окружающих туннель. При этом в соответствии с указаниями СН распределение вертикального и горизонтального горных давлений принимаются равномерными по пролету и высоте выработки :

м;

м.

Вертикальное горное давление определяется по формуле:

,

где - коэффициент, равный при м; - удельный вес грунта т/м3;

Высота свода обрушения , определяется по формуле:

,

где - пролет свода обрушения:

м,

где - расчетный угол внутреннего трения породы;

.

Таким образом, получается, что

тс/м.

Горизонтальное нормативное горное давление определяется по формуле:

тс/м.

Возможность возникновения давления на обделку снизу (дутье) проверяется по условию:

,

где тс/м2 - сцепление породы по подошве выработки;

тс/м;

.

Следовательно,

тс/м,

следовательно, дутья нет.

Так как давление на обделку снизу отсутствует, принимается разомкнутая конструкция обделки.

Определение расчетного коэффициента отпора :

по боковой поверхности

,

где кгс/см3 - коэффициент удельного отпора, м;

тс/м3;

по подошве стены

,

где - коэффициент поперечной деформации породы,

тс/м3.

Для статического расчета обделки, который будет выполнен далее, выделим на срединной линии обделки 12 точек и определим их положение в системе координат, положение которой показано на рисунке 3. Для каждой точки определим координаты х и у, а также толщину обделки. Полученные результаты представим в виде таблицы и туда же запишем значения коэффициентов отпора К .

Таблица 5.1.

№

х, м

у, м

h, м

К, тс/м3

1

0.00

0.00

0.2875

109434

2

0.64

0.18

0.2887

109434

3

1.21

0.35

0.2924

109434

4

1.75

0.75

0.2988

109434

5

2.15

1.19

0.3086

109434

6

2.41

1.80

0.3227

109434

7

2.47

2.46

0.3450

109434

8

2.47

3.02

0.3450

109434

9

2.47

3.77

0.3450

109434

10

2.47

4.52

0.3450

109434

11

2.43

5.02

0.3450

635775

Статический расчет монолитной обделки туннеля

6.1Краткое описание метода метрогипротранса

Обделка туннеля, имеющая произвольную форму и окруженная упругой средой является бесконечное число раз статически неопределимой системой, точное определение усилий и реакций в которой невозможно в настоящее время. Для определения внутренних усилий в обделке используют численные методы дающие приближенное решение. Одним из наиболее точных методов является метод метрогипротранса, основанный на преобразовании заданной системы в расчетную принятием следующих допущений:

криволинейное очертание обделки заменяется вписанным многоугольником (рис.5);

непрерывное изменение жесткости обделки заменяется ступенчатым и постоянным в пределах каждой стороны многоугольника;

распределенные нагрузки заменяют усилиями сосредоточенными в вершинах многоугольника;

сплошную упругую среду заменяют отдельными упругими опорами расположенными перпендикулярно к поверхности обделки и помещенными в вершинах многоугольника.

Угол характеризует зону безотпорного участка, которая устанавливается расчетом. Если при расчете реакций опор, поместить опоры в сектор, охватываемый углом , то их реакции получаются отрицательными. Это соответствует отрыванию обделки от породы и имеет физический смысл только в случае анкеровки обделки в окружающую породу. Т.к. в нашем проекте этот вариант не рассматривается, то опоры, попавшие в этот сектор исключаются из рассмотрения, а реакции в них принимаются равными нулю (см. распечатку).

Основная система и канонические уравнения

Основная система представляет собой шарнирную цепь (шарниры в местах упругих опор и замке).

Расчет ведется методом сил, т.к. он дает минимальное число неизвестных. За лишние неизвестные принимаются парные моменты в шарнирах, которые определяются решением системы канонических уравнений, каждое из которых исключает взаимный поворот стержней сходящихся в шарнире.

Канонические уравнения записываются в следующем виде:

(6.1)

где - число узлов на полупериметре срединной линии обделки; и -угловые перемещения в точке по направлению неизвестного момента от действия парных единичных моментов, приложенных в точке и от внешних нагрузок ; - угол поворота пяты стены обделки от действия единичного момента в пяте, равный

,

где тс/м3– коэффициент упругого отпора пяты,

- момент инерции сечения пяты.

Угловые перемещения определяются по формулам строительной механики:

; (6.2)

где - изгибающие моменты и нормальные силы в основной системе от действия единичных моментов, приложенных в точках i и j; – номер стержня конструкции или опоры; - усилия в опоре в основной системе от действия парных единичных моментов, приложенных в точках i и j; - момент инерции,

площадь сечения и длина стержня ;- характеристика жесткости опоры, определяемая по формуле:

,

где - ширина опоры.

В формуле (6.2.) 1-е слагаемое учитывает влияние изгиба стержней; 2-е слагаемое – продольное сжатие стержней, 3-е слагаемое – влияние осадки упругих опор.

,

где - осадка упругой опоры под действием единичной силы; коэффициент отпора породы на опоре ; - напряжение породы под опорой от действия единичной силы.

Основная система представлена на рисунке 6.

Для определения грузовых перемещений , усилия заменяем усилиями в основной системе от действия нагрузок.

Рассмотрим метод построения эпюр М>р> и N>р> на примере узлов 1 и 2 (рис.7).

Дано: Р>1>, Р>2>, Е>1>, Е>2> – внешняя нагрузка; V>1>>p>, H>1>>p> – реакции в шарнире от внешней нагрузки; х>1>, у>1>, х>2>, у>2> координаты узлов.

Требуется найти реакцию опоры от действия внешней нагрузки R>1>>p>.

Для этого запишем уравнения моментов и приравняем их к нулю. Решая уравнения определим R>1>>p> и R>2>>p>. Проверкой может служить условие равенства нулю суммы проекции всех сил на ось ОХ.

Аналогично определяется R>ip>.

Ту часть обделки, где наблюдается зона безотпорного участка, будем рассчитывать как трехшарнирную арку. По заданным значениям нагрузок Р и Е, и координатам вершин углов можно найти реакции в шарнире V>1р>, Н>1р> и построить эпюру моментов на участке обделки 0 - 1.

Эпюра моментов М>р> в арке, изображенной на рис.6 будет ненулевой. На участке обделки 1 - n значения моментов от действия основной нагрузки в основной системе равны нулю.

Для определения значений >ij> коэффициентов требуется построить эпюры от действия единичных моментов в узлах 0 - n в основной системе. Метод расчета остается тем же, что использовался при построении эпюры М>р>, а именно:

рассматривается трехшарнирная арка, нагрузки Е и Р приравниваются к нулю, т.к. в методе сил основные нагрузки при построении эпюр моментов во вспомогательных состояниях не рассматриваются; в узле 0 прикладывается единичный момент М>0 >= 1 (см. рис.8 ), строится эпюра моментов в арке, а также определяются значения реакций в шарнире V>10> и H>10>;

полагая внешние нагрузки равными нулю, используя метод изложенный выше, построим эпюры М>0>, N>0> и R>0> (расчетная схема показана на рис.8);

прикладывая к основной системе в качестве внешней нагрузки момент М>1> = 1, строим эпюры М>1>, R>1>, N>1>.

Аналогично строятся эпюры для остальных вспомогательных состояний.

Методом Верещагина вычисляем значения коэффициентов >ij>, >i> и, подставляя их в систему канонических уравнений, находим значения моментов в вершинах углов многоугольника, аппроксимирующего обделку.

Затем строим эпюры М, N и R для зоны безотпорного участка, определяя значения расчетных величин в вершинах углов по следующим формулам:

где m – номер точки, для которой определяем значения М, N, и R; М>mp>, N>mp>, и R>mp> – усилия в точке m основной системы в грузовом состоянии; М>m>>к>, N>m>>к> и R>m>>к> – усилия в точке m основной системы в к-том вспомогательном состоянии; М>к> – момент в точке к расчетной схемы.

Выбор арматуры

В данном пункте определяется необходимая площадь сечения арматуры в обделке. Для этого предварительно намечается три сечения, в которых значения момента экстремальны, и рассматриваются последовательно - в строительный и эксплуатационный периоды. Расчет ведем по первой группе предельных состояний по методу, изложенному в [3, стр. 137]

Сечение I-I (строительный период).

тс*м – изигбающий момент;

тс – нормальная сила;

м – толщина обделки;

м – эксцентриситет;

h>об>/6= 0.29/6=0.048м;

е>0><h>0б >/6;

h>о>= h>об> - а = 0.29 – 0.05=0.24 м – полезная толщина обделки;

R>пр>=900 тс/м2 – призменная прочность бетона;

R>а>=2100 тс/м2 – расчетная прочность арматуры;

k>н>=1,2;

F>а>= 0.

тс*м.

,

Следовательно,

;

м;

см2.

Сечение I-I (эксплуатационный период).

Аналогично:

тс*м – изигбающий момент;

тс – нормальная сила;

м – толщина обделки;

м – эксцентриситет;

В следствие того, что исходные величины равны аналогичным величинам строительного случая, то расчет не приволдится.

Определим площадь сечения арматуры из условия минимального армирования. Минимальная степень армирования

;

.

Т.о.,

см2,

см2,

Сечение II-II (строительный период).

тс*м – изигбающий момент;

тс – нормальная сила;

м – толщина обделки;

м – эксцентриситет;

h>об>/6= 0.31/6=0.052м;

е>0><h>0б >/6;

h>о>= h>об> - а = 0.31 – 0.05=0.26 м – полезная толщина обделки;

R>пр>=900 тс/м2 – призменная прочность бетона;

R>а>=2100 тс/м2 – расчетная прочность арматуры;

k>н>=1,2;

F>а>= 0.

тс*м.

,

Следовательно,

;

м;

см2.

Сечение II-II (эксплуатационный период).

Аналогично:

тс*м – изигбающий момент;

тс – нормальная сила;

м – толщина обделки;

м – эксцентриситет;

В следствие того, что исходные величины равны аналогичным величинам строительного случая, то расчет не приволдится.

Определим площадь сечения арматуры из условия минимального армирования. Минимальная степень армирования

;

.

Т.о.,

см2,

см2,

Учитывая тот факт, что значение момента M в сечении III-III значительно меньше, чем в сечении II-II, делается вывод, что в сечении III-III определяющим является

Cечение III-III:

.

Окончательно принимаем арматуру:

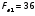см2 5 30 мм;

см2 10 26 мм;

см2 5 12 мм.

Список литературы

Васильев И.М. Расчет монолитных обделок гидротехнических туннелей. – Л.: ЛПИ, 1980.

Автоматизированный расчет усилий в обделках гидротехнических туннелей. Методические указания. – Л.: ЛПИ, 1983.

Руководство по проектированию гидротехнических туннелей. Гидропроект им. С.Я. Жука. – М. Стройиздат, 1982.