Основные положения прочностной теории напряженного состояния
Основные положения прочностной теории напряженного состояния
Ельцов Ю.А.
Ижевский государственный технический университет
Статья посвящена теоретическому определению нормальных и касательных напряжений в грунтах. В статье даются основные предпосылки расчета. В известные теории прочности вносятся поправки, которые с точки зрения автора дают более объективные результаты расчетов, подтверждаемые экспериментальными замерами.
В известных теориях прочности исходят из следующих основополагающих гипотез: сплошности среды и равенства нулю начальных (внутренних) напряжений. Исключение внутренних напряжений из рассмотрения не дает полного представления о действительном напряженном состоянии и динамике его развития.
Исходное (начальное) напряженное состояние - это система природных (естественных) внутренне уравновешенных напряжений в твердом теле (среде).
Напряженно-дислоцируемое (возбужденное) состояние, созданное сложением внешних силовых воздействий и внутренних напряжений от температурных, химических и силовых факторов.
Измененное (остаточное) напряженное состояние, возникшее после исключения или ослабления силового воздействия (разгрузки).
Приобретенное (остаточное) напряженное состояние, сформированное под влиянием геохимических, геостатических и геодинамических релаксационных процессов.
Теория прочности Кулона-Мора, характеризующая условия предельного напряженного состояния исходя из принятых геометрических построений, в настоящее время подвергается существенной критике, т.к. устанавливает сложный характер зависимости компонент напряжений от параметров прочности.
В прочностной теории напряжений основным условием является получение простых прямолинейных зависимостей, согласующихся с экспериментальными. Это достигается новыми приемами геометрических построений предельной линии сдвига и кругов напряжений.
При сложном напряженном состоянии
( )
построение кругов напряжений и предельной
линии сдвига ведется по схеме рис. 1.Б.,
когда значения
)
построение кругов напряжений и предельной
линии сдвига ведется по схеме рис. 1.Б.,
когда значения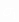 ,
откладываются от конца отрезка
,
откладываются от конца отрезка ,
равного полусумме поперечных напряжений
,
равного полусумме поперечных напряжений
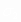 и
и
 с
поправкой на отклонение центра на угол
φ, тогда
с
поправкой на отклонение центра на угол
φ, тогда
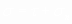
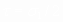 ;
(1)
;
(1)
где .
.
В этом случае предельная линия
сдвига, секущая круги напряжений, в
точках с τmax, будет прямой в пределах
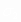 ≤
≤
 (одноосного
сжатия). Уравнение этой прямой, при
подстановке
(одноосного
сжатия). Уравнение этой прямой, при
подстановке
 и
и
 из
(I) в формулу Кулона
из
(I) в формулу Кулона
> >(2)
>(2)
будет иметь вид:
 ,
(3)
,
(3)
где tg φ - модуль трения; с v сцепление связности, характеризующее начальное трение скольжение.
В условиях осевой симметрии ( )
уравнения (1) приобретают вид:
)
уравнения (1) приобретают вид:
 ,
,
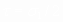 .
(4)
.
(4)
Отсюда уравнение предельной линии сдвига запишется:
 .
(5)
.
(5)
При одноосном сжатии имеем:
 .
(6)
.
(6)
При режиме преодоления "упругих" связей, при одноосном сжатии,
 (7)
(7)
а при сложном напряженном
состоянии, где
 режим
преодоления структурных связей будет
происходить когда:
режим
преодоления структурных связей будет
происходить когда:
 (8)
(8)
Внутренне уравновешенное
напряженное состояние (остаточные
напряжения), в условиях
 характеризуется
напряжениями откладываемыми на отрезке
"давление связности" (БО по схеме
рис.1.Б.)
характеризуется
напряжениями откладываемыми на отрезке
"давление связности" (БО по схеме
рис.1.Б.)
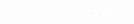
 (9)
(9)
Растяжение реализуется на
преодоление сил связности и ведет к
ослаблению сцепления связности.
Растягивающее напряжение
 откладывается
по отрицательному направлению оси
откладывается
по отрицательному направлению оси ,
с возможным переносом на ось
,
с возможным переносом на ось
 (см.
схему рис.1 .А.). Согласно принятому
построению
(см.
схему рис.1 .А.). Согласно принятому
построению
 .
(10)
.
(10)
или
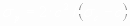 .
.
Произведено уточнение исходных
условий осевого растяжения
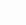 трубчатых
образцов, находящихся под внутренним
давлением
трубчатых
образцов, находящихся под внутренним
давлением :
:
 ,
(11)
,
(11)
 ,
,
где ,
,
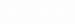 см.
(1), здесь знак
см.
(1), здесь знак
минус опущен при использовании
отрицательного направления оси
 для
удобства написания и расчетов.
для
удобства написания и расчетов.
Тогда уравнение предельной линии растяжения, аналогично (3), будет иметь вид
 .
(12)
.
(12)
где
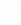 и
и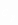 - параметры предельной линии растяжения
в условиях сложного напряженного
состояния, аналогичные сцеплению и углу
внутреннего трения.
- параметры предельной линии растяжения
в условиях сложного напряженного
состояния, аналогичные сцеплению и углу
внутреннего трения.

Рис. 1. Схемы построений кругов напряжений и предельной линии сдвига.
А - в режиме растяжения: Б - при сложном напряженном состоянии.
Выразив внутреннее сопротивление
cp через сопротивление одноосного
растяжения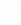 ,
подобно (6), имеем:
,
подобно (6), имеем:
 ,
(13)
,
(13)
откуда
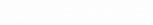 (14)
(14)
Принятые схемы построения предельной линии сдвига и кругов напряжений позволили установить функциональные связи компонент напряжений от параметров прочности с и φ в разных стадиях и режимах напряженного состояния: в исходном, внутренне уравновешенном; при преодолении упругих и предельных сопротивлений от внешних воздействий; в режимах одноосного сжатия и растяжения. Все основные уравнения проверены по результатам испытаний разнородных материалов и показали удовлетворительную для практики степень сходимости по сравнению с известными решениями.
Важным достижением, подкрепленным опытными данными, является положение о том, что касательные напряжения составляют половину от максимальных нормальных напряжений. Известное же их равенство полуразности нормальных напряжений ведет к нелинейности предельной линии сдвига и затрудняет установление связей между рассматриваемыми параметрами напряженного состояния.
Сопоставление различных теорий
|
По условию прочности автора |
По Кулону-Мору-Хиллу |
|
1.
Геометрическое построение предельных
линий сдвига (ПЛС) не менее чем по 2-3
точкам при
|
|
|
1.1. Размеры
1.2.
Координаты точек ПЛС находятся по
формулам: |
1.1. Все размеры
1.2. |
|
2.
Вид ПЛС по экспериментальным значениям
|
|
|
2.1.
Прямая в пределах
|
2.1.
Прямая в пределах
|
|
3.
Геометрическое построение ПЛС не
менее чем по 2-3 точкам при
|
|
|
3.1. Построение при
3.2.
|
3.1. Нет. 3.2. Нет решения. |
|
4.
Вид ПЛС по экспериментальным значениям
|
|
|
4.
1. Прямая в пределах
|
4.1. Нет. |
|
5. Решения и прогнозы |
|
|
5.1. Однозначное определение
прочности (параметров
5.2. Остаточные напряжения
отождествляются с Lдавлением связности¦
5.3. Связь между одноосным сжатием
5.4. Прогнозируется предшествующее давление испытанное материалом и степень его релаксации. 5.5. Напряженное состояние земной коры обусловлено остаточными напряжениями и пригрузкой вышележащих пород.
5.6. Определяемые параметры
прочности
5.7. Однозначное прогнозирование оползневых склонов в состоянии длительной и предельной устойчивости. |
5.1. Угол
5.2. Не устанавливаются. 5.3. Не устанавливается. 5.4. Не устанавливается. 5.5. Отмечается существенное расхождение в значениях касательных напряжений. 5.6. Степень сопоставимости более низкая. 5.7. Вариантное прогнозирование устойчивости. |
Список литературы
Для подготовки данной применялись материалы сети Интернет из общего доступа

 .
.
 ,
, .
.
 и
далее с переломом и уменьшением угла
до
и
далее с переломом и уменьшением угла
до .
.
 с
переломом и выполаживанием при
с
переломом и выполаживанием при
 (τ→const).
(τ→const).
 ,
где
,
где

 и
и .
.