Гидродинамический метод оценки ЭЗ
Гидродинамический метод оценки ЭЗ
Р.С. Штенгелов
Структура фильтрационного сопротивления месторождения:
 ,
,
где
 - гидродинамические Параметры водоносной
системы,
- гидродинамические Параметры водоносной
системы,
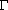 -
Граничные условия потока,
-
Граничные условия потока,
t - расчетное время развития депрессионной воронки,
 -
схема и конструкция Водозаборного
сооружения.
-
схема и конструкция Водозаборного
сооружения.
При применении гидродинамического
метода оценки все эти компоненты,
интегрально образующие величину
 ,
разведуются раздельно, любыми доступными
методами и затем раздельно учитываются
в расчетных формулах фильтрации к
скважинам или вводятся в состав моделей
для моделирования работы водозабора.
,
разведуются раздельно, любыми доступными
методами и затем раздельно учитываются
в расчетных формулах фильтрации к
скважинам или вводятся в состав моделей
для моделирования работы водозабора.
Поясняющие примеры:
По материалам разведки доказана возможность применения расчетной схемы неограниченного в плане, однородного, изолированного в разрезе пласта; следовательно, расчет понижения уровня в водозаборной скважине можно сделать по формуле Тейса:

то есть

Таким образом, можно видеть, что в
условиях "схемы Тейса" величина
 зависит
от гидродинамических параметров
зависит
от гидродинамических параметров
 ,
времени эксплуатации
,
времени эксплуатации
 и характеристики водозабора
и характеристики водозабора
 .
Данные о граничных условиях Г в описании
отсутствуют, что вполне понятно для
неограниченного пласта.
.
Данные о граничных условиях Г в описании
отсутствуют, что вполне понятно для
неограниченного пласта.
Другой пример: водозаборная скважина рассчитывается для условий стационарного режима фильтрации в связи с перетеканием из смежного водоносного горизонта:

где
 - фактор перетекания.
- фактор перетекания.
В этом случае
 ;
в этом описании фактор перетекания
;
в этом описании фактор перетекания
 является "представителем" граничных
условий Г, а время и водоотдача отсутствуют,
так как речь идет о стационарном режиме
фильтрации.
является "представителем" граничных
условий Г, а время и водоотдача отсутствуют,
так как речь идет о стационарном режиме
фильтрации.
Такие примеры можно продолжить. Например,
для несовершенных водозаборных скважин
в величине сопротивления появятся
 -
длина фильтра и расстояние от края
фильтра до кровли пласта (Вз); если
область фильтрации в плане ограничена
(выклинивание пласта, фациальное
замещение...), то появится расстояние до
этой границы
-
длина фильтра и расстояние от края
фильтра до кровли пласта (Вз); если
область фильтрации в плане ограничена
(выклинивание пласта, фациальное
замещение...), то появится расстояние до
этой границы
 (Г). Любое изменение в расчетной схеме
отражается в содержании обобщенного
фильтрационного сопротивления
(Г). Любое изменение в расчетной схеме
отражается в содержании обобщенного
фильтрационного сопротивления
 .
.
Итак, при использовании гидродинамического метода оценки ЭЗ нужно РАЗДЕЛЬНО РАЗВЕДАТЬ И ОЦЕНИТЬ ВСЕ КОМПОНЕНТЫ РАСЧЕТНОЙ СХЕМЫ.
После этого подсчет запасов (точнее, расчет водозабора, т.к. подсчет запасов - это более общая задача) выполняется
- или АНАЛИТИЧЕСКИ (по формулам теории притока к скважинам) - при этом формулы выбираются в соответствии с разведанной расчетной схемой, а "начинкой" формул являются разведанные параметры)
- или с использованием МОДЕЛИРОВАНИЯ работы водозабора - создается модель МПВ, на которой решается прямая задача с целью получить распределение (во времени и пространстве) напоров (или понижений) при полностью известном (разведанном!) распределении параметров, граничных условий и т.д. (известны все аргументы, ищем функцию).
Во всех случаях для выполнения
гидродинамического расчета необходимо
составление ФИЛЬТРАЦИОННОЙ СХЕМЫ
МЕСТОРОЖДЕНИЯ, которая является конечной
целью разведки и должна адекватно, с
наилучшей возможной степенью приближения
отражать все те гидрогеологические
условия, которые в конкретном случае
контролируют величину
 .
.
Основой для составления фильтрационной схемы являются результаты поисково-разведочных работ: они (работы) должны быть запроектированы, проведены и интерпретированы так, чтобы схема стала достоверной, т.е. содержала бы в себе все те элементы природной обстановки, которые в конкретном случае являются ЗНАЧИМЫМИ для формирования балансово-гидродинамической ситуации.
Принципы и содержание фильтрационной схематизации гидрогеологических условий для целей любого гидрогеодинамического расчета уже подробно прорабатывались в курсе "Гидрогеодинамика". Здесь мы кратко их повторим, учитывая некоторую специфику расчетов водозаборных сооружений.
Обязательные разделы фильтрационной схематизации
Вопросы, которые гидрогеолог должен поставить перед собой и обосновать ответ по данным разведки
• Должен быть обоснован ожидаемый РЕЖИМ ФИЛЬТРАЦИИ ВО ВРЕМЕНИ при работе водозабора. Ответ на этот вопрос обосновывается:
- выявленными источниками формирования баланса водоотбора и прогнозируемым временем проявления каждого из них,
- заданным режимом водоотбора (вдруг периодический?)
В зависимости от решения по этому пункту расчетной схематизации прогноз работы водозабора может быть выполнен в стационарном или нестационарном виде - первый вариант проще в исполнении (особенно при моделировании) и требует меньшего числа исходных данных (не нужны емкостные параметры).
Возможность наступления стабилизации
депрессии
 в
простых случаях можно просчитать
аналитически:
в
простых случаях можно просчитать
аналитически:
- например, если водозабор расположен у реки
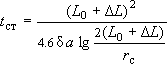 ,
,
где
 -
относительная погрешность (по понижениям)
признания факта стабилизации; например,
при
-
относительная погрешность (по понижениям)
признания факта стабилизации; например,
при
 =
0.1 стабилизация считается наступившей
при
=
0.1 стабилизация считается наступившей
при
 =
9 м, хотя "истинная" стабилизация
наступит позже, при
=
9 м, хотя "истинная" стабилизация
наступит позже, при
 =
10 м.
=
10 м.
- при наличии перетекания

• Должна быть обоснована ожидаемая ПРОСТРАНСТВЕННАЯ СТРУКТУРА ПОТОКА при работе водозабора, определяемая степенью деформации гидродинамической сетки по пространственным координатам. Ее обоснование производится на основе общих гидрогеодинамических предпосылок:
конфигурация границ в плане и их положение в разрезе,
расположение и степень несовершенства водозахватных устройств,
соотношение мощности пласта и его размеров в плане и др.
Возможные варианты расчетной пространственной структуры течения:
трехмерная,
двумерная (в плане или разрезе),
и даже одномерная (обычно радиальная).
Для упрощения расчетов желательно понизить мерность потока (но обоснованно!). Например, можно использовать предпосылку перетекания - при соотношении коэффициентов фильтрации слоев в слоистых разрезах порядка 20-50 и более (напомнить преломление линий тока по правилу тангенсов) можно реальный пространственный поток рассматривать как плоско-пространственный, что легче в расчетном смысле и проще с точки зрения параметрического обеспечения.
• Характер распределения в плане и разрезе необходимых параметров водоносной системы :
проницаемость (проводимость для одномерных и плановых потоков или коэффициент фильтрации для профильных и пространственных потоков)
емкость (водоотдача для моделирования или уровне- пьезопроводность для большинства аналитических решений).
Возможные варианты схематизации выявленного при разведке распределения этих параметров:
а) однородный пласт,
б) квазиоднородный - хаотическое распределение относительно небольших элементов неоднородности с небольшой амплитудой колебания параметра,
в) упорядоченно-неоднородный - при наличии геометрически правильных границ неоднородности (прямая линия, круг, полоса и т.п.) или при наличии функциональной, генетически обусловленной зависимости параметра от природных факторов (мощности пласта, глубины эрозионного вреза и т.п.),
г) существенно-неоднородный - неупорядоченно расположенные крупные элементы неоднородности с контрастными различиями параметра.
Для неоднородных пластов составляются карты параметров с использованием изолиний или по кусочно-неоднородному принципу ("лоскутное одеяло").
Проще для расчетов однородные схемы. При неоднородности, как правило, приходится применять моделирование, так как формулы становятся слишком громоздкими или отсутствуют вовсе.
Важная деталь: по мере удаления от водозабора роль неоднородности (т.е. степень ее влияния на результат расчета - понижения в водозаборе) уменьшается. С максимальной точностью нужно учитывать неоднородность
в районе расположения водозахватных устройств
на участках между водозабором и важными границами; для остальной площади обычно можно использовать осредненные значения.
Полезная, но пока слабо разработанная методически вещь: применение так называемых разведочных расчетов (В.М.Шестаков), факторно-диапазонного анализа (И.К.Гавич); суть их заключается в экспериментальной (обычно на модели) оценке влияния того или иного элемента фильтрационной схемы на конечный результат прогнозного расчета.
• ГРАНИЧНЫЕ УСЛОВИЯ потока в плане и в разрезе (ГУ). Они должны быть определены для области ожидаемой воронки депрессии. Но существует и обратная связь - размер воронки, в свою очередь, зависит от характера и положения граничных условий, поэтому вопрос о необходимых размерах области решения прогнозной задачи приходится решать путем последовательных приближений.
ГУ могут быть внешними и внутренними; внешние должны быть определены в любом случае, внутренние - если они имеются.
Для каждого граничного элемента необходимо обосновать:
пространственное положение и форму граничного условия (точка, линия, поверхность),
гидродинамический род условия,
количественные показатели условия (для каждого рода - свой набор).
Возможные варианты РОДА ГРАНИЧНЫХ УСЛОВИЙ: обычно говорят о трех родах граничных условий, хотя можно обойтись и двумя.
Математическое описание граничных условий делаем (для простоты) в удельной форме, т.е. на единицу (длины, площади) граничного элемента.
= Граничное условие 2 рода - ЗАДАННОЙ
ЯВЛЯЕТСЯ ФУНКЦИЯ РАСХОДА ЧЕРЕЗ ГРАНИЦУ:
 ;
здесь ГК - набор координат граничного
элемента, т.е.
;
здесь ГК - набор координат граничного
элемента, т.е.
 в зависимости от мерности потока и
границы.
в зависимости от мерности потока и
границы.
Что значит "является заданной"?
Это значит, что функциональное описание величины трансграничного расхода известно заранее на весь период прогноза и не зависит от изменений, происходящих в области под влиянием водозабора в прогнозный период. Напор на границе 2 рода на прогноз неизвестен и вычисляется как результат решения.
Пример: поток, приходящий в расчетную
область из удаленных областей питания
("боковой приток"); его величина не
зависит ни от каких изменений напора
 в расчетной области, т.е. не реагирует
на работу водозабора.
в расчетной области, т.е. не реагирует
на работу водозабора.
Частные случаи ГУ 2 рода:
- - расход через границу не зависит от
времени, но может быть разным на разных
участках границы;
- расход через границу не зависит от
времени, но может быть разным на разных
участках границы;
- - расход через границу не зависит от
времени и одинаковый для всей границы;
- расход через границу не зависит от
времени и одинаковый для всей границы;
- - непроницаемая граница.
- непроницаемая граница.
= Граничное условие 3 рода - ЗАДАННЫМ ЯВЛЯЕТСЯ ЛИНЕЙНЫЙ ХАРАКТЕР СВЯЗИ МЕЖДУ РАСХОДОМ ЧЕРЕЗ ГРАНИЦУ И НАПОРОМ В ПЛАСТЕ (точнее - перепадом напоров между пластом и границей).
На такой границе неизвестны ни напор
 в приграничной области пласта, ни
трансграничный расход
в приграничной области пласта, ни
трансграничный расход
 ;
они взаимно регулируют друг друга:
изменение напора (в нашем случае -
понижение от действия водоотбора)
вызывает пропорциональное изменение
расхода, который, в свою очередь, влияет
на положение уровней:
;
они взаимно регулируют друг друга:
изменение напора (в нашем случае -
понижение от действия водоотбора)
вызывает пропорциональное изменение
расхода, который, в свою очередь, влияет
на положение уровней:
 ,
,
при этом (рис.1):
 ,
т.е. напор на границе известен заранее
и не зависит от ситуации в пласте (это
упрощенное описание, но пока будем
рассматривать именно так);
,
т.е. напор на границе известен заранее
и не зависит от ситуации в пласте (это
упрощенное описание, но пока будем
рассматривать именно так);
 -
формально коэффициент пропорциональности
между разностью напоров и расходом
через границу; физически - это фильтрационное
сопротивление границы, т.е. параметр
граничного условия 3 рода. В простом
случае
-
формально коэффициент пропорциональности
между разностью напоров и расходом
через границу; физически - это фильтрационное
сопротивление границы, т.е. параметр
граничного условия 3 рода. В простом
случае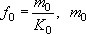 - мощность слоя отложений, создающих
сопротивление между граничным напором
и пластом (это может быть экран под
руслом реки или разделяющий слой в
пластовой водоносной системе),
- мощность слоя отложений, создающих
сопротивление между граничным напором
и пластом (это может быть экран под
руслом реки или разделяющий слой в
пластовой водоносной системе),
 -
коэффициент фильтрации этих отложений.
-
коэффициент фильтрации этих отложений.
Частные случаи ГУ 3 рода:
- - напор на границе неизменен во времени;
- напор на границе неизменен во времени;
-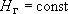 - и к тому же постоянен для всего граничного
элемента;
- и к тому же постоянен для всего граничного
элемента;
-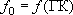 ,
,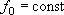 - то же для сопротивления граничного
элемента;
- то же для сопротивления граничного
элемента;
= Особая ситуация при - понятно, что в этом случае должно быть
- понятно, что в этом случае должно быть ,
т.е. на такой границе устанавливается
условие 1 рода (
,
т.е. на такой границе устанавливается
условие 1 рода ( ).
).
|
|
|
Рис.1. Граничное условие 3 рода на контуре водотока (водоема) в ЕСТЕСТВЕННЫХ УСЛОВИЯХ (синий цвет) и при РАБОТЕ ВОДОЗАБОРА (красный цвет) |
• Завершающий пункт схематизации - распределение ИСТОЧНИКОВ-СТОКОВ. Сюда относят:
все виды поступления воды в пласт (источники, балансовый знак +)
все виды расходования воды из пласта (стоки, балансовый знак -),
которые почему-либо не вошли в вышеописанные "стандартные" ГУ.
Например, инфильтрация - это, по сути,
площадное условие 2 рода с заданной
интенсивностью (модулем)
 - расход питания на 1 кв.м площади.
- расход питания на 1 кв.м площади.
Другой распространенный пример: скважины
- нагнетательные, водозаборные, дренажные
и т.п. - это практически точечные (с
радиусом
 )
граничные условия 1 рода, если в скважинах
задан уровень/понижение, а вычисляется
их дебит, или 2 рода (если задан дебит, а
нужно вычислить уровень/понижение в
скважинах).
)
граничные условия 1 рода, если в скважинах
задан уровень/понижение, а вычисляется
их дебит, или 2 рода (если задан дебит, а
нужно вычислить уровень/понижение в
скважинах).
К вопросам расчетной схематизации относится и одна из важнейших и распространенных особенностей решения задач оценки ЭЗ - применение СУПЕРПОЗИЦИИ (СЛОЖЕНИЕ РЕШЕНИЙ). Этот прием, разумеется, является общим для всех задач фильтрации и должен быть уже в принципе рассмотрен в курсе "Гидрогеодинамика".
Его математическое содержание - согласно теореме наложения, линейное дифференциальное уравнение можно разложить на два уравнения, решить каждое отдельно, полученные решения сложить - их сумма будет являться решением общего исходного уравнения. Как это свойство используется при решении задач расчета водозаборных сооружений ?
На примере планового потока (хотя вообще-то мерность неважна):
(0)

- это распределение в плане по
в плане по
 и во времени
и во времени
 в естественных условиях (без водоотбора)
под действием режимообразующих факторов
в естественных условиях (без водоотбора)
под действием режимообразующих факторов
 .
.
При работе водозабора :
(1)
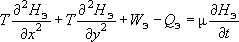
- это распределение в плане по
в плане по
 и во времени
и во времени
 под действием как-то изменившихся (в
результате водоотбора с дебитом
под действием как-то изменившихся (в
результате водоотбора с дебитом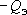 )
режимообразующих факторов
)
режимообразующих факторов
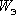 .
.
Согласно принципу суперпозиции, эти уравнения можно алгебраически складывать. Из (0) вычтем (1):
(2)

- это распределение изменений
 в плане по
в плане по
 и во времени
и во времени
 под действием изменений режимообразующих
факторов
под действием изменений режимообразующих
факторов
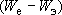 и при дебите водоотбора
и при дебите водоотбора
 .
.
Обозначим
 ,
,
 ;
тогда (2) примет вполне понятный вид:
;
тогда (2) примет вполне понятный вид:
(2а)

Так как нас в конечном счете, в основном,
интересуют только понижения (чтобы
сравнивать их с допустимыми), то можно
ограничиться только решением уравнения
(2а). Если же для каких-то целей необходимо
распределение "полных" напоров
 ,
то можно прямо сложить полученные
понижения (2а) с естественными напорами
(0) и рассматривать их сумму как решение
уравнения (1). В частности, такая
необходимость возникает, если есть
нужда в последующем моделировании
миграции - для этого ведь нужны "полные"
скорости потока.
,
то можно прямо сложить полученные
понижения (2а) с естественными напорами
(0) и рассматривать их сумму как решение
уравнения (1). В частности, такая
необходимость возникает, если есть
нужда в последующем моделировании
миграции - для этого ведь нужны "полные"
скорости потока.
Логичный вопрос: зачем так делать?
Упрощение фильтрационной схемы! Обычно
можно считать (доказательно!), что
развитие депрессии не приведет к
изменению естественных режимообразующих
факторов, важнейшим из которых является
инфильтрация. Следовательно, в уравнениях
(2) или (2а)
 и в них остаются только параметры пласта
и отсутствуют режимообразующие факторы,
оценка которых при разведке - вещь весьма
сложная и не всегда достижимая в нужном
объеме и с нужной степенью достоверности.
и в них остаются только параметры пласта
и отсутствуют режимообразующие факторы,
оценка которых при разведке - вещь весьма
сложная и не всегда достижимая в нужном
объеме и с нужной степенью достоверности.
• Важно: при применении суперпозиции должны быть соответственно трансформированы и граничные условия - если уравнение решается относительно понижений (изменений!), то и ГУ должны быть выражены в изменениях.
- Условия 2 рода приобретают вид:
 При этом: если условия формирования
При этом: если условия формирования
 >
>при эксплуатации не изменяются, то
>
>при эксплуатации не изменяются, то
 ,
т.е. граница 2 рода в этом случае вырождается
в непроницаемую! (и даже не нужно знать
,
т.е. граница 2 рода в этом случае вырождается
в непроницаемую! (и даже не нужно знать
 ).
).
- Условия 3 рода:

Очевидно, что если эксплуатация не
вызывает изменений в поведении и величине
 ,
то
,
то
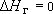 и условие 3 рода упрощается до вида:
и условие 3 рода упрощается до вида:

Два попутных обстоятельства:
а) Изменились балансовые знаки расходов
- дебит водозабора стал положительным
(см. формулу 2а), а приток в пласт через
границу 3 рода стал отрицательным (ведь
 положительное!).
положительное!).
б) Почему может возникнуть изменение
 ?
В наиболее распространенном случае
условия 3 рода (на экранированной реке)
такую возможность следует учитывать,
если за счет инверсии разгрузки и
формирования привлекаемых ресурсов
расход реки существенно уменьшается,
что повлечет за собой и заметное изменение
глубины реки (т.е. уровня реки).
?
В наиболее распространенном случае
условия 3 рода (на экранированной реке)
такую возможность следует учитывать,
если за счет инверсии разгрузки и
формирования привлекаемых ресурсов
расход реки существенно уменьшается,
что повлечет за собой и заметное изменение
глубины реки (т.е. уровня реки).
Итак, общее правило: при решении в понижениях (ур. 2а) на границах учитываются только изменения, возникшие под влиянием эксплуатационных изменений напора в пласте.
То же относится и к источникам-стокам:
- если
 не зависит от
не зависит от
 ,
то
,
то
 ,
т.е. неизменная инфильтрация при решении
в понижениях "исчезает" из решения,
что крайне заманчиво, так как ее (и уж
тем более ее распределение по площади
месторождения) мы обычно знаем очень
неточно;
,
т.е. неизменная инфильтрация при решении
в понижениях "исчезает" из решения,
что крайне заманчиво, так как ее (и уж
тем более ее распределение по площади
месторождения) мы обычно знаем очень
неточно;
- для водозаборной скважины "изменением"
является ее дебит
 ,
так как его не было в естественных
условиях.
,
так как его не было в естественных
условиях.
Список литературы
Для подготовки данной применялись материалы сети Интернет из общего доступа
