Сложные реакции. Типы реакций
Сложные реакции
Под сложными реакциями подразумевают такие реакции, при которых в системе протекает не одна, а несколько (минимум две) реакции с участием тех же реагирующих веществ. В числе сложных реакций следует назвать: обратимые реакции различных порядков, параллельные реакции различных порядков, последовательные реакции (консекутивные), сопряженные. Сюда же можно отнести цепные и фотохимические реакции.
В основе кинетики сложных реакций лежит принцип независимости различных реакций. По этому принципу, если в системе протекает несколько реакций, каждая из них протекает независимо от другой, и каждая подчиняется закону действия масс. Полное изменение системы является суммой изменений, внесенных всеми этими независимыми реакциями. Математически это означает, что кинетическое уравнение сложной реакции является алгебраической суммой кинетических уравнений составляющих её простых решений. Принцип независимости не безусловно общий, т.к. известно взаимовлияние реакций, например, в случае сопряженных реакций. Во многих случаях принцип независимости подтверждается опытом и его применение оказывается полезным и плодотворным.
Обратимые р-ии
Пусть обратимая реакция
 имеет первый порядок в обоих направлениях.
Обозначим через a и b – начальные
концентрации, а через х – уменьшение
концентрации исходного вещества к
моменту времени τ или количество
прореагировавшего вещества.
имеет первый порядок в обоих направлениях.
Обозначим через a и b – начальные
концентрации, а через х – уменьшение
концентрации исходного вещества к
моменту времени τ или количество
прореагировавшего вещества.
В соответствии с принципом независимости суммарная наблюдаемая скорость реакции есть сумма независимых скоростей прямой и обратной реакций, т.е.
 (1)
(1)
Такие реакции, в отличие
от необратимых, доходят в пределе, когда
 ,
не до конца, когда
,
не до конца, когда
 ,
а до состояния равновесия, при котором
общая скорость реакции равна нулю.
,
а до состояния равновесия, при котором
общая скорость реакции равна нулю.
 (2)
(2)
здесь
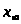 - изменение концентрации исходного
вещества, соответствующее равновесию;
его количество, вступившее в реакцию к
моменту наступления равновесия.
- изменение концентрации исходного
вещества, соответствующее равновесию;
его количество, вступившее в реакцию к
моменту наступления равновесия.
 (3)
(3)
Приравнивая выражение
 к нулю, что соответствует равновесию,
получим:
к нулю, что соответствует равновесию,
получим:
 ,
откуда
,
откуда
 (4)
(4)
Подставляя (4) в (3):
 (5)
(5)

 (6)
(6)
Полученное уравнение
(6) имеет сходство с уравнением для
необратимой реакции 1-го порядка. Разница
в том, что в полученном уравнении вместо
начальной концентрации стоит величина
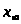 ,
а в правой части уравнения мы имеем
сумму констант прямой и обратной реакции.
,
а в правой части уравнения мы имеем
сумму констант прямой и обратной реакции.
Каждую из констант k1
и k2 можно вычислить, если провести
термодинамический расчет и определить
 .
По величине
.
По величине
 можно вычислить равновесные концентрации
и
можно вычислить равновесные концентрации
и
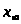 .
Т.о., экспериментально определяя х для
какого-либо τ, можно вычислить каждую
из констант k1 и k2.
.
Т.о., экспериментально определяя х для
какого-либо τ, можно вычислить каждую
из констант k1 и k2.
Параллельные р-ии
Очень часто, особенно в органической химии, исходные вещества реагируют сразу по нескольким направлениям, причем в каждом – со своей скоростью. Например, при нитровании фенола получаются три изомера: орто-, мета-, и пара-. Или при разложении бертолетовой соли:

Рассмотрим простейший случай двух параллельных необратимых реакций первого порядка:
 ,
где:
,
где:
а – начальная концентрация вещества А,
х – количество вещества А, вступившего в реакцию к моменту времени τ,
х1 – количество вещества А, вступившего в реакцию по направлению 1,
х2 – количество вещества А, вступившего в реакцию по направлению 2.
х= х1+ х2 (1)
 ;
;
 (2);
(2);
 (3)
(3)
 (4);
(4);

 (5)
(5)
Уравнение (5) похоже на уравнение, полученное для необратимой реакции 1-го порядка.
Экспериментально
определяя х для какого-то τ по уравнению
(5), вычисляем сумму констант скоростей
 .
Для вычисления каждой константы в
отдельности необходимы дополнительные
условия:
.
Для вычисления каждой константы в
отдельности необходимы дополнительные
условия:

 ;
; ;
; ;
; (6)
(6)
Отношение количеств исходного вещества, вступивших в реакцию в том и другом направлении, в течение всего процесса постоянно.
Используя уравнения (6) и (5), можно вычислить каждую из констант в отдельности. Рассмотрим случай двух параллельных необратимых реакций 2-го порядка.
 ,
где: а и b – концентрации исходных
веществ,
,
где: а и b – концентрации исходных
веществ,
х – убыль концентрации одного из реагирующих веществ.

 ,
,
Аналогично полученному ранее для необратимой реакции 2-го порядка.
Последовательные р-ии
Такие р-ии очень часто встречаются в органической химии. Р-ия протекает через ряд последовательных стадий. Промышленные вещества могут состоять из обычных молекул в дальнейшем вступивших в р-ию либо представляющие свободные атомы или радикалы, обладающие повышенной хим. активностью в подавляющем большинстве случаев. Механизм такой многоступенчатой р-ии неизвестен, поэтому составляют вероятностную схему протекания р-ии по стадиям, опираясь на эту схему, получаю общее кинетическое уравнение суммарной р-ии. Если это уравнение согласуется с опытными данными, то предложенный механизм р-ии является вероятным, но не достоверным. Так как не исключена возможность др. схемы протекания р-ии, которая приведёт к такому же кинетическому уравнению. Точное математическое решение уравнения полученного для последней р-ии с использованием основных законов кинетики целесообразно лишь в простых случаях. В более сложных случаях, если оно вообще возможно приводит к громоздкой формуле, что практически использовать в лучшем случае затруднительно. Рассмотрим решение самого простого случая 2-ух последних односторонних реакций 1-ого порядка, т. е. обозначим а – начальную концентрацию А, х – убыль концентрации исходного вещества А к моменту времени или его количество вступившее в р-ию к моменту времени – количество образовавшегося к моменту времени вещества с (количество вступившего в р-ию вещества В), тогда к моменту концентрации реагирующих веществ будут равны. Концентрации. Скорость первой стадии интеграла. Скорость образования продуктов р-ии. Учитывая ур. 1 можно записать. Полученное Ур. 3 является диф ур. типа ур Лейбница. Решение этого Ур даёт следующие формулы, может быть получено с учётом ур 4, 1. графически интерпретация Ур 4,5,1 приводит к следующему.

Такой вид кривых как показывает анализ, характерен для случаев, когда и различие констант на один порядок. Количество пром. вещества в р-ии систематически изменяется со временем по кривой с максимума. Условия экстремума. Продиф. по ур. 5 приравнивая к 0 полученные уравнения найдём из него выражения для времени, достаточного чтобы промеж. вещество достигло макс. концентрации. Если подставить в полученное выражение для в Ур 5 то после соответствующего преобразования получится следующее из уравнения 7 следует что накопление вещества В не зависит от величины константы, а зависит только от их соотношения, чем меньше, т.е. чем быстрее идёт 1-ая р-ия по сравнению со 2 тем выше лежит максимум кривой и тем ближе он к начальному моменту времени. Скорость накопления продуктов р-ии – вещества С в начале процесса очень мала, этот период называется периодом индукции, по его истечении скорость накопления продуктов резко увеличивается
Сопряжённые р-ии
Р-ии вида А+В→М (1) и A+D→N (2) из которых одна р-ия (2) протекает лишь совместно с др, т.е. индуцируется 1-ой р-ей. При этом вещество В называется индуктором, вещество участвующее в 1-ой и 2-ой р-ии называется актором. Вещество D – акцептор. Связующим звеном в таких р-ях является промежуточный продукт, образованный в результате 1-ой р-ии. Рассмотрим следующий пример: бензол в водном растворе не может непосредственно взаимодействовать с H3O2 ,однако, если в раствор добавить соль 2-х валентного Fe, то в системе на ряду с окислением ионов Fe2+ до Fe3+ начинается окисление бензола до фенола и дифенила, это связано с тем, что при р-ии H3O2+Fe2+ образуется свободный радикал ∙OH Fe2++H3O2→Fe3++OH─+∙OH в присутствии бензола свободный радикал∙OH реагирует со 2 ионом Fe2++∙OH→Fe3++OH─ в присутствии бензола свободный радикал реагирует с молекулой C6H6 отрывая ат H3, C6H6+∙OH→∙C6H5+H3O, ∙C6H5+∙OH→C6H5OH, ∙C6H5 → C6H5-C6H5. В этом примере ионы Fe2+ – индуктор, H3O2 - актор, C6H6 - акцептор. Явление индукции обусловлено, тем, что р-ия окисления C6H6 и Fe2+ идут через общую активную промежуточную частицу ∙OH. При математическом описании сопряжённой р-ии определяется сама модель процесса в этой реакционной системе, скорость этого процесса и будет определять скорость образования продукта р-ии. Шилов классифицировал р-ии на 3 гр. В основе классификации он положил зависимость концентрации индукторов от времени. К 1-ой гр он отнёс р-ии, когда концентрация индукторов во времени убывает, это обычные сопряжённые р-ии. Ко 2-ой группе он отнёс р-ии, когда концентрация индуктора не меняется – это каталитические р-ии. К 3-ей группе он отнёс такие, в которых концентрация индуктора со временем возрастает. Это самоускоряющиеся автокаталитические р-ии.
Цепные р-ии
Многие гомогенные
реакции окисления, расщепления и др.
имеют такие особенности, которые не
могут быть объяснены на основе
рассмотренных нами закономерностях –
это: 1) реакции не подчиняются уравнению
первого, второго и высшего порядков; 2)
скорость реакции очень велика; 3)
необычайная чувствительность к следам
примесей; 4) зависимость скорости реакции
от формы и размеров реакционного сосуда,
а так же материала стенок из которого
изготовлен реакционный сосуд; 5) наличие
индукционного периода, когда реакция
начинается не сразу, а лишь спустя
некоторое время; 6) возможность протекания
реакции в определённом интервале
давления. Все эти положения легко
объясняются цепным механизмом реакции.
Сущность заключается в том, что вначале
в системе образуются активные частицы
чаще всего это свободные остатки и
радикалы. Эти частицы вступают в реакцию,
но при этом вновь возникает валентно
насыщенный остаток и радикал. Процесс
исчезновения и появления каждой активной
частицы и создаёт цепь превращений.
Любая цепная реакция может быть
представлена как реакция, состоящая из
трёх стадий: 1) зарождение активной
частицы (зарождение цепи); 2) рост цепи;
3) обрыв цепи. Рассмотрим это на примере
цепной реакции взаимодействия
 и
и
 :
1) зарождение активной частицы (зарождение
цепи)
:
1) зарождение активной частицы (зарождение
цепи) ;
2) рост цепи
;
2) рост цепи
 ,
,
 ;
3) обрыв цепи
;
3) обрыв цепи
 ,
,
 ,
,
 .
Образовавшиеся молекулы не диссоциируют
на остатки, т к отдали выделенную при
их образовании энергию стенкам сосуда
или молекулам. Число циклов от момента
зарождения цепи до её обрыва называют
длинной цепи. В рассмотренном примере
на один атом
.
Образовавшиеся молекулы не диссоциируют
на остатки, т к отдали выделенную при
их образовании энергию стенкам сосуда
или молекулам. Число циклов от момента
зарождения цепи до её обрыва называют
длинной цепи. В рассмотренном примере
на один атом
 введенного в систему возможно образование
до 1000 и более молекул
введенного в систему возможно образование
до 1000 и более молекул
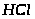 ,
т е длина цепи = 1000. В рассмотренном
примере каждая активная частица вступая
в реакцию порождает лишь одну другую
активную частицу, такие реакции называются
неразветвлёнными цепями. Скорость такой
реакции обычно подчиняется достаточно
простому кинетическому уравнению, но
из-за большого значения длинны цепи
константа скорости имеет аномально
высокое значение.
,
т е длина цепи = 1000. В рассмотренном
примере каждая активная частица вступая
в реакцию порождает лишь одну другую
активную частицу, такие реакции называются
неразветвлёнными цепями. Скорость такой
реакции обычно подчиняется достаточно
простому кинетическому уравнению, но
из-за большого значения длинны цепи
константа скорости имеет аномально
высокое значение.
Цепные реакции с разветвляющимися цепями
Во многих цепных реакциях получается не одна, а две и более активные группы, т е цепь разветвляется. Схематически это можно показать так:
Примером такой цепной
реакции может служить реакция горения
 .
Константа таких процессов была подробно
изучена Семёновым и Гинтельвудом. Они
нашли, что реакции такого типа возможны,
если внешнее давление не превышает
некоторого верхнего предела. Для таких
реакций существует и нижний предел
давления, при переходе через который
реакция прекращается или протекает
медленно и стационарно. Зависимость
скорости этих реакций от давления можно
изобразить следующим графиком:
.
Константа таких процессов была подробно
изучена Семёновым и Гинтельвудом. Они
нашли, что реакции такого типа возможны,
если внешнее давление не превышает
некоторого верхнего предела. Для таких
реакций существует и нижний предел
давления, при переходе через который
реакция прекращается или протекает
медленно и стационарно. Зависимость
скорости этих реакций от давления можно
изобразить следующим графиком:
 -
отвечает нижнему приделу (предел
взрываемости)
-
отвечает нижнему приделу (предел
взрываемости)
 -
отвечает нижнему пределу
-
отвечает нижнему пределу
Область
 отвечает медленной реакции нижнего
предела взрываемости. При достижении
отвечает медленной реакции нижнего
предела взрываемости. При достижении
 ,
скорость быстро растёт и достигает
взрывного течения. После достижения
,
скорость быстро растёт и достигает
взрывного течения. После достижения
 реакция столь же быстро замедляется, а
затем её скорость медленно возрастает
с повышением давления до наступления
теплового взрыва. Зависимость от Т имеет
вид (обоих приделов). Ветвь
реакция столь же быстро замедляется, а
затем её скорость медленно возрастает
с повышением давления до наступления
теплового взрыва. Зависимость от Т имеет
вид (обоих приделов). Ветвь
 отвечает нижнему пределу,
отвечает нижнему пределу,
 -
верхнему. В заштрихованной области
реакция идёт со взрывом, а в не её медленно
и стационарно. Заштрихованная область
называется полуо-вом воспламенения
(взрыва). При Т ниже
-
верхнему. В заштрихованной области
реакция идёт со взрывом, а в не её медленно
и стационарно. Заштрихованная область
называется полуо-вом воспламенения
(взрыва). При Т ниже
 взрывного течения не наблюдается ни
при каких Р. Верхний предел почти не
зависит от формы и размера сосуда, но
сильно зависит от присутствия примесей.
Это объясняется тем, что при больших
давлениях концентрация вещ-в сильно
повышается и обрыв цепи происходит в
объёме при взаимодействии с частицами
примесей. В интервале от
взрывного течения не наблюдается ни
при каких Р. Верхний предел почти не
зависит от формы и размера сосуда, но
сильно зависит от присутствия примесей.
Это объясняется тем, что при больших
давлениях концентрация вещ-в сильно
повышается и обрыв цепи происходит в
объёме при взаимодействии с частицами
примесей. В интервале от
 до
до
 обрыв цепей как на стенках сосуда, так
и в объёме смеси не велики. В реакцию
вовлекается большее количество молекул
реагента и протекает с большой скоростью.
обрыв цепей как на стенках сосуда, так
и в объёме смеси не велики. В реакцию
вовлекается большее количество молекул
реагента и протекает с большой скоростью.

