Расчеты и прогнозирование свойств 2-Метил-3,3-диэтилпентана, Циклобутана, о-Ксилол, 1,2-диметилбензола, 4-Метилпиридина
Федеральное агентство по образованию.
Государственное образовательное учреждение высшего профессионального
образования.
Самарский государственный технический университет.
Кафедра: «Технология органического и нефтехимического синтеза»
Курсовой проект по дисциплине:
«Расчеты и прогнозирование свойств органических соединений»
Выполнил:
Руководитель: доцент, к. х. н.
Самара
2008 г.
Задание 1А
на курсовую работу по дисциплине "Расчеты и прогнозирование свойств органических соединений"
1) Для четырех
соединений, приведенных в таблице,
вычислить
 ,
,
 ,
,
 методом Бенсона по атомам с учетом
первого окружения.
методом Бенсона по атомам с учетом
первого окружения.
2) Для первого
соединения рассчитать
 и
и
 .
.
3) Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить критическую (жидкость-пар) температуру, критическое давление, критический объем, ацентрический фактор.
4) Для первого
соединения рассчитать
 ,
,
 ,
,
 .
Определить фазовое состояние компонента.
.
Определить фазовое состояние компонента.
5) Для первого соединения рассчитать плотность вещества при температуре 730 К и давлении 100 бар. Определить фазовое состояние компонента.
6) Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить плотность насыщенной жидкости. Привести графические зависимости "плотность-температура" для области сосуществования жидкой и паровой фаз. Выполнить их анализ.
7) Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить давление насыщенного пара. Привести графические Р-Т зависимости для области сосуществования жидкой и паровой фаз. Выполнить их проверку и анализ.
8) Для четырех
соединений, приведенных в таблице,
рекомендованными методами вычислить
 и
и
 .
Привести графические зависимости
указанных энтальпий испарения от
температуры для области сосуществования
жидкой и паровой фаз. Выполнить их
анализ.
.
Привести графические зависимости
указанных энтальпий испарения от
температуры для области сосуществования
жидкой и паровой фаз. Выполнить их
анализ.
9) Для первого соединения рассчитать рекомендованными методами вязкость вещества при температуре 730 К и низком давлении.
10) Для первого соединения рассчитать рекомендованными методами вязкость вещества при температуре 730 К и давлении 100 атм.
11) Для первого соединения рассчитать рекомендованными методами теплопроводность вещества при температуре 730 К и низком давлении.
12) Для первого соединения рассчитать рекомендованными методами теплопроводность вещества при температуре 730 К и давлении 100 атм.
Задание №1
Для четырех соединений, приведенных
в таблице, рассчитать

 и
и
 методом Бенсона с учетом первого
окружения.
методом Бенсона с учетом первого
окружения.
2-Метил-3,3-диэтилпентан
Из таблицы Бенсона возьмем
парциальные вклады для

 и
и
 ,
вводим набор поправок:
,
вводим набор поправок:
Поправки на гош взаимодействие
Вводим 8 поправок «алкил-алкил»
Поправка на симметрию:
 ,
,

Таблица 1
|
Кол-во вкладов |
Вклад |
Вклад в энтальпию, кДж/моль |
Вклад |
Вклад в энтропию Дж/К*моль |
Вклад |
Вклад в т/емкость Дж/К*моль |
|
|
СН>3>-(С) |
5 |
-42,19 |
-210,95 |
127,29 |
636,45 |
25,910 |
129,55 |
|
СН-(3С) |
1 |
-7,95 |
-7,95 |
-50,52 |
-50,52 |
19,000 |
19 |
|
С-(4С) |
1 |
2,09 |
2,09 |
-146,92 |
-146,92 |
18,29 |
18,29 |
|
СН>2>-(2С) |
3 |
-20,64 |
-61,92 |
39,43 |
118,29 |
23,02 |
69,06 |
|
∑ |
10 |
-278,73 |
557,3 |
235,9 |
|||
|
гош-поправка |
10 |
3,35 |
33,5 |
вклады в энтропию и теплоемкость для гош-поправок в литературе отсутствуют |
|||
|
поправка на симм. |
σ>нар>=1 |
σ>внутр>=729 |
-54,803 |
||||
|
ΔH>o> |
-245.23 |
ΔS>o> |
502,497 |
ΔС>po> |
235.9 |
Циклобутан
Из таблицы Бенсона возьмем
парциальные вклады для

 и
и
 ,
вводим набор поправок.
,
вводим набор поправок.
Поправки на гош – взаимодействие отсутствуют.
Поправка на внутреннюю симметрию отсутствуют.
Таблица 3
|
Кол-во вкла-дов |
Вклад |
Вклад в энтальпию, кДж/моль |
Вклад |
Вклад в энтропию Дж/К*моль |
Вклад |
Вклад в т/емкость Дж/К*моль |
||
|
СН>2>-(2С) |
4 |
-20,64 |
-82,56 |
39,43 |
157,72 |
23,02 |
92,08 |
|
|
поправка на цикл |
1 |
94,6 |
94,6 |
-116,74 |
-116,74 |
вклад в теплоемкость в литературе отсутствует |
||
|
∑ |
4 |
12,04 |
40,98 |
92,08 |
||||
|
ΔH>o> |
12,04 |
ΔS>o> |
40,98 |
ΔС>po> |
92,08 |
о-Ксилол, 1,2-диметилбензол
Из таблицы Бенсона возьмем
парциальные вклады для

 и
и
 ,
вводим набор поправок.
,
вводим набор поправок.
Поправка на симметрию:

 .
.
Вводим орто-поправку «метил-метил». Из имеющихся в справочной таблице данных оптимально подходит поправка «неполярный/ неполярный».
Таблица 4
|
Кол-во вкла-дов |
Вклад |
Вклад в энтальпию, кДж/моль |
Вклад |
Вклад в энтропию Дж/К*моль |
Вклад |
Вклад в т/емкость Дж/К*моль |
|
|
СН>3>-(С>b>) |
2 |
-42,19 |
-84,38 |
127,29 |
254,58 |
13,56 |
27,12 |
|
C>b>-C |
2 |
23,06 |
46,12 |
-32,19 |
-64,38 |
11,18 |
22,36 |
|
C>b>-H |
4 |
13,81 |
55,24 |
48,26 |
193,04 |
17,16 |
68,64 |
|
∑ |
8 |
16,98 |
383,24 |
118,12 |
|||
|
поправка на симм. – учитывается только для энтропии |
Σ>нар>=1 |
σ>внутр>=9 |
-18,268 |
||||
|
Поправка орто- (неполярный/ неполярный) |
1 |
3,14 |
3,14 |
-6,74 |
-6,740 |
4,69 |
4,69 |
|
ΔH>o> |
20.12 |
S>o> |
358.232 |
С>po> |
122.81 |
4-Метилпиридин
Из таблицы Бенсона возьмем
парциальные вклады для

 и
и
 ,
вводим набор поправок. Поправка на
симметрию:
,
вводим набор поправок. Поправка на
симметрию:


Поскольку в таблице нет специальных вкладов для атомов углерода пиридинового кольца, используем обычные вклады для атомов углерода бензольного кольца (Сb)
Таблица 4
|
Кол-во вкла-дов |
Вклад |
Вклад в энтальпию, кДж/моль |
Вклад |
Вклад в энтропию Дж/К*моль |
Вклад |
Вклад в т/емкость Дж/К*моль |
|
|
СН>3>-(С>b>) |
1 |
-42,19 |
-42,19 |
127,29 |
127,29 |
13,56 |
13,56 |
|
Nb pyrid |
1 |
70,16 |
70,16 |
46,18 |
46,18 |
8,37 |
8,37 |
|
C>b>-(C) |
1 |
23,06 |
23,06 |
-32,19 |
-32,19 |
11,18 |
11,18 |
|
C>b>-H |
4 |
13,81 |
55,24 |
48,26 |
193,04 |
17,16 |
68,64 |
|
∑ |
7 |
106,27 |
334,32 |
101,75 |
|||
|
поправка на симм. |
σ>нар>=1 |
σ>внутр>=3 |
-9.134 |
||||
|
ΔH>o> |
106.27 |
S>o> |
325.186 |
С>po> |
101.75 |
Задание №2
Для первого соединения рассчитать
 и
и

2-Метил-3,3-диэтилпентан
Энтальпия.

где
 -энтальпия
образования вещества при 730К;
-энтальпия
образования вещества при 730К;
 -энтальпия образования вещества при
298К;
-энтальпия образования вещества при
298К;
 -средняя
теплоемкость.
-средняя
теплоемкость.
 ;
;

Для расчета из таблицы Бенсона
выпишем парциальные вклады
 соответственно
для 298К, 400К, 500К, 600К, 800К и путем интерполяции
найдем
соответственно
для 298К, 400К, 500К, 600К, 800К и путем интерполяции
найдем
 для
730К., и
для
730К., и
 для
элементов составляющих соединение.
для
элементов составляющих соединение.
Таблица 5
|
Кол-во вкладов |
С>pi>, 298K, |
С>pi>, 400K, |
С>pi>, 500K, |
С>pi>, 600K, |
С>pi>, 730K, |
С>pi>, 800K, |
||
|
СН>3>-(С) |
5 |
25,910 |
32,820 |
39,950 |
45,170 |
51,235 |
54,5 |
|
|
СН-(3С) |
1 |
19,000 |
25,120 |
30,010 |
33,700 |
37,126 |
38,97 |
|
|
С-(4С) |
1 |
18,29 |
25,66 |
30,81 |
33,99 |
35,758 |
36,71 |
|
|
СН>2>-(2С) |
3 |
23,02 |
29,09 |
34,53 |
39,14 |
43,820 |
46,34 |
|
|
∑ |
10 |
235,900 |
302,150 |
364,160 |
410,960 |
460,516 |
||
|
С |
10 |
8,644 |
11,929 |
14,627 |
16,862 |
18,820 |
19,874 |
|
|
Н>2> |
11 |
28,836 |
29,179 |
29,259 |
29,321 |
29,511 |
29,614 |
|
|
∑ |
403,636 |
440,259 |
468,119 |
491,151 |
512,824 |
 ,
,

 ,
,

 ,
,

 ,
,

 ,
,






Энтропия.


Для расчета из таблицы Бенсона
выпишем парциальные вклады
 соответственно
для 298К, 400К, 500К, 600К, 800К и путем интерполяции
найдем
соответственно
для 298К, 400К, 500К, 600К, 800К и путем интерполяции
найдем
 для
730К.
для
730К.
Таблица 5
|
Кол-во вкладов |
С>pi>, 298K, |
С>pi>, 400K, |
С>pi>, 500K, |
С>pi>, 600K, |
С>pi>, 730K, |
С>pi>, 800K, |
|
|
СН>3>-(С) |
5 |
25,910 |
32,820 |
39,950 |
45,170 |
51,235 |
54,5 |
|
СН-(3С) |
1 |
19,000 |
25,120 |
30,010 |
33,700 |
37,126 |
38,97 |
|
С-(4С) |
1 |
18,29 |
25,66 |
30,81 |
33,99 |
35,758 |
36,71 |
|
СН>2>-(2С) |
3 |
23,02 |
29,09 |
34,53 |
39,14 |
43,820 |
46,34 |
|
∑ |
10 |
235,900 |
302,150 |
364,160 |
410,960 |
460,516 |






Задание №3
Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить (жидкость-пар) температуру, критическое давление, критический объем, ацентрический фактор.
Метод Лидерсена.
Критическую температуру находим по формуле:

где
 -критическая
температура;
-критическая
температура;
 -температура
кипения (берем из таблицы данных);
-температура
кипения (берем из таблицы данных);
 -сумма
парциальных вкладов в критическую
температуру.
-сумма
парциальных вкладов в критическую
температуру.
Критическое давление находится по формуле:

где
 -критическое
давление;
-критическое
давление;
 -молярная
масса вещества;
-молярная
масса вещества;
 -сумма
парциальных вкладов в критическое
давление.
-сумма
парциальных вкладов в критическое
давление.
Критический объем находим по формуле:

где
 -критический
объем;
-критический
объем;
 -сумма
парциальных вкладов в критический
объем.
-сумма
парциальных вкладов в критический
объем.
Ацентрический фактор рассчитывается по формуле:
 ;
;
где
 - ацентрический фактор;
- ацентрический фактор;
 -критическое
давление, выраженное в физических
атмосферах;
-критическое
давление, выраженное в физических
атмосферах;

 -приведенная
нормальная температура кипения вещества;
-приведенная
нормальная температура кипения вещества;
 -нормальная
температура кипения вещества в градусах
Кельвина;
-нормальная
температура кипения вещества в градусах
Кельвина;
 -критическая
температура в градусах Кельвина.
-критическая
температура в градусах Кельвина.
Для расчета, выбираем парциальные вклады для каждого вещества из таблицы составляющих для определения критических свойств по методу Лидерсена.
2-Метил-3,3-диэтилпентан
Выпишем парциальные вклады для температуры, давления и объема:
-
Группа
кол-во
ΔT
ΔP
ΔV
СН>3>-
5
0,1
1,135
275
СН-
1
0,012
0,21
51
С-
1
0
0,21
41
CH>2>
3
0,06
0,681
165
∑
10
0,172
2,236
532
Критическая температура.

Критическое давление.

 .
.

Критический объем.

Ацентрический фактор.
Поскольку для вещества отсутствуют экспериментальные значения критических параметров, используем параметры, полученные методом Лидерсена.
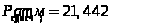 ;
;




4-Метилпиридин
Выпишем парциальные вклады для температуры, давления и объема:
-
Группа
к-во



СН>3>-
1
0,02
0,227
55
-CH= (цикл.)
4
0,044
0,616
148
>C= (цикл.)
1
0,011
0,154
36
=N-(ds)
1
0,007
0,13
13
Сумма
7
0,082
1,127
252
Критическая температура.

Критическое давление.


Критический объем.

Ацентрический фактор.





Циклобутан

Выпишем парциальные вклады для температуры, давления и объема:
-
Группа
кол-во
ΔT
ΔP
ΔV
-CH3-(цикл.)
4
0,052
0,736
178
Сумма
4
0,052
0,736
178
Критическая температура.



Критическое давление.
 ;
;

Критический объем.

Ацентрический фактор.





о-Ксилол, 1,2-диметилбензол
Выпишем парциальные вклады для температуры, давления и объема:
|
Группа |
кол-во |
ΔT |
ΔP |
ΔV |
|
CН>3> |
2 |
0,04 |
0,454 |
110 |
|
-CH= (цикл.) |
4 |
0,044 |
0,616 |
148 |
|
>C= (цикл.) |
2 |
0,022 |
0,308 |
74 |
|
Сумма |
8 |
0,106 |
1,378 |
332 |
Критическая температура.


Критическое давление.


Критический объем.

Ацентрический фактор.




 .
.
Метод Джобака.
Критическую температуру находим по уравнению;

где
 - критическая температура;
- критическая температура;
 - температура кипения (берем из таблицы
данных);
- температура кипения (берем из таблицы
данных);
 -количество
структурных фрагментов в молекуле;
-количество
структурных фрагментов в молекуле;
 -парциальный
вклад в свойство.
-парциальный
вклад в свойство.
Критическое давление находим по формуле:

где
 -критическое
давление в барах;
-критическое
давление в барах;
 -общее
количество атомов в молекуле;
-общее
количество атомов в молекуле;

 -количество
структурных фрагментов;
-количество
структурных фрагментов;
 -парциальный
вклад в свойство.
-парциальный
вклад в свойство.
Критический объем находим по формуле:

где
 -критический
объем в
-критический
объем в
 ;
;

 -количество
структурных фрагментов;
-количество
структурных фрагментов;
 -парциальный
вклад в свойство.
-парциальный
вклад в свойство.
Для расчета, выбираем парциальные вклады в различные свойства для каждого вещества из таблицы составляющих для определения критических свойств по методу Джобака.
2-Метил-3,3-диэтилпентан
Выпишем парциальные вклады для температуры, давления и объема:
|
Группа |
кол-во |
ΔT |
ΔP |
|
СН>3>- |
5 |
0,0705 |
-0,006 |
|
СН- |
1 |
0,0164 |
0,002 |
|
С- |
1 |
0,0067 |
0,0043 |
|
CH>2> |
3 |
0,0567 |
0 |
|
∑ |
10 |
0,1503 |
0,0003 |
Критическая температура.


Критическое давление.
 ;
;

Циклобутан

Выпишем парциальные вклады для температуры, давления и объема:
|
Группа |
к-во |
ΔT |
ΔP |
|
СН>2> (цикл) |
4 |
0,04 |
-0,0112 |
|
Сумма |
4 |
0,04 |
-0,0112 |
Критическая температура.


Критическое давление.
 ;
;
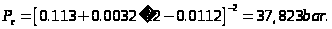
о-Ксилол, 1,2-диметилбензол
Выпишем парциальные вклады для температуры, давления и объема:
|
Группа |
кол-во |
ΔT |
ΔP |
|
CН>3> |
2 |
0,0282 |
-0,0024 |
|
-СН=(цикл) |
4 |
0,0328 |
0,0044 |
|
-С=(цикл) |
2 |
0,0286 |
0,0016 |
|
Сумма |
8 |
0,0896 |
0,0036 |
Критическая температура.



Критическое давление.
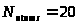 ;
;

4-Метилпиридин
Выпишем парциальные вклады для температуры, давления и объема:
|
Группа |
кол-во |
ΔT |
ΔP |
|
СН>3>- |
1 |
0,0141 |
-0,0012 |
|
-СН=(цикл) |
4 |
0,0328 |
0,0044 |
|
-С=(цикл) |
1 |
0,0143 |
0,0008 |
|
=N-(ds) |
1 |
0,0085 |
0,0076 |
|
Сумма |
7 |
0,0697 |
0,0116 |
Критическая температура.


Критическое давление.
 ;
;

Задание №4
Для первого соединения рассчитать
 ,
,
 и
и
 .
Определить фазовое состояние компонента.
.
Определить фазовое состояние компонента.
Энтальпия
2-Метил-3,3-диэтилпентан
Для расчета
 ,
,
 и
и
 воспользуемся таблицами Ли-Кеслера и
разложением Питцера.
воспользуемся таблицами Ли-Кеслера и
разложением Питцера.

где
 -
энтальпия образования вещества в
стандартном состоянии;
-
энтальпия образования вещества в
стандартном состоянии;
 -энтальпия
образования вещества в заданных условиях;
-энтальпия
образования вещества в заданных условиях;
 и
и
 -изотермические
изменения энтальпии.
-изотермические
изменения энтальпии.
Находим приведенные температуру и давление:


по этим значениям с помощью таблицы Ли-Кесслера и разложения Питцера интерполяцией находим изотермическое изменение энтальпии.


Из правой части выражаем:


Энтропия

где
 -
энтропия вещества в стандартном
состоянии;
-
энтропия вещества в стандартном
состоянии;
 -
энтропия вещества в заданных условиях;
-
энтропия вещества в заданных условиях; -
ацентрический фактор.
-
ацентрический фактор.
Критические параметры вещества определяем методом Лидерсена.

 ;
R=8,314Дж/моль*К
;
R=8,314Дж/моль*К


Находим приведенные температуру и давление:


по этим значениям с помощью таблицы Ли-Кесслера и разложения Питцера интерполяцией находим изотермическое изменение энтропии.


Из правой части выражаем:

Теплоемкость.

где
 - теплоемкость соединения при стандартных
условиях;
- теплоемкость соединения при стандартных
условиях;
 -
теплоемкость соединения при заданных
условиях;
-
теплоемкость соединения при заданных
условиях;
 -ацентрический
фактор.
-ацентрический
фактор.
Критические параметры вещества определяем методом Лидерсена.

 ;
R=8,314Дж/моль*К
;
R=8,314Дж/моль*К


Находим приведенные температуру и давление:


по этим значениям с помощью таблицы Ли-Кесслера и разложения Питцера интерполяцией находим изотермическое изменение теплоемкости.

 Дж/моль*К
Дж/моль*К
Из правой части выражаем:

Задание №5
Для первого соединения рассчитать плотность вещества при температуре 730 К и давлении 100 бар. Определить фазовое состояние компонента.
Для определения плотности вещества воспользуемся методом прогнозирования плотности индивидуальных веществ с использованием коэффициента сжимаемости.

где
 -плотность
вещества; М- молярная масса; V-объем.
-плотность
вещества; М- молярная масса; V-объем.
Для данного вещества найдем коэффициент сжимаемости с использованием таблицы Ли-Кесслера по приведенным температуре и давлении.
Коэффициент сжимаемости находится по разложению Питцера:

где Z-коэффициент
сжимаемости;
 -ацентрический
фактор.
-ацентрический
фактор.
Приведенную температуру найдем
по формуле

где
 -приведенная
температура в К ; Т-температура вещества
в К;
-приведенная
температура в К ; Т-температура вещества
в К;
 -критическая
температура в К.
-критическая
температура в К.
Приведенное давление найдем по
формуле
 ;
где
;
где
 -
приведенное; Р и
-
приведенное; Р и давление и критическое давление в атм.
соответственно.
давление и критическое давление в атм.
соответственно.
Критические параметры вещества определяем методом Лидерсена.

 ;
R=8,314Дж/моль*К
;
R=8,314Дж/моль*К


Находим приведенные температуру и давление:


Коэффициент сжимаемости найдем из разложения Питцера:
путем интерполяции находим
 и
и .
.
 =0,6773;
=0,6773;
 =-0,0280;
=-0,0280;

Из уравнения Менделеева-Клайперона
 ,
,
где P-давление; V-объем; Z- коэффициент сжимаемости; R-универсальная газовая постоянная (R=82.04); T-температура;
выразим объем:

М=142,29 г/моль.

Фазовое состояние вещества определяем по таблицам Ли-Кесслера, по приведенным параметрам температуры и давления. Ячейка, соответствующая данным приведенным параметрам находится под линией бинодаля, следовательно данное вещество при 730К и 100 бар – газ.
Задание №6
Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить плотность насыщенной жидкости. Привести графические зависимости «плотность-температура» для области существования жидкой и паровой фаз. Выполнить анализ.
Для вычисления плотности насыщенной жидкости воспользуемся методом Ганна-Ямады.

где
 -плотность
насыщенной жидкости; М -молярная масса
вещества;
-плотность
насыщенной жидкости; М -молярная масса
вещества;
 -молярный
объем насыщенной жидкости.
-молярный
объем насыщенной жидкости.

где
 -масштабирующий
параметр;
-масштабирующий
параметр;
 -ацентрический
фактор;
-ацентрический
фактор;
 и Г-функции приведенной температуры.
и Г-функции приведенной температуры.


2-Метил-3,3-диэтилпентан
 в промежутке температур от 298 до
475 К вычислим по формуле:
в промежутке температур от 298 до
475 К вычислим по формуле:

В промежутке температур от 475 до 600 К вычислим по формуле:

В промежутке температур от 298 до 600 К вычислим Г по формуле:

Находим масштабирующий параметр:
Полученные результаты сведем в таблицу:
-
T, К
T>r>
V>r(0)>
V>sc>
Г
V>s>
ρ>s> ,г/см3
187,2738
0,3
0,3252
328,7164
0,2646
95,8685
1.3312
218,4861
0,35
0,3331
328,7164
0,2585
109,5005
1,2994
249,6983
0,4
0,3421
328,7164
0,2521
112,4670
1,2651
280,9106
0,45
0,3520
328,7164
0,2456
115,6993
1,2298
312,1229
0,5
0,3625
328,7164
0,2387
119,1650
1,1940
343,3352
0,55
0,3738
328,7164
0,2317
122,8869
1,1579
374,5475
0,6
0,3862
328,7164
0,2244
126,9426
1,1209
405,7598
0,65
0,3999
328,7164
0,2168
131,4645
1,0823
436,9721
0,7
0,4157
328,7164
0,2090
136,6402
1,0413
468,1844
0,75
0,4341
328,7164
0,2010
142,7120
0,9970
499,3967
0,8
0,4563
328,7164
0,1927
149,9773
0,9487
530,609
0,85
0,4883
328,7164
0,1842
160,4985
0,8865
561,8213
0,9
0,5289
328,7164
0,1754
173,8487
0,8185
580,5486
0,93
0,5627
328,7164
0,1701
184,9601
0,7693
593,0336
0,95
0,5941
328,7164
0,1664
195,2829
0,7286
605,5185
0,97
0,6410
328,7164
0,1628
210,7108
0,6753
611,7609
0,98
0,6771
328,7164
0,1609
222,5759
0,6393
618,0034
0,99
0,7348
328,7164
0,1591
241,5476
0,5891
Циклобутан
-
T, К
T>r>
V>r(0)>
V>sc>
Г
V>s>
ρ>s> ,г/см3
139,0728
0,3
0,3252
752,1954
0,2646
233,3600
0,2404
162,2516
0,35
0,3331
752,1954
0,2585
239,3309
0,2344
185,4304
0,4
0,3421
752,1954
0,2521
246,0977
0,2280
208,6092
0,45
0,3520
752,1954
0,2456
253,4727
0,2214
231,788
0,5
0,3625
752,1954
0,2387
261,3882
0,2147
254,9668
0,55
0,3738
752,1954
0,2317
269,8969
0,2079
278,1456
0,6
0,3862
752,1954
0,2244
279,1725
0,2010
301,3244
0,65
0,3999
752,1954
0,2168
289,5111
0,1938
324,5032
0,7
0,4157
752,1954
0,2090
301,3316
0,1862
347,682
0,75
0,4341
752,1954
0,2010
315,1769
0,1780
370,8608
0,8
0,4563
752,1954
0,1927
331,7151
0,1691
394,0396
0,85
0,4883
752,1954
0,1842
355,5282
0,1578
417,2183
0,9
0,5289
752,1954
0,1754
385,7055
0,1455
431,1256
0,93
0,5627
752,1954
0,1701
410,7518
0,1366
440,3971
0,95
0,5941
752,1954
0,1664
433,9578
0,1293
449,6687
0,97
0,6410
752,1954
0,1628
468,5486
0,1197
454,3044
0,98
0,6771
752,1954
0,1609
495,0958
0,1133
458,9402
0,99
0,7348
752,1954
0,1591
537,4744
0,1044
о-Ксилол, 1,2-диметилбензол
|
T, К |
Tr |
Vr(0) |
Vsc |
Г |
Vs |
ρs ,г/см3 |
|
189,3122 |
0,3 |
0,3252 |
374,9598 |
0,2646 |
112,2652 |
0,9637 |
|
220,8642 |
0,35 |
0,3331 |
374,9598 |
0,2585 |
115,2382 |
0,9388 |
|
252,4163 |
0,4 |
0,3421 |
374,9598 |
0,2521 |
118,6036 |
0,9122 |
|
283,9683 |
0,45 |
0,3520 |
374,9598 |
0,2456 |
122,2723 |
0,8848 |
|
315,5203 |
0,5 |
0,3625 |
374,9598 |
0,2387 |
126,2126 |
0,8572 |
|
347,0724 |
0,55 |
0,3738 |
374,9598 |
0,2317 |
130,4511 |
0,8293 |
|
378,6244 |
0,6 |
0,3862 |
374,9598 |
0,2244 |
135,0732 |
0,8009 |
|
410,1764 |
0,65 |
0,3999 |
374,9598 |
0,2168 |
140,2236 |
0,7715 |
|
441,7285 |
0,7 |
0,4157 |
374,9598 |
0,2090 |
146,1077 |
0,7404 |
|
473,2805 |
0,75 |
0,4341 |
374,9598 |
0,2010 |
152,9918 |
0,7071 |
|
504,8325 |
0,8 |
0,4563 |
374,9598 |
0,1927 |
161,2043 |
0,6711 |
|
536,3846 |
0,85 |
0,4883 |
374,9598 |
0,1842 |
172,9800 |
0,6254 |
|
567,9366 |
0,9 |
0,5289 |
374,9598 |
0,1754 |
187,8885 |
0,5758 |
|
586,8678 |
0,93 |
0,5627 |
374,9598 |
0,1701 |
200,2365 |
0,5403 |
|
599,4886 |
0,95 |
0,5941 |
374,9598 |
0,1664 |
211,6540 |
0,5111 |
|
612,1095 |
0,97 |
0,6410 |
374,9598 |
0,1628 |
228,6393 |
0,4732 |
|
618,4199 |
0,98 |
0,6771 |
374,9598 |
0,1609 |
241,6545 |
0,4477 |
|
624,7303 |
0,99 |
0,7348 |
374,9598 |
0,1591 |
262,4056 |
0,4123 |
4-Метилпиридин
|
T, К |
Tr |
Vr(0) |
Vsc |
Г |
Vs |
ρs ,г/см3 |
|
195,4767 |
0,3 |
0,3252 |
326,7747 |
0,2646 |
98,5374 |
0,9451 |
|
228,0562 |
0,35 |
0,3331 |
326,7747 |
0,2585 |
101,1289 |
0,9209 |
|
260,6356 |
0,4 |
0,3421 |
326,7747 |
0,2521 |
104,0632 |
0,8949 |
|
293,2151 |
0,45 |
0,3520 |
326,7747 |
0,2456 |
107,2617 |
0,8682 |
|
325,7945 |
0,5 |
0,3625 |
326,7747 |
0,2387 |
110,6966 |
0,8413 |
|
358,374 |
0,55 |
0,3738 |
326,7747 |
0,2317 |
114,3910 |
0,8141 |
|
390,9534 |
0,6 |
0,3862 |
326,7747 |
0,2244 |
118,4194 |
0,7864 |
|
423,5329 |
0,65 |
0,3999 |
326,7747 |
0,2168 |
122,9085 |
0,7577 |
|
456,1123 |
0,7 |
0,4157 |
326,7747 |
0,2090 |
128,0379 |
0,7274 |
|
488,6918 |
0,75 |
0,4341 |
326,7747 |
0,2010 |
134,0403 |
0,6948 |
|
521,2712 |
0,8 |
0,4563 |
326,7747 |
0,1927 |
141,2029 |
0,6595 |
|
553,8507 |
0,85 |
0,4883 |
326,7747 |
0,1842 |
151,4816 |
0,6148 |
|
586,4301 |
0,9 |
0,5289 |
326,7747 |
0,1754 |
164,4974 |
0,5661 |
|
605,9778 |
0,93 |
0,5627 |
326,7747 |
0,1701 |
175,2823 |
0,5313 |
|
619,0096 |
0,95 |
0,5941 |
326,7747 |
0,1664 |
185,2584 |
0,5027 |
|
632,0414 |
0,97 |
0,6410 |
326,7747 |
0,1628 |
200,1054 |
0,4654 |
|
638,5573 |
0,98 |
0,6771 |
326,7747 |
0,1609 |
211,4855 |
0,4404 |
|
645,0731 |
0,99 |
0,7348 |
326,7747 |
0,1591 |
229,6344 |
0,4056 |
Задание №7
Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить давление насыщенного пара. Привести графические P-T зависимости для области существования жидкой и паровой фаз. Выполнить анализ.
Для вычисления давления насыщенного пара воспользуемся корреляциями
Ли-Кесслера, Риделя и Амброуза-Уолтона.
2-Метил-3,3-диэтилпентан
Корреляция Ли-Кеслера.
Она основана на использовании принципа соответственных состояний.



Давление P>vp
>определяем из приведенного
давления насыщенных паров P>vp,r>
и критического давления данного вещества:
 .
Критическое давление определяем методом
Лидерсена, поскольку для данного вещества
экспериментальные данные отсутствуют.
.
Критическое давление определяем методом
Лидерсена, поскольку для данного вещества
экспериментальные данные отсутствуют.
-
Т
Т>r>
f>(0)>
f>(1)>
P>vp,r>
P>vp, >bar
298
0,48
-5,8100
-7,4402
0,0002
0.0031
323
0,52
-4,9185
-5,9645
0,0007
0.0131
348
0,56
-4,1614
-4,7734
0,0024
0.0441
373
0,60
-3,5110
-3,8045
0,0068
0.1222
398
0,64
-2,9470
-3,0118
0,0162
0.2907
423
0,68
-2,4535
-2,3609
0,0343
0.6115
448
0,72
-2,0187
-1,8251
0,0652
1.1638
473
0,76
-1,6329
-1,3839
0,1139
2.0414
498
0,80
-1,2886
-1,0210
0,1852
3.3502
523
0,84
-0,9796
-0,7234
0,2832
5.2080
548
0,88
-0,7010
-0,4808
0,4113
7.7496
573
0,92
-0,4487
-0,2847
0,5714
11.1385
Корреляция Риделя








где
 - приведенная температура кипения.
- приведенная температура кипения.







-
Т
Т>r>
P>vp,r>
P>vp, >bar
298
0,48
0,0001
0.0031
323
0,52
0,0006
0.0130
348
0,56
0,0020
0.0436
373
0,60
0,0056
0.1206
398
0,64
0,0132
0.2868
423
0,68
0,0278
0.6031
448
0,72
0,0529
1.1487
473
0,76
0,0928
2.0173
498
0,80
0,1526
3.3157
523
0,84
0,2377
5.1638
548
0,88
0,3544
7.6992
573
0,92
0,5104
11.0895
Метод Амброуза-Уолтона.




где

-
Т
Т>r>
τ
f>(0)>
f>(1)>
f>(2)>
P>vp,r>
P>vp, >bar
298
0,48
0,52
-5,8518
-7,4767
-0,2979
0,0001
0.0032
323
0,52
0,48
-4,9751
-6,0420
-0,2096
0,0006
0.0138
348
0,56
0,44
-4,2318
-4,8990
-0,1374
0,0021
0.0458
373
0,60
0,40
-3,5932
-3,9769
-0,0810
0,0058
0.1254
398
0,64
0,36
-3,0381
-3,2243
-0,0393
0,0136
0.2947
423
0,68
0,32
-2,5505
-2,6033
-0,0108
0,0283
0.6139
448
0,72
0,28
-2,1179
-2,0853
0,0062
0,0534
1.1608
473
0,76
0,24
-1,7307
-1,6487
0,0138
0,0934
2.0290
498
0,80
0,20
-1,3813
-1,2769
0,0141
0,1531
3.3263
523
0,84
0,16
-1,0634
-0,9570
0,0094
0,2381
5.1741
548
0,88
0,12
-0,7720
-0,6785
0,0021
0,3549
7.7100
573
0,92
0,08
-0,5025
-0,4330
-0,0050
0,5107
11.0960
Циклобутан

Корреляция Ли-Кеслера
Корреляция Ли-Кеслера.
Она основана на использовании принципа соответственных состояний.



Давление P>vp
>определяем из приведенного
давления насыщенных паров P>vp,r>
и экспериментального критического
давления данного вещества, bar:
 .
.
-
Т
Т>r>
f>(0)>
f>(1)>
P>vp,r>
P>vp, >bar
298
0.65
-2.9116
-3.0829
0.0286
1.4249
323
0.70
-2.2792
-2.2739
0.0636
3.1757
348
0.76
-1.7401
-1.6438
0.1245
6.2111
373
0.81
-1.2730
-1.1464
0.2203
10.9946
398
0.87
-0.8614
-0.7463
0.3615
18.0404
423
0.92
-0.4922
-0.4147
0.5606
27.9717
448
0.97
-0.1541
-0.1279
0.8346
41.6465
Корреляция Риделя.








где
 - приведенная температура кипения.
- приведенная температура кипения.
|
А |
В |
С |
D |
θ |
α>c> |
ψ |
|
8,1962 |
8,4304 |
-3,2830 |
0,2342 |
-0,2342 |
6,5525 |
3,0295 |
|
Т |
Т>r> |
P>vp,r> |
P>vp, >bar |
|
298 |
0,64 |
0.0342 |
1.7082 |
|
323 |
0,70 |
0.0727 |
3.6290 |
|
348 |
0,75 |
0.1370 |
6.8383 |
|
373 |
0,80 |
0.2356 |
11.7557 |
|
398 |
0,86 |
0.3776 |
18.8422 |
|
423 |
0,91 |
0.5742 |
28.6547 |
|
448 |
0,97 |
0.8408 |
41.9569 |
Корреляция Амброуза-Уолтона.




где

|
Т |
Т>r> |
τ |
f>(0)> |
f>(1)> |
f>(2)> |
P>vp,r> |
P>vp, >bar |
|
298 |
0.65 |
0.35 |
-2.9073 |
-3.0540 |
-0.0308 |
0.0288 |
1.4377 |
|
323 |
0.70 |
0.30 |
-2.2794 |
-2.2749 |
0.0009 |
0.0636 |
3.1748 |
|
348 |
0.76 |
0.24 |
-1.7417 |
-1.6607 |
0.0137 |
0.1239 |
6.1834 |
|
373 |
0.81 |
0.19 |
-1.2741 |
-1.1670 |
0.0130 |
0.2193 |
10.9420 |
|
398 |
0.87 |
0.13 |
-0.8614 |
-0.7625 |
0.0045 |
0.3604 |
17.9837 |
|
423 |
0.92 |
0.08 |
-0.4917 |
-0.4235 |
-0.0052 |
0.5596 |
27.9261 |
|
448 |
0.97 |
0.03 |
-0.1545 |
-0.1306 |
-0.0074 |
0.8335 |
41.5906 |
о-Ксилол, 1,2-диметилбензол
Корреляция Ли-Кесслера.
Корреляция Ли-Кесслера.
Она основана на использовании принципа соответственных состояний.



Давление P>vp
>определяем из приведенного
давления насыщенных паров P>vp,r>
и экспериментального критического
давления данного вещества, bar:
 .
.
|
Т |
Т>r> |
f>(0)> |
f>(1)> |
P>vp,r> |
P>vp, >bar |
|
298 |
0.47 |
-5.9985 |
-7.8289 |
0.0002 |
0.0078 |
|
323 |
0.51 |
-5.1032 |
-6.3434 |
0.0008 |
0.0305 |
|
348 |
0.55 |
-4.3431 |
-5.1444 |
0.0026 |
0.0951 |
|
373 |
0.59 |
-3.6900 |
-4.1686 |
0.0067 |
0.2482 |
|
398 |
0.63 |
-3.1232 |
-3.3688 |
0.0153 |
0.5624 |
|
423 |
0.67 |
-2.6264 |
-2.7093 |
0.0309 |
1.1370 |
|
448 |
0.71 |
-2.1872 |
-2.1622 |
0.0569 |
2.0947 |
|
473 |
0.75 |
-1.7955 |
-1.7058 |
0.0972 |
3.5767 |
|
498 |
0.79 |
-1.4431 |
-1.3222 |
0.1559 |
5.7387 |
|
523 |
0.83 |
-1.1233 |
-0.9969 |
0.2378 |
8.7507 |
|
548 |
0.87 |
-0.8305 |
-0.7175 |
0.3479 |
12.8031 |
Корреляция Риделя








где
 приведенная
температура кипения.
приведенная
температура кипения.
|
А |
В |
С |
D |
θ |
αc |
ψ |
|
10,3483 |
10,6440 |
-5,1318 |
0,2957 |
-0,2957 |
7,2862 |
1,9765 |
|
Т |
Т>r> |
P>vp,r> |
P>vp, >bar |
|
298 |
0,47 |
0.0002 |
0.0090 |
|
323 |
0,51 |
0.0009 |
0.0341 |
|
348 |
0,55 |
0.0028 |
0.1037 |
|
373 |
0,59 |
0.0072 |
0.2657 |
|
398 |
0,63 |
0.0161 |
0.5928 |
|
423 |
0,67 |
0.0322 |
1.1840 |
|
448 |
0,71 |
0.0587 |
2.1604 |
|
473 |
0,75 |
0.0995 |
3.6609 |
|
498 |
0,79 |
0.1587 |
5.8384 |
|
523 |
0,83 |
0.2408 |
8.8601 |
|
548 |
0,87 |
0.3509 |
12.9136 |
Корреляция Амброуза-Уолтона.




где

|
Т |
Т>r> |
τ |
f>(0)> |
f>(1)> |
f>(2)> |
P>vp,r> |
P>vp, >bar |
|
298 |
0.47 |
0.53 |
-5.9605 |
-7.6606 |
-0.3088 |
0.0002 |
0.0083 |
|
323 |
0.51 |
0.49 |
-5.0743 |
-6.1998 |
-0.2196 |
0.0009 |
0.0322 |
|
348 |
0.55 |
0.45 |
-4.3230 |
-5.0354 |
-0.1460 |
0.0027 |
0.0990 |
|
373 |
0.59 |
0.41 |
-3.6777 |
-4.0956 |
-0.0880 |
0.0069 |
0.2549 |
|
398 |
0.63 |
0.37 |
-3.1170 |
-3.3283 |
-0.0447 |
0.0155 |
0.5707 |
|
423 |
0.67 |
0.33 |
-2.6244 |
-2.6950 |
-0.0145 |
0.0311 |
1.1427 |
|
448 |
0.71 |
0.29 |
-2.1877 |
-2.1667 |
0.0041 |
0.0568 |
2.0914 |
|
473 |
0.75 |
0.25 |
-1.7970 |
-1.7215 |
0.0131 |
0.0967 |
3.5582 |
|
498 |
0.79 |
0.21 |
-1.4445 |
-1.3425 |
0.0145 |
0.1550 |
5.7024 |
|
523 |
0.83 |
0.17 |
-1.1240 |
-1.0166 |
0.0106 |
0.2364 |
8.6999 |
|
548 |
0.87 |
0.13 |
-0.8304 |
-0.7332 |
0.0037 |
0.3464 |
12.7464 |

4-Метилпиридин

Корреляция Ли-Кеслера.
Корреляция Ли-Кеслера.
Она основана на использовании принципа соответственных состояний.



Давление P>vp
>определяем из приведенного
давления насыщенных паров P>vp,r>
и экспериментального критического
давления данного вещества, bar:
 .
.
-
Т
Т>r>
f>(0)>
f>(1)>
P>vp,r>
P>vp, >bar
298
0.46
-6.2901
-8.3277
0.0002
0.0086
323
0.50
-5.3700
-6.7782
0.0007
0.0328
348
0.54
-4.5886
-5.5248
0.0023
0.1006
373
0.58
-3.9174
-4.5021
0.0059
0.2596
398
0.62
-3.3348
-3.6618
0.0133
0.5832
423
0.65
-2.8243
-2.9671
0.0266
1.1720
448
0.69
-2.3733
-2.3897
0.0489
2.1505
473
0.73
-1.9714
-1.9070
0.0832
3.6618
498
0.77
-1.6103
-1.5010
0.1332
5.8628
523
0.81
-1.2833
-1.1569
0.2028
8.9226
548
0.85
-0.9845
-0.8623
0.2960
13.0255
573
0.89
-0.7090
-0.6066
0.4178
18.3822
598
0.93
-0.4526
-0.3805
0.5739
25.2495
623
0.96
-0.2115
-0.1759
0.7719
33.9624
Корреляция Риделя








где
 приведенная
температура кипения.
приведенная
температура кипения.
|
А |
В |
С |
D |
θ |
αc |
ψ |
|
10,0617 |
10,3492 |
-4,8855 |
0,2875 |
-0,2875 |
7,1885 |
2,2628 |
|
Т |
Т>r> |
P>vp,r> |
P>vp, >bar |
|
298 |
0.46 |
0.0002 |
0.0079 |
|
323 |
0.50 |
0.0007 |
0.0305 |
|
348 |
0.54 |
0.0021 |
0.0945 |
|
373 |
0.58 |
0.0056 |
0.2458 |
|
398 |
0.62 |
0.0127 |
0.5568 |
|
423 |
0.65 |
0.0256 |
1.1268 |
|
448 |
0.69 |
0.0473 |
2.0805 |
|
473 |
0.73 |
0.0810 |
3.5624 |
|
498 |
0.77 |
0.1303 |
5.7323 |
|
523 |
0.81 |
0.1992 |
8.7638 |
|
548 |
0.85 |
0.2920 |
12.8470 |
|
573 |
0.89 |
0.4136 |
18.2002 |
|
598 |
0.93 |
0.5702 |
25.0894 |
|
623 |
0.96 |
0.7696 |
33.8611 |
Корреляция Амброуза-Уолтона.




где

|
Т |
Т>r> |
τ |
f>(0)> |
f>(1)> |
f>(2)> |
P>vp,r> |
P>vp, >bar |
|
298 |
0.46 |
0.54 |
-6.2496 |
-8.1557 |
-0.3377 |
0.0002 |
0.0092 |
|
323 |
0.50 |
0.50 |
-5.3381 |
-6.6253 |
-0.2461 |
0.0008 |
0.0347 |
|
348 |
0.54 |
0.46 |
-4.5656 |
-5.4035 |
-0.1693 |
0.0024 |
0.1051 |
|
373 |
0.58 |
0.42 |
-3.9024 |
-4.4161 |
-0.1074 |
0.0061 |
0.2676 |
|
398 |
0.62 |
0.38 |
-3.3264 |
-3.6093 |
-0.0599 |
0.0135 |
0.5939 |
|
423 |
0.65 |
0.35 |
-2.8209 |
-2.9429 |
-0.0255 |
0.0269 |
1.1816 |
|
448 |
0.69 |
0.31 |
-2.3729 |
-2.3869 |
-0.0028 |
0.0489 |
2.1524 |
|
473 |
0.73 |
0.27 |
-1.9726 |
-1.9184 |
0.0100 |
0.0829 |
3.6487 |
|
498 |
0.77 |
0.23 |
-1.6119 |
-1.5198 |
0.0146 |
0.1325 |
5.8301 |
|
523 |
0.81 |
0.19 |
-1.2843 |
-1.1775 |
0.0131 |
0.2016 |
8.8720 |
|
548 |
0.85 |
0.15 |
-0.9848 |
-0.8804 |
0.0076 |
0.2947 |
12.9654 |
|
573 |
0.89 |
0.11 |
-0.7087 |
-0.6199 |
0.0003 |
0.4164 |
18.3231 |
|
598 |
0.93 |
0.07 |
-0.4523 |
-0.3885 |
-0.0061 |
0.5726 |
25.1939 |
|
623 |
0.96 |
0.04 |
-0.2117 |
-0.1794 |
-0.0081 |
0.7705 |
33.9003 |

Задание №8
Для четырех соединений, приведенных
в таблице, рекомендованными методами
вычислить
 и
и

2-Метил-3,3-диэтилпентан

Уравнение Ли-Кесслера.
 ;
;
 для
стандартных условий
для
стандартных условий


приведенную температуру найдем
как
 ,
в интервале от 298К до
,
в интервале от 298К до
 .приведенное
давление возьмем из задания №7
.приведенное
давление возьмем из задания №7
 ацентрический фактор
ацентрический фактор
 возьмем из задания №3.
возьмем из задания №3.
|
Т |
Т>r> |
Δ>v>Z |
Ψ |
Δ>v>H0>T> |
Δ>v>H>T> |
|
298 |
0,48 |
0.9994 |
9.0993 |
47225.03 |
47194.42 |
|
323 |
0,52 |
0.9978 |
8.8462 |
45911.38 |
45811.13 |
|
348 |
0,56 |
0.9941 |
8.5982 |
44624.37 |
44362.26 |
|
373 |
0,60 |
0.9867 |
8.3576 |
43376.00 |
42800.33 |
|
398 |
0,64 |
0.9738 |
8.1276 |
42182.22 |
41078.80 |
|
423 |
0,68 |
0.9537 |
7.9121 |
41063.87 |
39162.58 |
|
448 |
0,72 |
0.9247 |
7.7164 |
40047.76 |
37032.49 |
|
473 |
0,76 |
0.8854 |
7.5468 |
39167.78 |
34680.94 |
|
498 |
0,80 |
0.8344 |
7.4117 |
38466.32 |
32097.77 |
|
523 |
0,84 |
0.7697 |
7.3210 |
37995.69 |
29244.08 |
|
548 |
0,88 |
0.6876 |
7.2871 |
37819.85 |
26003.74 |
|
573 |
0,92 |
0.5806 |
7.3249 |
38016.18 |
22072.67 |
Корреляция Риделя.
 ;
;

 для стандартных условий
для стандартных условий
 ,
,
R=8.314,
 - возьмем из задания №3,
- возьмем из задания №3,
 -
возьмем из задания №7,
-
возьмем из задания №7,
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
|
Т |
Т>r> |
Δ>v>Z |
Ψ |
Δ>v>H0>T> |
Δ>v>H>T> |
|
298 |
0,48 |
0.9994 |
9.0614 |
47028.71 |
46998.28 |
|
323 |
0,52 |
0.9978 |
8.8169 |
45759.66 |
45660.48 |
|
348 |
0,56 |
0.9942 |
8.5775 |
44516.96 |
44258.32 |
|
373 |
0,60 |
0.9869 |
8.3454 |
43312.43 |
42745.02 |
|
398 |
0,64 |
0.9742 |
8.1237 |
42161.87 |
41074.25 |
|
423 |
0,68 |
0.9543 |
7.9164 |
41085.87 |
39210.13 |
|
448 |
0,72 |
0.9257 |
7.7285 |
40110.90 |
37131.67 |
|
473 |
0,76 |
0.8869 |
7.5666 |
39270.50 |
34828.48 |
|
498 |
0,80 |
0.8363 |
7.4387 |
38606.53 |
32287.01 |
|
523 |
0,84 |
0.7719 |
7.3547 |
38170.72 |
29464.48 |
|
548 |
0,88 |
0.6901 |
7.3269 |
38026.26 |
26240.29 |
|
573 |
0,92 |
0.5831 |
7.3699 |
38249.66 |
22304.19 |
Корреляция Амброуза-Уолтона.
 ;
;

 для
стандартных условий
для
стандартных условий
 ;
;
приведенную температуру найдем
как
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
приведенное давление возьмем из задания №7
возьмем из задания №7
 ; ацентрический фактор
; ацентрический фактор
 возьмем из задания №3.
возьмем из задания №3.
|
Т |
Т>r> |
τ |
Δ>v>Z |
Ψ |
Δ>v>H0>T> |
Δ>v>H>T> |
|
298 |
0,48 |
0,52 |
0.9993 |
9.0905 |
47179.65 |
47147.28 |
|
323 |
0,52 |
0,48 |
0.9977 |
8.7807 |
45571.50 |
45466.84 |
|
348 |
0,56 |
0,44 |
0.9939 |
8.4977 |
44102.66 |
43833.36 |
|
373 |
0,60 |
0,40 |
0.9864 |
8.2427 |
42779.57 |
42197.02 |
|
398 |
0,64 |
0,36 |
0.9735 |
8.0166 |
41605.80 |
40502.44 |
|
423 |
0,68 |
0,32 |
0.9535 |
7.8196 |
40583.46 |
38696.73 |
|
448 |
0,72 |
0,28 |
0.9249 |
7.6522 |
39714.77 |
36732.49 |
|
473 |
0,76 |
0,24 |
0.8862 |
7.5153 |
39004.10 |
34564.92 |
|
498 |
0,80 |
0,20 |
0.8357 |
7.4106 |
38460.70 |
32143.02 |
|
523 |
0,84 |
0,16 |
0.7714 |
7.3417 |
38103.16 |
29392.38 |
|
548 |
0,88 |
0,12 |
0.6895 |
7.3156 |
37967.78 |
26179.69 |
|
573 |
0,92 |
0,08 |
0.5828 |
7.3466 |
38128.55 |
22220.77 |

Циклобутан

Уравнение Ли-Кеслера.
 ;
;
 для
стандартных условий
для
стандартных условий


приведенную температуру найдем
как
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
приведенное давление возьмем
из задания №7
 ацентрический фактор
ацентрический фактор
 возьмем из задания №3.
возьмем из задания №3.
-
Т
Т>r>
Δ>v>Z
Ψ
Δ>v>H0>T>
Δ>v>H>T>
298
0,64
0.9460
6.7911
25972.25
24570.50
323
0,70
0.9034
6.6247
25335.95
22889.08
348
0,75
0.8441
6.4918
24827.46
20957.11
373
0,80
0.7660
6.4073
24504.25
18769.98
398
0,86
0.6647
6.3912
24442.86
16247.15
423
0,91
0.5283
6.4698
24743.29
13072.03
448
0,97
0.3107
6.6765
25534.00
7932.90
Корреляция Риделя.
 ;
;

 для
стандартных условий
для
стандартных условий
 ,
,
R=8.314,
 -возьмем
из задания №3.,
-возьмем
из задания №3.,
 -Возьмем
из задания №7.,
-Возьмем
из задания №7.,
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
-
Т
Т>r>
Δ>v>Z
Ψ
Δ>v>H0>T>
Δ>v>H>T>
298
0,64
0.9349
6.3709
24365.00
22779.51
323
0,70
0.8888
6.2434
23877.57
21222.00
348
0,75
0.8267
6.1460
23505.06
19432.45
373
0,80
0.7471
6.0922
23299.16
17406.33
398
0,86
0.6458
6.0999
23328.70
15064.94
423
0,91
0.5114
6.1927
23683.60
12111.20
448
0,97
0.2996
6.4008
24479.36
7335.21
Корреляция Амброуза-Уолтона.
 ;
;

 для
стандартных условий
для
стандартных условий
 ;
;
приведенную температуру найдем
как
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
приведенное давление возьмем из задания №7
возьмем из задания №7
 ; ацентрический фактор
; ацентрический фактор
 возьмем из задания №3.
возьмем из задания №3.
|
Т |
Т>r> |
τ |
Δ>v>Z |
Ψ |
Δ>v>H0>T> |
Δ>v>H>T> |
|
298 |
0,64 |
0,36 |
0.9455 |
6.6994 |
25621.28 |
24225.72 |
|
323 |
0,70 |
0,30 |
0.9035 |
6.5651 |
25107.66 |
22683.59 |
|
348 |
0,75 |
0,25 |
0.8449 |
6.4710 |
24748.01 |
20908.85 |
|
373 |
0,80 |
0,20 |
0.7673 |
6.4196 |
24551.18 |
18837.55 |
|
398 |
0,86 |
0,14 |
0.6660 |
6.4175 |
24543.35 |
16346.30 |
|
423 |
0,91 |
0,09 |
0.5294 |
6.4834 |
24795.44 |
13127.15 |
|
448 |
0,97 |
0,03 |
0.3126 |
6.6832 |
25559.48 |
7990.55 |

о-Ксилол, 1,2-диметилбензол

Уравнение Ли-Кесслера.
 ;
;
 для
стандартных условий
для
стандартных условий


приведенную температуру найдем
как
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
приведенное давление возьмем
из задания №7
 ацентрический фактор
ацентрический фактор
 возьмем из задания №3.
возьмем из задания №3.
|
Т |
Т>r> |
Δ>v>Z |
Ψ |
Δ>v>H0>T> |
Δ>v>H>T> |
|
298 |
0,47 |
0.9990 |
8.4224 |
44128.95 |
44084.59 |
|
323 |
0,51 |
0.9969 |
8.2108 |
43020.40 |
42887.73 |
|
348 |
0,55 |
0.9923 |
8.0036 |
41934.58 |
41611.58 |
|
373 |
0,59 |
0.9836 |
7.8026 |
40881.71 |
40211.27 |
|
398 |
0,63 |
0.9692 |
7.6106 |
39875.39 |
38646.73 |
|
423 |
0,67 |
0.9475 |
7.4308 |
38933.42 |
36890.91 |
|
448 |
0,71 |
0.9174 |
7.2676 |
38078.62 |
34932.02 |
|
473 |
0,75 |
0.8776 |
7.1266 |
37339.93 |
32768.42 |
|
498 |
0,79 |
0.8270 |
7.0147 |
36753.48 |
30396.28 |
|
523 |
0,83 |
0.7642 |
6.9404 |
36363.89 |
27788.55 |
|
548 |
0,87 |
0.6862 |
6.9140 |
36225.70 |
24858.07 |
Корреляция Риделя.
 ;
;

 для
стандартных условий
для
стандартных условий
 ,
,
R=8.314,
 -возьмем
из задания №3.,
-возьмем
из задания №3.,
 -Возьмем
из задания №7.,
-Возьмем
из задания №7.,
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
|
Т |
Т>r> |
Δ>v>Z |
Ψ |
Δ>v>H0>T> |
Δ>v>H>T> |
|
298 |
0,47 |
0.9988 |
8.2268 |
43103.92 |
43053.96 |
|
323 |
0,51 |
0.9966 |
8.0303 |
42074.50 |
41929.42 |
|
348 |
0,55 |
0.9916 |
7.8380 |
41067.03 |
40721.80 |
|
373 |
0,59 |
0.9824 |
7.6518 |
40091.38 |
39387.30 |
|
398 |
0,63 |
0.9675 |
7.4742 |
39160.69 |
37887.72 |
|
423 |
0,67 |
0.9453 |
7.3084 |
38292.12 |
36197.77 |
|
448 |
0,71 |
0.9147 |
7.1587 |
37507.74 |
34306.49 |
|
473 |
0,75 |
0.8745 |
7.0304 |
36835.48 |
32211.93 |
|
498 |
0,79 |
0.8237 |
6.9301 |
36310.22 |
29908.93 |
|
523 |
0,83 |
0.7608 |
6.8661 |
35975.07 |
27368.73 |
|
548 |
0,87 |
0.6829 |
6.8485 |
35882.68 |
24503.06 |
Корреляция Амброуза-Уолтона.
 ;
;

 для
стандартных условий
для
стандартных условий
 ;
;
приведенную температуру найдем
как
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
приведенное давление возьмем из задания №7
возьмем из задания №7
 ; ацентрический фактор
; ацентрический фактор
 возьмем из задания №3.
возьмем из задания №3.
|
Т |
Т>r> |
τ |
Δ>v>Z |
Ψ |
Δ>v>H0>T> |
Δ>v>H>T> |
|
298 |
0,47 |
0,53 |
0.9989 |
8.3992 |
44007.33 |
43960.34 |
|
323 |
0,51 |
0,49 |
0.9967 |
8.1381 |
42639.19 |
42500.60 |
|
348 |
0,55 |
0,45 |
0.9920 |
7.9007 |
41395.59 |
41063.71 |
|
373 |
0,59 |
0,41 |
0.9832 |
7.6882 |
40281.95 |
39603.43 |
|
398 |
0,63 |
0,37 |
0.9687 |
7.5009 |
39301.06 |
38072.10 |
|
423 |
0,67 |
0,33 |
0.9473 |
7.3393 |
38454.18 |
36426.42 |
|
448 |
0,71 |
0,29 |
0.9175 |
7.2035 |
37742.41 |
34628.59 |
|
473 |
0,75 |
0,25 |
0.8782 |
7.0939 |
37168.29 |
32642.88 |
|
498 |
0,79 |
0,21 |
0.8282 |
7.0118 |
36738.00 |
30427.91 |
|
523 |
0,83 |
0,17 |
0.7658 |
6.9596 |
36464.79 |
27923.18 |
|
548 |
0,87 |
0,13 |
0.6879 |
6.9425 |
36375.17 |
25022.68 |

4-Метилпиридин

Уравнение Ли-Кеслера.
 ;
;
 для стандартных условий
для стандартных условий


приведенную температуру найдем
как
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
приведенное давление возьмем
из задания №7
 ацентрический фактор
ацентрический фактор
 возьмем из задания №3.
возьмем из задания №3.
|
Т |
Т>r> |
Δ>v>Z |
Ψ |
Δ>v>H0>T> |
Δ>v>H>T> |
|
298 |
0,46 |
0,9990 |
8,1297 |
44041,37 |
43998,94 |
|
323 |
0,50 |
0,9970 |
7,9439 |
43034,54 |
42906,26 |
|
348 |
0,53 |
0,9925 |
7,7613 |
42045,26 |
41729,02 |
|
373 |
0,57 |
0,9838 |
7,5834 |
41081,43 |
40416,16 |
|
398 |
0,61 |
0,9692 |
7,4121 |
40153,58 |
38918,11 |
|
423 |
0,65 |
0,9471 |
7,2500 |
39275,42 |
37196,66 |
|
448 |
0,69 |
0,9159 |
7,1003 |
38464,63 |
35230,47 |
|
473 |
0,73 |
0,8747 |
6,9672 |
37743,52 |
33014,65 |
|
498 |
0,76 |
0,8227 |
6,8558 |
37140,03 |
30554,58 |
|
523 |
0,80 |
0,7592 |
6,7725 |
36688,63 |
27854,70 |
|
548 |
0,84 |
0,6835 |
6,7250 |
36431,44 |
24901,06 |
|
573 |
0,88 |
0,5940 |
6,7228 |
36419,47 |
21632,00 |
|
598 |
0,92 |
0,4869 |
6,7771 |
36713,89 |
17874,28 |
|
623 |
0,96 |
0,3513 |
6,9015 |
37387,53 |
13132,81 |
Корреляция Риделя.
 ;
;

 для
стандартных условий
для
стандартных условий
 ,
,
R=8.314,
 - возьмем из задания №3,
- возьмем из задания №3,
 -
возьмем из задания №7,
-
возьмем из задания №7,
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
|
Т |
Т>r> |
Δ>v>Z |
Ψ |
Δ>v>H0>T> |
Δ>v>H>T> |
|
0.9991 |
8.1423 |
43731.22 |
43691.21 |
0.9991 |
8.1423 |
|
0.9972 |
7.9571 |
42736.09 |
42617.45 |
0.9972 |
7.9571 |
|
0.9931 |
7.7752 |
41759.48 |
41471.78 |
0.9931 |
7.7752 |
|
0.9854 |
7.5984 |
40809.69 |
40213.09 |
0.9854 |
7.5984 |
|
0.9726 |
7.4286 |
39897.81 |
38803.37 |
0.9726 |
7.4286 |
|
0.9533 |
7.2686 |
39038.32 |
37215.24 |
0.9533 |
7.2686 |
|
0.9264 |
7.1218 |
38249.81 |
35434.93 |
0.9264 |
7.1218 |
|
0.8909 |
6.9925 |
37555.85 |
33459.45 |
0.8909 |
6.9925 |
|
0.8459 |
6.8864 |
36985.84 |
31288.10 |
0.8459 |
6.8864 |
|
0.7904 |
6.8101 |
36576.13 |
28908.00 |
0.7904 |
6.8101 |
|
0.7223 |
6.7720 |
36371.13 |
26270.28 |
0.7223 |
6.7720 |
|
0.6382 |
6.7819 |
36424.57 |
23245.31 |
0.6382 |
6.7819 |
|
0.5302 |
6.8520 |
36800.95 |
19513.59 |
0.5302 |
6.8520 |
|
0.3768 |
6.9965 |
37577.02 |
14160.70 |
0.3768 |
6.9965 |
Корреляция Амброуза-Уолтона.
 ;
;

 для
стандартных условий
для
стандартных условий
 ;
;
приведенную температуру найдем
как
 ,
в интервале от 298К до
,
в интервале от 298К до
 .
.
приведенное давление возьмем из задания №7
возьмем из задания №7
 ; ацентрический фактор
; ацентрический фактор
 возьмем из задания №3.
возьмем из задания №3.
|
Т |
Т>r> |
τ |
Δ>v>Z |
Ψ |
Δ>v>H0>T> |
Δ>v>H>T> |
|
298 |
0,46 |
0,54 |
0.9989 |
8.0504 |
43237.49 |
43191.58 |
|
323 |
0,50 |
0,50 |
0.9968 |
7.8170 |
41983.98 |
41851.28 |
|
348 |
0,53 |
0,47 |
0.9923 |
7.6044 |
40842.07 |
40528.80 |
|
373 |
0,57 |
0,43 |
0.9841 |
7.4136 |
39817.23 |
39183.29 |
|
398 |
0,61 |
0,39 |
0.9707 |
7.2451 |
38912.35 |
37772.73 |
|
423 |
0,65 |
0,35 |
0.9510 |
7.0992 |
38128.67 |
36259.23 |
|
448 |
0,69 |
0,31 |
0.9238 |
6.9760 |
37466.76 |
34610.24 |
|
473 |
0,73 |
0,27 |
0.8881 |
6.8756 |
36927.82 |
32796.19 |
|
498 |
0,76 |
0,24 |
0.8431 |
6.7988 |
36515.22 |
30785.06 |
|
523 |
0,80 |
0,20 |
0.7874 |
6.7470 |
36236.83 |
28533.37 |
|
548 |
0,84 |
0,16 |
0.7192 |
6.7231 |
36108.80 |
25970.42 |
|
573 |
0,88 |
0,12 |
0.6350 |
6.7332 |
36163.09 |
22964.78 |
|
598 |
0,92 |
0,08 |
0.5274 |
6.7897 |
36466.43 |
19232.93 |
|
623 |
0,96 |
0,04 |
0.3755 |
6.9249 |
37192.43 |
13966.60 |

Задание №9
Для первого вещества рекомендованными методами рассчитать вязкость вещества при Т=730К и низком давлении.
Теоретический расчет:

где
 - вязкость при низком давлении; М -
молярная масса; Т - температура;
- вязкость при низком давлении; М -
молярная масса; Т - температура;
 -интеграл столкновений;
-интеграл столкновений;
 диаметр.
диаметр.

где характеристическая температура
 где
где
 -
постоянная Больцмана;
-
постоянная Больцмана;
 -
энергетический параметр; A=1.16145;B=0.14874;
C=0.52487;
D=077320;
E=2.16178;
F=2.43787.
-
энергетический параметр; A=1.16145;B=0.14874;
C=0.52487;
D=077320;
E=2.16178;
F=2.43787.
 где
где
 -
ацентрический фактор;
-
ацентрический фактор;
 и
и
 -возьмем из предыдущих заданий.
-возьмем из предыдущих заданий.

2-Метил-3,3-диэтилпентан

 ;
;
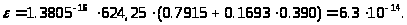 ;
;



Метод Голубева.
Т.к. приведенная температура
 то используем формулу:
то используем формулу:

где
 где
где
 -
молярная масса, критическое давление
и критическая температура соответственно.
-
молярная масса, критическое давление
и критическая температура соответственно.

 мкП.
мкП.
Метод Тодоса.

где

 -критическая
температура, критическое давление,
молярная масса соответственно.
-критическая
температура, критическое давление,
молярная масса соответственно.


Задание №10
Для первого соединения рассчитать рекомендованными методами вязкость вешества при температуре 730К. и давлении 100атм.
2-Метил-3,3-диэтилпентан

Расчет, основанный на понятии остаточной вязкости.

где
 -
вязкость плотного газа мкП;
-
вязкость плотного газа мкП;
 - вязкость при низком давлении мкП;
- вязкость при низком давлении мкП;
 -
приведенная плотность газа;
-
приведенная плотность газа;




Задание №11
Для первого вещества рекомендованными методами рассчитать теплопроводность вещества при температуре 730К и низком давлении.
Теплопроводность индивидуальных газов при низких давлениях рассчитывается по:
Корреляции Эйкена;
Модифицированной корреляции Эйкена и по корреляции Мисика-Тодоса.
Корреляция Эйкена.

где
 взято из задания №9; М=142,29 г/моль молярная
масса вещества;
взято из задания №9; М=142,29 г/моль молярная
масса вещества;
 -
изобарная теплоемкость; R=1,987.
-
изобарная теплоемкость; R=1,987.

 ;
;

Модифицированная корреляция Эйкена.

где
 взято из задания №9; М=142,29 г/моль молярная
масса вещества;
взято из задания №9; М=142,29 г/моль молярная
масса вещества;
 -
изобарная теплоемкость; R=1,987.
-
изобарная теплоемкость; R=1,987.

 ;
;

Корреляция Мисика-Тодоса.

где

 - критическая температура давление и
молярная масса соответственно;
- критическая температура давление и
молярная масса соответственно;
 теплоемкость вещества при стандартных
условиях;
теплоемкость вещества при стандартных
условиях;
 -
приведенная температура.
-
приведенная температура.


Задание №12
Для первого соединения рассчитать рекомендованными методами теплопроводность вещества при температуре 730К и давлении 100 атм.
2-Метил-3,3-диэтилпентан

 ,
выбираем уравнение:
,
выбираем уравнение:



Где
 - критическая температура давление
объем и молярная масса соответственно.
- критическая температура давление
объем и молярная масса соответственно.
 ,
,
 ,
,
 .
.