Магнітне поле у вакуумі
РЕФЕРАТ
на тему:”МАГНІТНЕ ПОЛЕ У ВАКУУМІ”
План
1. Магнітне поле. Магнітна індукція. Закон Ампера.
2. Закон Біо-Савара-Лапласа та його використання в найпростіших випадках:
а) Магнітне поле прямолінійного провідника із струмом;
б) Магнітне поле кругового провідника із струмом;
в) Магнітне поле соленоїда.
Магнітний момент контуру із струмом.
1. Магнітне поле. Магнітна індукція. Закон Ампера
Дослідним шляхом установлено, що подібно до електричних зарядів, навколо яких виникає електричне поле, в просторі навколо провідників із струмом або постійних магнітів виникає магнітне поле. Магнітне поле – це одна із форм існування матерії, завдяки якій здійснюється взаємодія струмів і постійних магнітів.
Встановлено також, що:
- магнітне поле діє лише на рухомі електричні заряди;
- рухомі електричні заряди створюють у просторі магнітне поле;
- магнітне поле не діє на статичні заряди.
Характер дії магнітного поля на струм залежить:
- від форми провідника, по якому тече струм;
- від розміщення провідника в просторі.
У якості пробного тіла для дослідження магнітного поля використовують замкнутий пробний контур з струмом, лінійні розміри якого досить малі. Магнітне поле такого пробного контуру не повинно створювати зовнішнього магнітного поля. При розміщенні такої рамки у досліджуване зовнішнє магнітне поле, із сторони останнього, на рамку діятиме обертальний момент сил М. Елементарна рамка із струмом займе певний напрям у просторі так, щоб магнітне поле рамки і досліджуваного магнітного поля збігалися (рис 11.1).

Рис11.1
Орієнтація контуру в просторі
характеризується напрямком нормалі
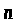 до контуру.
до контуру.
Додатний напрям нормалі визначається правилом правого гвинта. За позитивний напрям нормалі приймається напрям поступального руху правого гвинта, обертання якого збігаються з напрямком струму в пробній рамці.
За напрям магнітного поля у даній точці простору приймається напрям, вздовж якого направляється позитивно орієнтована нормаль до контуру.
Момент сил, який створюється зовнішнім магнітним полем у рамці із струмом, визначається векторним добутком вектора магнітного моменту рамки із струмом і магнітної індукції зовнішнього магнітного поля
 ,
(11.1.1)
,
(11.1.1)
де
 - магнітний момент пробної рамки із
струмом I і площею
S;
- магнітний момент пробної рамки із
струмом I і площею
S;
 - вектор магнітної індукції – силова
характеристика зовнішнього магнітного
поля.
- вектор магнітної індукції – силова
характеристика зовнішнього магнітного
поля.
Скалярна величина вектора моменту
сили
 визначається формулою
визначається формулою
 .
(11.1.2)
.
(11.1.2)
Якщо в дану точку зовнішнього
магнітного поля розміщувати елементарні
рамки із різними магнітними моментами
 ,
то на них з сторони магнітного поля
будуть діяти різні обертальні механічні
моменти сил
,
то на них з сторони магнітного поля
будуть діяти різні обертальні механічні
моменти сил
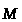 .
Однак відношення
.
Однак відношення
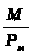 для кожного випадку буде сталою величиною,
яка є силовою характеристикою цього
поля. Позначають цю величину буквою
для кожного випадку буде сталою величиною,
яка є силовою характеристикою цього
поля. Позначають цю величину буквою
 і називають індукцією
магнітного поля.
і називають індукцією
магнітного поля.
 .
(11.1.3)
.
(11.1.3)
Індукція магнітного поля вимірюється у теслах (Тл), розмірність якого визначається з (11.1.3)
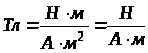 .
.
Подібно до електричного поля
магнітне поле зображають з допомогою
силових ліній магнітного поля, напрям
яких у кожній точці поля збігається із
напрямком вектора
 .
.
Лінії індукції магнітного поля завжди замкнуті й охоплюють провідники із струмом. Замкнутість силових ліній магнітного поля характеризує вихровий характер цього поля.
Природа магнітного поля зводиться або до руху електричних зарядів, або до змінного в часі електричного поля. Про це свідчать рівняння Максвела:
а)
 ,
(11.1.4)
,
(11.1.4)
де
 - циркуляція вектора електростатичного
поля вздовж довільного замкнутого
контуру;
- циркуляція вектора електростатичного
поля вздовж довільного замкнутого
контуру; 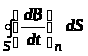 - потік змінного в часі вихрового
магнітного поля крізь довільну замкнуту
поверхню;
- потік змінного в часі вихрового
магнітного поля крізь довільну замкнуту
поверхню;
б)
 ,
(11.1.5)
,
(11.1.5)
де
 - струм провідності, який створюється
в провіднику вільними електричними
зарядами;
- струм провідності, який створюється
в провіднику вільними електричними
зарядами;
 - потік змінного в часі електричного
поля, що інколи називають струмом
зміщення. Струм зміщення не пов’язаний
з рухом будь-яких електричних зарядів.
- потік змінного в часі електричного
поля, що інколи називають струмом
зміщення. Струм зміщення не пов’язаний
з рухом будь-яких електричних зарядів.
Рівняння Максвелла (11.1.4) і (11.1.5) характеризують взаємозв’язок електричних і магнітних явищ. З рівняння (11.1.4) чітко видно, що змінне в часі магнітне поле є причиною виникнення вихрового електричного поля. Останнє, створює електричний струм у замкнутому провіднику.
З рівняння (11.1.5) випливає, що причиною виникнення магнітного поля може бути або струм провідності, або змінне в часі електричне поле, яке не обов’язково призводить до руху зарядів у провіднику.
Оскільки будь-який струм є причиною виникнення магнітного поля, то це пояснює дослідний факт силової дії магнітного поля на провідник із струмом.
Величину цієї сили знайшов Ампер, тому вона називається силою Ампера
 ,
(11.1.6)
,
(11.1.6)
де
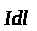 -
вектор елементу струму, що збігається
з напрямком струму у провіднику;
-
вектор елементу струму, що збігається
з напрямком струму у провіднику;
 -
індукція зовнішнього магнітного поля.
-
індукція зовнішнього магнітного поля.

Рис.11.2
На рис.11.2 струм створюється позитивними зарядами, напрям руху яких збігається з напрямком струму.
Напрям сили Ампера визначається правилом лівої руки. Якщо силові лінії магнітного поля входять в долоню лівої руки, а чотири пальці направлені по напрямку струму у провіднику, то великий палець, відхилений на 900, покаже напрямок сили Ампера.
2. Закон Біо-Савара-Лапласа та його використання у найпростіших випадках
Ще на початку 19-го сторіччя французькі фізики Біо і Савар, обробляючи величезний експериментальний матеріал вивчення характеристик магнітного поля провідників зі струмом за участю математика Лапласа, одержали формулу, яка дістала назву у фізиці закону Біо-Савара-Лапласа.
У векторній формі цей закон має вигляд
 ,
(11.2.1)
,
(11.2.1)
де - відносна магнітна проникність
середовища, безрозмірна величина; >о>
– магнітна постійна ( );
I – струм у провіднику;
);
I – струм у провіднику;
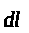 -
елемент провідника;
-
елемент провідника;
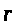 -
відстань від елемента струму до точки,
в якій знаходиться індукція магнітного
поля
-
відстань від елемента струму до точки,
в якій знаходиться індукція магнітного
поля
 (рис.11.3).
(рис.11.3).

Рис.11.3
З видно, що вектор індукції
магнітного поля
 є дотичною до силової лінії магнітного
поля, яка охоплює провідник, і проходить
через точку, в якій визначається індукція
магнітного поля.
є дотичною до силової лінії магнітного
поля, яка охоплює провідник, і проходить
через точку, в якій визначається індукція
магнітного поля.
Напрям силової лінії визначається за допомогою правила правого гвинта, як це показано на рисунку.
Поряд із індукцією магнітного
поля
 магнітне поле характеризується
напруженістю
магнітне поле характеризується
напруженістю
 .
Ця величина не залежить від властивостей
середовища і дорівнює
.
Ця величина не залежить від властивостей
середовища і дорівнює
 .
(11.2.2)
.
(11.2.2)
Величина напруженості
магнітного поля входить в одне із рівнянь
Максвелла. Розмірність напруженості
 буде встановлена трохи пізніше.
буде встановлена трохи пізніше.
Закон Біо – Савара - Лапласа для напруженості магнітного поля Н має вигляд
 ,
(11.2.3)
,
(11.2.3)
або в скалярній формі
 .
(11.2.4)
.
(11.2.4)
Магнітному полю властивий принцип суперпозиції. Це означає, що поля від кількох джерел магнітного поля накладаються як вектори, тобто
 .
(11.2.5)
.
(11.2.5)
Знайдемо індукцію магнітного поля біля безмежного прямого провідника із струмом (рис.11.4).
Скористаємось законом Біо – Савара - Лапласа в скалярній формі
 ,
(11.2.6)
,
(11.2.6)
де кут - це кут між напрямком
елемента провідника із струмом
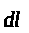 і радіусом-вектором
і радіусом-вектором
 ,
як це показано на рис.11.4;
,
як це показано на рис.11.4;
 - дотичний вектор до силової лінії,
напрям якого збігаються з напрямком
обертання правого гвинта.
- дотичний вектор до силової лінії,
напрям якого збігаються з напрямком
обертання правого гвинта.
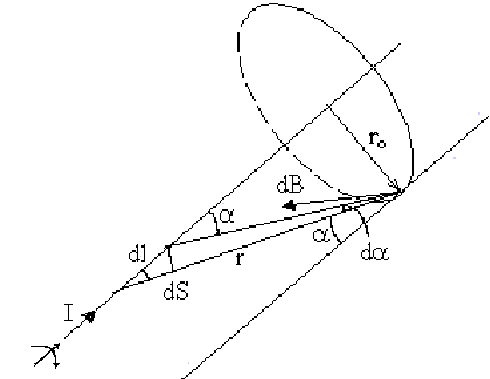
Рис.11.4
З рисунка видно, що
dS=dlsin і dS=rd,
звідки
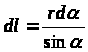 .
.
Радіус-вектор
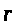 також можна виразити через r>o>
і кут , тобто
також можна виразити через r>o>
і кут , тобто
 .
.
З урахуванням цих зауважень закон Біо – Савара - Лапласа набуде вигляду
 .
(11.2.7)
.
(11.2.7)
Інтегруємо вираз (11.2.7) в межах зміни кута від >1> до >2>, в результаті чого одержимо
 .
(11.2.8)
.
(11.2.8)
Якщо у виразі (11.2.8) >1 >прямує до> >0, а >2 >прямує до , то одержимо безмежний прямий провідник із струмом.
У цьому випадку:
а) індукція магнітного поля буде дорівнювати
 . (11.2.9)
. (11.2.9)
б) напруженість магнітного поля буде дорівнювати
 .
(11.2.10)
.
(11.2.10)
З останньої формули легко встановити розмірність напруженості магнітного поля
 .
.
Знайдемо магнітне поле на осі кругового витка із струмом (рис.11.5).

Рис.11.5
Елемент провідника із струмом
dl, створює на осі
x індукцію магнітного
поля dB. Вектор
 є дотичним до силової лінії, зображеної
на рисунку пунктирною лінією. Складова
вектора індукції магнітного поля dB>y>
буде скомпенсована аналогічним елементом
з протилежної сторони. Результуючу
індукцію магнітного поля від кругового
витка із струмом слід шукати в напрямку
осі x (принцип
суперпозиції магнітних полів).
є дотичним до силової лінії, зображеної
на рисунку пунктирною лінією. Складова
вектора індукції магнітного поля dB>y>
буде скомпенсована аналогічним елементом
з протилежної сторони. Результуючу
індукцію магнітного поля від кругового
витка із струмом слід шукати в напрямку
осі x (принцип
суперпозиції магнітних полів).
З рисунка видно, що
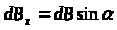 .
(11.2.11)
.
(11.2.11)
Закон Біо – Савара - Лапласа запишеться
 ,
(11.2.12)
,
(11.2.12)
тут враховано, що
 .
.
Підставимо вираз (11.2.12) у (11.2.11), одержимо
 .
(11.2.13)
.
(11.2.13)
Але врахувавши, що
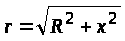 ;
і
;
і 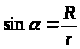 ,
,
одержимо
 .
(11.2.14)
.
(11.2.14)
Інтегруємо цей вираз в межах довжини витка від 0 до 2πR, одержимо
 .
.
Таким чином, магнітна індукція на осі кругового витка дорівнює визначається за допомогою формули
 .
(11.2.15)
.
(11.2.15)
Напруженість магнітного поля у цьому випадку буде дорівнювати
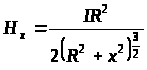 .
(11.2.16)
.
(11.2.16)
Для індукції та напруженості магнітного поля у центрі колового витка зі струмом одержимо
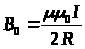 ,
(11.2.17)
,
(11.2.17)
 .
(11.2.18)
.
(11.2.18)
Знайдемо індукцію і напруженість магнітного поля на осі довгого соленоїда з струмом (рис.11.6).

Рис.11.6
Виділений елемент соленоїда шириною dx, в якому dN витків, що щільно прилягають один до одного, можна розглянути як круговий виток, індукція якого розраховується за формулою (11.2.15)
 ,
(11.2.19)
,
(11.2.19)
Кількість витків у виділеному елементі соленоїда дорівнює
dN = ndx,
де n – число витків на одиницю довжини соленоїда.
З урахуванням цих позначень одержуємо
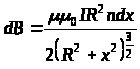 .
(11.2.20)
.
(11.2.20)
Виконаємо заміну змінних у співвідношенні (11.2.20), тобто
 ,
і
,
і  .
.
З урахуванням цих позначень одержимо, що
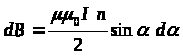 .
.
Інтегруємо цей вираз у межах зміни кута від >1> до >2>. Після інтегрування одержимо
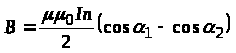 .
(11.2.21)
.
(11.2.21)
Якщо >1>0, а >2>, одержимо соленоїд безмежної довжини. У цьому випадку:
а) індукція магнітного поля на осі довгого соленоїда
 .
(11.2.22)
.
(11.2.22)
б) напруженість магнітного поля на осі довгого соленоїда
 .
(11.2.23)
.
(11.2.23)
3. Магнітний момент контуру із струмом
Для плоского контуру із струмом I магнітний момент визначається співвідношенням:
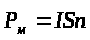 ,
(11.3.1)
,
(11.3.1)
де I – струм
у контурі; S – площа контуру;
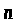 - нормаль до площини контуру, яка
збігається з поступальним рухом правого
гвинта, якщо його обертати за напрямком
струму у витку.
- нормаль до площини контуру, яка
збігається з поступальним рухом правого
гвинта, якщо його обертати за напрямком
струму у витку.

Рис.11.7
Якщо контур із струмом розмістити у зовнішнє магнітне поле, то результуюча сила Ампера, яка діє зі сторони зовнішнього магнітного поля на контур з струмом, буде дорівнювати нулю, тобто
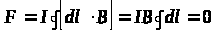 .
.
У випадку неоднорідного магнітного поля результуючий вектор сили Ампера не буде дорівнювати нулю.
Відповідні розрахунки показують, що в цьому випадку
 (11.3.2)
(11.3.2)
де
 - похідна вектора
- похідна вектора
 в напрямку нормалі або градієнт вектора
в напрямку нормалі або градієнт вектора
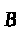 в напрямку нормалі до контуру;
в напрямку нормалі до контуру;
 - магнітний момент контуру.
- магнітний момент контуру.