Магнітне поле в речовині
РЕФЕРАТ
на тему:”МАГНІТНЕ ПОЛЕ В РЕЧОВИНІ”
План
1. Струми і механізм намагнічування. Намагнічуваність речовини.
2. Магнітна сприйнятливість і проникність.
3. Циркуляція намагнічування. Вектор напруженості магнітного поля.
4. Феромагнетики та їх основні властивості.
1. Струми і механізм намагнічування. Намагнічуваність речовини
Розглянемо орбітальний рух
електрона в атомі. Цей рух подібний до
деякого колового струму, який називають
мікрострумом. Мікрострум утворює в
просторі магнітне поле, яке можна
характеризувати за допомогою вектора
магнітного моменту
.
Розглянемо орбітальний рух електрона
(рис. 1).
Рис. 1
Струм і направлений у протилежну сторону орбітального руху електрона. Напрям магнітного моменту збігається з поступальним рухом правого гвинта, якщо його обертати за напрямком струму.
За означенням орбітальний магнітний момент визначається за формулою:
,
(1.1)
де і –
коловий струм; S - площа колового струму;
- нормаль до контуру з напрямком
поступального руху правого гвинта.
Величину колового струму оцінимо за формулою
,
(1.2)
де q>o>- заряд електрона; Т – період обертання електрона навколо ядра.
З рисунка видно, що
;
;
.
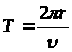З урахуванням цих зауважень одержимо:
. (1.3)
У випадку атома, в якому є z електронів, сумарний магнітний момент всіх z електронів буде дорівнювати:
(1.4)
2. Внесемо такий атом у змінне зовнішнє магнітне поле, величина якого змінюється від 0 до В протягом часу dt.
Змінне магнітне поле породжує у просторі вихрове електричне поле, величина якого описується рівнянням Максвелла
,
(1.5)
де
- змінне в часі магнітне поле; dS – площа
контуру вздовж якого рухається електрон;
Е – напруженість вихрового електричного
поля, породжена зміною магнітного поля.
Вихрове електричне поле має напрям силових ліній, які збігаються з напрямком струму в контурі. Напрям замкнутих силових ліній електричного поля теж визначається правилом правого гвинта, тобто напрям силових ліній збігається з напрямом струму в контурі.
Однак у цьому випадку електрони рухаються в сторону, протилежну напрямку струму. Тому вихрове електричне поле гальмує рух цих електронів.
На електрон у вихровому електричному
полі діє електрична сила
,
напрям якої дотичний до силової лінії
в сторону мікроструму (рис.2).
Рис.2
Згідно з рівнянням (14.1.5) змінне в часі магнітне поле породжує вихрове електричне поле, струм якого згідно з правилом Ленца має бути протилежний до діючого мікроструму і.
Силові лінії вихрового електричного поля у випадку наростаючого магнітного поля мають такий напрям, щоб визваний ним струм індукції
протилежним до і,
а магнітний момент
такого струму теж був протилежний до
.
Розглянемо цей випадок трохи детальніше. Скористаємось другим законом Ньютона
,
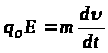(1.6)
де
- електрична сила індукована змінним в
часі магнітним полем; m
– маса електрона;
- прискорення гальмування.
З рівняння (14.1.6) прискорення руху електрона дорівнює
.
(1.7)
Напруженість вихрового електричного поля Е знайдемо з рівняння Максвелла (14.1.5)
,
де
,
а
,
тому
,
звідки
.
Тому
,
або
.
Інтегруємо останній вираз у межах зміни швидкості від >о> до> >, а індукції магнітного поля від 0 до В
.
Після інтегрування одержимо:
.
(1.8)
Значення швидкості з (14.1.8) підставимо у вираз орбітального магнітного моменту (14.1.3)
.
(1.9)
Для атома, в якому є z електронів, одержимо:
,
(1.10)
де
- складова, яка пов’язана з орбітальним
рухом електрона в атомі;
- складова, яка появляється лише у
зовнішньому магнітному полі.
Одержана формула (14.1.10) показує, що магнітний момент атома у випадку дії змінного в часі магнітного поля зменшується за рахунок намагнічування атома у протилежному напрямі.
Магнетики, для яких характерна ця особливість, називаються діамагнетиками.
Покажемо, що у випадку, коли
не збігається з напрямком дії змінного
в часі магнітного поля, такі атоми
здійснюють прецесію. Частота цієї
прецесії дорівнює
;
але
,
тому
,
де
.
Величину
- називають гіромагнітним відношенням,
а
- Ларморова частота прецесії.
Рис.3
2. Магнітна сприйнятливість і проникність
Якщо магнетики намагнічуються
у ту ж сторону, що і
,
то вони називаються парамагнетиками.
Кількісною мірою намагнічування є вектор намагніченості, який можна подати через одиницю об’єму речовини:
,
(2.1)
де n
– концентрація атомів або їх число в
одиниці об’єму магнетика;
- індукований магнітний момент атома,
друга складова у рівнянні (1.10).
З урахуванням викладеного одержуємо
,
або
.
(2.2)
Величину
називають магнітною сприйнятли-вістю.
Якщо магнітна сприйнятливість <0, то такі магнетики називають діамагнетиками.
За розрахунками Кюрі-Венса для парамагнетиків
.
У цьому випадку магнітна сприйнятливість обернено пропорційна до абсолютної температури.
З інших міркувань встановлено, що
,
(2.3)
де - відносна магнітна проникність середовища; - магнітна сприйнятливість.
Із співвідношення (14.2.3) одержуємо:
> 1- парамагнетики; < 1 - діамагнетики.
Прикладом діамагнітних речовин є металевий вісмут. При внесенні шматочка вісмуту, підвішеного до нитки у зовнішнє магнітне поле, останнє цей шматочок виштовхує з магнітного поля.
Парамагнітна мідь або латунь слабо втягуються у зовнішнє магнітне поле.
3. Циркуляція намагнічування. Вектор напруженості магнітного поля
Нехай у деякому середовищі діє зовнішнє магнітне поле, напрям якого показаний на рис. 4
Рис.4
Замкнутий контур, показаний на рис.14.4, охоплює певну кількість атомних струмів і>k>, а також струм провідності І.
Знайдемо циркуляцію вектора
вздовж замкнутого контуру
,
(3.1)
де І – струм провідності;
- алгебраїчна сума всіх атомних струмів,
нанизаних на цей контур.
Виділимо об’єм Sdl, у якому міститься idN елементарних атомних струмів. У виділеному об’ємі
,
(3.2)
де j – вектор намагніченості магнетика.
З урахуванням (14.3.2) алгебраїчну суму всіх атомних струмів можна записати так:
. (3.3)
Закон повного струму (14.3.1) з урахуванням останніх зауважень буде мати вигляд:
;
(3.4)
або
, (3.5)
де
=Н
– напруженість магнітного поля.
З урахуванням цього позначення закон повного струму набуде вигляду:
(3.6)
Оскільки вектор намагнічування магнетика визначається через магнітну сприйнятливість і напруженість магнітного поля співвідно-шенням (14.2.2)
,
то індукція магнітного поля буде дорівнювати
,
або
.
(3.7)
Введемо позначення
,
тоді
,
Де
відносна магнітна проникність середовища;
>0> – магнітна
проникність вакууму.
Оскільки
,
а
,
то
. (14.3.8)
Графічно цю залежність виражають так:
Рис.5
Всі магнетики діляться на три групи, для яких:
- діамагнетики;
- парамагнетики;
>>0; >> 1 – феромагнетики.
4. Феромагнетики та їх основні властивості
Поряд із слабомагнітними речовинами діамагнетиками і парамагнетиками, існують сильно магнітні речовини - феромагнетики.
До феромагнетиків відносяться речовини, які мають від природи спонтанну намагніченість, тобто зберігають намагніченість при відсутності зовнішнього магнітного поля.
У діамагнетиках вектор намагніченості j лінійно змінюється із зростанням напруженості зовнішнього магнітного поля. У феромагнетиках при зростанні Н вектор j росте до насичення, а потім залишається постійним.
Магнітна проникність у феромагнетиках може досягати значень, які вимірюються сотнями тисяч одиниць.
Магнітна проникність і магнітна індукція у феромагнетиках залежить від величини напруженості зовнішнього магнітного поля. (рис.14.6)
Рис.6
Як видно з рис. 6 в слабих магнітних полях індукція магнітного поля з ростом Н зростає досить швидко. В сильних магнітних полях через властивості насичення, зростання індукції магнітного поля феромагнетика не спостерігається.
Класичну теорію феромагнетизму розробив французький фізик Вейсс. В основу цієї теорії він поклав дві гіпотези. Перша з них полягає в тому, що для феромагнетиків властиве спонтанне намагнічування лише в певній області температур (починається біля абсолютного нуля і закінчується температурою Кюрі), яке не залежить від наявності зовнішнього намагнічувального поля. Однак досліди показують, що у випадку відсутності зовнішнього намагнічувального поля будь-яке феромагнітне тіло в цілому буде розмагнічене. Наступна гіпотеза стверджує, що нижче температури Кюрі будь-яке феромагнітне тіло поділяється на малі області, для яких характерне однорідне спонтанне намагнічування. Такі області називаються доменами. Лінійні розміри домен не перевищують 0,1 мм.
При відсутності зовнішнього магнітного поля магнітні моменти окремих домен орієнтовані у просторі хаотично, так що сумарний магнітний момент всього феромагнетика дорівнює нулю. Зовнішнє магнітне поле, що діє на феромагнетик, орієнтує магнітні моменти не окремих атомів, як це було у парамагнетиків, а цілих областей спонтанного намагнічування. З цих міркувань зрозуміло, що магнітне насичення настає тоді, коли вектори магнітних моментів всіх домен будуть встановлені паралельно до напрямку зовнішнього магнітного поля.
Для феромагнетиків властива така особливість намагнічування, як магнітний гістерезис (рис.14.7).
Рис.7
Нехай намагнічування феромагнетика до насичення (точка 1 на рис. 14.7) відбувається по кривій 01. Якщо далі зменшувати напруженість Н зовнішнього намагнічувального поля, то як показує дослід, розмагнічування феромагнетика відбуватиметься за кривою 1-2, розміщеної вище кривої намагнічування. Якщо напруженість намагнічувального поля досягне нуля Н=0, у феромагнетику спостерігається деяке залишкове намагнічування І>з>, обумовлене тим, що і після припинення дії зовнішнього магнітного поля в частині доменів зберігається переважна орієнтація їхніх магнітних моментів. Щоб повністю розмагнітити даний зразок феромагнетика, треба створити намагнічувальне поле Н>к> у протилежному напрямку. Величину цього поля Н>к >називають коерцитивною силою. При дальшому збільшенні зовнішнього поля у протилежному напрямку, намагнічування зразка знову досягне насичення у точці 4. Повертаючись поступово до початкового намагнічування, дістанемо замкнуту криву, яка називається петлею гістерезису.
Залишкова намагніченість І>з>> >і коерцитивна сила Н>к> характеризують властивість феромагнетика намагнічуватись і зберігати це намагнічування для тих чи інших практичних цілей.
При намагнічуванні феромагнетика відбувається зміна його форми і об’єму. Це явище називають магнітострикцією, яке було відкрите Джоулем ще в середині 19 століття.
Сучасна теорія феромагнетизму була розроблена на початку минулого століття. Відповідальними за діамагнітні властивості феромагнетиків є власні магнітні моменти електронів (спінові магнітні моменти). При певних умовах в кристалах виникають так звані обмінні сили, які примушують магнітні моменти електронів встановлюватись паралельно один одному, внаслідок чого і виникають області спонтанного намагнічування – домени.
Природа феромагнетизму має квантове пояснення. За магнітні властивості феромагнетиків несуть відповідальність електрони недобудованих 3-d - оболонок феромагнетиків. В цих оболонках частина електронів мають не скомпенсовані спіни. Спін електрона – це невіддільна квантова властивість електрона. Тому природа феромагнетизму є спінова.
Площа петлі гістерезису чисельно дорівнює роботі перемагнічування. Чим менша площа петлі, тим менше енергії витрачається на перемагнічування феромагнетика.
Далі наведено приклади петлі гістерезису для різних типів феромагнетиків:
а)магнітожорсткий б) магнітом’який в) феромагнетик феромагнетик; феромагнетик; із незадовільними магнітними властивостями
Для кожного феромагнетика є своя температура, яку називають температурою Кюрі. При температурі Кюрі феромагнетик втрачає магнітні властивості і перетворюється у парамагнетик. При цій температурі зникають області спонтанного намагнічування, які називають доменами.