Кинематический и силовой расчет механизма (работа 1)
Курсовая работа
Кинематический и силовой расчет механизма
Калуга
Рассмотрим структурную схему вытяжного
пресса. Вытяжной пресс – вертикальный
кривошипный пресс, предназначенный для
выполнения операций неглубокой вытяжки
с малым рабочим ходом. Рычажный механизм
станка состоит из кривошипа 1, шатуна
2, кулисы 3, вращающейся относительно
оси
 ,
шатуна 4 и ползуна 5. Ползун 5 совершает
возвратно-поступательное движение по
вертикальным направляющим стойки.
Вытяжка (рабочий ход) осуществляется
при движении ползуна вниз, навстречу
заданной силе сопротивления F.
,
шатуна 4 и ползуна 5. Ползун 5 совершает
возвратно-поступательное движение по
вертикальным направляющим стойки.
Вытяжка (рабочий ход) осуществляется
при движении ползуна вниз, навстречу
заданной силе сопротивления F.
Структурный анализ механизма
Определим число степеней свободы механизма по формуле Чебышева:
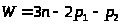
где
 – число подвижных звеньев механизма,
– число подвижных звеньев механизма,
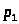 – число низших кинематических пар,
– число низших кинематических пар,
 – число высших кинематических пар.
– число высших кинематических пар.
Согласно структурной схеме механизма:
число
подвижных звеньев
 ,
,
количество
низших кинематических пар
 .
.
-
0 – 1
1 - 2
2 – 3
3 – 0
3 – 4
4 – 5
5 – 0
В
В
В
В
В
В
П
Здесь В - вращательная кинематическая пара,
П – поступательная кинематическая пара.
Количество высших кинематических пар:
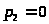 .
.

Механизм имеет одну степень свободы, и значит, в нем должно быть одно начальное звено. За начальное звено принимаем кривошип 1, движение которого задано, на котором требуется определить уравновешивающую силу.
Последовательность образования механизма по Ассуру:
Начальное звено 1 + стойка 0.
Возможными поводками (звеньями) для присоединения групп Ассура к начальному звену и стойке являются звенья: 2, 3, 5 (звенья, образующие кинематические пары со звеньями 1 и 0). Из них звенья 2 и 3 , соединенные между собой, образуют двухповодковую группу Ассура 1 вида (ВВВ). В этой группе внешние кинематические пары, которыми звенья группы присоединяются к начальному звену и стойке вращательные: (1 – 2) и (3 – 0), внутренняя кинематическая пара, которая соединяет между собой звенья 2 и 3 – также вращательная (2 – 3). Присоединив 2ПГ Ассура 1 вида к начальному звену 1 и стойке 0 , получим промежуточный механизм – 0, 1, 2, 3.
По отношению к промежуточному механизму поводками будут звенья 5 и 4 (образующие кинематические пары со звеньями промежуточного механизма). Звенья 4 и 5 образуют двухповодковую группу Ассура 2 вида (ВВП). В ней внешние кинематические пары: вращательная (3 – 4) и поступательная (5 – 0), внутренняя кинематическая пара – вращательная (4–5).
Таким образом, механизм вытяжного пресса образован последовательным присоединением к начальному звену 1 и стойке 0 двух двухповодковых групп Ассура - сначала 2ПГ 1 вида, а затем 2ПГ 2 вида.
Построение положений механизма
Для построения кинематической схемы
исследуемого механизма в различных
положениях выбираем масштабный
коэффициент длины
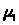 ,
который определяется как
,
который определяется как
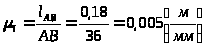
где
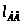 -
действительный радиус кривошипа в м;
-
действительный радиус кривошипа в м;
 –
радиус кривошипа на чертеже в мм.
–
радиус кривошипа на чертеже в мм.
Все требуемые положения механизма удобно строить на одном чертеже (т.е. с одним центром вращения кривошипа). На чертеже механизм показан в четырех положениях. Каждое положение обозначено соответствующим индексом:
 – соответствует нижнему крайнему
положению ползуна 5 (ведомого
– соответствует нижнему крайнему
положению ползуна 5 (ведомого
звена),
 –
соответствует верхнему крайнему
положению ползуна 5,
–
соответствует верхнему крайнему
положению ползуна 5,
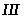 – соответствует холостому ходу ползуна
5 ,
– соответствует холостому ходу ползуна
5 ,
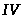 – соответствует рабочему ходу ползуна
5.
– соответствует рабочему ходу ползуна
5.
Крайние положения механизма соответствуют
крайним положениям коромысла 3 -
 и
и
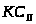 .
Эти положения получаются, когда кривошип
1 и шатун 2 располагаются на одной прямой,
соответственно вытягиваясь или
складываясь. Поэтому для определения
точки
.
Эти положения получаются, когда кривошип
1 и шатун 2 располагаются на одной прямой,
соответственно вытягиваясь или
складываясь. Поэтому для определения
точки
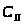 ,
радиусом
,
радиусом
 делаем засечку из точки
делаем засечку из точки
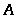 на дуге радиуса
на дуге радиуса
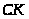 .
При этом точка
.
При этом точка
 займет положение
займет положение
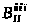 .
Точку
.
Точку
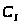 получим, делая засечку радиусом
получим, делая засечку радиусом
 из точки
из точки
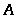 на дуге радиуса
на дуге радиуса
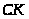 .
Точка
.
Точка
 займет положение
займет положение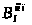 .
Рабочему ходу ползуна соответствует
угол поворота кривошипа
.
Рабочему ходу ползуна соответствует
угол поворота кривошипа
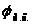 >,
>холостому ходу -
>,
>холостому ходу -
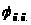
При выборе расчетного рабочего положения используем диаграмму сил
 ,
,
построенную на ходе ползуна 5. В вытяжном прессе процесс вытяжки происходит только на части рабочего хода, соответствующей

Поэтому выбираем положение кривошипа
на угле поворота
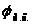 >,
>соответствующем рабочему ходу, когда
ползун 5 (точка
>,
>соответствующем рабочему ходу, когда
ползун 5 (точка
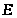 )
внутри этого отрезка.
)
внутри этого отрезка.
При выборе положения механизма,
соответствующего холостому ходу ползуна,
берем любое положение кривошипа на угле
его поворота
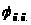 >.>
>.>
Построение планов скоростей и ускорений
Планы скоростей и ускорений требуется построить для трех положений механизма: для положений на рабочем и холостом ходах и для одного из крайних положений. Рассмотрим построение плана скоростей и ускорений для рабочего положения механизма.
Последовательность кинематического исследования определена последовательностью образования механизма:
начальное звено 1 и стойка 0;
двухповодковая группа Ассура 1 вида, состоящая из звеньев 2 и 3,
двухповодковая группа Ассура 2 вида, состоящая из звеньев 4 и 5.
Построение планов скоростей
Для начального звена 1 угловая скорость постоянна и равна:
 ,
,
где
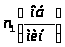 –
заданная частота вращения кривошипа.
–
заданная частота вращения кривошипа.
Скорость
точки
 начального звена равна
начального звена равна
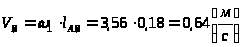 ,
,
вектор
скорости направлен перпендикулярно
звену
 в сторону, соответствующую направлению
угловой скорости
в сторону, соответствующую направлению
угловой скорости
 .
.
На
плане скоростей скорость точки
 изображается отрезком
изображается отрезком
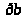 .
Масштабный коэффициент плана скоростей:
.
Масштабный коэффициент плана скоростей:
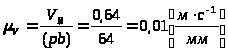 .
.
Для
точки
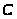 согласно первому способу разложения
движения:
согласно первому способу разложения
движения:
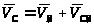 ,
,
где
 .
Поэтому через точку
.
Поэтому через точку
 проводим прямую, перпендикулярную
проводим прямую, перпендикулярную
 .
С другой стороны согласно первому
способу разложения движения:
.
С другой стороны согласно первому
способу разложения движения:
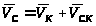 ,
,
где

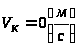 ,
т.к. точка закреплена, а
,
т.к. точка закреплена, а
 .
Поэтому через точку
.
Поэтому через точку
 ,
лежащую в полюсе
,
лежащую в полюсе
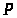 ,
проводим прямую, перпендикулярную
,
проводим прямую, перпендикулярную
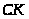 .
Точка пересечения этих прямых и есть
точка
.
Точка пересечения этих прямых и есть
точка
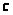 (стрелки ставим к этой точке).
(стрелки ставим к этой точке).
На
схеме механизма точка
 лежит на звене 2. Следовательно, и на
плане скоростей точка
лежит на звене 2. Следовательно, и на
плане скоростей точка
 будет лежать на отрезке
будет лежать на отрезке
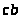 в соответствии с теоремой о подобии.
Отрезок
в соответствии с теоремой о подобии.
Отрезок
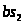 определяем
из пропорции:
определяем
из пропорции:
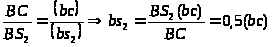
Так
как все абсолютные скорости выходят из
полюса, то соединяем точку
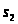 с
с
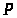 (стрелка к точке
(стрелка к точке
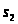 ).
).
На
схеме механизма точка
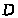 принадлежит кулисе 3. Следовательно,
и на плане скоростей точка
принадлежит кулисе 3. Следовательно,
и на плане скоростей точка
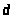 будет лежать на отрезке
будет лежать на отрезке
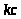 в соответствии с теоремой о подобии.
Отрезок
в соответствии с теоремой о подобии.
Отрезок
 определяем
из пропорции:
определяем
из пропорции:

или,
так как точка
 лежит в полюсе, то
лежит в полюсе, то

На
схеме механизма точка
 лежит на звене 3. Следовательно, и на
плане скоростей точка
лежит на звене 3. Следовательно, и на
плане скоростей точка
 будет лежать на отрезке
будет лежать на отрезке
 в соответствии с теоремой о подобии.
Отрезок
в соответствии с теоремой о подобии.
Отрезок
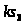 определяем
из пропорции:
определяем
из пропорции:
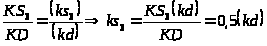
или,
так как точка
 лежит в полюсе, то
лежит в полюсе, то
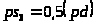
Далее
переходим ко второй группе Ассура,
включающей звенья 4 и 5. Для точки
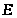 ,
согласно первому способу разложения
движения
,
согласно первому способу разложения
движения
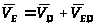 ,
,
где
 ,
т.к. точка
,
т.к. точка
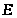 вместе с пятым звеном движется
поступательно по вертикали, а
вместе с пятым звеном движется
поступательно по вертикали, а
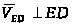 .
Поэтому через полюс
.
Поэтому через полюс
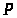 проводим прямую параллельную
проводим прямую параллельную
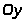 т.к. все абсолютные скорости выходят из
полюса, а через точку
т.к. все абсолютные скорости выходят из
полюса, а через точку
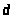 проводим прямую, перпендикулярную
проводим прямую, перпендикулярную
 .
Точка пересечения этих прямых есть
точка
.
Точка пересечения этих прямых есть
точка
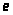 (стрелки ставим к этой точке).
(стрелки ставим к этой точке).
Так
как ползун 5 двигается поступательно,
то скорость центра масс ползуна
 .
.
Пользуясь построенным планом скоростей, можно определить угловые скорости звеньев:
 ,
,
 ,
,
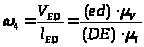 .
.
Для
определения направления
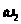 переносим вектор скорости
переносим вектор скорости
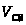 в точку
в точку
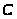 на схеме механизма и рассматриваем
движение точки
на схеме механизма и рассматриваем
движение точки
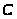 относительно точки
относительно точки
 в направлении скорости
в направлении скорости
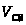 .
.
Для
определения направления
 переносим вектор скорости
переносим вектор скорости
 в точку
в точку
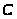 на схеме механизма и рассматриваем
вращение кулисы в направлении скорости
на схеме механизма и рассматриваем
вращение кулисы в направлении скорости
 .
.
Для
определения направления
 переносим вектор относительной скорости
переносим вектор относительной скорости
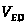 в точку
в точку
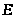 и рассматриваем движение точки
и рассматриваем движение точки
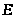 относительно точки
относительно точки
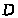 .
.
Результаты
построения планов скоростей для положений
механизма
 ,
,
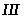 и
и
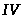 сведены в таблицу.
сведены в таблицу.
-
Положение механизма


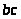
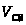

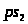

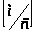

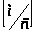


 – вкт
– вкт0
0
64
0,64
32
32
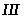 – х.х.
– х.х.
69,25
0,693
63,41
0,634
31,71
58,66
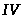 – р.х.
– р.х.32,28
0,323
51,78
0,518
25,89
43,57
-
Положение механизма
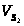

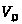
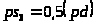
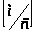

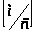

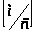
 – вкт
– вкт0,32
0
0
0
0
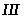 – х.х.
– х.х.
0,587
117,73
1,177
58,86
0,589
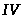 – р.х.
– р.х.0,436
54,87
0,549
27,43
0,274
-
Положение механизма
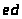
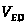
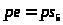

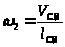
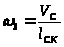


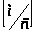

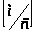



 – вкт
– вкт0
0
0
0
0,43
0
0
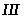 – х.х.
– х.х.
20,46
0,205
115,18
1,152
0,43
1,54
0,23
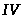 – р.х.
– р.х.19,63
0,196
51,12
0,511
0,35
0,72
0,22
Построение планов ускорений
Ускорение
точки
 равно нормальному ускорению при вращении
точки
равно нормальному ускорению при вращении
точки
 вокруг точки
вокруг точки
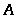
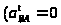 ,
т.к.
,
т.к.
 и направлено к центру вращения (от
и направлено к центру вращения (от
 к
к
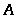 ):
):
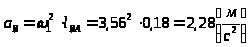 .
.
На
плане ускорений ускорение точки
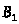 изображается отрезком
изображается отрезком
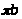 .
Масштабный коэффициент плана ускорений:
.
Масштабный коэффициент плана ускорений:
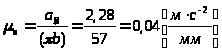 .
.
Векторные
равенства для нахождения ускорения
точки
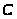 имеют
вид:
имеют
вид:
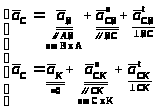
Нормальное
ускорение при вращении точки
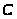 относительно точки
относительно точки
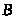
 направлено по звену
направлено по звену
 от точки
от точки
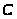 к точке
к точке
 ,
а отрезок, его изображающий, равен
,
а отрезок, его изображающий, равен
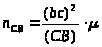
 ,
где
,
где

Нормальное
ускорение при вращении точки
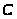 относительно точки
относительно точки

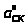 направлено по звену
направлено по звену
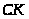 от точки
от точки
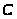 к точке
к точке
 ,
а отрезок, его изображающий, равен
,
а отрезок, его изображающий, равен

 .
.
Пересечение
перпендикуляров к звеньям
 и
и
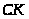 дадут точку
дадут точку
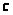 на плане ускорений (стрелки направлены
к этой точке).
на плане ускорений (стрелки направлены
к этой точке).
Так
как все абсолютные ускорения выходят
из полюса, то соединяем точку
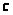 с
с
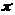 (стрелка к точке
(стрелка к точке
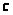 ).
).
Ускорение
точки
 шатуна 2 определяем согласно теореме
о подобии пропорциональным делением
одноименных отрезков на схеме механизма
и на плане ускорений.
шатуна 2 определяем согласно теореме
о подобии пропорциональным делением
одноименных отрезков на схеме механизма
и на плане ускорений.
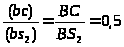 ;
откуда
;
откуда
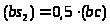 .
.
Так
как все абсолютные ускорения выходят
из полюса, то соединяем точку
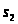 с
с
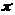 (стрелка к точке
(стрелка к точке
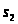 ).
).
На
схеме механизма точка
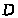 принадлежит кулисе 3. Следовательно, и
на плане ускорений
принадлежит кулисе 3. Следовательно, и
на плане ускорений
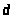 будет лежать на отрезке
будет лежать на отрезке
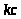 в соответствии с теоремой о подобии.
Отрезок
в соответствии с теоремой о подобии.
Отрезок
 определяем
из пропорции:
определяем
из пропорции:

или,
так как точка
 лежит в полюсе, то
лежит в полюсе, то
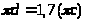
На
схеме механизма точка
 лежит на звене 3. Следовательно, и на
плане ускорений точка
лежит на звене 3. Следовательно, и на
плане ускорений точка
 будет лежать на отрезке
будет лежать на отрезке
 в соответствии с теоремой о подобии.
Отрезок
в соответствии с теоремой о подобии.
Отрезок
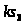 определяем
из пропорции:
определяем
из пропорции:
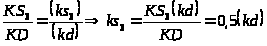
или,
так как точка
 лежит в полюсе, то
лежит в полюсе, то

Далее записываем векторное равенство для следующей 2ПГ 2-го вида, включающей звенья 4 и 5:
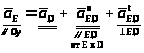
Нормальное
ускорение при вращении точки
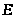 относительно точки
относительно точки
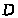 –
–
 направлено по звену
направлено по звену
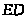 от точки
от точки
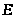 к точке
к точке
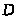 ,
при этом отрезок
,
при этом отрезок
 ,
изображающий на плане ускорений
нормальное ускорение при вращении точки
,
изображающий на плане ускорений
нормальное ускорение при вращении точки
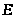 вокруг точки
вокруг точки
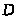 ,
равен
,
равен

 .
.
Так
как ползун 5 двигается поступательно,
то ускорение центра масс ползуна
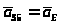 .
.
Пользуясь построенным планом ускорений, определим угловые ускорения звеньев:
 ;
;
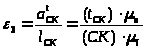 ;
;
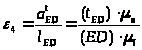 .
.
Для
определения направления углового
ускорения звена 2 переносим с плана
ускорений вектор тангенциального
ускорения
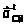 в точку
в точку
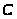 механизма (вращение относительно точки
механизма (вращение относительно точки
 ).
).
Для
определения направления углового
ускорения звена 3 переносим с плана
ускорений вектор тангенциального
ускорения
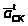 в точку
в точку
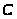 механизма (вращение относительно точки
механизма (вращение относительно точки
 ).
).
Для
определения направления углового
ускорения звена 4 переносим с плана
ускорений вектор тангенциального
ускорения
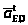 в точку
в точку
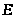 механизма (вращение относительно точки
механизма (вращение относительно точки
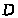 ).
).
Аналогично
построению планов скоростей результаты
построения планов ускорений для положений
механизма
 ,
,
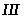 и
и
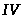 сведены в таблицу
сведены в таблицу
-
Положение механизма
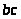

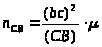
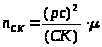

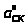






 – вкт
– вкт64
0
6,92
0
0,28
0
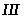 – х.х.
– х.х.
63,41
69,25
6,79
26,64
0,27
1,07
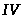 – р.х.
– р.х.51,78
32,28
4,53
5,79
0,18
0,23
-
Положение механизма
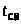

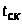


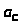






 – вкт
– вкт51,9
2,08
82,34
3,29
82,34
3,29
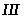 – х.х.
– х.х.
64,41
2,58
18,73
0,75
32,57
1,30
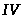 – р.х.
– р.х.27,76
1,11
44,43
1,78
44,8
1,79
-
Положение механизма
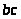
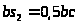
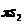
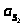
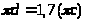







 – вкт
– вкт52,36
26,18
65,79
2,63
139,98
69,99
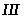 – х.х.
– х.х.
64,76
32,38
33,26
1,33
55,37
27,68
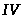 – р.х.
– р.х.28,13
14,07
49,3
1,97
76,16
38,08
-
Положение механизма
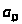

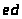











 – вкт
– вкт5,60
2,80
0
0
0
58,81
2,35
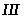 – х.х.
– х.х.
2,21
1,11
20,46
1,16
0,05
39,05
1,56
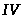 – р.х.
– р.х.3,05
1,52
19,63
1,07
0,04
17,82
0,71
-
Положение механизма
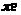
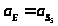

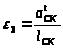
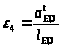





 – вкт
– вкт128,79
5,15
1,40
7,32
2,61
 – х.х.
– х.х.
39,51
1,58
1,74
1,66
1,74
 – р.х.
– р.х.75,01
3,00
0,75
3,95
0,79
Кинетостатический расчет механизма
Определение сил инерции звеньев
Для рассматриваемого механизма чеканочного пресса заданы:
массы
звеньев
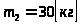 ,
,
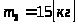 и
и
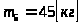 (массы звеньев 1 и 4 не учитываются);
(массы звеньев 1 и 4 не учитываются);
положения
центров масс звеньев – координаты
точек
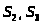 и
и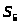 ;
;
моменты
инерции
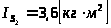 и
и
 .
.
При определении сил инерции и моментов сил инерции воспользуемся построенным планом ускорений для нахождения ускорений центров масс звеньев и угловых ускорений звеньев для рабочего хода механизма:
ускорения
центров масс
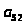 ,
,
 и
и
 возьмем из таблицы результатов:
возьмем из таблицы результатов:
 ,
,
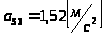 ,
,
 .
.
определение
угловых ускорений звеньев
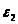 и
и
 также приведено при построении плана
ускорений:
также приведено при построении плана
ускорений:
 ,
,
 .
.
Теперь рассчитаем модули сил инерции:
звено 2 совершает плоскопараллельное движение:
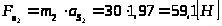 ;
;
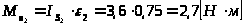 ;
;
звено 3 вращательное движение:
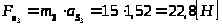 ;
;
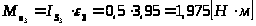 ;
;
звено 5 совершает поступательное движение вдоль неподвижной направляющей:
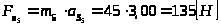 .
.
Силы
инерции
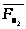 ,
,
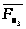 ,
,
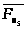 приложены в центрах масс
приложены в центрах масс
 ,
,
 звеньев и направлены противоположно
соответствующим ускорениям
звеньев и направлены противоположно
соответствующим ускорениям
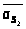 ,
,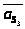 ,
,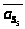 .
Моменты сил инерции
.
Моменты сил инерции
 и
и
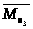 по направлениям противоположены
соответствующим угловым ускорениям
по направлениям противоположены
соответствующим угловым ускорениям
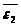 и
и
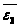 .
.
На
схеме механизма в рассматриваемом
рабочем положении показаны векторы сил
инерции
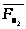 ,
,
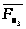 ,
,
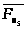 и моменты сил инерции
и моменты сил инерции
 ,
,
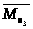 .
Здесь же штриховыми линиями показаны
линейные ускорения центров масс
.
Здесь же штриховыми линиями показаны
линейные ускорения центров масс
 ,
,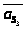 ,
,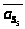 и угловые ускорения
и угловые ускорения
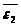 и
и
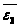 .
.
Определение реакций в кинематических парах и уравновешивающей силы на кривошипе
Определение реакций в кинематических парах следует начинать с той группы Ассура, для которой известны все внешние силы. Такой группой является последняя присоединенная группа Ассура 2 вида, состоящая из звеньев 4, 5.
Рассматриваем
группу 4-5. На данную структурную группу
действуют следующие силы и моменты:
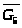 ,
,
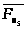 ,
, .
Действие отброшенных звеньев (стойки
0 и кулисы 3) заменяем реакциями
.
Действие отброшенных звеньев (стойки
0 и кулисы 3) заменяем реакциями
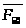 и
и
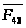 ,
которые необходимо определить.
,
которые необходимо определить.
Величина
и точка приложения реакции в поступательной
паре
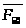 неизвестны, поэтому точка приложения
этой реакции (расстояние
неизвестны, поэтому точка приложения
этой реакции (расстояние
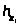 )
выбрано произвольно. Линия действия
реакции
)
выбрано произвольно. Линия действия
реакции
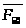 без учета трения перпендикулярна
направляющей этой пары. Реакция во
вращательной паре
без учета трения перпендикулярна
направляющей этой пары. Реакция во
вращательной паре
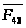 неизвестна по величине и направлению.
Без учета трения эта реакция проходит
через центр шарнира. Разложим реакцию
неизвестна по величине и направлению.
Без учета трения эта реакция проходит
через центр шарнира. Разложим реакцию
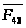 на две составляющие:
на две составляющие:
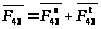
Нормальная
составляющая действует вдоль звена 4:
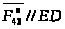 ,
тангенциальная составляющая действует
перпендикулярно звену 4:
,
тангенциальная составляющая действует
перпендикулярно звену 4:
 .
.
Требуется
также определить реакцию во внутренней
вращательной кинематической паре группы
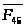 (или
(или
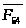 ),
которая без учета трения проходит через
центр шарнира
),
которая без учета трения проходит через
центр шарнира
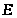 .
Для упорядочения расчетов по определению
реакций составляем таблицу с указанием
очередности определения сил, а также
уравнений, посредством которых они
будут определяться.
.
Для упорядочения расчетов по определению
реакций составляем таблицу с указанием
очередности определения сил, а также
уравнений, посредством которых они
будут определяться.
Таблица
-
№ п/п
Искомая величина
Вид уравнения
Звено, для которого составляется уравнение
1
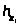
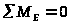
5
2
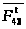
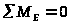
4
3
 ,
,
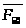

4, 5
4
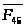 (или
(или
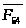 )
)
4 (или 5)
Запишем уравнения, указанные в таблице, в развернутом виде.
Расстояние
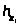 ,
определяющее точку приложения реакции
,
определяющее точку приложения реакции
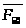 ,
найдем из уравнения моментов для звена
5:
,
найдем из уравнения моментов для звена
5:
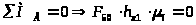 ,
откуда
,
откуда
 .
.
В
данном случае можно было заранее сказать,
что плечо
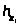 =0,
так как все остальные силы, действующие
на звено 5, проходят через центр шарнира
=0,
так как все остальные силы, действующие
на звено 5, проходят через центр шарнира
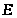 ,
следовательно, и реакция
,
следовательно, и реакция
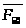 должна проходить через этот центр.
должна проходить через этот центр.
Для
определения реакции
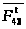 составляем уравнение моментов всех
сил, действующих на звено 4, относительно
точки
составляем уравнение моментов всех
сил, действующих на звено 4, относительно
точки
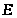 :
:
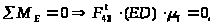 откуда
откуда
 .
.
В
данном случае можно было заранее сказать,
что реакция
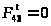 ,
так как все на звено 4 не действует
никаких внешних нагрузок и, следовательно,
реакция должна быть направлена вдоль
звена.
,
так как все на звено 4 не действует
никаких внешних нагрузок и, следовательно,
реакция должна быть направлена вдоль
звена.
Для
определения нормальной составляющей
 и реакции
и реакции
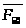 составляем
уравнение статического равновесия
сил, действующих на звенья 4 и 5:
составляем
уравнение статического равновесия
сил, действующих на звенья 4 и 5:
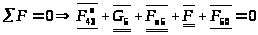
Силы, известные по величине и направлению, подчеркиваем двумя чертами, силы же, известные по направлению – одной чертой.
При составлении векторной суммы сил удобно силы, неизвестные по величине, писать в начале и в конце уравнения, чтобы при построении плана сил было проще пересечь их известные направления. Кроме того, при построении плана сил для всей группы рационально силы, относящиеся к одному звену, наносить последовательно друг за другом, т.е. группировать силы по звеньям, так как это упростит в дальнейшем определение реакции во внутренней кинематической паре.
Отрезки,
изображающие известные силы на плане,
определяем с учетом принятого масштабного
коэффициента
 ,
который выберем по силе резания:
,
который выберем по силе резания:
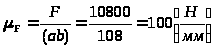 ,
,
где
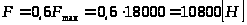 – сила сопротивления,
– сила сопротивления,
 –
отрезок в
–
отрезок в
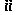 ,
изображающий эту силу на плане сил.
,
изображающий эту силу на плане сил.
Из
произвольной точки в последовательности,
указанной в уравнении, откладываем все
известные векторы, начиная с
 .
Далее через начало вектора
.
Далее через начало вектора
 проводим направление нормальной
составляющей реакции
проводим направление нормальной
составляющей реакции
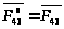 параллельно звену
параллельно звену
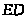 ,
а через конец вектора
,
а через конец вектора
 -
направление реакции
-
направление реакции
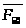 перпендикулярно оси
перпендикулярно оси
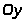 .
Точка пересечения этих направлений
определяет вектора, изображающие в
выбранном масштабе реакции
.
Точка пересечения этих направлений
определяет вектора, изображающие в
выбранном масштабе реакции
 и
и
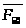 .
Стрелки всех векторов должны соответствовать
одному и тому же направлению обхода
контура плана сил.
.
Стрелки всех векторов должны соответствовать
одному и тому же направлению обхода
контура плана сил.
 ;
;
 .
.
Полная реакция
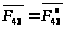 , т.е.
, т.е.
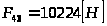 .
.
Для
определения реакции
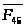 составляем уравнение равновесия сил
для звена 4:
составляем уравнение равновесия сил
для звена 4:
 .
.
Реакция
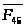 неизвестна ни по величине, ни по
направлению. Очевидно, что она равна по
величине и противоположна по направлению
реакции
неизвестна ни по величине, ни по
направлению. Очевидно, что она равна по
величине и противоположна по направлению
реакции
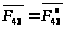 .
Построение показано пунктиром.
.
Построение показано пунктиром.
 .
.
Реакция
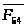 на звено 5 со стороны звена 4 равна по
величине реакции
на звено 5 со стороны звена 4 равна по
величине реакции
 и противоположна ей по направлению.
и противоположна ей по направлению.
Рассмотрев группу Ассура, состоящую из звеньев 4 и 5, переходим к следующей группе – 2ПГ 3 вида, состоящей из звеньев 2 и 3.
Рассматриваем
группу 2-3: На данную структурную группу
действуют следующие силы и моменты:
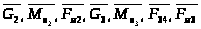 .
Реакция
.
Реакция
 на
звено 3 со стороны звена 4 равна по
величине реакции
на
звено 3 со стороны звена 4 равна по
величине реакции
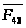 и противоположна ей по направлению
и противоположна ей по направлению
 .
Приложена эта реакция в точке
.
Приложена эта реакция в точке
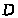 звена 3. Освободив группу 2-3 от связей,
прикладываем вместо них две реакции
звена 3. Освободив группу 2-3 от связей,
прикладываем вместо них две реакции
 в шарнире
в шарнире
 и
и
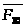 в шарнире
в шарнире
 ,
неизвестные по величине и направлению.
,
неизвестные по величине и направлению.
Разложим
реакцию
 на две составляющие:
на две составляющие:
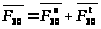
Нормальная
составляющая действует вдоль звена 3:
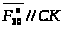 ,
тангенциальная составляющая действует
перпендикулярно звену 3:
,
тангенциальная составляющая действует
перпендикулярно звену 3:
 .
.
Реакцию
 в шарнире
в шарнире
 также разложим на составляющие:
также разложим на составляющие:
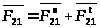 .
.
Нормальная
составляющая действует вдоль звена 2:
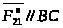 ,
тангенциальная составляющая действует
перпендикулярно звену 2:
,
тангенциальная составляющая действует
перпендикулярно звену 2:
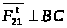 .
.
Требуется
также определить реакцию во внутренней
кинематической паре
 (или
(или
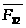 ).
В 2ПГ 1 вида внутренняя кинематическая
пара – вращательная.
).
В 2ПГ 1 вида внутренняя кинематическая
пара – вращательная.
Для упорядочения расчетов по определению реакций составляем таблицу с указанием очередности определения сил, а также уравнений, посредством которых они будут определяться.
Таблица
-
№ п/п
Искомая величина
Вид уравнения
Звено, для которого составляется уравнение
1
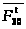

3
2


2
2
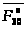 ,
,


3, 2
3
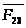 (или
(или
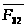 )
)
2 (или 3)
Запишем уравнения, указанные в таблице, в развернутом виде.
Для
определения реакции
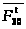 составляем уравнение моментов всех
сил, действующих на звено 2, относительно
точки
составляем уравнение моментов всех
сил, действующих на звено 2, относительно
точки
 :
:
 откуда
откуда

Знак "+" означает, что действительное направление силы соответствует первоначально выбранному.
Для
определения реакции
 составляем уравнение моментов всех
сил, действующих на звено 2, относительно
точки
составляем уравнение моментов всех
сил, действующих на звено 2, относительно
точки
 :
:
 откуда
откуда

Знак "+" означает, что действительное направление силы соответствует первоначально выбранному.
Для
определения нормальной составляющей
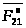 и реакции
и реакции
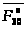 составляем
уравнение статического равновесия
сил, действующих на звенья 3 и 2:
составляем
уравнение статического равновесия
сил, действующих на звенья 3 и 2:
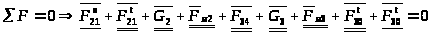
Силы, известные по величине и направлению, подчеркиваем двумя чертами, силы же, известные по направлению – одной чертой.
Отрезки, изображающие известные силы на плане, определяем с учетом ранее принятого масштабного коэффициента
 .
.
Из
произвольной точки в последовательности,
указанной в уравнении, откладываем все
известные векторы, начиная с
 .
Далее через начало вектора
.
Далее через начало вектора
 проводим направление нормальной
составляющей
проводим направление нормальной
составляющей
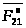 параллельно звену
параллельно звену ,
а через конец вектора
,
а через конец вектора
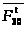 -
направление реакции
-
направление реакции
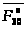 параллельно звену
параллельно звену
 .
Точка пересечения этих направлений
определяет вектора, изображающие в
выбранном масштабе реакции
.
Точка пересечения этих направлений
определяет вектора, изображающие в
выбранном масштабе реакции
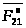 и
и
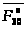 .
Стрелки всех векторов должны соответствовать
одному и тому же направлению обхода
контура плана сил.
.
Стрелки всех векторов должны соответствовать
одному и тому же направлению обхода
контура плана сил.
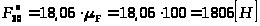 ;
;
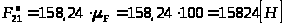 .
.
Полную
реакцию
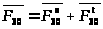 получим, соединив начало вектора
получим, соединив начало вектора
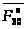 с концом вектора
с концом вектора
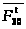 ,
а значение можно определить, пользуясь
формулой:
,
а значение можно определить, пользуясь
формулой:
 .
.
Полную
реакцию
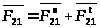 получим, соединив начало вектора
получим, соединив начало вектора
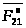 с концом вектора
с концом вектора
 ,
а значение можно определить, пользуясь
формулой:
,
а значение можно определить, пользуясь
формулой:
 .
.
Для
определения реакции
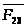 составляем уравнение равновесия сил
для звена 2:
составляем уравнение равновесия сил
для звена 2:
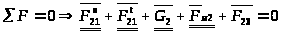 .
.
Реакция
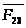 неизвестна ни по величине, ни по
направлению. Новый план сил для звена
2 можно не строить, так как при построении
плана сил для группы 2-3 силы были
сгруппированы по звеньям. Для определения
реакции
неизвестна ни по величине, ни по
направлению. Новый план сил для звена
2 можно не строить, так как при построении
плана сил для группы 2-3 силы были
сгруппированы по звеньям. Для определения
реакции
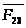 достаточно соединить конец вектора
достаточно соединить конец вектора
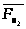 c
началом вектора
c
началом вектора
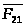
 (построение
показано штриховой линией).
(построение
показано штриховой линией).
 .
.
Реакция
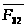 на звено 3 со стороны звена 2 равна по
величине реакции
на звено 3 со стороны звена 2 равна по
величине реакции
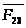 и противоположна ей по направлению.
и противоположна ей по направлению.
Определив реакции во всех кинематических парах 2ПГ 1 вида, состоящей из звеньев 2 и 3, переходим к рассмотрению начального звена 1.
Рассматриваем
начальное звено 1: на кривошип действует
известная по величине и направлению
реакция
 (по условию задачи массу звена 1 не
учитываем). Определим реакцию
(по условию задачи массу звена 1 не
учитываем). Определим реакцию
 cо
стороны отброшенной стойки 0 и
уравновешивающую силу
cо
стороны отброшенной стойки 0 и
уравновешивающую силу
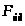 .
Величина уравновешивающей силы может
быть определена при условии, что известны
линия ее действия и точка приложения.
При выполнении курсового проекта условно
принимают, что линия действия
уравновешивающей силы проходит через
точку
.
Величина уравновешивающей силы может
быть определена при условии, что известны
линия ее действия и точка приложения.
При выполнении курсового проекта условно
принимают, что линия действия
уравновешивающей силы проходит через
точку
 перпендикулярно
перпендикулярно
 .
.
Для упорядочения расчетов по определению реакций составляем таблицу с указанием очередности определения сил, а также уравнений, посредством которых они будут определяться.
Таблица
-
№ п/п
Искомая величина
Вид уравнения
Звено, для которого составляется уравнение
1


1
2
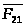

1
Запишем уравнения, указанные в таблице, в развернутом виде.
Для
определения
 составляем уравнение моментов всех
сил, действующих на кривошип, относительно
точки
составляем уравнение моментов всех
сил, действующих на кривошип, относительно
точки
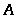 :
:
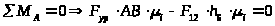 ,
откуда
,
откуда
 .
.
Для
определения реакции со стороны
отброшенной стойки
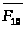 составляем уравнение статического
равновесия сил, действующих на звено
1:
составляем уравнение статического
равновесия сил, действующих на звено
1:

Уравновешивающая
сила и реакция
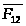 известны по величине и направлению, а
замыкающий вектор – искомая реакция
известны по величине и направлению, а
замыкающий вектор – искомая реакция
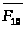 .
.
Отрезки, изображающие известные силы на плане, определяем с учетом ранее принятого масштабного коэффициента
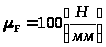 .
.
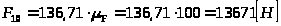
Определение уравновешивающей силы с помощью рычага Жуковского
В качестве проверки определим для рассматриваемого положения механизма уравновешивающую силу с помощью рычага Жуковского.
Решение задачи ведем в следующей последовательности.
План скоростей для рассматриваемого рабочего положения механизма поворачиваем на 900 в сторону, противоположную вращению кривошипа.
Все
силы, действующие на звенья механизма,
включая силы инерции и искомую
уравновешивающую силу, переносим
параллельно самим себе в одноименные
точки повернутого плана. Если на звено
действует момент сил, то этот момент
следует предварительно представить на
звене механизма как пару сил, вычислив
их величины. Плечо пары выбирается на
звене, к которому приложен момент,
произвольно. В условиях данного курсового
нужно перенести на рычаг Жуковского
моменты сил инерции:
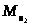 ,
,
 .
.
Представим
момент
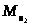 на шатуне 2 в виде пары сил
на шатуне 2 в виде пары сил
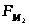 ,
приложенных в точках
,
приложенных в точках
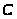 и
и
 перпендикулярно выбранному плечу
перпендикулярно выбранному плечу
 так, чтобы направление действия момента
на звено было сохранено. Тогда
так, чтобы направление действия момента
на звено было сохранено. Тогда
 .
.
Момент
 на звене 3 представим в виде пары сил
на звене 3 представим в виде пары сил
 ,
приложенных в точках
,
приложенных в точках
 и
и
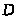 этого звена перпендикулярно звену
этого звена перпендикулярно звену
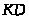 :
:
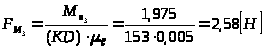 .
.
Найденные силы пар переносим на рычаг Жуковского по общему правилу.
Составляем уравнение моментов всех сил относительно полюса повернутого плана скоростей:

откуда
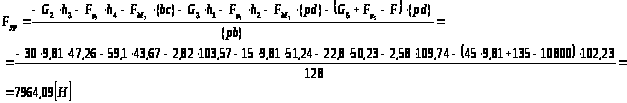
Полученную с помощью рычага Жуковского уравновешивающую силу нужно сравнить с силой, полученной в результате кинетостатического расчета. При выполнении курсового проекта относительная разность не должна превышать 5%.
Выполним проверку:
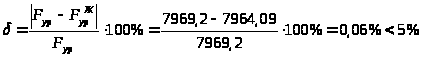 .
– верно.
.
– верно.
Следовательно, расчет уравновешивающей нагрузки выполнен правильно.