Квантовые свойства излучения

РЕФЕРАТ

Квантовые свойства излучения.

В конце XIX века волновая теория природы света, как казалось, окончательно победила ньютоновскую корпускулярную теорию. Электромагнитная природа света точно описывала природу этих световых волн – это электрическое, а, следовательно, и магнитное поле, изменяющееся периодически во времени и распространяющееся в пространстве. Это прекрасно подтверждалось явлениями дифракции и поляризационной интерференции света.

Первое явление, которое не могло быть объяснено на основе волновой теории света – это излучение черного тела и экспериментальные законы теплового излучения. Для разрешения этой проблемы М. Планк сформулировал первую квантово-механическую гипотезу и сначала эмпирически (на основе рассуждений и предположений), а потом и теоретически вывел свою знаменитую формулу (1900 г): E = hν илиE = ħω, где h – постоянная Планка ().

Ну, а теперь остановимся подробнее на явлении теплового излучения, его основных характеристиках и законах.

Тепловое излучение.

Излучение (или испускание) электромагнитных волн веществом происходит из-за внутриатомных (внутримолекулярных) процессов.

Источники энергий, которые могут вызывать излучение и виды возникающего излучения:

- энергия химических реакций (хемилюминесценция);

- энергия газового разряда (электролюминесценция);

- энергия бомбардирующих твердое тело электронов (катодолюминесценция).

Но существует один вид излучения, присущий всем физическим телам.

Тепловое излучение – это электромагнитное излучение, возникающее за счет внутренней (тепловой) энергии излучающего тела и зависящее только от температуры и оптических свойств данного физического тела.

Тепловое излучение возникает при любых температурах (естественно, больших, чем Т=0К), следовательно, испускается всеми телами. В зависимости от температуры тела изменяется интенсивность и спектральный состав излучения. При высокой температуре возникает свечение белого цвета (сплошной спектр). При понижении температуры Т возрастает длина волны излучения λ, т.е. цвет свечения изменяется от желтого к красному и инфракрасному вплоть до полного прекращения видимого свечения: тело испускает только невидимые глазом ИК лучи.

Тепловое излучение – единственный вид излучения, который находится в термодинамическом равновесии с излучающим телом, т.е. является равновесным (тело в единицу времени поглощает столько же энергии, сколько и излучает). Равновесное излучение устанавливается в теплоизолированной (адиабатно замкнутой) системе.

Пример. Излучающее тело в оболочке с идеально отражающей поверхностью.

Излучение испускается телом, отражается оболочкой, затем вновь поглощается и отражается телом и т.д. Энергия, излучаемая телом, компенсируется за счет поглощения им такого же количества энергии падающего на него излучения.

Свойство теплового излучения находиться в термодинамическом равновесии с излучающим телом обусловлено тем, что интенсивность теплового излучения возрастает с увеличением температуры.

Пусть выполняется соотношение энергий, когда Еизл > Eпогл, следовательно, температура тела и его внутренняя энергия будут уменьшаться. Это, в свою очередь, приводит к уменьшению интенсивности теплового излучения до тех пор, пока Еизл не станет равной Eпогл (Еизл = Eпогл) и наоборот.

Таким образом, равновесие системы "тепловое излучение – тело" является устойчивым (т.е. при отклонении в какую либо сторону возникают процессы, возвращающие систему в термодинамическое равновесие).

Характеристики теплового излучения.

Интегральные характеристики.

1. Поток излучения Ф – это средняя мощность излучения за время, значительно большее периода электромагнитных (световых) колебаний, размерность Ф – [Вт].

2. Энергетическая светимость Rλ,T, Rω,T – это поток излучения (энергии), испускаемый единицей поверхности (1 м2) по всем направлениям (т.е. в пределах телесного угла 2π), является функцией температуры Т и длины волны λ или частоты ω излучения. Размерность – [Вт/м2].

Тело излучает электромагнитные волны различных частот ω (или длин волн λ). Выделим интервал частот от ω до ω+dω. Энергия и, следовательно, мощность (поток) излучения в интервале dω будут пропорциональны величине самого интервала dω:

dRω= rω dωиdRλ = rλ dλ, причем очевидно, чтоdRω = dRλ.

Тогда полный поток энергии

(интегрирование проводится по всему спектру излучения).

Здесь rω и rλ – дифференциальные характеристики излучения, которые называются спектральная плотность энергетической светимости тела или мощность излучения с единицы поверхности тела в единичном интервале частот. Эти характеристики определяют испускательную способность тела.

Определим связь между rω и rλ. Так какdRω = dRλ, т.е. rωdω = rλdλ, и с учетом того, что

λ = =, т.е. dλ= – dω = – dω

(знак "–" означает, что с увеличением λ величина ω уменьшается и наоборот), имеем:

rω dω = rλ dλ =

rλ dω,

следовательно:

rω = rλ = rλ.

С помощью аналогичных рассуждений можно получить соотношение между rν и rλ:

rν = 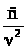rλ = rλ.

3. Способность тела поглощать излучение характеризуется коэффициентом поглощения:

α = ,

т.е. отношением величин потоков поглощенного и падающего на тело излучений. Коэффициент α – величина безразмерная; ее значение находится в диапазоне {0 < α < 1}.

Если выделить излучение в интервале частот dω (или длин волн dλ), то отношение элементарных потоков энергии dФ (поглощенного к падающему ) будет зависеть от величины диапазона частот (или длин волн):

аω= (в интервале dω), аλ= (в интервале dλ)

Таким образом, вводится еще одна дифференциальная характеристика аω (или аλ) – поглощательная способность тела (или монохроматический коэффициент поглощения).

Дифференциальные характеристики rω и аω зависят от частоты или длины волны излучаемого (поглощаемого) излучения, температуры и химического состава тела, а также от состояния его поверхности.

Очевидно, что величина аω также, как и коэффициент поглощения α меняется в интервале от нуля до единицы. Сильнее других поглощают излучение тела черного цвета (примеры…).

Абсолютно черное тело – это тело, которое при любой температуре полностью поглощает всю энергию падающих электромагнитных волн независимо от их частоты, поляризации и направления распространения, т.е. коэффициенты поглощения α0≡ ≡ 1. Испускательная способность черного тела обозначается – .

Абсолютно черного тела в природе не существует; наиболее совершенной его моделью является замкнутая полость с небольшим отверстием, непрозрачными и отражающими стенками, обеспечивающими многократное отражение луча. При каждом отражении луч частично поглощается. Независимо от материала стенок интенсивность выходящего потока будет намного меньше интенсивности входящего первоначального излучения.

В теории теплового излучения часто пользуются идеализированной моделью реальных тел – понятием "серое тело". Тело называется "серым", если его коэффициент поглощения одинаков для всех частот и зависит только от температуры материала и состояния его поверхности аωс = аωс(Т).

В действительности реальное физическое тело по своим характеристикам приближается к серому телу только в узком диапазоне частот излучения.

Связь между испускательной и поглощательной способностями тела.

Пусть в замкнутой адиабатичной (теплоизолированной) оболочке находятся несколько тел (включая абсолютно черное тело) в состоянии термодинамического равновесия. Пусть температуры всех тел одинаковы, но даже, если бы они были различны, то через некоторое время выровнялись бы. Состояние тел в такой системе не может измениться. Следовательно, тело, обладающее большей испускательной способностью для данной частоты (длины волны) излучения, должно интенсивнее поглощать излучение этой же частоты, иначе его энергия (температура) изменилась бы (при увеличении энергии излучения тела его температура уменьшается). И наоборот. То есть должно выполняться соотношение:

Здесь – испускательная способность черного тела, при этом поглощательная способность черного тела = 1.

Закон теплового излучения Кирхгофа (1859г)

Отношение спектральной плотности энергетической светимости тела к его монохроматическому коэффициенту поглощения не зависит от материала тела (т. е одинаково для всех тел) и равно спектральной плотности энергетической светимости абсолютно черного тела. Данная величина является функцией только температуры и частоты излучения.

Более простая формулировка закона: при одинаковой температуре отношение 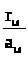одинаково для всех, в том числе и для черных, тел.

Дифференциальная форма закона Кирхгофа:

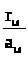= (Т, ω) или = aω·.

Следствия закона Кирхгофа.

I. Так как коэффициент поглощения aω для любого тела меньше единицы (aω < 1), то испускательная способность любого тела для данной частоты излучения меньше таковой для черного тела: < .

Иначе говоря, черное тело при любой температуре и частоте излучения является наиболее интенсивным источником излучения.

II. Если тело не поглощает излучения в какой-либо области спектра (aω = 0), то оно и не излучает в этой области спектра, т.е. rω = 0 (при данной температуре).

III. Зная спектр излучения черного тела при данной температуре () и зависимость монохроматического коэффициента поглощения данного тела от частоты (aω(ω)), можно найти спектр излучения тела rω(ω).

Интегральная форма закона Кирхгофа записывается для энергетической светимости во всем диапазоне частот:

Так как

, а для серых тел

и может быть вынесена за знак интеграла, то

где – энергетическая светимость черного тела.

Для данной температуры сильнее излучают те серые тела, которые обладают большим коэффициентом поглощения.

Законы теплового излучения черного тела (Стефана – Больцмана и Вина)

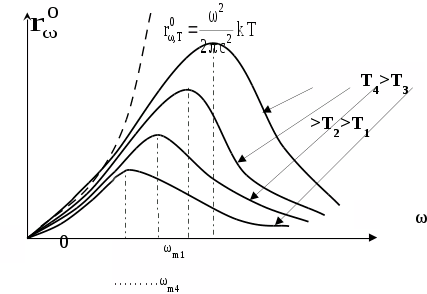
Экспериментально было установлено, что тепловое излучение черного тела имеет сплошной спектр. Схематические графики спектров для различных температур представлены на рисунке.

Из приведенных рисунков следует:

Т

ак как r_>ω> и r_>λ>. не пропорциональны друг другу, а связаны соотношением r_>ω>_>
=> r_>λ>, и их максимумы находятся в разных частях спектра, то:

для каждой температуры существует максимум испускательной способности , который с увеличением температуры смещается в область бо'льших частот излучения (т.е. в область меньших длин волн);

т. к. энергетическая светимость черного тела равна площади под графиком rω0 (ω), то R0 увеличивается с повышением температуры (т.е. энергетическая светимость возрастает по мере нагревания черного тела).

Очень важная для характеристики теплового излучения величина – спектральная плотность энергетической светимости черного тела (испускательная способность), долгое время не могла быть вычислена теоретически, т. к. рассматривалась как классическая величина.

Рэлей и Джинс (1900 г) попытались обосновать экспериментальные зависимости с помощью классической статистической физики. Рэлей подошел к изучению спектральных закономерностей излучения черного тела с позиций статистической физики, а не термодинамики, как это делалось ранее. Он рассматривал равновесное излучение черного тела в замкнутой полости с отражающими стенками как совокупность пространственных электромагнитных стоячих волн. При этом колебания с различными частотами совершаются независимо друг от друга, и каждой частоте соответствует своя колебательная степень свободы. Рэлей применил к тепловому излучению закон классической статистической физики равномерного распределения энергии по степеням свободы, согласно которому на каждую степень свободы приходится энергия, равная kT. В частности, он предположил, что на каждое электромагнитное колебание в среднем приходится энергия, равная двум половинкам kT (одна – на электрическую, другая – на магнитную составляющую энергии волны). Таким образом, Рэлей и Джинс, считая среднюю энергию излучающего атомного осциллятора равной kТ, вывели формулу для спектральной плотности светимости черного тела:

(1)

Однако эта формула согласуется с экспериментами только в области малых частот и при высоких температурах. Для больших частот она явно неверна. Энергетическая светимость черного тела с учетом формулы Рэлея – Джинса

Невозможность обоснования законов излучения черного тела с помощью классической теоретической физики получило название "ультрафиолетовой катастрофы" (УФ – диапазону соответствуют малые длины волн λ и высокие частоты ω).

Теоретическое определение было получено М. Планком (1900 г), который отказался от установившегося положения классической физики о том, что энергия физической системы меняется непрерывно. Планк ввел понятие квантования излучения (поглощения) и сформулировал знаменитую гипотезу Планка: тела излучают (и поглощают) энергию не непрерывно, а дискретными порциями (квантами)

E = hν = ħωω = 2πν

h = 6,62·10-34 Дж·с – постоянная Планка; ħ = 1,054·10-34 Дж·с.

Представляя излучающее тело как совокупность гармонических атомов – осцилляторов, каждый их которых излучает квант энергии hν (ħω), Планк получил выражение для средней энергии осциллятора: 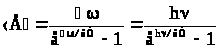, подставив которое в формулу Рэлея – Джинса, получим

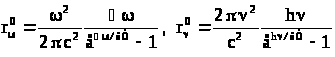Выражения для и , которые называют формулой Планка, блестяще согласуются с экспериментальными зависимостями. Используя соотношение между rν и rλ и формулу Рэлея – Джинса, получим формулу Планка для .

Так как

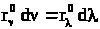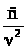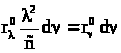dRν = dRλ,, аλ = , т.е. dλ= – dν = – dν, то: и.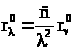

Подставляя формулу Рэлея – Джинса для , получаем:

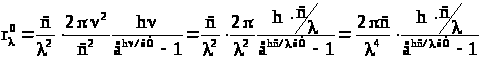, или окончательно

Формула Планка переходит в формулу Рэлея – Джинса (1) при hν = ħω << kT, когда энергия излучаемого кванта много меньше энергии теплового движения. Действительно,

Теперь вычислим энергетическую светимость R0:

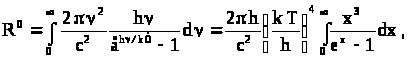
где введена безразмерная переменная

Интеграл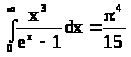, тогда

где σ – постоянная Стефана – Больцмана: σ = 5,7·10-8 Вт/м2К4.

Таким образом, мы получили закон Стефана – Больцмана для энергетической светимости черного тела, который гласит: энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры.

Стефан получил эту зависимость на основе экспериментов (1879 г), а Больцман, применив методы классической термодинамики, вывел ее теоретически (1884 г). Согласно этому закону энергетическая светимость черного тела является определенной величиной, и не равна бесконечности, как в случае использования формулы Рэлея – Джинса.

Так как энергетическая светимость серых тел RC = aC·R0 для серых тел закон Стефана – Больцмана приобретает вид: RC = aC·σ·Т4, где аС – коэффициент поглощения, не зависящий от λ (или ω), но зависящий от температуры.

Вернемся к экспериментальным графикам спектральных плотностей энергетической светимости черного тела и . Из них следует еще один закон теплового излучения черного тела. Используя формулу Планка для величин и , из условий:

можно определить значения ωm и λm, соответствующие максимумам

и . Действительно, так как,

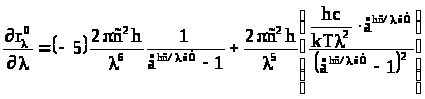
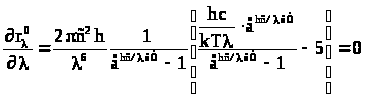Введем переменную , тогда условие максимума будет иметь вид: .

Это трансцендентное уравнение решается методом последовательных приближений и дает значение х = 4,965, откуда

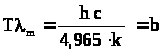Соотношения λm = b/T иνm/T = ωm/2πT = b1 (b = 2,9·10-3 м·К – постоянная Вина) выражают закон смещения Вина (1893 г):

длина волны, соответствующая максимальной спектральной плотности энергетической светимости черного тела, обратно пропорциональна его термодинамической температуре.

Или: частота, соответствующая максимальной спектральной плотности энергетической светимости черного тела, прямо пропорциональна его термодинамической температуре.

Из закона Вина непосредственно следует, что при понижении температуры тела максимум энергии его излучения смещается в область бо'льших длин волн. Становится понятным, почему при уменьшении температуры светящихся тел белое свечение становится желтым, затем – красным, а после этого вообще становится невидимым. Это происходит из-за того, что в спектре начинает преобладать длинноволновое излучение.

Таким образом, первая квантово-механическая гипотеза Планка о квантованности излучения (поглощения) и последующий вывод формулы для спектральной плотности энергетической светимости черного тела позволили получить теоретическое обоснование экспериментально наблюдавшихся законов излучения черного тела.