Проектирование крытого рынка
Пермский Государственный Технический Университет
Кафедра Строительных Конструкций
КУРСОВОЙ ПРОЕКТ
По дисциплине «Конструкции из дерева и пластмасс»
на тему «Проектирование крытого рынка»
Выполнил:
Ашихмин А.Г.
Проверил:
Фаизов И.Н.
Пермь 2009
1. Расчет щита покрытия
1.1 Исходные данные
Условия эксплуатации нормальные.
Уклон кровли 1:4.
Материал обшивок панелей деревянные щиты из ели 2-го сорта.
Каркас плиты из древесины ели 2-го сорта.
Шаг несущих конструкций – 4,5 м.
Шаг прогонов – 1 м.
1.2 Расчёт конструкции покрытия
Настил рассчитываем как многопролетную неразрезную балку. Расчет ведется для полосы настила, шириной 1 метр с учетом числа досок рабочего слоя на этой ширине. При расчете настила учитываем:
- постоянная нагрузка от покрытия равномерно распределена по поверхности кровли;
- снеговая нагрузка распределяется на горизонтальную проекцию кровли;
- ветровая нагрузка при углах наклона кровли до 30о, разгружает Настилы и в расчетах не учитывается;
- временная нагрузка от сосредоточенного груза равна 1,2 кН и распределена на ширину 0,5 м настила (P=2,4 кН)
Расчёт деревянного щита покрытия ведем на два сочетания нагрузок:
I сочетание: постоянная + временная снеговая
(q/>p>=q/>пост>+s/)
II сочетание: постоянная + временная от сосредоточенного груза
(q/>p>=q/>пост>+Р/)
А. постоянные нагрузки
- где
Б. временные нагрузки
Снеговая нагрузка
нормативное
значение веса снегового покрова (V
снеговой район)
при
уклоне кровли не более 25о
1.3 Сбор нагрузок
|
Наименование нагрузки |
Нормативная Н/м2 |
коэффициент надежности |
Расчетная Н/м2 |
|
А. Постоянные |
|||
|
Собственная масса щита покрытия |
0,3 |
1,1 |
0,33 |
|
Б. Временные |
|||
|
Снеговая |
2,24 |
1/0,7 |
3,2 |
|
ВСЕГО: |
2,54 |
3,52 |
Расчетные погонные нагрузки:
- от собств. массы щита покрытия:
- от снеговой нагрузки
- от временной сосредоточенной
1.4 Статический расчет щита
Плита рассчитывается по схеме многопролетной балки. Пролет l>р> равен шагу прогонов – 1 м.
Расчетные сочетания нагрузок:
I сочетание (постоянная + временная снеговая)
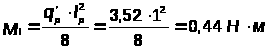
II сочетание (постоянная + временная от сосредоточенного груза)
1.5 Конструктивный расчет щита
Расчет характеристики материала:
где:
- расч. сопротивление древесины
на изгиб (ель 2-го сорта)
1,15 – коэф., учитывающий менее ответственную работу настилов
0,85 – коэф. условия эксплуатации
Требуемый момент сопротивления поперечного сечения щита покрытия должен быть не менее:
Требуемая общая ширина досок на расчетной ширине 1м равна:
Фактический момент сопротивления при расчетной ширине 1м равен:
Нормативные напряжения:
Относительный прогиб проверяем при первом сочетании нагрузок:
Вывод:
Подобранное сечение удовлетворяет условиям прочности и жесткости.
2. Расчет прогонов
2.1 Сбор нагрузок на 1 м2 покрытия
|
Наименование нагрузки |
Нормативная Н/м2 |
коэффициент надежности |
Расчетная Н/м2 |
|
А. Постоянные |
|||
|
Собственная масса щита покрытия |
0,3 |
1,1 |
0,33 |
|
Собств. вес прогона(ориентировочно) |
0,1 |
1,1 |
0,11 |
|
Б. Временные |
|||
|
Снеговая |
2,24 |
1/0,7 |
3,2 |
|
ВСЕГО: |
2,8 |
3,63 |
2.2 Статический расчет прогона
Расчетная погонная
нагрузка на прогон:
;
Расчетную схему прогона примем разрезную, тогда
Расчетный пролет прогона:
см,
где b – шаг несущих конструкций, а=10 см – ширина опорной площадки прогона.
Максимальный изгибающий момент в прогоне:
.
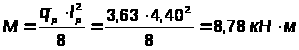Прогон работает в условиях косого изгиба. Составляющие момента относительно главных осей сечения:
,
,
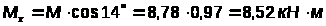2.3 Конструктивный расчет прогона
Минимальные размеры поперечного
сечения прогона получаются из условия
обеспечения требуемой жесткости при
.
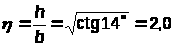Требуемый момент сопротивления сечения
см3.
Где
– расчетное сопротивление древесины
изгибу.
Требуемая высота сечения:
cм.
Требуемая ширина сечения:
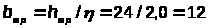cм.
По сортаменту пиломатериалов принимаем брус сечением 125х250, с геометрическими характеристиками:
,
,
,
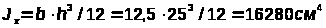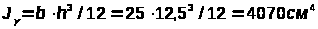Проверку прочности не выполняем, так как при подборе сечения мы исходили из главной формулы.
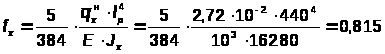см,
где
кН/м.
см,
где
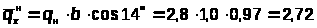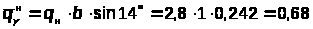кН/м.
Полный прогиб прогона определяется по формуле
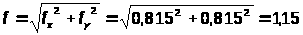см
<
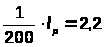cм.
Жесткость прогона обеспечена.
3. Расчет рамы
Рамы из прямолинейных элементов с соединением ригеля и стойки на зубчатый шип являются наиболее технологичными и простыми в изготовлении. Для их изготовления склеивается прямолинейная заготовка, которая затем распиливается по диагонали на два ригеля и две стойки. Для образования карнизного узла по длине биссектрисного сечения фрезеруется зубчатый шип и производится склеивание в специальном приспособлении, обеспечивающем необходимое давление запрессовки и требуемую геометрию узла.
Существенным недостатком этих рам является наличие ослабления в наиболее напряженном сечении. Надежность и долговечность всей конструкции зависит от качества клеевого соединения, которое достаточно сложно проконтролировать.
3.1 Геометрический расчет
На стадии подготовки исходных данных на проектирование задаемся основными геометрическими размерами рамы
пролет 1=15 м,
высота стойки Н=4 м,
уклон ригеля i=0,25.
В зависимости от этих параметров вычисляем длину стоек, ригеля по геометрическим осям.
3.2 Сбор нагрузок
Таблица 2 - Нагрузки на раму (Н/м2)
|
Наименование нагрузок |
Нормативные нагрузки |
>f> |
Расчетные нагрузки |
|
А: Постоянные Масса щита покрытия Вес прогона Собственный вес рамы |
0,3 0,19 |
1,1 1,1 |
0,33 0,21 |
|
Итого: |
0,49 |
0,54 |
|
|
Б: Временные - Снеговая |
2,24 |
1/0,7 |
3,2 |
|
Полная нагрузка: |
2,73 |
3,74 |
Собственная масса рамы:
gн>с.м.>
=
Н/м2;
где gн>п> – нормативная нагрузка от собственной массы покрытия;
gн>сн> – нормативная снеговая нагрузка на покрытие;
к>см> – коэффициент собственной массы несущих конструкций.
Полные погонные нагрузки:
а) постоянная g>п> = 0,54 · 4,5 = 2,43 кН/м;
б) временная g>сн> = 3,2· 4,5 = 14,4 кН/м;
в) полная g = g>п> + g>сн> = 16,83 кН/м
3.3 Ветровая нагрузка
Ветровая нагрузка принимается по табл. 5 и приложению 3 СНиПа [1].
Город Чусовой находится во II ветровом районе, нормативное ветровое давление на покрытие W>o>= 0,3 МПа.
Расчетное значение ветровой нагрузки определяется по формуле
W= W>o>∙k∙c γ>f>;
где k – коэффициент, учитывающий изменение ветрового давления по высоте;
c – аэродинамический коэффициент, учитывающий форму покрытия
γ>f> = 1,4 – коэффициент надежности по нагрузке;
Погонные расчетные значения ветровой нагрузки
W>1>= W>1>∙ B= 0,3∙ 0,5∙ 0,8∙ 1,4∙ 4,5= 0,756 кН/м;
W>2>= W>2>∙ B= 0,3∙ 0,5∙ (-0,2)∙ 1,4∙ 4,5= -0,189 кН/м;
W>3>= W>3>∙ B= 0,3∙ 0,5∙ (-0,4)∙ 1,4∙ 4,5= -0,378 кН/м;
W>4>= W>4>∙ B= 0,3∙ 0,5∙ (-0,5)∙ 1,4∙ 4,5= -0,473 кН/м;
3.4 Расчет сочетаний нагрузок
Расчет сочетаний нагрузок производим по правилам строительной механики на ЭВМ с использованием расчетного комплекса «Лира Windows 9.0». Сочетание нагрузок.
Расчетные сочетания нагрузок принимаются в соответствии с п.п. 1.10.-1.13.СНиП [1]. Расчет ведется на одно или несколько основных сочетаний нагрузок.
Первое сочетание нагрузок включает в себя постоянную и снеговую нагрузки по всему пролету:
qI= g + S, кН/м
Второе сочетание нагрузок включает в себя постоянную и снеговую нагрузки по всему пролету совместно с ветровой нагрузкой (рис. 1, 2, 3):
qII= g + 0,9∙(S + W), кН/м
Рис. 1 - Эпюра изгибающих моментов по 2 РСН
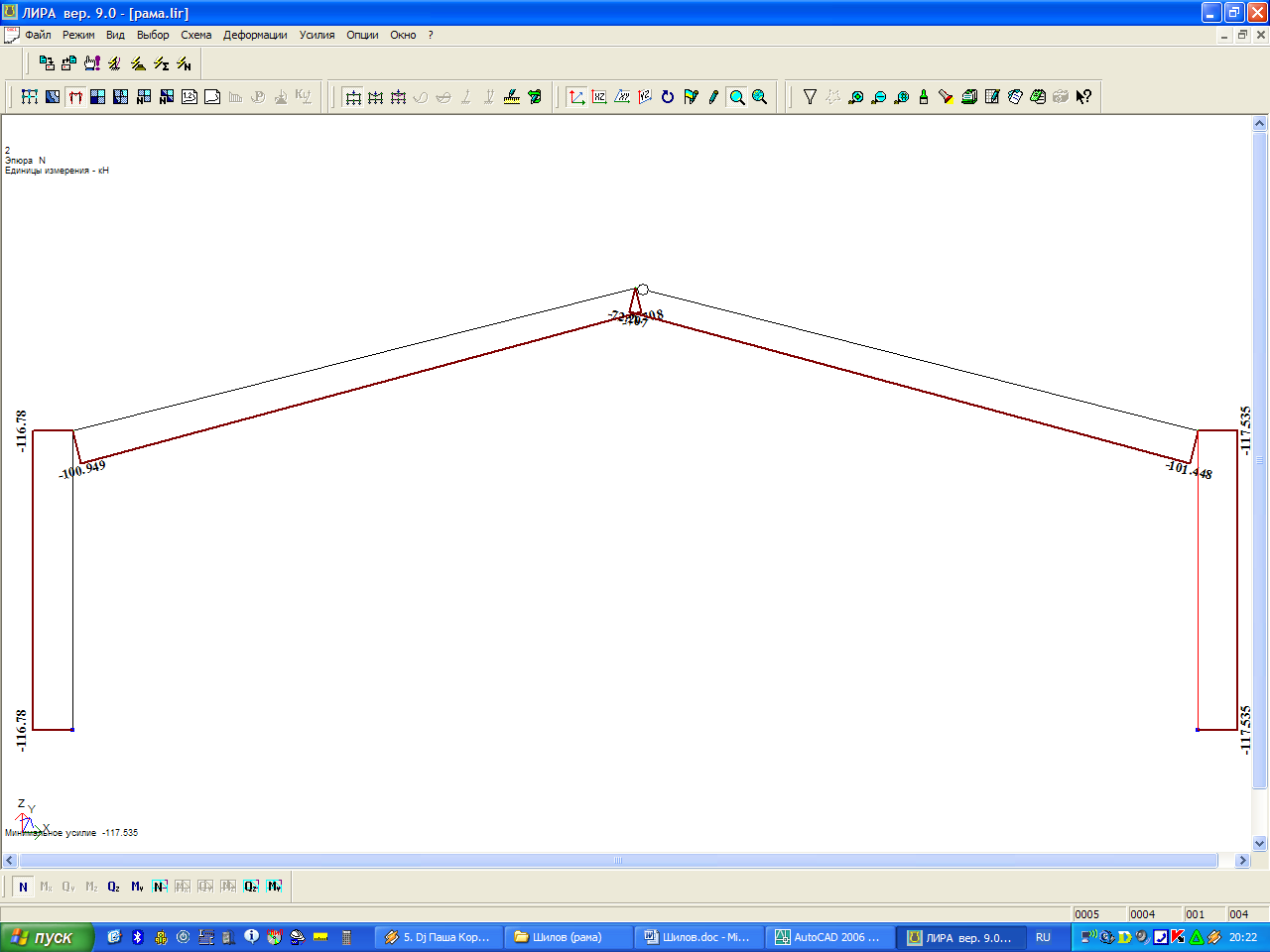
Рис. 2 - Эпюра продольных сил по 2 РСН
Рис. 3 - Эпюра поперечных сил по 2 РСН
Третье сочетание нагрузок включает в себя постоянную нагрузку по всему пролету, снеговую нагрузку на половине пролета и ветровую нагрузку (рис. 4, 5, 6):
qIII= g + 0,9∙(S’ + W), кН/м
Рис. 4 - Эпюра изгибающих моментов по 3 РСН
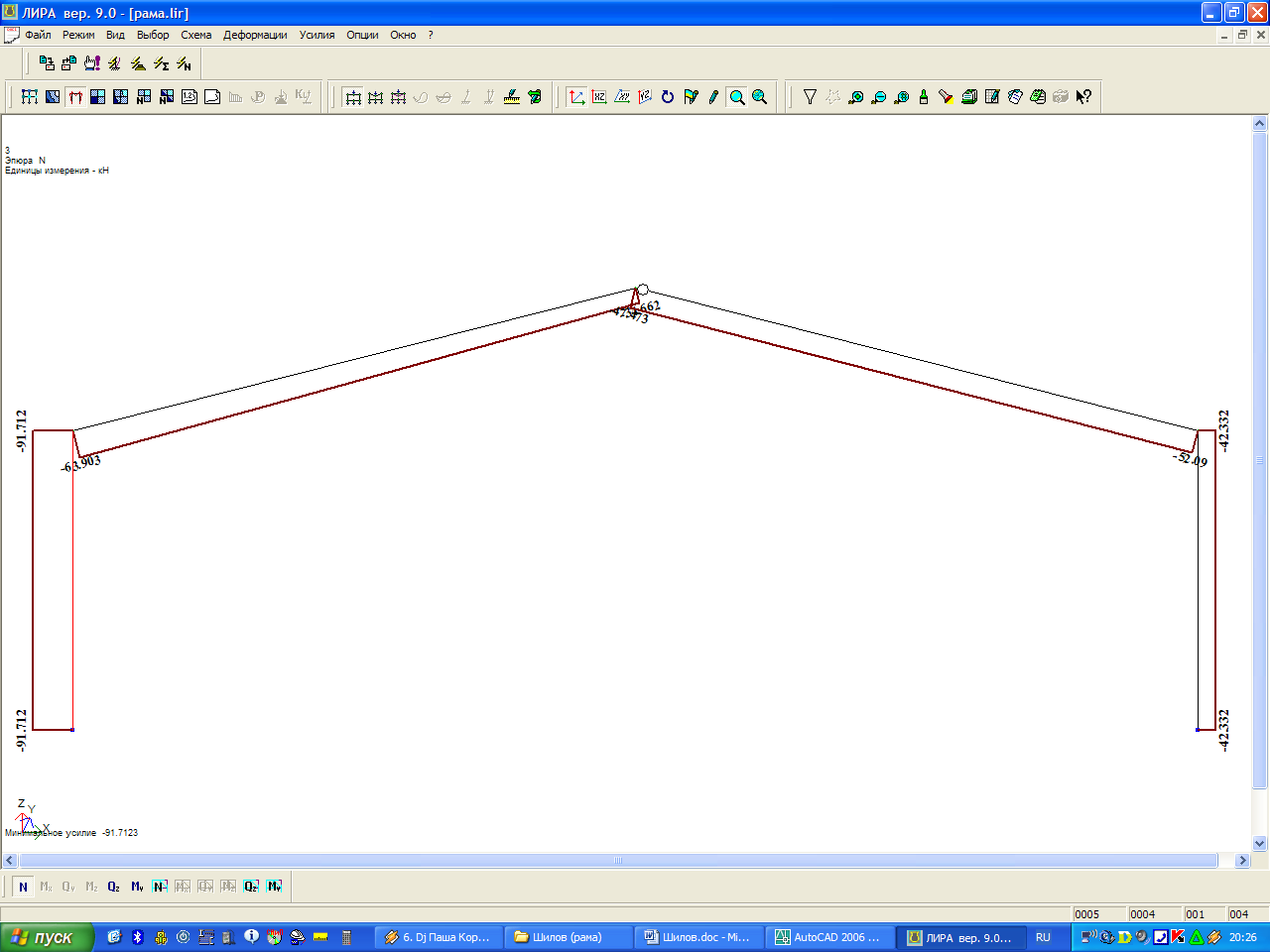
Рис. 5 - Эпюра продольных сил по 3 РСН
Рис. 6 - Эпюра поперечных сил по 3 РСН
Наибольшие усилия в элементах арки (карнизный узел):
продольная сила N= - 130 кН;
поперечная сила Q= - 106 кН;
изгибающий момент М= + 331 кНм.
Коньковый узел
продольная сила N= - 82 кН;
поперечная сила Q= - 21 кН.
Опорный узел
продольная сила N= - 130 кН;
поперечная сила Q= + 83 кН.
3.5 Конструктивный расчет рамы
Конструктивный расчет преследует цель определить сечения элементов рамы и конструкцию узлов.
Несущий каркас здания представлен в виде однопролетных симметричных сборных рам с двускатным ригелем. Рамы решены по трехшарнирной схеме с шарнирными опорными и коньковым узлам и жесткими карнизными узлами. Жесткость последних обеспечивается сопряжением ригеля со стойкой на зубчатый шип.
Стойки рам опираются на столбчатые бетонные фундаменты, возвышающиеся над уровнем пола на 20 см. Полная высота стойки h>ст> = 3,8 м. Уклон кровли i =1:4.
3.6 Подбор сечения полуарки
Раму проектируем клееной из досок толщиной с учетом острожки 32 мм.
Коэффициент надежности по назначению γ>n> = 0,95.
Сечение рамы принимается клееным прямоугольным. Ширина сечения b = 140 мм;
Материал – ель первого сорта.
Принимем размеры поперечного сечения рамы исходя из условий
h = l /20 – l /40 = (15/20…15/40) = (0,38…0,75)м;
h>оп> = 0,3 h;
h>к>= 0,4 h.
h = 500 мм, h>оп> = 150 мм, h>к >= 200 мм.
3.7 Проверка прочности биссектрисного сечения
Проверка прочности биссектрисного сечения производится с учетом технологического ослабления сечения зубчатым шипом и криволинейностью эпюры напряжения по формулам:
- внутренняя сжатая зона
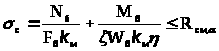
- растянутая наружная кромка
где
=-130
кН – расчетная продольная сила в
карнизном узле;
где
=331
кНм – расчетный изгибающий момент в
карнизном узле;
k>м>=0,85 – коэффициент технологического ослабления сечения;
-
коэффициент, учитывающий криволинейность
эпюры напряжений в биссектрисном
сечении;
h>>> >= h/соs39о=50/0,777=64,3 см- высота биссектрисного сечения;
F>> = bh>> =14∙64,3=900,2 см2- площадь биссектрисного сечения;
W>> =(bh>>2)/6 = 14∙64,32/6= 9647 см3-расчетный момент сопротивления;
k=0,5 – безразмерный коэффициент, при уклоне ригеля рамы i=1/4;
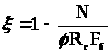
коэффициент, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента, определяемый по формуле;
l>о> = l>0>=(7,7+4)∙1=11,7 м -расчетная длина элемента;
–
радиус инерции сечения;
- гибкость элемента цельного
сечения;
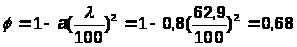- коэффициент продольного изгиба
(при гибкости элемента
)
R>с> = 1,5 кН/см2 – расчетное сопротивление древесины сжатию;
Коэффициент а = 0,8 для древесины;
–
расчетное сопротивление древесины
смятию под углом;
R>см> = 1,5 кН/см2 – расчетное сопротивление древесины смятию вдоль волокон;
R>см.90> = 0,18 кН/см2 – расчетное сопротивление древесины смятию поперек волокон;
R>рα>= 0,9 кН/см2 – расчетное сопротивление древесины растяжению под углом;
Проверка прочности внутренней сжатой зоны
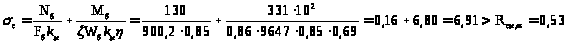
Проверка прочности биссектрисного сечения не проходит, следовательно увеличиваем сечение:
Ширина сечения b = 275 мм;
Размеры поперечного сечения рамы
h = 1000 мм, h>оп> = 300 мм, h>к >= 400 мм.
h>>> >= h/соs39о=100/0,777=130 см- высота биссектрисного сечения;
F>> = bh>> =27,5∙130=3575 см2- площадь биссектрисного сечения;
W>> =(bh>>2)/6 = 27,5∙1302/6= 77460 см3-расчетный момент сопротивления;
–
радиус инерции сечения;
- гибкость элемента цельного
сечения;
- коэффициент продольного изгиба
(при гибкости элемента
),
коэффициент а = 0,8 для древесины;
–
расчетное сопротивление древесины
смятию под углом;
Проверка прочности внутренней
сжатой зоны
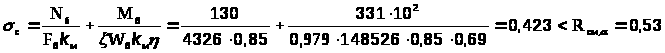кН/м2
Проверка прочности наружной растянутой зоны
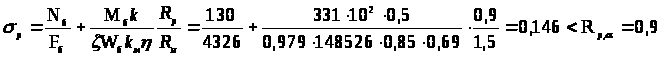кН/м2
Проверка прочности биссектрисного сечения выполняется
3.8 Проверка сечения рамы на устойчивость плоской формы деформирования
Проверку сечения рамы на устойчивость плоской формы деформирования производим по формуле
.
- для элементов, имеющих закрепление
из плоскости деформирования.
Сжатая грань арки имеет раскрепление панелями через 100см.
Определяем гибкость
.
.
.
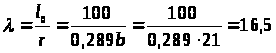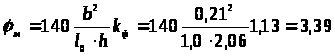Проверка
3.9 Проверка сечения арки на скалывание по клеевому шву
.
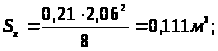
Проверка
Прочность сечения обеспечена.
3.10 Расчет опорного узла
Стойка в опорном узле опирается непосредственно на бетонный фундамент.
Для обеспечения возможности поворота опорного сечения торец стойки кантуется на 40 мм с каждой стороны. Стойка фиксируется металлическими уголками.
Места контакта древесины с бетоном изолируются двумя слоями рубероида, склеенными битумной мастикой.
1) Проверка на смятие вдоль волокон выполняется по формуле:
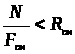
гдеN – усилие в стойке рамы, N = 130 кН;
F>см> – площадь смятия:
F>см> = b a = 21•36 = 756 см2;
R>см>= 1,5 кН/см2 – расчетное сопротивление древесины смятию вдоль волокон по табл. 3 [2]
Прочность на смятие вдоль волокон торца стойки выполняется.
2) Проверка на скалывание торца стойки от действия распора выполняется по формуле:
Где H = 83 кН – распор в раме от действия вертикальной нагрузки;
– статический момент инерции
сечения брутто;
–
момент инерции сечения брутто;
R>ск> = 0,07 кН/см2– расчетное сопротивление древесины скалыванию по табл. 3 [2]
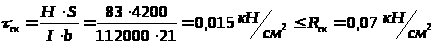
Прочность опорного узла на скалывание силой распора обеспечена.
Высота металлического башмака находится исходя из условия смятия поперек волокон древесины стойки рамы от действия распора
;
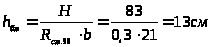Принимаем h=160мм;
Уголки, фиксирующие стойку поперечной рамы, принимаются из условия расположения болтов. Согласно табл. 39 [3]: минимальные расстояния от центра болта до края уголка должны быть не менее 1,5d = 1,5•16 = 24 мм.
Для обеспечения удобства монтажа принимаем уголок L160x12.
Крепление траверсы (уголков) башмака к фундаменту предусматриваем 2-мя болтами d = 24 мм.
Напряжение анкерного болта на срез:
=
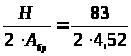= 9,2 кН/см2 <
R>ср>б
= 19 кН/см2;
Металлический башмак фиксируется в стойке рамы конструктивным болтом диаметром 16 мм.
3.11 Расчет конькового узла
Коньковый узел выполняют торцевым упором ветвей ригеля с перекрытием стыка двумя деревянными накладками на болтах.
Коньковый узел рассчитывается на поперечную силу при несимметричной односторонней снеговой нагрузки:
где S – расчетная нагрузка от веса снегового покрова на 1 пог. м ригеля рамы, определяется по формуле: S = 3,2∙1∙4,5 = 14,4 кН/м
ℓ – пролет ригеля, ℓ = 15 м;
;
Принимаем диаметр болтов, скрепляющих ригели рамы через накладки, 20 мм.
Накладка рассчитывается как балка на двух опорах.
Согласно п.5.18 [1] расстояния между осями болтов вдоль волокон древесины S>1>, поперек волокон S>2> и от кромки элемента S>3>:
S>1> = 7d = 7∙2 = 14 см;
S>2> = 3,5d = 3,5∙2 = 7 см;
S>3> = 3d = 3∙2 = 6 см;
;
;
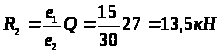Следовательно, более нагруженные болты расположены ближе к месту стыка.
Количество болтов в одном ряду определяется по формуле:
;
где n>c> – количество плоскостей среза, n>c> = 2;
[T]>б,>>min> – минимальная несущая способность одного болта, принимается согласно п.5.13 [1]:
1) Несущая способность на смятие древесины среднего элемента под углом α:
T>c> = 0,5 c d k>α>
здесьc – толщина среднего элемента, c = 21 см;
d – диаметр болта, d = 2 см;
k>α> – коэффициент, определяемый по табл. 19 [1]: k>α> = 0,981
T>c> = 0,5∙21∙2∙0,981 = 20,6 кН
2) Несущая способность на смятие древесины крайнего элемента под углом α:
T>a> = 0,8 a d k>α>
Здесь a – толщина крайнего элемента, a = 7,5 см;
T>a> = 0,8∙7,5∙2∙0,981 = 11,772 кН
3) Несущая способность болта на изгиб:
Несущая способность болта на изгиб не должна превышать величины:
Количество болтов в первом ряду:
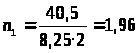
Принимаем 2 болта.
4. Меры защиты конструкций от загнивания и возгорания
При проектировании деревянной рамы из прямолинейных элементов предусматриваем конструктивные меры защиты от биологического разрушения, возгорания и действия химически агрессивной среды.
Конструктивные меры, обеспечивающие предохранение и защиту элементов от увлажнения, обязательны, независимо от того, производится антисептирование древесины или нет.
Конструктивные меры по предохранению и защите древесины от гниения обеспечивают:
устройство гидроизоляции от грунтовых вод, устройство сливных досок и козырьков для защиты от атмосферных осадков;
достаточную термоизоляцию, а при необходимости и пароизоляцию ограждающих конструкций отапливаемых зданий во избежание их промерзания и конденсационного увлажнения древесины;
систематическую просушку древесины в закрытых частях зданий путем создания осушающего температурно-влажностного режима (осушающие продухи, аэрация внутренних пространств).
Деревянные конструкции следует делать открытыми, хорошо проветриваемыми, по возможности доступными для осмотра.
Защита несущих конструкций:
В опорных узлах, в месте опирания рамы на фундамент устроить гидроизоляцию из двух слоев рубероида. При этом низ рамы запроектирован на отметке +0,2м. Торцы элементов рамы и места соприкосновения с металлическими накладками в опорном узле защитить тиоколовой мастикой У-30с с последующей гидроизоляцией рулонным материалом.
Для защиты от гигроскопического переувлажнения несущих конструкций через боковые поверхности необходимо покрыть пентафталевой эмалью ПФ-115 в два слоя.
Список используемой литературы
1. СНиП 2.01.07-85*. Нагрузки и воздействия. – М.:ГП ЦПП, 1996. - 44 с.
2. СНиП II-25-80. Деревянные конструкции. - М., 1983.
3. СНиП II-23-81. Стальные конструкции: М., 1990.
4. Рохлин И.А., Лукашенко И.А., Айзен А.М. Справочник конструктора-строителя. Киев, 1963, с. 192.
5. А..В. Калугин. Деревянные конструкции. Учеб. пособие (конспект лекций). - М.: Издательство АСВ, 2003.-224 с.