Сущность теории игр
Сущность теории игр
ПЛАН
ВВЕДЕНИЕ
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИГР
1.1 Основные понятия и критерии теории игр
1.2 Стратегии теории игр
1.2.1 Смешанные стратегии
1.2.2 Мажорирование (доминирование) стратегий
1.3 Игры с природой
2. ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ СМЕШАННЫХ СТРАТЕГИЙ
2.1 Постановка задачи
2.2 Описание алгоритма решения
ГЛАВА 3. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ИГР С ПРИРОДОЙ
3.1 Постановка задачи
3.2 Решение задач игр с природой
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
АННОТАЦИЯ
Тема курсового проекта, представленная в пояснительной записке, звучит как «Теория игр».
Объём данной пояснительной записки к курсовому проекту по дисциплине «Исследование операций» составляет 27 страниц, количество используемых источников 8.
Данная пояснительная записка содержит 3 (два) раздела, содержащих следующую информацию: теоретические основы теории игр, описание стратегий теории игр, а также описание практического применения указанных стратегий в исследовании операций.
ВВЕДЕНИЕ
На практике часто появляется необходимость согласования действий фирм, объединений, министерств и других участников проектов в случаях, когда их интересы не совпадают. В таких ситуациях теория игр позволяет найти лучшее решение для поведения участников, обязанных согласовывать действия при столкновении интересов. Теория игр все шире проникает в практику экономических решений и исследований. Ее можно рассматривать как инструмент, помогающий повысить эффективность плановых и управленческих решений. Это имеет большое значение при решении задач в промышленности, сельском хозяйстве, на транспорте, в торговле, особенно при заключении договоров с иностранными партнерами на любых уровнях. Так, можно определить научно обоснованные уровни снижения розничных цен и оптимальный уровень товарных запасов, решать задачи экскурсионного обслуживания и выбора новых линий городского транспорта, задачу планирования порядка организации эксплуатации месторождений полезных ископаемых в стране и др. Классической стала задача выбора участков земли под сельскохозяйственные культуры. Метод теории игр можно применять при выборочных обследованиях конечных совокупностей, при проверке статистических гипотез.
Обычно теорию игр определяют как раздел математики для изучения конфликтных ситуаций. Это значит, что можно выработать оптимальные правила поведения каждой стороны, участвующей в решении конфликтной ситуации.
В экономике, например, оказался недостаточным аппарат математического анализа, занимающийся определением экстремумов функций. Появилась необходимость изучения так называемых оптимальных минимаксных и максиминных решений. Следовательно, теорию игр можно рассматривать как новый раздел оптимизационного подхода, позволяющего решать новые задачи при принятии решений.
1.ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИГР
Основные понятия и критерии теории игр
Игра - упрощенная формализованная модель реальной конфликтной ситуации. Математически формализация означает, что выработаны определенные правила действия сторон в процессе игры: варианты действия сторон; исход игры при данном варианте действия; объем информации каждой стороны о поведении все других сторон.
Одну играющую сторону при исследовании операций может представлять коллектив, преследующий некоторую общую цель. Однако разные члены коллектива могут быть по-разному информированы об обстановке проведения игры.
Выигрыш или проигрыш сторон оценивается численно, другие случаи в теории игр не рассматриваются, хотя не всякий выигрыш в действительности можно оценить количественно.
Игрок - одна из сторон в игровой ситуации. Стратегия игрока - его правила действия в каждой из возможных ситуаций игры. Существуют игровые системы управления, если процесс управления в них рассматривается как игра.
Платежная матрица (матрица
эффективности, матрица игры) включает
все значения выигрышей (в конечной
игре). Пусть игрок 1 имеет т стратегий
А>i>,а
игрок 2 – n
стратегий B>j>>
>
 .
Игра может быть названа игрой т
n.
Представим матрицу эффективности игры
двух лиц с нулевой
суммой, сопроводив ее необходимыми
обозначениями (табл. 1.1).
.
Игра может быть названа игрой т
n.
Представим матрицу эффективности игры
двух лиц с нулевой
суммой, сопроводив ее необходимыми
обозначениями (табл. 1.1).
Таблица 1.1.
|
Игрок 2 Игрок 1 |
В>1> |
В>2> |
… |
В>n> |
>i> |
|
А>1> |
а>11> |
а>12> |
… |
а>1n> |
>1> |
|
А>2> |
a>21> |
a>22> |
… |
а>2n> |
>2> |
|
… |
… |
… |
… |
… |
… |
|
А>m> |
а>m1> |
а>m2> |
… |
а>mn> |
>m> |
|
>j> |
>1> |
>2> |
… |
>n> |
В данной матрице элементы а>ij>
- значения выигрышей игрока 1 - могут
означать математическое ожидание
выигрыша (среднее значение), если
выигрыш является случайной величиной.
Величины >i>, и
>j>,
и
>j>, – соответственно минимальные значения
элементов а>ij>
по строкам и максимальные - по столбцам.
Их содержательный смысл будет отражен
ниже.
– соответственно минимальные значения
элементов а>ij>
по строкам и максимальные - по столбцам.
Их содержательный смысл будет отражен
ниже.
В теории игр не существует установившейся классификации видов игр. Однако по определенным критериям некоторые виды можно выделить.
Количество игроков. Если в игре участвуют две стороны, то ее называют игрой двух лиц. Если число сторон больше двух, ее относят к игре п игроков. Наибольший интерес вызывают игры двух лиц. Они и математически более глубоко проработаны, и в практических приложениях имеют наиболее обширную библиографию.
Количество стратегий игры. По этому критерию игры делятся на конечные и бесконечные. В конечной игре каждый из игроков имеет конечное число возможных стратегий. Если хотя бы один из игроков имеет бесконечное число возможных стратегий, игра является бесконечной.
Взаимоотношения сторон. Согласно данному критерию игры делятся на кооперативные, коалиционные и бескоалиционные. Если игроки не имеют права вступать в соглашения, образовывать коалиции, то такая игра относится к бескоалиционным; если игроки могут вступать в соглашения, создавать коалиции - коалиционной. Кооперативная игра - это игра, в которой заранее определены коалиции.
Характер выигрышей. Этот критерий позволяет классифицировать игры с нулевой и с ненулевой суммой. Игра с нулевой суммой предусматривает условие: «сумма выигрышей всех игроков в каждой партии равна нулю». Игры двух игроков с нулевой суммой относят к классу антагонистических. Естественно, выигрыш одного игрока при этом равен проигрышу другого. Примерами игр с нулевой суммой служат многие экономические задачи. В них общий капитал всех игроков перераспределяется между игроками, но не меняется. К играм с ненулевой суммой также можно отнести большое количество экономических задач. Например, в результате торговых взаимоотношений стран, участвующих в игре, все участники могут оказаться в выигрыше. Игра, в которой нужно вносить взнос за право участия в ней, является игрой с ненулевой суммой.
Вид функции выигрышей. По этому критерию игры подразделяются на матричные, биматричные, непрерывные, выпуклые, сепарабельные и т.д. Поясним суть некоторых из них.
Матричная игра - конечная игра двух игроков с нулевой суммой. В общем случае ее платежная матрица является прямоугольной (см. табл. 1). Номер строки матрицы соответствует номеру стратегии, применяемой игроком 1. Номер столбца соответствует номеру стратегии игрока 2. Выигрыш игрока 1 является элементом матрицы. Выигрыш игрока 2 равен проигрышу игрока 1. Матричные игры всегда имеют решения в смешанных стратегиях. Они могут быть решены методами линейного программирования.
Биматричная игра - конечная игра двух игроков с ненулевой суммой. Выигрыши каждого игрока задаются своей матрицей, в которой строка соответствует стратегии игрока 1, а столбец - стратегии игрока 2. Однако элемент первой матрицы показывает выигрыш игрока 1, а элемент второй матрицы - выигрыш игрока 2. Для биматричных игр так же, как и для матричных, разработана теория оптимального поведения игроков.
Если функция выигрышей каждого игрока в зависимости от стратегий является непрерывной, игра считается непрерывной. Если функция выигрышей выпуклая, то и игра - выпуклая.
Если функция выигрышей может быть разделена на сумму произведений функций одного аргумента, то игра относится к сепарабельной.
Количество ходов. Согласно этому критерию игры можно разделить на одношаговые и многошаговые. Одношаговые игры заканчиваются после одного хода каждого игрока. Так, в матричной игре после одного хода каждого из игроков происходит распределение выигрышей. Многошаговые игры бывают позиционными, стохастическими, дифференциальными и др.
Информированность сторон. По данному критерию различают игры с полной и неполной информацией. Если каждый игрок на каждом ходу игры знает все ранее примененные другими игроками на предыдущих ходах стратегии, такая игра определяется как игра с полной информацией. Если игроку не все стратегии предыдущих ходов других игроков известны, то игра классифицируется как игра с неполной информацией. Мы далее убедимся, что игра с полной информацией имеет решение. Решением будет седловая точка при чистых стратегиях.
Степень неполноты информации. По этому критерию игры подразделяются на статистические (в условиях частичной неопределенности) и стратегические (в условиях полной неопределенности). Игры с природой часто относят к статистическим играм. В статистической игре имеется возможность получения информации на основе статистического эксперимента, при котором вычисляется или оценивается распределение вероятностей состояний (стратегий) природы. С теорией статистических игр тесно связана теория принятия экономических решений.
Получив некоторое представление о существующих подходах к классификации игр, можно остановиться на оценках игры.
Рассмотрим матричную игру,
представленную матрицей выигрышей mn,
где число строк i
=
 а число столбцов j
=
а число столбцов j
=
 (см. табл.1). Применим принцип получения
максимального гарантированного
результата при наихудших условиях.
Игрок 1 стремится принять такую стратегию,
которая должна обеспечить максимальный
проигрыш игрока 2. Соответственно игрок
2 стремится принять стратегию,
обеспечивающую минимальный выигрыш
игрока 1. Рассмотрим оба этих подхода.
(см. табл.1). Применим принцип получения
максимального гарантированного
результата при наихудших условиях.
Игрок 1 стремится принять такую стратегию,
которая должна обеспечить максимальный
проигрыш игрока 2. Соответственно игрок
2 стремится принять стратегию,
обеспечивающую минимальный выигрыш
игрока 1. Рассмотрим оба этих подхода.
Подход игрока 1. Он должен получить максимальный гарантированный результат при наихудших условиях. Значит, при выборе отвечающей этим условиям своей чистой стратегии он должен выбрать гарантированный результат в наихудших условиях, т.е. наименьшее значение своего выигрыша a>ij>, которое обозначим
.>i>>
>=
 .
(1.1)
.
(1.1)
Чтобы этот гарантированный эффект в наихудших условиях был максимальным, нужно из всех .>i>, выбрать наибольшее значение. Обозначим его и назовем чистой нижней ценой игры (максимин):
.>
>=
 (1.2)
(1.2)
Таким образом, максиминной стратегии отвечает строка матрицы, которой соответствует элемент а. Какие бы стратегии ни применял игрок 2, игрок 1 максиминной чистой стратегией гарантировал себе выигрыш не меньший, чем а. Таково оптимальное поведение игрока 1.
Подход игрока 2. Своими оптимальными стратегиями он стремится уменьшить выигрыш игрока 1, поэтому при каждой j -й чистой стратегии он отыскивает величину своего максимального проигрыша
( 1.3)
1.3)
в каждом j -м столбце, т.е. определяет максимальный выигрыш игрока 1, если игрок 2 применит j -ю чистую стратегию. Из всех своих п 7-х чистых стратегий он отыскивает такую, при которой игрок 1 получит минимальный выигрыш, т.е. определяет чистую верхнюю цену игры (минимакс):

Чистая верхняя цена игры показывает, какой максимальный выигрыш может гарантировать игрок 1, применяя свои чистые стратегии, - выигрыш, не меньший чем а. Игрок 2 за счет указанного выше выбора своих чистых стратегий не допустит, чтобы игрок 1 мог получить выигрыш, больший чем β. Таким образом, минимаксная стратегия отображается столбцом платежной матрицы, в котором находится элемент β (см. табл. 1). Она является оптимальной чистой гарантирующей стратегией игрока 2, если он ничего не знает о действиях игрока 1.
Чистая цена игры ν - цена данной игры, если нижняя и верхняя ее цены совпадают. В этом случае игра называется игрой с седловой точкой.
Стратегии теории игр
Смешанные стратегии
Если в матричной игре отсутствует седловая точка в чистых стратегиях, то находят верхнюю и нижнюю цены игры. Они показывают, что игрок 1 не получит выигрыша, превосходящего верхнюю цену игры, и что игроку 1 гарантирован выигрыш, не меньший нижней цены игры.
Смешанная стратегия игрока - это полный набор его чистых стратегий при многократном повторении игры в одних и тех же условиях с заданными вероятностями. Подведем итоги сказанного и перечислим условия применения смешанных стратегий:
• игра без седловой точки;
• игроки используют случайную смесь чистых стратегий с заданными вероятностями;
• игра многократно повторяется в сходных условиях;
• при каждом из ходов ни один игрок не информирован о выборе стратегии другим игроком;
• допускается осреднение результатов игр.
Применяются следующие обозначения смешанных стратегий.
Для игрока 1 смешанная стратегия, заключающаяся в применении чистых стратегий А>1>, А>2>, ..., А>т> с соответствующими вероятностями р>1>, р>2,> ..., р>т>.

где
 .
.
Для игрока 2

где
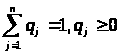 .
.
q>j> — вероятность применения чистой стратегии B>j>.
В случае когда р>i>> >= 1, для игрока 1 имеем чистую стратегию
 (1.7)
(1.7)
Чистые стратегии игрока являются
единственно возможными несовместными
событиями. В матричной игре, зная матрицу
А (она относится и к игроку 1, и к игроку
2), можно определить при заданных векторах
 и
и
 средний выигрыш (математическое ожидание
эффекта) игрока 1:
средний выигрыш (математическое ожидание
эффекта) игрока 1:
 (1.8)
(1.8)
где
 и
и
 –
векторы;
–
векторы;
p>i> и q>i> – компоненты векторов.
Путем применения своих смешанных стратегий игрок 1 стремится максимально увеличить свой средний выигрыш, а игрок 2 - довести этот эффект до минимально возможного значения. Игрок 1 стремится достигнуть
 (1.9)
(1.9)
Игрок 2 добивается того, чтобы выполнялось условие
 (1.10)
(1.10)
Обозначим
 и
и
 векторы, соответствующие оптимальным
смешанным стратегиям игроков 1 и 2, т.е.
такие векторы
векторы, соответствующие оптимальным
смешанным стратегиям игроков 1 и 2, т.е.
такие векторы
 и
и
 ,
при которых будет выполнено равенство
,
при которых будет выполнено равенство
 (1.11)
(1.11)
Цена игры - средний выигрыш игрока 1 при использовании обоими игроками смешанных стратегий. Следовательно, решением матричной игры является:
 –
оптимальная смешанная стратегия
игрока 1;
–
оптимальная смешанная стратегия
игрока 1;
 –
оптимальная смешанная стратегия
игрока 2;
–
оптимальная смешанная стратегия
игрока 2;
– цена игры.
Смешанные стратегии будут
оптимальными ( и
и
 ),
если образуют седловую
точку для функции
),
если образуют седловую
точку для функции т.е.
т.е.
 (1.12)
(1.12)
Существует основная теорема математических игр.
Для матричной игры с любой матрицей А величины
 и
и
 (1.13)
(1.13)
существуют и равны между собой: = = .
Следует отметить, что при выборе оптимальных стратегий игроку 1 всегда будет гарантирован средний выигрыш, не меньший чем цена игры, при любой фиксированной стратегии игрока 2 (и, наоборот, для игрока 2). Активными стратегиями игроков 1 и 2 называют стратегии, входящие в состав оптимальных смешанных стратегий соответствующих игроков с вероятностями, отличными от нуля. Значит, в состав оптимальных смешанных стратегий игроков могут входить не все априори заданные их стратегии.
Решить игру - означает найти цену игры и оптимальные стратегии. Рассмотрение методов нахождения оптимальных смешанных стратегий для матричных игр начнем с простейшей игры, описываемой матрицей 22. Игры с седловой точкой специально рассматриваться не будут. Если получена седловая точка, то это означает, что имеются невыгодные стратегии, от которых следует отказываться. При отсутствии седловой точки можно получить две оптимальные смешанные стратегии. Как уже отмечалось, эти смешанные стратегии записываются так:
 (1.14)
(1.14)
Значит, имеется платежная матрица
 (1.15)
(1.15)
При этом
a>11>p>1> + a>21>p>2> = ; (1.16)
a>12>p>1> + a>22>p>2> = ; (1.17)
p>1> + p>2> = 1. (1.18)
a>11>p>1> + a>21>(1 – p>1>) = a>12>p>1> + a>22>(1 – p>1>); (1.19)
a>11>p>1> + a>21> – a>21>p>1> = a>12>p>1> + a>22> – a>22>p>1>, (1.20)
откуда получаем оптимальные
значения и
и
 :
:
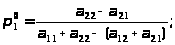 (1.21)
(1.21)
 (1.22)
(1.22)
Зная
 и
и
 ,
находим :
,
находим :
 (1.23)
(1.23)
Вычислив ,
находим
 и
и
 :
:
a>11>q>1> + a>12>q>2> = ; q>1> + q>2> = 1; (1.24)
a>11>q>1> + a>12 >(1 – q>1>) = . (1.25)
 при
a>11
>
a>12>.
(1.26)
при
a>11
>
a>12>.
(1.26)
Задача решена, так как найдены
векторы

 и цена игры .
Имея матрицу платежей А, можно решить
задачу графически. При этом методе
алгоритм решения весьма прост (рис.
2.1).
и цена игры .
Имея матрицу платежей А, можно решить
задачу графически. При этом методе
алгоритм решения весьма прост (рис.
2.1).
1. По оси абсцисс откладывается отрезок единичной длины.
2. По оси ординат откладываются выигрыши при стратегии А>1>.
3. На линии, параллельной оси ординат, в точке 1 откладываются выигрыши при стратегии a>2>.
4. Концы отрезков обозначаются для a>11>-b>11>, a>12>-b>21>, a>22>-b>22 >, a>21>-b>12> и проводятся две прямые линии b>11>b>12> и b>21>b>22>.
5. Определяется ордината точки пересечения с. Она равна . Абсцисса точки с равна р>2> (р>1> = 1 – р>2>).

Рис. 1.1. Оптимальная смешанная стратегия
Данный метод имеет достаточно
широкую область приложения. Это основано
на общем свойстве игр тп,
состоящем в том, что в любой игре тп
каждый игрок имеет оптимальную смешанную
стратегию, в которой число чистых
стратегий не больше, чем min(m,
n).
Из этого свойства можно получить
известное следствие: в любой игре 2п
и т2
каждая оптимальная стратегия
 и
и
 содержит не более двух активных стратегий.
Значит, любая игра 2п
и т2
может быть сведена к игре 22.
Следовательно, игры 2п
и т2
можно решить графически. Если матрица
конечной игры имеет размерность тп,
где т > 2 и п > 2, то для определения
оптимальных смешанных стратегий
используется линейное программирование.
содержит не более двух активных стратегий.
Значит, любая игра 2п
и т2
может быть сведена к игре 22.
Следовательно, игры 2п
и т2
можно решить графически. Если матрица
конечной игры имеет размерность тп,
где т > 2 и п > 2, то для определения
оптимальных смешанных стратегий
используется линейное программирование.
Мажорирование (доминирование) стратегий
Мажорирование представляет отношение между стратегиями, наличие которого во многих практических случаях дает возможность сократить размеры исходной платежной матрицы игры. Рассмотрим это понятие на примере матрицы:
 (1.27)
(1.27)
Рассуждая с позиции игрока 2, можно обнаружить преимущество его третьей стратегии перед второй, поскольку при первой стратегии игрока 1 выигрыш игрока 2 равен -3 (вторая стратегия) и 1 (третья стратегия), а при второй стратегии игрока 1 выигрыш игрока 2 равен -2 (вторая стратегия) и -0,5 (третья стратегия). Таким образом, при любой стратегии игрока 1 игроку 2 выгоднее применять свою третью стратегию по сравнению со второй; при наличии третьей стратегии игрок 2, если он стремится играть оптимально, никогда не будет использовать свою вторую стратегию, поэтому ее можно исключить из игры, т.е. в исходной платежной матрице можно вычеркнуть 2-й столбец:
 (1.28)
(1.28)
С позиции игрока 1 его первая стратегия оказывается хуже второй, так как по первой стратегии он только проигрывает. Поэтому первую стратегию можно исключить, а матрицу игры преобразовать к виду: (0 0,5).
Учитывая интересы игрока 2, следует оставить только его первую стратегию, поскольку, выбирая вторую стратегию, игрок 2 оказывается в проигрыше (0,5 - выигрыш игрока 1), и матрица игры принимает простейший вид: (0), т.е. имеется седловая точка.
Мажорирование можно распространить и на смешанные стратегии. Если элементы одной строки не все меньше (или равны) соответствующих элементов других строк, но все меньше (или равны) некоторых выпуклых линейных комбинаций соответствующих элементов других строк, то эту стратегию можно исключить, заменив ее смешанной стратегией с соответствующими частотами использования чистых стратегий.
В качестве иллюстрации к сказанному рассмотрим матрицу игры:
 (1.29)
(1.29)
Для первых двух чистых стратегий игрока 1 возьмем частоты их применения (вероятности) равными 0,25 и 0,75.
Третья стратегия игрока 1 мажорируется линейной выпуклой комбинацией первой и второй чистых стратегий, взятых с частотами 0,25 и 0,75 соответственно, т.е. смешанной стратегией:
24 0,25 + 0 0,75 = 6 > 4; (1.30)
0 0,25 + 8 0,75 = 6 > 5. (1.31)
Поэтому третью стратегию игрока 1 можно исключить, используя вместо нее указанную выше смешанную стратегию.
Аналогично, если каждый элемент некоторого столбца больше или равен некоторой выпуклой линейной комбинации соответствующих элементов некоторых других столбцов, то этот столбец можно исключить из рассмотрения (вычеркнуть из матрицы). Например, для матрицы
 (1.32)
(1.32)
третья стратегия игрока 2 мажорируется смешанной стратегией из первой и второй его чистых стратегий, взятых с частотами 0,5 и 0,5:
10 0,5 + 00,5 = 5 < 6; (1.33)
0 0,5 + 10 0,5 = 5 < 7. (1.34)
Таким образом, исходная матрица игры эквивалентна матрице следующего вида:
 (1.35)
(1.35)
Как видно, возможности мажорирования смешанными стратегиями в отличие от чистых значительно менее прозрачны (нужно должным образом подобрать частоты применения чистых стратегий), но такие возможности есть, и ими полезно уметь пользоваться.
1.3 Игры с природой
Модели в виде стратегических игр, в экономической практике могут не в полной мере оказаться адекватными действительности, поскольку реализация модели предполагает многократность повторения действий (решений), предпринимаемых в похожих условиях. В реальности количество принимаемых экономических решений в неизменных условиях жестко ограничено. Нередко экономическая ситуация является уникальной, и решение в условиях неопределенности должно приниматься однократно. Это порождает необходимость развития методов моделирования принятия решений в условиях неопределенности и риска.
Традиционно следующим этапом такого развития являются так называемые игры с природой. Формально изучение “игр с природой“, так же как и стратегических, должно начинаться с построения платежной матрицы, что является, по существу, наиболее трудоемким этапом подготовки принятия решения. Ошибки в платежной матрице не могут быть компенсированы никакими вычислительными методами и приведут к неверному итоговому результату.
Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игроком 1. Игрок 2 (природа) сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре. Поэтому термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально, хотя вполне могут встретиться ситуации, в которых «игроком» 2 действительно может быть природа (например, обстоятельства, связанные с погодными условиями или с природными стихийными силами).
2. ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ СМЕШАННЫХ СТРАТЕГИЙ
2.1 Постановка задачи
Выбрать оптимальный режим работы новой системы ЭВМ, состоящей из двух ЭВМ типов А>1> и А>2>. Известны выигрыши от внедрения каждого типа ЭВМ в зависимости от внешних условий, если сравнить со старой системой.
При использовании ЭВМ типов А>1> и А>2> в зависимости от характера решаемых задач В>1> и В>2> (долговременные и краткосрочные) будет разный эффект. Предполагается, что максимальный выигрыш соответствует наибольшему значению критерия эффекта от замены вычислительной техники старого поколения на ЭВМ A>1> и А>2>.
Итак, дана матрица игры (табл. 1), где A>1>, А>2> - стратегии руководителя; В>1, >В>2> - стратегии, отражающие характер решаемых на ЭВМ задач.
Таблица 2.1.
|
Игрок 2 Игрок 1 |
В>1> |
В>2> |
>i> |
|
А>1> |
0,3 |
0,8 |
0,3 |
|
А>2> |
0,7 |
0,4 |
0,4 |
|
>j> |
0,7 |
0,8 |
Требуется найти оптимальную смешанную стратегию руководителя и гарантированный средний результат , т.е. определить, какую долю времени должны использоваться ЭВМ типов A>1> и А>2>.
2.2 Описание алгоритма решения
Запишем условия в принятых обозначениях:
а>11> = 0,3; а>12> = 0,8; а>21> = 0,7; а>22> = 0,4.
Определим нижнюю и верхнюю цены игры:
>1> = 0,3; >2> = 0,4; = 0,4; >1>=0,7; >2> = 0,8; = 0,7.
Получаем игру без седловой точки, так как
 (2.1)
(2.1)
 (2.2)
(2.2)
Максиминная стратегия руководителя вычислительного центра – А>2>.
Для этой стратегии гарантированный выигрыш равен = 0,4 (40%) по сравнению со старой системой.
Определим , p>l> и р>2> графическим способом (рис. 2.1).

Рис. 2.1. Графическая интерпретация алгоритма решения
Алгоритм решения:
1. По оси абсцисс отложим отрезок единичной длины.
2. По оси ординат отложим выигрыши при стратегии А>1>.
3. На вертикали в точке 1 отложим выигрыши при стратегии А>2>.
4. Проводим прямую b>11>b>12>, соединяющую точки а>11>, а>21>.
5. Проводим прямую b>21>b>22>, соединяющую точки а>12>, а>22>.
6. Определяем ординату точки пересечения с линий b>11>b>12> и b>21>b>22>. Она равна .
7. Определим абсциссу точки пересечения с. Она равна р>2>, а р>1 >= l – р>2. >
Выпишем решение и представим оптимальную стратегию игры:
р>1> = 0,375; (2.3)
р>2> =
0,625;
 (2.4)
(2.4)
=0,55. (2.5)
Вывод. При установке новой системы ЭВМ, если неизвестны условия решения задач заказчика, на работу ЭВМ А>1> должно приходиться 37,5% времени, а на работу ЭВМ А>2> - 62,5%. При этом выигрыш составит 55% по сравнению с предыдущей системой ЭВМ.
3. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ИГР С ПРИРОДОЙ
3.1 Постановка задачи
Рассмотрим игры с природой на примере следующей задачи. Необходимо закупить уголь для обогрева дома. Количество хранимого угля ограничено и в течение холодного периода должно быть полностью израсходовано. Предполагается, что неизрасходованный зимой уголь в лето пропадает. Покупать уголь можно в любое время, однако летом он дешевле, чем зимой. Неопределенность состоит в том, что не известно, какой будет зима: суровой, тогда придется докупать уголь, или мягкой, тогда часть угля может остаться неиспользованной. Очевидно, что у природы нет злого умысла и она ничего против человека «не имеет». С другой стороны, долгосрочные прогнозы, составляемые метеорологическими службами, неточны и поэтому могут использоваться в практической деятельности только как ориентировочные при принятии решений.
Имеются следующие данные о количестве и ценах угля, необходимого зимой для отопления дома (табл. 3.1). Вероятности зим: мягкой - 0,35; обычной - 0,5; холодной - 0,15.
|
Зима |
Количество угля, т |
Средняя цена за 1 т, грн. |
|
Мягкая |
4 |
7 |
|
Обычная |
5 |
7,5 |
|
Холодная |
6 |
8 |
Эти цены относятся к покупкам угля зимой. Летом цена угля 6 грн. за 1 т. Есть место для хранения запаса угля до 6 т, заготавливаемого летом. Если потребуется зимой докупить недостающее количество угля, докупка будет по зимним ценам. Предполагается, что весь уголь, который сохранится до конца зимы, в лето пропадет. (Предположение делается для упрощения постановки и решения задачи.)
Сколько угля летом покупать на зиму?
3.2 Решение задач игр с природой
Пользуясь исходными данными, строим матрицу игры. Стратегиями игрока 1 (человек) являются различные показатели количества тонн угля, которые ему, возможно, следует купить. Состояниями природы выступают вероятности видов зимы.
Вычислим, например, показатель для холодной зимы. Игрок 1 приобрел уголь для обычной зимы 5 т по цене 6 грн. за 1 т. Для обогрева он должен закупить еще 1 тонну по цене 8 грн за 1т.
Следовательно, расчет платы за уголь будет 5 6 – при заготовке, и зимой 8 1. Аналогично производятся расчеты при других сочетаниях.
В итоге получим следующую платежную матрицу в игре с природой платежную матрицу (табл. 3.2).
Таблица 3.2.
|
Вероятность Зима |
0,35 |
0,5 |
0,15 |
|
Мягкая |
Обычная |
Холодная |
|
|
Мягкая (4т) |
-(4 6) |
-(4 6 + 1 7,5) |
-(4 6 + 2 8) |
|
Обычная (5 т) |
-(5 6) |
-(5 6 + 0 7,5) |
-(5 6 + 1 8) |
|
Холодная (6 т) |
-(6 6) |
-(6 6 + 0 7,5) |
-(6 6 + 0 8) |
Произведем расчет ожидаемой средней платы за уголь (табл. 3.3).
Таблица 3.3
|
Зима |
Средняя ожидаемая плата |
|
Мягкая |
-(24 0,35 + 31,5 0,5 + 40 0,15) = -30,15 |
|
Обычная |
-(30 0,35 + 30 0,5 + 38 0,15) = -31,2 |
|
Холодная |
-(36 0,35 + 36 0,5 + 36 0,15) = - 36 |
Как видно из табл. 3.3, наименьшая ожидаемая средняя плата приходится на случай мягкой зимы (30,15 грн.). Соответственно если не учитывать степени риска, то представляется целесообразным летом закупить 4 т угля, а зимой, если потребуется, докупить уголь по более высоким зимним ценам.
Однако, привлекая дополнительную информацию в форме расчета среднеквадратичного отклонения как индекса риска. Мы можем уточнить принятое на основе максимума прибыли или минимума издержек решение. Дополнительные рекомендации могут оказаться неоднозначными, зависящими от склонности к риску ЛПР.
Формулы теории вероятности:
Дисперсия случайной величины ξ равна


Среднеквадратичное отклонение составит
где D и М - соответственно символы дисперсии и математического ожидания.
Проводя соответственно вычисления для всех случаев по такому принципу:
Мягкая зима:
М(ξ2) = - (242 0,35 + 31,52 0,5 + 402 0,15) = - 937,725
(Мξ)2 = -(30,152 ) = - 909,0225
Dξ =937,725- 909,0225 = 28,7025
= 5,357
Если продолжить исследование процесса принятия решения и вычислить среднеквадратичные отклонения платы за уголь для мягкой, обычной и холодной зимы, то соответственно получим:
• для мягкой зимы = 5,357;
• для обычной зимы = 2,856;
• для холодной зимы = 0.
Минимальный риск, естественно, будет для холодной зимы, однако при этом ожидаемая средняя плата за уголь оказывается максимальной - 36 ф. ст.
Вывод. Мы склоняемся к варианту покупки угля для обычной зимы, так как ожидаемая средняя плата за уголь по сравнению с вариантом для мягкой зимы возрастает на 3,5%, а степень риска при этом оказывается почти в 2 раза меньшей ( = 2,856 против 5,357).
Отношение среднеквадратичного отклонения к математическому ожиданию, вариабельность (средний риск на затрачиваемый 1 ф. ст.) для обычной зимы составляет 2,856/31,2 = 0,0915 против аналогичного показателя для мягкой зимы, равного 5,357/30,15 = 0,1777, т.е. вновь различие почти в 2 раза.
Эти соотношения и позволяют рекомендовать покупку угля, ориентируясь не на мягкую, а на обычную зиму.
ЗАКЛЮЧЕНИЕ
В заключение данной работы можно сделать вывод о необходимости использования теории игр в современных экономических условиях.
В условиях альтернативы (выбора) очень часто нелегко принять решение и выбрать ту или иную стратегию. Исследование операций позволяет с помощью использования соответствующих математических методов принять обоснованное решение о целесообразности той или иной стратегии. Теория игр, имеющая в запасе арсенал методов решения матричных игр, позволяет эффективно решать указанные задачи несколькими методами и из их множества выбрать наиболее эффективные, а также упрощать исходные матрицы игр.
В данной работе были проиллюстрированы практическое применение двух основных стратегий теории игр и сделаны соответствующие выводы.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Тернер Д. Вероятность, статистика, исследование операций: Пер. с англ. – М.: Высш.шк., 1971.
Мак Киси Дж. Введение в теорию игр: Пер. с англ. – М.: Физматгиз, 1960.
Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение: Пер. с англ. – М.: Наука, 1970.
Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: ДИС, 1997.
Дубров А.М. Математико-статистическая оценка эффективности в экономических задачах. – М.: Финансы и статистика, 1982.
Дубров А.М. Последовательный анализ в статистической обработке информации. – М.: Статистика, 1976.
Вальд А. Последовательный анализ: Пер. с англ. – М.: Физматгиз, 1960.
Моделирование рисковых ситуаций в экономике и бизнесе: Учеб. пособие /А.М. Дубров, Б.А. Лагоша, Е.Ю. Хрусталев, Т.П. Барановская; Под ред. Б.А. Лагоши. – 2-е изд., пере раб. и доп. – М.: Финансы и статистика, 2001.