Решение задач на переливание на бильярдном столе

III научно-практическая конференция школьников

по математике, её приложениям и информационным технологиям

Поиск

Учебно-исследовательская работа

Гомель, 2008

Содержание

Введение

1. Математическая модель бильярда

2. Траектории движения

3. Задачи на переливание

3.1 Типичные задачи на переливание

3.2 Условие разрешимости задач

3.3 Алгоритм решения задач на переливание

Заключение

Список использованных источников

Приложение

Введение

В данной работе изучаются так называемые бильярдные системы. К простейшим из них относятся «бильярд в плоской области» (точечный шар, движущийся внутри круга, прямоугольника, эллипса, многоугольника и т. д.) и «одномерный бильярд». Общим свойством бильярдных систем является закон абсолютно упругого отражения. О геометрических, «арифметических», физических следствиях этого закона и рассказывается в работе.

Подобно тому, как азартная игра в кости вызвала к жизни «исчисление» вероятностей, игра в бильярд послужила предметом серьезных научных исследований по механике и математике. Описанию движения бильярдного шара (с учетом трения) на прямоугольном столе с лузами посвящена книга известного французского физика Г.Г. Кориолиса, написанная им в 1835 г. за год до избрания его академиком Парижской академии наук.

Методы исследования бильярдных систем (например, анализ поведения бильярдных траекторий), с одной стороны, примыкают к традиционной геометрии, а с другой — лежат на стыке отраслей современной математики — теории чисел, топологии, эргодической теории и теоретической механики. Будучи, как правило, вполне элементарными, эти методы позволяют получить далеко не элементарные выводы.

Общая математическая проблема бильярда заключается в том, чтобы описать возможные типы бильярдных траекторий в данной области Q. Простейший принцип такого описания — разделение траекторий на периодические, или замкнутые, и остальные — непериодические.

Интерес представляют и такие вопросы: Какое число звеньев может иметь периодическая траектория? Какие периоды имеют периодические траектории в данной области (если принять минимальный период периодической траектории, скажем, за единицу)?

Оказывается, это далеко не праздные вопросы — например, они имеют прямое отношение к исследованию специальных систем квантовой механики.

Многие результаты являются классическими и восходят к Кориолису, Больцману, Пуанкаре, Киркгофу. Современная теория бильярдов является одним из актуальных направлений математической физики. Ее основы были заложены советским математиком Я. Г. Синаем и его школой.

В первом разделе данной работы описана математическая модель бильярда.

Во втором разделе описаны виды траекторий бильярного шара.

В третьем разделе описаны задачи на «переливание» и их решение с помощью математической модели бильярда.

1. Математическая модель бильярда

Представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов. Спрашивается, какой может быть траектория этого шарика?

Математическая проблема бильярда, или проблема траекторий, состоит в том, чтобы найти ответ на этот вопрос. Описанная механическая система — точечный шар в бильярдной области Q, ограниченной бортом Г (границей области Q),— и называется математическим бильярдом. Траектория бильярда в области Q определяется начальным положением точки q () и начальным вектором ее скорости . Пренебрежение трением означает, что абсолютную величину скорости при движении точки мы считаем неизменной во времени, поэтому задаваемый в начальный момент времени t=0 вектор можно считать единичным, характеризующимся лишь своим направлением. Направление вектора (t), т. е. направление движения шара, меняется только при его ударе о борт. Это происходит по закону абсолютно упругого отражения: после удара шара (точки q(t)) о борт Г в точке P шар движется так, что его «угол падения равен углу отражения». Если борт Г в окрестности точки P криволинейный, то углы падения и отражения — это углы, составленные «падающим» и «отраженным» отрезками траектории с касательной MN к кривой Г, проведенной в точке P. Таким образом, траектория бильярда — это вписанная в кривую Г ломаная, которая может быть однозначно построена по своему начальному звену.

2. Траектории движения

Траектория с «начальным условием» будет периодической (или замкнутой), если через некоторое время (через период), точка возвращается в свое начальное положение q с первоначальной скоростью .

Периодические движения воспринимаются как наиболее «правильные» — такими мы привыкли представлять, например, движения планет около Солнца и качания маятника. Рассматриваемая проблема в отношении периодических траекторий сводится, в частности, к вопросу о существовании: в любой ли области Q существуют периодические (замкнутые) траектории? Другой вопрос — о критерии периодичности: как по данным начальным условиям узнать, будет ли соответствующая траектория периодической?

Теорема [Биркгоф]. У бильярда в любой выпуклой области Q на плоскости, ограниченной замкнутой гладкой кривой Г, существуют периодические бильярдные траектории с любым числом звеньев .

3. Задачи на переливание

3.1. Типичные задачи на переливание

В задачах на переливания требуется указать последовательность действий, при которой осуществляется требуемое переливание и выполнены все условия задачи. Если не сказано ничего другого, считается, что

все сосуды без делений
нельзя переливать жидкости "на глаз"
невозможно ниоткуда добавлять жидкости и никуда сливать.

Мы можем точно сказать, сколько жидкости в сосуде, только в следующих случаях.

знаем, что сосуд пуст,
знаем, что сосуд полон, а в задаче дана его вместимость,
в задаче дано, сколько жидкости в сосуде, а переливания с использованием этого сосуда не проводились
в переливании участвовали два сосуда, в каждом из которых известно, сколько было жидкости, и после переливания вся жидкость поместилась в один из них
в переливании участвовали два сосуда, в каждом из которых известно, сколько было жидкости, известна вместимость того сосуда, в который переливали, и известно, что вся жидкость в него не поместилась: мы можем найти, сколько ее осталось в другом сосуде

Приведем типичные задачи на переливание.

Задача 1. Имеются три сосуда вместимостью 8, 5 и 3 литра. Наибольший сосуд полон молока. Как разделить это молоко на две равные части, используя остальные сосуды?

Решение.

В таблице указан объем молока в литрах после каждого переливания.

8-литровый сосуд	5-литровый сосуд	3-литровый сосуд
8	0	0
3	5	0
3	2	3
6	2	0
6	0	2
1	5	2
1	4	3
4	4	0

После переливания оказалось по 4 л молока в 8-литровом и 5-литровом сосудах, а это и требовалось.

Задача 2. В бочке не менее 10 л бензина. Как отлить из неё 6 л с помощью девятилитрового ведра и пятилитрового бидона?

Решение.

В таблице указан объем бензина в литрах после каждого переливания.

бочка	ведро	бидон
не менее 10	0	0
не менее 5	0	5
не менее 5	5	0
не менее 0	5	5
не менее 0	9	1
не менее 9	0	1
не менее 9	1	0
не менее 4	1	5
не менее 4	6	0

Задача 3. Имеется три сосуда без делений объемами 4 л, 5 л, 6 л, кран с водой, раковина и 4 л сиропа в самом маленьком сосуде. Можно ли с помощью переливаний получить 8 л смеси воды с сиропом, так чтобы в каждом сосуде воды и сиропа было поровну?

Решение

4-литровый сосуд	5-литровый сосуд	6-литровый сосуд
4 л сиропа	0	0
0	4 л сиропа	0
4 л воды	4 л сиропа	0
0	4 л сиропа	4 л воды
4 л воды	4 л сиропа	4 л воды
2 л воды	4 л сиропа	6 л воды
2 л воды	4 л сиропа	0
2 л воды, 2 л сиропа	2 л сиропа	0
2 л воды, 2 л сиропа	0	2 л сиропа
0	2 л воды, 2 л сиропа	2 л сиропа
2 л сиропа	2 л воды, 2 л сиропа	0
2 л воды, 2 л сиропа	2 л воды, 2 л сиропа	0

По сути, в данных задачах реализуются два алгоритма.

Первый: последовательно из большего сосуда наполняется меньший сосуд, из него жидкость сливается в сосуд промежуточного объема, эти два действия повторяются до полного наполнения сосуда промежуточного объема, после чего жидкость из него сливается в самый большой. Процедура повторяется несколько раз до тех пор, пока два меньших сосуда будут пустыми, а вся жидкость окажется в большом сосуде. Таким образом, будут реализованы все возможные варианты наполнения сосудов.

Второй алгоритм соответствует действиям первого, записанным в обратном порядке, т.е. с конца. Сначала из большего сосуда наполняется сосуд промежуточного объема. Из него жидкость переливается в самый маленький, а из наименьшего - в наибольший. Два последних действия повторяются до тех пор, пока сосуд промежуточного объема не станет пустым. Тогда он наполняется жидкостью из самого большого сосуда. Эта процедура повторяется до возвращения к исходному состоянию.

Решение задачи можно получить и по первому и по второму алгоритму, выбирается более короткий вариант.

3.2 Условие разрешимости задач

Если объемы двух меньших сосудов не имеют общего делителя (т. е. взаимно просты), а объем третьего сосуда больше или равен сумме объемов двух меньших, то с помощью этих трех сосудов можно отмерить любое целое число литров, начиная с 1 литра и кончая объемом среднего сосуда.

Имея, например, сосуды вместимостью 15, 16 и 31 литр, вы сумеете отмерить любое количество воды от 1 до 16 литров. Такая процедура невозможна, если объемы двух меньших сосудов имеют общий делитель.

3.3 Алгоритм решения задач на переливание

Рассмотри задачу: как с помощью сосудов объемом 7 и 11 литров и бочкой с водой отмерить 2 литра воды.

Как ни странно, но головоломки на переливание жидкостей можно очень легко решать, вычерчивая бильярдную траекторию шара, отражающегося от бортов ромбического стола! Границы таких столов удобнее всего рисовать на бумаге, на которую нанесена сетка из одинаковых равносторонних треугольников. В рассматриваемой задаче стороны стола должны иметь длины 7 и 11 единиц (рисунок 1).

По горизонтали отложено количество воды в 11-литровом сосуде в любой момент времени, а по вертикали — та же величина для 7-литрового сосуда.

Как же пользоваться диаграммой? Представьте себе, что шар находится в левой нижней вершине в точке 0. Он будет перемещаться вдоль нижнего основания ромба до тех пор, пока не достигнет правой боковой стороны в точке 11. Это означает, что 11-литровый сосуд наполнен до краев, а 7-литровый пуст.

Отразившись упруго от правого борта, шар покатится вверх и влево и ударится о верхний борт в точке с координатами 4 по горизонтали и 7 по вертикали. Это означает, что в 11-литровом сосуде осталось всего 4 литра воды, а 7 литров из него перелили в меньший сосуд.

Прослеживая дальнейший путь шара и записывая все этапы его движения до тех пор, пока он не попадет в точку 2 верхнего борта, вы получите ответ и узнаете, в какой последовательности необходимо производить переливания, чтобы отмерить 2 литра воды. Все 18 переливаний изображены схематически на рис. 1. Наклонные стрелки говорят о том, что вода переливается из одного сосуда в другой, а вертикальные означают, что либо вода целиком выливается из меньшего сосуда обратно в бочку, либо больший сосуд надо наполнить водой до краев.

Является ли это решение самым коротким? Нет, существует второй путь, когда воду сначала наливают в 7-литровый сосуд. На диаграмме (рис. 1) это соответствует тому, что шар из точки 0 катится вверх вдоль левого борта до тех пор, пока не ударится в верхний борт. Нарисовав траекторию бильярдного шара, читатель убедится в том, что точка 2 достигается на этот раз за 14 отражений от борта. Полученное решение с 14 переливаниями уже является самым коротким.

Требуется немного сообразительности, чтобы применить метод бильярдного шара к любой задаче о переливании жидкости с помощью не более чем трех сосудов.

Рассмотрим старую головоломку с тремя сосудами, восходящую еще к Никола Фонтана, итальянскому математику XVI века. Восьмилитровый сосуд до краев наполнен водой. С помощью двух пустых сосудов объемом 3 и 5 литров воду надо поровну разлить в два больших сосуда. Диаграмма для этой задачи — ромбический стол размером 3х5 --- изображена на рис. 2. Главная диагональ рома поделенная наклонными прямыми на 8 частей, относится к 8-литровому сосуду. Как и в предыдущей задаче, бильярдный шар начинает свое движение из точки 0.

Нарисовать его траекторию совсем несложно. С ее помощью вы получите решение в минимальным числом переливаний, равным 7.

Когда объем большего сосуда меньше суммы объемов двух других, возникают новые ограничения. Если, например, объемы сосудов равны 7, 9 и 12 литрам, то у ромбического стола надо отсечь нижний правый угол (рис. 3). Тогда шар сможет попасть в любую точку от 1 до 9, за исключением точки 6. Несмотря на то, что 7 и 9 взаимно просты, отмерить 6 литров воды оказывается невозможным из-за того, что самый большой сосуд имеет слишком маленький объем.

заключение

В данной работе рассмотрена математическая модель бильярда и связанные с этой моделью понятия периодичности тракторий. Данная модель неожиданно много имеет применений в теории чисел, механике, физике и арифметике.

Наиболее подробно было исследовано применение данной модели в задачах исследования операций, а именно, в, так называемых, задачах на переливание. Приведены модели таких задач, условия разрешимости и алгоритмы решения, как арифметическим способом, так и с помощью рассматриваемой модели.

Рассматриваемые задачи традиционно встречаются на олимпиадах по математике различного уровня, и, несомненно, данная работа будет отличным подспорьем, для желающих научится решать данные задачи.

К сожалению, не были рассмотрены конкретные применения данной модели в различных областях науки. Но это планируется исправить в дальнейшем.

Список использованных источников

1. Гальперин Г.А., Математические бильярды [текст]/ Земляков А.Н., Гальперин Г.А — М.: Наука,- 1990.- 290с.

2. Кориолис Г.Г., Математическая теория явлений бильярдной игры. [текст]/ Кориолис Г. Г.— М.: Гостехиздат, 1956.

3. Борахеостов В., Бильярды [текст]/ Борахеостов В. // Наука и жизнь. 1966. №№ 2-4, 6, 11.

Гальперин Г.А., Бильярды [текст] / Гальперин Г.А. //Квант. 1981. №4.
Земляков А.Н., Математика бильярда [текст]/ Земляков А.Н. // Квант. 1976. № 5.
Земляков А.Н., Арифметика и геометрия столкновений [текст]/ Земляков А.Н. // Квант. 1978. №4.
Земляков А.Н., Бильярды и поверхности [текст]/ Земляков А. Н. // Квант. 1979. № 9.
Гальперин Г.А., Периодические движения бильярдного шара [текст]/ Гальперин Г.А., Степин А. М.// Квант. 1989. № 3.
Тихомиров В.М., Рассказы о максимумах и минимумах [текст]/ Тихомиров В.М.— М.: Наука, 1986 (Библиотечка "Квант". Вып. 56).

Приложение

Рисунок 1

Рисунок 2

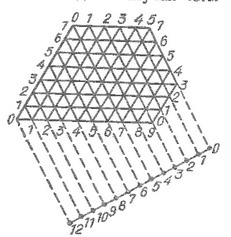
Рисунок 3