Разработка программных средств анализа графика функции и решение оптимизационных задач

СОДЕРЖАНИЕ

Введение

1 Введение в Microsoft Excel

2 Основные функции в Microsoft Excel

3 Формулы в Microsoft Excel

4 Общие сведения об алгоритмах

5 Метод половинного деления

6 Решение задачи

7 Понятие оптимизационных задач и оптимизационных моделей

8 Решение задачи

Заключение

Приложение А

Приложение Б

Приложение В

Приложение Г

Приложение Д

ВВЕДЕНИЕ

Задачи, требующие оптимизации, встречаются в самых различных сферах человеческой деятельности, так как на их решении базируется принятие решений. Всегда люди, приступая к реализации своих действий, раздумывали над их возможными последствиями и принимали решения, выбирая тем или другим образом способы осуществления конкретных мероприятий. Каждое разумное действие является в определенном смысле и оптимальным, ибо оно, как правило, выбирается после сравнения с другими вариантами.

В связи со сложностью прикладных оптимизационных задач принятие решений в них все в меньшей мере стало основываться на «здоровом смысле», интуиции и опыте человека. Необходим научный подход, базирующийся на математическом описании решаемых проблем.

Первые задачи по изучению экстремальных свойств геометрических фигур (круг, квадрат и т.д.) были решены еще в древние века. Мощным толчком к развитию методов оптимизации послужило создание дифференциального и интегрального исчислений. В течение короткого промежутка времени были созданы новые разделы теории (линейное программирование, теория оптимального управления и т. д.), которые привели к разработке ряда эффективных численных методов решения разнообразных экстремальных задач.

В настоящее время для решения сложных статистических, коммерческих, научных и инженерных задач используют компьютер, который позволяет решать задачи со многими переменными. Входящий в наиболее широко распространенный программный пакет Microsoft Office табличный процессор Excel располагает средствами для решения широкого круга задач оптимизации:

Ассортимент продукции. Максимизация выпуска товаров при ограничениях на сырье для производства этих товаров.

Штатное расписание. Составление штатного расписания для достижения наилучших результатов при наименьших расходах.

Планирование перевозок. Минимизация затрат на транспортировку товаров.

Составление смеси. Достижение заданного качества смеси при наименьших расходах.

1 ВВЕДЕНИЕ В Microsoft Excel

Любой вид деятельности требует систематизации хранимых данных. С расширением перечня продуктов, услуг и клиентов любому бизнесу необходима комплексная система для хранения большого объема финансовой и другой документации.

Microsoft Excel – это программа, предназначенная для организации данных в таблицы для документирования, сопоставления и графического представления информации. Например, можно использовать Excel для суммирования, вычисления среднего или максимального числа продаж за день; создание графика, показывающего определенный процент продаж, сравнения общего объема продаж за день с тем же показателем других дней недели. Excel освобождает от проведения этих вычислений вручную.

При запуске Excel появляется пустой документ. С этого момента можно вводить информацию, изменять оформление данных, обрабатывать данные или искать информацию в файлах справки Excel

Главной составной частью документа Microsoft Excel является поле, которое содержит определенную информацию. В Excel это поле называется ячейкой. Каждая ячейка находится на пересечении строки (горизонтальной последовательности ячеек) и столбцов (вертикальной последовательности ячеек); строки обозначены числами, а столбцы – буквами. Номер строки и буква столбца, обозначающие определенную ячейку, называется ссылкой на ячейку.

Рабочий лист состоит из набора строк и столбцов и представляет страницу в документе Excel. Рабочей книгой называется один или несколько рабочих листов. Создавая документ Excel, создается рабочая книга с тремя рабочими листами.

2 ОСНОВНЫЕ ФУНКЦИИ В Microsoft Excel

функции – это специально созданные формулы для обработки данных. Программа Excel имеет сотни встроенных функций, которые предназначены для проведения самых разнообразных вычислений. Многие из этих функций нам и никогда и не понадобятся. Здесь есть как достаточно простые функции, например, тригонометрические, так и весьма сложные, например, функции для определения стандартного отклонения или для проведения статистического анализа.

Работая в Excel, почти всегда можно найти подходящую функцию, которая предназначена для решения самых разнообразных вычислительных задач. Эти функции разделены на следующие категории:

финансовые;

дата и время;

математические;

статистические;

ссылки и массивы;

работа с базой данных;

текстовые;

логические;

инженерные.

Каждая функция имеет один или несколько аргументов. Аргументом называются значения, с которыми оперирует функция. В зависимости от формулы аргументом могут быть ссылка на ячейку, имя ячейки, диапазон ячеек, число, логическое значение или текст. У некоторых функций нет аргумента (например, функция ПИ).

Логические функции это функции типа если, и, не, истина, ложь. Эти функции используются для проверки условий и для определения, является ли то или иное утверждение истинным или ложным. Для оценки логических условий используются функции если, и, или, не.

Логические условия, формулы или функции могут возвращать значения истина или ложь. Логическое условие может быть либо правдой, либо ложью.

Функция ИЛИ возвращает ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА; возвращает ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ.

Функция НЕ меняет на противоположное значение своего аргумента. Если аргумент имеет значение ИСТИНА, функция НЕ возвращает значение ЛОЖЬ и наоборот.

С помощью функции ЕСЛИ можно оценить до 30 логических условий и возвратить различные числовые или текстовые значения, в зависимости от того, будут ли логические условия истинными или ложными.

В Microsoft Excel имеется только одна категория математических функций, но для удобства рассмотрения ее можно разбить на три типа:

арифметические функции;

алгебраические функции;

тригонометрические функции.

Арифметические функции используют такие математические действия, как сложение, вычитание, умножение и деление.

Алгебраические функции позволяют вычислять логарифмы, экспоненты, квадратные корни и другие.

Тригонометрические функции позволяют вычислить синусы, косинусы, тангенсы и так далее.

3 ФОРМУЛЫ В MICROSOFT EXCEL

Формулы представляют собой выражения, по которым выполняются вычисления на странице. Формула начинается со знака равенства (=).

Формула также может включать следующие элементы:

функции;

ссылки;

операторы (знак или символ, задающий тип вычисления в формуле. Существуют математические, логические операторы, операторы сравнения и ссылок);

константы (постоянное (не вычисляемое) значение).

Ссылка указывает на ячейку или диапазон ячеек листа и передает в Microsoft Excel сведения о расположении значений или данных, которые требуется использовать в формуле. При помощи ссылок можно использовать в одной формуле данные, находящиеся в разных частях листа, а также использовать в нескольких формулах значение одной ячейки. Кроме того, можно задавать ссылки на ячейки других листов той же книги и на другие книги. Ссылки на ячейки других книг называются связями.

Существуют относительные, абсолютные и смешанные ссылки.

Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейку, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка.

Абсолютная ссылка ячейки в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется.

Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка столбцов приобретает вид $A1, $B1 и т. д. Абсолютная ссылка строки приобретает вид A$1, B$1 и т. д.

4 Общие сведения об алгоритмах.

Алгоритм – предписание последовательности действий, направленных на решение поставленной задачи. В Exel алгоритм записывается в виде последовательности операторов, включающих значение, ссылки и формулы.

Алгоритм обладает свойствами:

однозначности – исключает произвольное толкование и приводит к одному и тому же результату при одинаковых исходных данных;

массовости – применяется к другим подобным задачам;

результативность – пошаговое выполнение задачи приводит к конечному результату.

Выделяется несколько типов алгоритмических структур:

Линейная структура.

Разветвляющая структура:

с одной ветвью;

с двумя ветвями;

со множеством ветвей.

Циклическая структура.

Принято выделять две циклические структуры с логическим условием до и после тела цикла.

Применительно к электронным таблицам это не совсем точно и справедливо, так как важен и способ организации выхода из цикла, а это:

бесконечный цикл;

вложенные циклические структуры;

цикл с заданным заранее количеством повторений;

-расчетно-динамический цикл (новый, характерный для электронной таблицы), количество повторений которого определяется в ходе пересчета таблицы, а параметры задаются в результате ссылки на ячейку, где содержаться расчетно-переменные данные.

итерационный цикл (количество повторений заранее неизвестно и зависит от осуществления или достижения заданной точности или последовательности приближений к искомому значению, где вычисление последующего члена производится через предыдущий член);

5 Метод половинного деления

Этот метод отличается от выше рассмотренных методов тем, что для него не требуется выполнения условия, что первая и вторая производная сохраняют знак на интервале [a, b]. Метод половинного деления сходится для любых непрерывных функций f(x) в том числе недифференцируемых.

Разделим отрезок [a, b] пополам точкой Если (что практически наиболее вероятно), то возможны два случая: либо f(x) меняет знак на отрезке [a, c] (Рис. 1), либо на отрезке [c, b] (Рис. 2)

Рис. 1

Рис. 2

Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

6 РЕШЕНИЕ ЗАДАЧИ

Дана следующая функция:

F(х)=60*sin(5.5*x*pi/180)-69*cos(2.7*x*pi/180)-exp(x/192)-181/x

где Х изменяется от 0 до 400. Найти точки пересечения функции с точкой А (А=0).

Для нахождения точек пересечения используем метод половинного деления. Для этого от данной функции отнимем А (F(x)-А).

Построим алгоритм (приложение А).

Для того, что бы найти точки пересечения функции с точкой А, построим график (приложение В) по данным приведенным в таблице (приложение Г).

В графе Е2 введем формулу для нахождения значений где происходит смена знака =ЕСЛИ(В2*В3<=0; “смена знака”;” “).

По полученным данным найдем точки пересечения данной функции с точкой А в точках где происходит смена знака.

Например, смена знака происходит при значении Х=15, тогда в ячейку G2 введем значение Х1=15,а в ячейку G3 введем формулу =ЕСЛИ(J2*L2<=0;G2;I2). В ячейку Н2-значение Х2=20, а в ячейку Н3 введем формулу =ЕСЛИ(J2*L2<=0;I2;H2), это значит, что на этом интервале про исходит пересечение функции с координатной осью, то есть с точкой А. Для нахождения среднего значения в ячейку I2 введем формулу =(G2+H2)/2. В ячейки J2, K2, L2 введем формулы заданной в условии функции, где Х, для каждой из заданных ячеек, будет принимать значение Х1, Х2, Хср. соответственно.

Для того, чтобы определить на какой половине происходит смена знака в ячейку М2 введем формулу

=ЕСЛИ(J2*L2<=0;”смена знака на 1-ой половине”;”cмена знака на 2-ой половине”).

В столбце N приведено количество шагов, за которое будит достигнута точность определения значения (х) не ниже 0,001.

Для определения погрешности, в ячейку О2 введем формулу =0-L2. Таким образом из приведенной таблицы видно, что значение Х с точностью до 0,001 определено за 14 шагов.

X1	X2	Xср	F(x1)	F(x2)	F(xcр)		Кол-во шагов	Погреш-ность
15,000	20,000	17,500	-6,129	5,665	1,368	смена знака на 1-ой половине	1	-1,3678
15,000	17,500	16,250	-6,129	1,368	-1,969	смена знака на 2-ой половине	2	1,9692
16,250	17,500	16,875	-1,969	1,368	-0,199	смена знака на 2-ой половине	3	0,1991
16,875	17,500	17,188	-0,199	1,368	0,610	смена знака на 1-ой половине	4	-0,6096
16,875	17,188	17,031	-0,199	0,610	0,212	смена знака на 1-ой половине	5	-0,2116
16,875	17,031	16,953	-0,199	0,212	0,008	смена знака на 1-ой половине	6	-0,0078
16,875	16,953	16,914	-0,199	0,008	-0,095	смена знака на 2-ой половине	7	0,0952
16,914	16,953	16,934	-0,095	0,008	-0,044	смена знака на 2-ой половине	8	0,0436
16,934	16,953	16,943	-0,044	0,008	-0,018	смена знака на 2-ой половине	9	0,0179
16,943	16,953	16,948	-0,018	0,008	-0,005	смена знака на 2-ой половине	10	0,0050
16,948	16,953	16,951	-0,005	0,008	0,001	смена знака на 1-ой половине	11	-0,0014
16,948	16,951	16,949	-0,005	0,001	-0,002	смена знака на 2-ой половине	12	0,0018
16,949	16,951	16,950	-0,002	0,001	0,000	смена знака на 2-ой половине	13	0,0002
16,950	16,951	16,950	0,000	0,001	0,001	смена знака на 1-ой половине	14	-0,0006

G H I J K L M N O

По полученным данным с помощью мастера диаграмм построим график погрешности.

Для определения правильности решения произведем проверку с помощью подбора параметров.

Для этого в ячейку А107 введем формулу заданной функции, а в ячейку В107 введем значение Х при котором происходит смена знака. Далее необходимо поставить курсор в ячейку А107 и из меню сервис выбрать подбор параметра. В появившемся окне ввести необходимые данные, нажать кнопку ОК.

	А	В
105	Подбор параметров
106	F(X)	X
107	0,0000	16,950
108	0,0005	28,806
109	0,0003	54,235
110	0,0000	98,448
111	-0,0002	146,365
112	0,0000	158,039
113	0,0000	185,884
114	0,0001	230,163
115	0,0000	318,118
116	0,0009	361,607

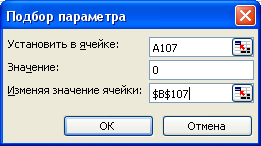
В появившемся окне Результат подбора параметра нужно нажать

кнопку ОК, после чего в ячейках А107 и В107 появится результат поиска.

7 Понятие оптимизационных задач и оптимизационных моделей

Экономико-математические задачи, цель которых состоит в нахождении наилучшего, то есть оптимального с точки зрения одного или нескольких критериев варианта использования имеющихся ресурсов, называются оптимизационными.

Оптимизационные задачи решаются с помощью оптимизационных моделей методами математического программирования.

Математическое программирование – это раздел прикладной математики, который изучает задачи оптимизации и методы их решения с ориентацией на современные средства компьютерной техники.

Структура оптимизационной модели включает целевую функцию, области допустимых решений и системы ограничений, определяющих эту область. Целевая функция в самом общем виде также состоит из трех элементов:

управляемых переменных;

неуправляемых переменных;

формы функции (вида зависимости между ними).

Область допустимых решений – это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами и условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.

Главная задача математического программирования – это нахождение экстремума функций при выполнении указанных ограничений. Если система ограничений несовместима, то область допустимых решений является пустой.

Сущность задач оптимизации: определить значение переменных х_>1>, х_>2>,..., х_>n>, которые обеспечивают экстремум целевой функции Е, с учетом ограничений, наложенных на аргументы этой функции. При этом сложность решения задач зависит:

от вида функциональных зависимостей, то есть от связи функции Е с элементами решения;

от размерности задачи, то есть от количества элементов решения;

от вида и количества ограничений, накладываемых на элементы решения.

8 РЕШЕНИЕ ЗАДАЧИ

Кондитерская фабрика для производства трех видов карамели А, В и С использует три вида сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья на производство 1 кг. Карамели заданы в таблице.

Наименование сырья	Нормы расхода (кг./кг.)
A	B	C
Сахарный песок	0,6	0,5	0,6
Патока	0,4	0,4	0,3
Фруктовое пюре	0,1	0,2	0,2

Запасы сырья на складе соответственно равны V1, V2 и V3 кг. Прибыль от реализации 1 кг. Продукции каждого вида определяется значениями РА, РВ и РС. Найти план производства карамели, обеспечивающий максимальную прибыль.

Запасы сырья (кг.)	Прибыль от реализации (руб./кг.)
V1	V2	V3	Pa	Pb	Pc
800	600	120	1,08	1,12	1,28

Подготовим задачу к решению.

Пусть х_>1> – карамель вида А (кг.)

х_>2> – карамель вида В (кг.)

х_>3> – карамель вида С (кг.).

Тогда система ограничений и целевая функция запишутся следующим образом:

Ра*Х1+Рв*Х2+Рс*Х3 =>mах (целевая функция);

х1*0,6+х2*0,5+х3*0,6<=800

х1*0,4+х2*0,4+х3*0,3<=600 ограничения на запасы сырья (сахарный

х1*0.1+х2*0,2+х3*0,2<=120 песок, патока, фруктовое пюре)

х1>=0; x2>=0; x3>=0;

x1, x2, x3- целые числа.

Для решения задачи в Excel запишем ее в виде, представленном на таблице 1.

Таблица 1 – Таблица для решения задачи

	Кг.	ограничение
х1	0	800	>=	0
х2	0	600	>=	0
х3	0	120	>=	0
Mах прибыль:	0

В соответствии с условием прибыль должна быть максимальной, поэтому в таблице 1 добавлена строка «Mах прибыль». В ней буду суммировать прибыль от реализации продукции.

Вызываю Поиск решения из меню Сервис.

Определяю целевую ячейку – $D$8, устанавливаю переключатель в максимальное значение. Ввожу диапазон изменяемых ячеек ($B$11:$В$13) и вношу ограничения. Прежде всего, количество продукта не может быть отрицательным ($B$11:$В$13>=0), далее добавляю ограничения на запасы сырья, которое должно быть не более нормативного (800>=G$5; 600>=G$6; 120>=G$7). Нажимаю кнопку Выполнить.

В появившемся окне Результаты поиска решения нажимаю кнопку ОК и получаю решение задачи (приложение Д).Из полученных данных видно, что максимальная прибыль при производстве карамели составила 1296 рублей, причем такая прибыль будет получена при производстве 1200кг. Карамели вида А.

Для проверки правильности решения введем дополнительные ограничения.

В первом варианте я ввела ограничение на карамель вида В и получила результат приведенный в таблице 1.

Таблица 1

Вариант 1				Запасы сырья (кг.)		Ограничение
Х1	1170			800	>=	709,5
Х2	15			600	>=	474
Х3	0			120	>=	120
Целевая функция	1280,4	Дополнительное ограничение	Х2>=15

Из таблицы видно, что прибыль по сравнению с данными полученными в приложении Д уменьшилась на 15,6 рублей, при этом уменьшилось и производство карамели вида А на 30кг.

Во втором варианте я ввела ограничение на карамель вида С и получила следующий результат

Вариант 2		Запасы сырья (кг.)		Ограничение
Х1	1180	800	>=	714
Х2	0	600	>=	475
Х3	10	120	>=	120
Целевая функция	1287,2	Дополнительное ограничение	Х3>=10

Из полученных данных видно, что прибыль, так же как и в первом варианте, уменьшилась относительно данных из приложения Д на 8,8 рубля, а производство карамели вида А уменьшилось на 20кг.

По полученным данным можно сделать вывод, что исходное решение задачи было верным.

ЗАКЛЮЧЕНИЕ

В данной курсовой работе были решены оптимизационные задачи с использованием программных средств Microsoft Excel.

В процессе решения первой задачи были построены: график функции F(x) с учетом параметра А=0 в заданном диапазоне значений переменной Х, которые изменяются в диапазоне от 0 до 400. Были найдены интервалы значений переменной Х в пределах, которых функция принимает значение параметра А. При использовании метода половинного деления были найдены значения переменной Х, при которых функция принимает значение параметра А, в соответствии с заданной точностью, равной 0,001. Проверка правильности вычислений была осуществлена с помощью «Подбора параметра».

Решение второй задачи осуществлялось с помощью «Поиска решений» средствами Microsoft Excel. Была составлена целевая функция и ограничения (соответствующие условию задачи). В результате был выбран оптимальный вариант решения задачи. Для проверки этого варианта были внесены дополнительные ограничения, которые показали, что исходно оптимальный вариант решения был верен.

ПРИЛОЖЕНИЕ А

Начало

Описание F(х), А, ∆

Ввод а, b

с=(a+b)/2

F(a), F(b), F(c)

нет да

(F(a)-A)+(F(c)-A)<=0

a: = c b: = c

нет да

(b-a)<=∆

Выво с,F(c), F(c)-A

Конец

ПРИЛОЖЕНИЕ Б

ПРИЛОЖЕНИЕ В

ПРИЛОЖЕНИЕ Г

А В С D E

X	F(x)	A	F(x)-A	Смена знака
5	-76,6150	0	-76,6150
10	-31,4838	0	-31,4838
15	-6,1292	0	-6,1292	смена знака
20	5,6646	0	5,6646
25	5,7512	0	5,7512	смена знака
30	-2,4673	0	-2,4673
35	-13,9441	0	-13,9441
40	-23,0017	0	-23,0017
45	-24,6667	0	-24,6667
50	-15,8988	0	-15,8988	смена знака
55	3,6061	0	3,6061
60	31,2394	0	31,2394
65	61,9826	0	61,9826
70	89,4820	0	89,4820
75	107,4577	0	107,4577
80	111,1312	0	111,1312
85	98,3486	0	98,3486
90	70,1426	0	70,1426
95	30,6047	0	30,6047	смена знака
100	-13,9123	0	-13,9123
105	-56,0851	0	-56,0851
110	-89,1227	0	-89,1227
115	-108,1489	0	-108,1489
120	-111,1603	0	-111,1603
125	-99,3512	0	-99,3512
130	-76,7403	0	-76,7403
135	-49,1871	0	-49,1871
140	-23,0264	0	-23,0264
145	-3,6307	0	-3,6307	смена знака
150	5,7743	0	5,7743
155	4,7747	0	4,7747	смена знака
160	-4,2332	0	-4,2332
165	-16,7039	0	-16,7039
170	-27,1093	0	-27,1093
175	-30,3377	0	-30,3377
180	-23,0020	0	-23,0020
185	-4,3520	0	-4,3520	смена знака
190	23,4221	0	23,4221
195	55,5727	0	55,5727
200	85,7823	0	85,7823
205	107,5385	0	107,5385
210	115,5876	0	115,5876
215	107,1397	0	107,1397
220	82,5521	0	82,5521
225	45,3337	0	45,3337
230	1,4645	0	1,4645	смена знака
	235	-41,8225	0	-41,8225
	240	-77,5282	0	-77,5282
	245	-100,3165	0	-100,3165
	250	-107,5698	0	-107,5698
	255	-99,8416	0	-99,8416
	260	-80,6115	0	-80,6115
	265	-55,4037	0	-55,4037
	270	-30,4751	0	-30,4751
	275	-11,3711	0	-11,3711
	280	-1,6789	0	-1,6789
	285	-2,2580	0	-2,2580
	290	-11,1210	0	-11,1210
	295	-23,9866	0	-23,9866
	300	-35,3741	0	-35,3741
	305	-39,9858	0	-39,9858
	310	-34,0560	0	-34,0560
	315	-16,3539	0	-16,3539	смена знака
	320	11,3948	0	11,3948
	325	44,7702	0	44,7702
	330	77,5536	0	77,5536
	335	103,0577	0	103,0577
	340	115,5964	0	115,5964
	345	111,7635	0	111,7635
	350	91,2325	0	91,2325
	355	56,8943	0	56,8943
	360	14,2986	0	14,2986	смена знака
	365	-29,4800	0	-29,4800
	370	-67,3017	0	-67,3017
	375	-93,4252	0	-93,4252
	380	-104,6518	0	-104,6518
	385	-100,9012	0	-100,9012
	390	-85,0963	0	-85,0963
	395	-62,3901	0	-62,3901
	400	-38,9164	0	-38,9164	смена знака

ПРИЛОЖЕНИЕ Д

A	B	C	D	E	F	G
Наименование сырья	Нормы расхода (кг./кг.)	Запасы сырья (кг.)		Ограничение
A	B	C
Сахарный песок	0,6	0,5	0,6	800	>=	720
Патока	0,4	0,4	0,3	600	>=	480
Фруктовое пюре	0,1	0,2	0,2	120	>=	120
Прибыль от реализации (руб./кг.)	1,08	1,12	1,28
		Целевая функция	1296
x1	1200			А=х1
x2	0			В=х2
x3	0			С=х3

Литература

Банди Б. Основы линейного программирования. – М.: Радио и связь, 1989.

Карпов Б. Microsoft Excel 2000. Справочник.- Питер, 2002.

Семенищенков А. Microsoft Excel. Параметры и методы практического программирования. – Брянск, 1998.

Рычков В. Microsoft Excel 2000. – Питер, 2000.