Применение методов линейного программирования для оптимизации стоимости перевозок
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Реферат
по дисциплине: Методы и модели в экономике и менеджменте.
на тему: «Применение методов линейного программирования для оптимизации стоимости перевозок»
Воронеж 2010
Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
В общей постановке
транспортная задача состоит в отыскании
оптимального плана перевозок некоторого
однородного груза с
 баз
баз
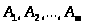
 потребителям
потребителям
 .
.
Различают два типа транспортных задач: но критерию стоимости (план перевозок оптимален, если достигнут минимум затрат на его реализацию) и по критерию времени (план оптимален, если на его реализацию затрачивается минимум времени).
О
(3. )
бозначим количество груза, имеющегося на каждой из баз (запасы),
соответственно
баз (запасы),
соответственно
 ,а
общее количество имеющегося в наличии
груза–
,а
общее количество имеющегося в наличии
груза– :
:
 ;
;
з
(3. )
аказы каждого из потребителей (потребности) обозначим соответственно ,
а общее количество потребностей –
,
а общее количество потребностей –
 :
:
 ,
,
Т
(3. )
огда при условии

м
(3. )
ы имеем закрытую модель, а при условии

– открытую модель транспортной задачи.
Очевидно, в случае закрытой
модели весь имеющийся в наличии груз
развозится полностью, и все потребности
заказчиков полностью удовлетворены; в
случае же открытой модели либо все
заказчики удовлетворены и при этом на
некоторых базах остаются излишки груза
 ,
либо весь груз оказывается израсходованным,
хотя потребности полностью не удовлетворены
,
либо весь груз оказывается израсходованным,
хотя потребности полностью не удовлетворены
 .
.
Так же существуют одноэтапные модели задач, где перевозка осуществляется напрямую от, например, базы или завода изготовителя к потребителю, и двухэтапные, где между ними имеется “перевалочный пункт”, например – склад.
План перевозок с указанием запасов и потребностей удобно записывать в виде следующей таблицы, называемой таблицей перевозок (Таблица 3. ):
Таблица 3. - План перевозок с указанием запасов и потребностей
|
Пункты Отправления |
Пункты назначения |
Запасы |
|||
|
|
|
… |
|
||
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
… |
… |
… |
… |
… |
… |
|
|
|
|
… |
|
|
|
Потребности |
|
|
… |
|
или
|
Условие
 или
или
 означает, с какой задачей мы имеем дело,
с закрытой моделью или открытой моделью
транспортной задачи. Переменное
означает, с какой задачей мы имеем дело,
с закрытой моделью или открытой моделью
транспортной задачи. Переменное
 означает количество груза, перевозимого
с базы
означает количество груза, перевозимого
с базы
 потребителю
потребителю
 :
совокупность этих величин образует
матрицу (матрицу перевозок).
:
совокупность этих величин образует
матрицу (матрицу перевозок).
Очевидно, переменные
 должны удовлетворять условиям:
должны удовлетворять условиям:

(3. )


Система (3. ) содержит
 уравнений с
уравнений с
 неизвестными. Её особенность состоит
в том, что коэффициенты при неизвестных
всюду равны единице. Кроме того, все
уравнения системы (3. ) могут быть разделены
на две группы: первая группа из т
первых уравнений (“горизонтальные”
уравнения) и вторая группа из п
остальных уравнений (“вертикальные”
уравнения). В каждом из горизонтальных
уравнений содержатся неизвестные с
одним и тем же первым индексом (они
образуют одну строку матрицы перевозок),
в каждом из вертикальных уравнений
содержатся неизвестные с одним и тем
же вторым индексом (они образуют один
столбец матрицы перевозок). Таким
образом, каждая неизвестная встречается
в системе (3. ) дважды: в одном и только
одном горизонтальном и в одном и только
одном вертикальном уравнениях.
неизвестными. Её особенность состоит
в том, что коэффициенты при неизвестных
всюду равны единице. Кроме того, все
уравнения системы (3. ) могут быть разделены
на две группы: первая группа из т
первых уравнений (“горизонтальные”
уравнения) и вторая группа из п
остальных уравнений (“вертикальные”
уравнения). В каждом из горизонтальных
уравнений содержатся неизвестные с
одним и тем же первым индексом (они
образуют одну строку матрицы перевозок),
в каждом из вертикальных уравнений
содержатся неизвестные с одним и тем
же вторым индексом (они образуют один
столбец матрицы перевозок). Таким
образом, каждая неизвестная встречается
в системе (3. ) дважды: в одном и только
одном горизонтальном и в одном и только
одном вертикальном уравнениях.
Такая структура системы
(3. ) позволяет легко установить ее ранг.
Действительно, покажем, что совокупность
неизвестных, образующих первую строку
и первый столбец матрицы перевозок,
можно принять в качестве базиса. При
таком выборе базиса, по крайней мере,
один из двух их индексов равен единице,
а, следовательно, свободные неизвестные
определяются условием
 ,
,
 .Перепишем
систему (3. ) в виде
.Перепишем
систему (3. ) в виде

(3. )

где символы
 и
и
 означают
суммирование по соответствующему
индексу. Так, например,
означают
суммирование по соответствующему
индексу. Так, например,

При
этом легко заметить, что под символами
такого суммирования объединяются только
свободные неизвестные (здесь
 ,
,
 ).
).
В рассматриваемой нами
системе только два уравнения, а именно
первое горизонтальное и первое
вертикальное, содержат более одного
неизвестного из числа выбранных нами
для построения базиса. Исключив из
первого горизонтального уравнения
базисные неизвестные
 с помощью вертикальных уравнений, мы
получаем уравнение
с помощью вертикальных уравнений, мы
получаем уравнение

или короче

(3. )
где символ
 означает сумму всех свободных неизвестных.
Аналогично, исключив из первого
вертикального уравнения базисные
неизвестные
означает сумму всех свободных неизвестных.
Аналогично, исключив из первого
вертикального уравнения базисные
неизвестные
 с помощью горизонтальных уравнений, мы
получаем уравнение
с помощью горизонтальных уравнений, мы
получаем уравнение

(3. )
Так как для закрытой
модели транспортной задачи
 ,
то полученные нами уравнения (3. ) и (3. )
одинаковы и, исключив из одного из них
неизвестное
,
то полученные нами уравнения (3. ) и (3. )
одинаковы и, исключив из одного из них
неизвестное
 ,
мы получим уравнение-тождество 0=0,
которое из системы вычеркивается.
,
мы получим уравнение-тождество 0=0,
которое из системы вычеркивается.
Итак, преобразование системы (3. ) свелось к замене двух уравнений (первого горизонтального и первого вертикального) уравнением (3. ). Остальные уравнения остаются неизменными. Система приняла вид


(3. )
В системе (3. ) выделен
указанный выше базис: базисные неизвестные
из первых т
уравнений образуют первый столбец
матрицы перевозок, а базисные неизвестные
остальных уравнений образуют первую
строку матрицы перевозок без первого
неизвестного
 [она входит в первое уравнение системы
(3. )]. В системе (3. ) имеется
[она входит в первое уравнение системы
(3. )]. В системе (3. ) имеется
 уравнений, выделенный базис содержит
уравнений, выделенный базис содержит
 неизвестных, а, следовательно, и ранг
системы (3. )
неизвестных, а, следовательно, и ранг
системы (3. )
 .
.
Для решения транспортной
задачи необходимо кроме запасов и
потребностей знать также и тарифы
 ,
т. е. стоимость перевозки единицы груза
с базы
,
т. е. стоимость перевозки единицы груза
с базы
 потребителю
потребителю
 .
.
Совокупность тарифов
 также образует матрицу, которую можно
объединить с матрицей перевозок и
данными о запасах и потребностях в одну
таблицу 3.:
также образует матрицу, которую можно
объединить с матрицей перевозок и
данными о запасах и потребностях в одну
таблицу 3.:
Таблица 3. - Совокупность тарифов данные о запасах и потребностях
|
Пункты Отправления |
Пункты назначения |
Запасы |
||||||
|
|
|
… |
|
|||||
|
|
|
|
… |
|
|
|||
|
|
|
|
||||||
|
|
|
|
… |
|
|
|||
|
|
|
|
||||||
|
… |
… |
… |
… |
… |
… |
|||
|
|
|
|
… |
|
|
|||
|
|
|
|
||||||
|
Потребности |
|
|
… |
|
или
|
Сумма всех затрат, т. е.
стоимость реализации данного плана
перевозок, является линейной функцией
переменных
 :
:

(3. )
Требуется в области допустимых решений системы уравнений (3. ) и (3.) найти решение, минимизирующее линейную функцию (3. ).
Таким образом, мы видим,
что транспортная задача является задачей
линейного программирования. Для ее
решения применяют также симплекс-метод,
но в силу специфики задачи здесь можно
обойтись без симплекс-таблиц. Решение
можно получить путем некоторых
преобразований таблицы перевозок. Эти
преобразования соответствуют переходу
от одного плана перевозок к другому.
Но, как и в общем случае, оптимальное
решение ищется среди базисных решений.
Следовательно, мы будем иметь дело
только с базисными (или опорными) планами.
Так как в данном случае ранг системы
ограничений-уравнений равен
 то среди всех
то среди всех
 неизвестных
неизвестных
 выделяется
выделяется
 базисных неизвестных, а остальные
базисных неизвестных, а остальные
 ·
· неизвестных являются свободными. В
базисном решении свободные неизвестные
равны нулю. Обычно эти нули в таблицу
не вписывают, оставляя соответствующие
клетки пустыми. Таким образом, в таблице
перевозок, представляющей опорный план,
мы имеем
неизвестных являются свободными. В
базисном решении свободные неизвестные
равны нулю. Обычно эти нули в таблицу
не вписывают, оставляя соответствующие
клетки пустыми. Таким образом, в таблице
перевозок, представляющей опорный план,
мы имеем
 заполненных и
заполненных и
 ·
· пустых клеток.
пустых клеток.
На предприятии ОАО «Электросигнал» имеется 4 транзитных склада А>i>, на которых хранятся сборочные узлы и 5 цехов B>j>, занимающихся сборкой готовой продукции. Ниже, в таблице 3., приведены данные по количеству сборочных узлов на каждом складе, запросы цехов и стоимость перевозки одного агрегата из А>i> в B>j>. Необходимо составить такой план перевозок, при котором запросы цехов будут удовлетворены при минимальной суммарной стоимости перевозок.
Таблица 3. – Исходные данные по количеству сборочных узлов и стоимость перевозки
|
Склад |
B>1> (b>1>=40) |
B>2> (b>2>=50) |
B>3> (b>3>=15) |
B>4> (b>4>=75) |
B>5> (b>5>=40) |
|
А>1 >(а>1>=50) |
1,0 |
2,0 |
3,0 |
2,5 |
3,5 |
|
А>2>(а>2>=20) |
0,4 |
3,0 |
1,0 |
2,0 |
3,0 |
|
А>3>(а>3>=75) |
0,7 |
1,0 |
1,0 |
0,8 |
1,5 |
|
А>4>(а>4>=80) |
1,2 |
2,0 |
2,0 |
1,5 |
2,5 |
В данном случае Σa>i>=225 >Σb>j>=220 => имеем дело с открытой моделью транспортной задачи. Сведем ее к закрытой введением фиктивного цеха B>6> с потребностью b>5>=225-220=5 и стоимостью перевозок с>i>>6>=0.Имеем таблицу 3. :
Таблица 3. -
|
Склад |
B>1 > (b>1>=40) |
B>2 > (b>2>=50) |
B>3 > (b>3>=15) |
B>4 > (b>4>=75) |
B>5> (b>5>=40) |
B>6> (b>6>=5) |
|
А>1 >(а>1>=50) |
1,0 |
2,0 |
3,0 |
2,5 |
3,5 |
0 |
|
А>2>(а>2>=20) |
0,4 |
3,0 |
1,0 |
2,0 |
3,0 |
0 |
|
А>3>(а>3>=75) |
0,7 |
1,0 |
1,0 |
0,8 |
1,5 |
0 |
|
А>4>(а>4>=80) |
1,2 |
2,0 |
2,0 |
1,5 |
2,5 |
0 |
Математическая модель: обозначим x>ij> – количество товара, перевозимого из А>i> в B>j>. Тогда
x >11
>x>12
>x>13
>x>14
>x>15>
x>16>
>11
>x>12
>x>13
>x>14
>x>15>
x>16>
x>21 >x>22 >x>23 >x>24 >x>25> x>26>
X = x>31 >x>32 >x>33 >x>34 >x>35> x>36> - матрица перевозок.
x>41 >x>42 >x>43 >x>44 >x>45> x>46>
min(x>11>+2x>12>+3x>13>+2,5x>14>+3,5x>15>+0,4x>21>+3x>22>+x>23>+2x>24>+3x>25>+0,7x>31>+x>32>+x>33>+0,8x>34>+1,5x>35>++1,2x>41>+2x>42>+2x>43>+1,5x>44>+2,5x>45>) (3. )> >
x>11>+x>12>+x>13>+x>14>+x>15>+x>16>=50
x >21>+x>22>+x>23>+x>24>+x>25>+x>26>=20
>21>+x>22>+x>23>+x>24>+x>25>+x>26>=20
x>31>+x>32>+x>33>+x>34>+x>35>+x>36>=75
x>41>+x>42>+x>43>+x>44>+x>45>+x>46>=80
(3. )
x>11>+x>21>+x>31>+x>41>=40x>12>+x>22>+x>32>+x>42>=50
x>13>+x>23>+x>33>+x>43>=15
x>14>+x>24>+x>34>+x>44>=75
x>15>+x>25>+x>35>+x>45>=40
x>16>+x>26>+x>36>+x>46>=5
x>ij>≥0 (i=1,2,3,4 ; j=1,2,3,4,5,6 ) (3. )
Двойственная ЗЛП:
max(50u>1>+20u>2>+75u>3>+80u>4>+40v>1>+50v>2>+15v>3>+75v>4>+40v>5>+5v>6>) (3. )> >
u>2>+v>1>≤0,4
u>2>+v>2>≤3
u>2>+v>3>≤1
u>2>+v>4>≤2
u>2>+v>5>≤3
u>2>+v>6>≤0
u>3>+v>1>≤0,7
u>3>+v>2>≤1
u>3>+v>3>≤1
u>3>+v>4>≤0,8
u>3>+v>5>≤1,5
u>3>+v>6>≤0
u>4>+v>1>≤1,2
u>4>+v>2>≤2
u>4>+v>3>≤2
u>4>+v>4>≤1,5
u>4>+v>5>≤2,5
u>4>+v>6>≤0
u >1>+v>1>≤1
>1>+v>1>≤1
u>1>+v>2>≤2
u>1>+v>3>≤3 (3. )
u>1>+v>4>≤2,5
u>1>+v>5>≤3,5
u>1>+v>6>≤0
u>i>,v>j> – произвольные (i=1,2,3,4 ; j=1,2,3,4,5,6 )
Будем искать первоначальный план по методу наименьшей стоимости:
1) x>21>=20> >и 2-ую строку исключаем;
2) x>31>=20> >и 1-ый столбец исключаем;
3) x>34>=55> >и 3-ю строку исключаем;
4) x>44>=20> >и 4-ый столбец исключаем;
5) x>12>=50 и 1-ю строку и 2-ой столбец исключаем и x>32>=0;
6) x>43>=150 и 3-ий столбец исключаем;
7) x>45>=40 и 5-ый столбец исключаем и x>46>=5.
Составим таблицу 3. . Здесь и далее в нижнем правом углу записываем значение перевозки.
Таблица 3. – Проведение итераций
|
Склад |
B>1 > (b>1>=40) |
B>2 > (b>2>=50) |
B>3 > (b>3>=15) |
B>4 > (b>4>=75) |
B>5> (b>5>=40) |
B>6> (b>6>=5) |
|
А>1 >(а>1>=50) |
1,0 |
50 2,0 |
3,0 |
2,5 |
3,5 |
0 |
|
А>2>(а>2>=20) |
20 |
3,0 |
1,0 |
2,0 |
3,0 |
0 |
|
А>3>(а>3>=75) |
20 |
0 1,0 |
1,0 |
55 0,8 |
1,5 |
0 |
|
15 5 А>4>(а>4>=80) |
1,2 |
2,0 |
2,0 |
20 1,5 |
40 2,5 |
0 |
Стоимость 1-ого плана:
D>1>=2•50+0,4•20+0,7•20+0,8•55+2•15+1,5•20+2,5•40=326.
Будем улучшать этот план методом потенциалов: u>i>- потенциал А>i> ,v>j>- потенциал B>j>. Тогда u>1>+v>2>=2,u>2>+v>1>=0,4, u>3>+v>1>=0,7, u>3>+v>2>=1, u>3>+v>4>=0,8, u>4>+v>3>=2, u>4>+v>4>=1,5, u>4>+v>5>=2,5 ,u>4>+v>6>=0.Положим u>1>=0,тогда v>2>=2,u>3>=-1,v>1>=1,7,v>4>=1,8, u>2>=-1,3,u>4>=-0,3, v>3>=2,3,v>5>=2,8,v>6>=0,3.Составим таблицу 3. :
Таблица 3. - Проведение итераций
|
Склад |
B>1 > (b>1>=40) v>1>=1,7 |
B>2 > (b>2>=50) v>2>=2 |
B>3 > (b>3>=15) v>3>=2,3 |
B>4 > (b>4>=75) v>4>=1,8 |
B>5> (b>5>=40) v>5>=2,8 |
B>6> (b>6>=5) v>6>=0,3 |
|
0,7  А>1
>(а>1>=50) А>1
>(а>1>=50)
U>1>=0 |
0 
 1,0 1,0
|
50 - 0,7 
 2,0 2,0
|
- 0,7 3,0 |
- 0,7 2,5 |
0,3 3,5 |
0 |
|
0 А>2>(а>2>=20)U>2>=-1,3 |
20 - 2,3 0,4 |
0 3,0 |
- 1,5 1,0 |
- 1,5 2,0 |
- 1 3,0 |
0 |
|
0 А>3>(а>3>=75)U>3>=-1 |
0  0,7 0,7
20  |
0 0,3  1,0 1,0
|
0 1,0 |
55 0,3 0,8 |
- 0,7 1,5 |
0 |
|
0,2 А>4>(а>4>=80)U>4>=-0,3 |
- 0,3 1,2 |
0 2,0 |
15 0 2,0 |
20 0 1,5 |
40 0 2,5 |
5 0 |
В верхнем левом углу здесь и далее записываем значение u>i>+v>j>-c>ij>. Имеем: u>1>+v>1>--c>11 >=0,7>0, u>1>+v>6>-c>16 >=0,3>0, u>3>+v>3>-c>33 >=0,3>0, u>3>+v>5>-c>35 >=0,3>0,
u>4>+v>1>-c>41 >=0,2>0. => По критерию оптимальности, первый план не оптимален. Далее max(0,7;0,3;0,3;0,3;0,2)=0,7. => Поместим перевозку в клетку А>1>В>1>,> >сместив 20=min(20,50) по циклу, указанному в таблице штрихом. Получим новую таблицу. Найдем потенциалы: u>1>+v>1>=1,u>1>+v>2>=2,u>2>+v>1>=0,4,u>3>+v>2>=1, u>3>+v>4>=0,8, u>4>+v>3>=2, u>4>+v>4>=1,5, u>4>+v>5>=2,5 , u>4>+v>6>=0. Положим u>1>=0,тогда v>1>=1,u>2>=-0,6,v>2>=2,v>4>=1,8, u>3>=-1, u>4>=-0,3,v>3>=2,3,v>5>=2,8,v>6>=0,3. Составим таблицу 3. :
Таблица 3. - Проведение итераций
|
Склад |
B>1 > (b>1>=40) v>1>=1 |
B>2 > (b>2>=50) v>2>=2 |
B>3 > (b>3>=15) v>3>=2,3 |
B>4 > (b>4>=75) v>4>=1,8 |
B>5> (b>5>=40) v>5>=2,8 |
B>6> (b>6>=5) v>6>=0,3 |
|
0 А>1 >(а>1>=50)U>1>=0 |
0 

 1,0 1,0
20 |
30 - 0,7 
 2,0 2,0
|
- 0,7 3,0 |
- 0,7 2,5 |
0,3 3,5 |
0 |
|
0 А>2>(а>2>=20)U>2>=-0,6 |
20 - 1,6  0,4 0,4
|
0,7 3,0 |
- 0,8 
 1,0 1,0
|
- 0,8 2,0 |
- 0,3 3,0 |
0 |
|
-0,7 А>3>(а>3>=75)U>3>=-1 |
0 0,7 |
20 0,3 
 1,0 1,0
|
0 1,0 |
55 0,3 
 0,8 0,8
|
- 0,7 1,5 |
0 |
|
-0,5 А>4>(а>4>=80)U>4>=-0,3 |
- 0,3 1,2 |
0 2,0 |
15 0 
 2,0 2,0
|
20 0  1,5 1,5
|
40 0 2,5 |
5 0 |
Стоимость 2-ого плана:
D>2>=1•20+2•30+0,4•20+1•20+0,8•55+2•15+1,5•20+2,5•40=312.
Имеем:u>1>+v>6>-c>16 >=0,3>0, u>2>+v>3>-c>23 >=0,7>0, u>3>+v>3>-c>33 >=0,3>0, u>3>+v>5>-c>35 >=0,3>0. => По критерию оптимальности, второй план не оптимален. Далее max(0,3;0,7;0,3;0,3)=0,7 => Поместим перевозку в клетку А>2>В>3>,> >сместив 15=min(20,30,55,15) по циклу, указанному в таблице штрихом. Получим новую таблицу. Найдем потенциалы: u>1>+v>1>=1,u>1>+v>2>=2,u>2>+v>1>=0,4,u>3>+v>2>=1, u>3>+v>4>=0,8, u>2>+v>3>=1, u>4>+v>4>=1,5, u>4>+v>5>=2,5 , u>4>+v>6>=0. Положим u>1>=0,тогда v>1>=1,u>2>=-0,6,v>2>=2,v>4>=1,8, u>3>=-1, u>4>=-0,3,v>3>=1,6, v>5>=2,8, v>6>=0,3. Составим таблицу 3.:
Таблица 3. - Проведение итераций
|
Склад |
B>1 > (b>1>=40) v>1>=1 |
B>2 > (b>2>=50) v>2>=2 |
B>3 > (b>3>=15) v>3>=1,6 |
B>4 > (b>4>=75) v>4>=1,8 |
B>5> (b>5>=40) v>5>=2,8 |
B>6> (b>6>=5) v>6>=0,3 |
|
0 А>1 >(а>1>=50)U>1>=0 |
0 1,0
35 |
15 -1,4 2,0 |
- 0,7 3,0 |
- 0,7 2,5 |
0,3 3,5 |
0 |
|
0 А>2>(а>2>=20)U>2>=-0,6 |
5 - 1,6 0,4 |
0 3,0 |
15 - 0,8 1,0 |
- 0,8 2,0 |
- 0,3 3,0 |
0 |
|
-0,7 А>3>(а>3>=75)U>3>=-1 |
0 0,7 |
35 -0,4 1,0 |
0 1,0 |
40 0,3 

 0,8 0,8
|
- 0,7 
 1,5 1,5
|
0 |
|
-0,5 А>4>(а>4>=80)U>4>=-0,3 |
- 0,3 1,2 |
-0,7 2,0 |
0 2,0 |
35 0 
 1,5 1,5
|
40 0  2,5 2,5
|
5 0 |
Стоимость 3-его плана:
D>3>=1•35+2•15+0,4•5+1•15+0,8•40+1•35+1,5•35+2,5•40=301,5.
Имеем:u>1>+v>6>-c>16 >=0,3>0,u>3>+v>5>-c>35 >=0,3>0. => По критерию оптимальности, третий план не оптимален. Далее max(0,3;0,3)=0,3. => Поместим перевозку в клетку А>3>В>5>,> >сместив 40=min(40,40) по циклу, указанному в таблице штрихом. Получим новую таблицу. Чтобы 4-ый план был невырожденным, оставим в клетке А>4>В>5> нулевую перевозку. Найдем потенциалы: u>1>+v>1>=1,u>1>+v>2>=2,u>2>+v>1>=0,4,u>3>+v>2>=1, u>4>+v>5>=2,5, u>2>+v>3>=1, u>4>+v>4>=1,5, u>3>+v>5>=1,5 , u>4>+v>6>=0. Положим u>1>=0,тогда v>1>=1,u>2>=-0,6,v>2>=2,v>4>=1,5, u>3>=-1,u>4>=0, v>3>=1,6, v>5>=2,5, v>6>=0. Составим таблицу 3. :
Таблица 3. - Проведение итераций
|
Склад |
B>1 > (b>1>=40) v>1>=1 |
B>2 > (b>2>=50) v>2>=2 |
B>3 > (b>3>=15) v>3>=1,6 |
B>4 > (b>4>=75) v>4>=1,5 |
B>5> (b>5>=40) v>5>=2,5 |
B>6> (b>6>=5) v>6>=0 |
|
0 А>1 >(а>1>=50)U>1>=0 |
0 1,0
35 |
15 - 1,4 2,0 |
- 1 3,0 |
- 1 2,5 |
0 3,5 |
0 |
|
0 А>2>(а>2>=20)U>2>=-0,6 |
5 - 1,6 0,4 |
0 3,0 |
15 - 1,1 1,0 |
- 1,1 2,0 |
- 0,6 3,0 |
0 |
|
-0,7 А>3>(а>3>=75)U>3>=-1 |
0 0,7 |
35 -0,4 1,0 |
-0,3 1,0 |
0 0,8 |
40 - 1 1,5 |
0 |
|
-0,2 А>4>(а>4>=80)U>4>=0 |
0 1,2 |
-0,4 2,0 |
0 2,0 |
75 0 1,5 |
0 0 2,5 |
5 0 |
Стоимость 4-ого плана:
D>4>=1•35+2•15+0,4•5+1•15+1•35+1,5•40+1,5•75=289,5.
Для всех клеток последней таблицы выполнены условия оптимальности:
1) u>i>+v>j>-с>ij>=0 для клеток, занятых перевозками;
2) u>i>+v>j>-с>ij>> >≤0 для свободных клеток.
Несодержательные ответы:
Прямой ЗЛП:
 35
15 0 0 0 0
35
15 0 0 0 0
5 0 15 0 0 0
X = 0 35 0 0 40 0
0 0 0 75 0 5
min=289,5.
Двойственной ЗЛП:
U>1>=0 ; U>2>=-0,6 ; U>3>=-1 ; U>4>=0 ; V>1>=1 ; V>2>=2 ; V>3>=1,6 ; V>4>=1,5 ; V>5>=2,5 ; V>6>=0.
max=289,5.
Так как min=max, то по критерию оптимальности найдены оптимальные решения прямой и двойственной ЗЛП. Содержательный ответ: Оптимально перевозить так:
Из А>1 >в> >B>1 >– 35 сборочных агрегатов;
Из А>1 >в> >B>2 >– 15 сборочных агрегатов;
Из А>2 >в> >B>1 >– 5 сборочных агрегатов;
Из А>2 >в> >B>3 >– 15 сборочных агрегатов;
Из А>3 >в> >B>2 >– 35 сборочных агрегатов;
Из А>3 >в> >B>5 >– 40 сборочных агрегатов;
Из А>4 >в> >B>4 >– 75 сборочных агрегатов.
При этом стоимость минимальна и составит D>min>=289,5. 5 сборочных агрегатов необходимо оставить на складе А>4> для их последующей перевозки в другие Цеха.
Список использованной литературы
1. Е.Г. Гольштейн, Д.Б. Юдин «Задачи линейного программирования транспортного типа», Москва, 2007.
2. И.Л. Акулич, В.Ф. Стрельчонок «Математические методы и компьютерные технологии решения оптимизационных задач», Рига, 2006.
3. Астафуров В.Г., Колодникова Н. - Компьютерное учебное пособие, раздел “Анализ на чувствительность с помощью двойственной задачи”, Томск-2004.
4. Алесинская Т.В. - Задачи по исследованию операций с решениями. Москва, 2008.
5. Смородинский С.С., Батин Н.В. - Оптимизация решений на основе методов и моделей математического программирования: Учебное пособие. Воронеж, 2009




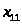

























 Цеха
Цеха Цеха
Цеха Цеха
Цеха 0,4
0,4