Понятие и классификация систем массового обслуживания
Содержание
Введение 3
1 Марковские цепи с конечным числом состояний и дискретным временем 4
2 Марковские цепи с конечным числом состояний и непрерывным временем 7
3 Процессы рождения и гибели 10
4 Основные понятия и классификация систем массового обслуживания 14
5 Основные типы открытых систем массового обслуживания 20
5.1 Одноканальная система массового обслуживания с отказами 21
5.2 Многоканальная система массового обслуживания с отказами 22
5.3 Одноканальная система массового обслуживания с ограниченной длиной очереди 24
5.4 Одноканальная система массового обслуживания с неограниченной очередью 26
5.5 Многоканальная система массового обслуживания с ограниченной очередью 28
5.6 Многоканальная система массового обслуживания с неограниченной очередью 31
5.7 Многоканальная система массового обслуживания с ограниченной очередью и ограниченным временем ожидания в очереди 33
6 Метод Монте-Карло 36
6.1 Основная идея метода 37
6.2 Разыгрывание непрерывной случайной величины 37
6.3 Случайная величина с экспоненциальным распределением 40
7 Исследование системы массового обслуживания 41
7.1 Проверка гипотезы о показательном распределении 42
7.2 Расчет основных показателей системы массового обслуживания 49
7.3 Выводы о работе исследуемой СМО 56
8 Исследование видоизмененной СМО 57
Заключение 60
Список использованных источников 61
Введение
Темой моей дипломной работы является исследование системы массового обслуживания. В своем изначальном состоянии рассматриваемая мной СМО представляет собой один из классических случаев, а конкретно M/M/2/5 по принятому обозначению Кэндалла. После исследования системы были сделаны выводы о неэффективности ее работы. Были предложены методы оптимизации работы СМО, но с этими изменениями система перестает быть классической. Основная проблема при исследовании систем массового обслуживания заключается в том, что в реальности они могут быть исследованы с использованием классической теории массового обслуживания только в редких случаях. Потоки входящих и исходящих заявок могут оказаться не простейшими, следовательно, нахождение предельных вероятностей состояний с использованием системы дифференциальных уравнений Колмогорова невозможно, в системе могут присутствовать приоритетные классы, тогда расчет основных показателей СМО также невозможен.
Для оптимизации работы СМО была введена система из двух приоритетных классов и увеличено число обслуживающих каналов. В таком случае целесообразно применить методы имитационного моделирования, например метод Монте-Карло. Основная идея метода заключается в том, что вместо неизвестной случайной величины принимается ее математическое ожидание в достаточно большой серии испытаний. Производится разыгрывание случайной величины (в данном случае это интенсивности входящего и исходящего потоков) изначально равномерно распределенной. Затем осуществляется переход от равномерного распределения к показательному распределению, посредством формул перехода. Была написана программа на языке Visual Basic, реализующая этот метод.
1 Марковские цепи с конечным числом состояний и дискретным временем
Пусть некоторая система S может находиться в одном из состояний конечного (или счетного) множества возможных состояний S>1>, S>2>,…, S>n>, а переход из одного состояния в другое возможен только в определенные дискретные моменты времени t>1>, t>2>, t>3>, называемые шагами.
Если система переходит из одного состояния в другое случайно, то говорят, что имеет место случайный процесс с дискретным временем.
Случайный процесс называется марковским, если вероятность перехода из любого состояния S>i> в любое состояние S>j> не зависит от того, как и когда система S попала в состояние S>i> (т.е. в системе S отсутствует последствие). В таком случае говорят, что функционирование системы S описывается дискретной цепью Маркова.
Переходы системы S в различные состояния удобно изображать с помощью графа состояний (рис. 1).
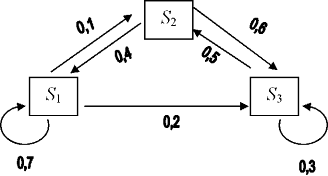
Рисунок 1 – Пример размеченного графа состояний
Вершины графа S>1>,
S>2>,
S>3>
обозначают возможные состояния системы.
Стрелка, направленная из вершины S>i>
в вершину S>j>
обозначает переход >
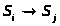 >;
число, стоящее рядом со стрелкой,
обозначает величину вероятности этого
перехода. Стрелка, замыкающаяся на i-той
вершине графа, обозначает, что система
остается в состоянии S>i>
с вероятностью, стоящей у стрелки.
>;
число, стоящее рядом со стрелкой,
обозначает величину вероятности этого
перехода. Стрелка, замыкающаяся на i-той
вершине графа, обозначает, что система
остается в состоянии S>i>
с вероятностью, стоящей у стрелки.
Графу системы, содержащему n вершин, можно поставить в соответствие матрицу NxN, элементами которой являются вероятности переходов p>ij> между вершинами графа. Например, граф на рис. 1 описывается матрицей P:
>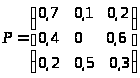 >
>
называемой матрицей вероятностей переходов. Элементы матрицы p>ij> удовлетворяют условиям:
> >
(1)
>
(1)
>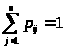 >
(2)
>
(2)
Элементы матрицы p>ij> – дают вероятности переходов в системе за один шаг. Переход
S>i> – S>j> за два шага можно рассматривать как происходящий на первом шаге из S>i> в некоторое промежуточное состояние S>k> и на втором шаге из S>k> в S>i>. Таким образом, для элементов матрицы вероятностей переходов из S>i> в S>j> за два шага получим:
>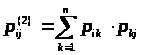 >
>
В общем случае
перехода >
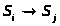 >
за m
шагов для элементов >
>
за m
шагов для элементов >
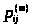 >
матрицы вероятностей переходов
справедлива формула:
>
матрицы вероятностей переходов
справедлива формула:
>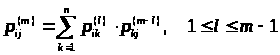 >
(3)
>
(3)
Получим два
эквивалентных выражения для >
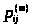 >:
>:
>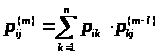 >
>
>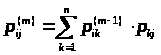 >
>
Пусть система S описывается матрицей вероятностей переходов Р:
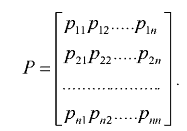
Если обозначить через Р(m) матрицу, элементами которой являются рi вероятности переходов из S>i> в S>j> за m шагов, то справедлива формула
>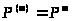 >,
>,
где матрица Р>m> получается умножением матрицы P саму на себя m раз.
Исходное состояние системы характеризуется вектором состояния системы Q(q>i>) (называемым также стохастическим вектором).
>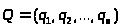 >
>
где q>j>> >- вероятность того, что исходным состоянием системы является S>j> состояние. Аналогично (1) и (2) справедливы соотношения
>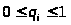 > >
> >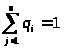 >
>
Обозначим через
>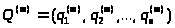 >
>
вектор состояния системы после m шагов, где q>j> – вероятность того, что после m шагов система находится в S>i> состоянии. Тогда справедлива формула
>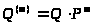 >
>
Если вероятности переходов P>ij> остаются постоянными, то такие марковские цепи называются стационарными. В противном случае марковская цепь называется нестационарной.
2. Марковские цепи с конечным числом состояний и непрерывным временем
Если система S
может переходить в другое состояние
случайным образом в произвольный момент
времени, то говорят о случайном процессе
с непрерывным временем. В отсутствии
последействия такой процесс называется
непрерывной марковской цепью. При этом
вероятности переходов >
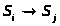 >
для любых i и j
в любой момент времени равны нулю (в
силу непрерывности времени). По этой
причине вместо вероятности перехода >
>
для любых i и j
в любой момент времени равны нулю (в
силу непрерывности времени). По этой
причине вместо вероятности перехода >
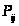 >
вводится величина >
>
вводится величина >
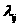 >-
плотность вероятности перехода из
состояния >
>-
плотность вероятности перехода из
состояния >
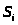 >
в состояние >
>
в состояние >
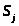 >,
определяемая как предел:
>,
определяемая как предел:
>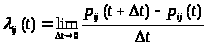 >
>
>
>
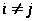 >
>
Если величины >
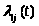 >
не зависят от t, то марковский
процесс называется однородным. Если за
время >
>
не зависят от t, то марковский
процесс называется однородным. Если за
время >
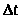 >
система может изменить свое состояние
не более чем один раз, то говорят, что
случайный процесс является ординарным.
Величину >
>
система может изменить свое состояние
не более чем один раз, то говорят, что
случайный процесс является ординарным.
Величину >
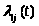 >
называют интенсивностью перехода
системы из S>i>
в S>j>.
На графе состояний системы численные
значения >
>
называют интенсивностью перехода
системы из S>i>
в S>j>.
На графе состояний системы численные
значения >
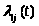 >
ставят рядом со стрелками, показывающими
переходы в вершины графа.
>
ставят рядом со стрелками, показывающими
переходы в вершины графа.
Зная интенсивности переходов можно найти величины p>1>(t), p>2>(t),…, p>n>(t) – вероятности нахождения системы S в состояниях S>1>, S>2>,…, S>n> соответственно. При этом выполняется условие:
>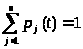 >
>
Распределение
вероятностей состояний системы, которое
можно характеризовать вектором >
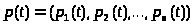 >,
называется стационарным, если оно не
зависит от времени, т.е. все компоненты
вектора >
>,
называется стационарным, если оно не
зависит от времени, т.е. все компоненты
вектора >
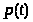 >
являются константами.
>
являются константами.
Состояния S>i>
и Sj называются сообщающимися,
если возможны переходы >
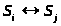 >.
>.
Состояние S>i> называется существенным, если всякое S>j>, достижимое из S>i>, является сообщающимся с S>i>. Состояние S>i> называется несущественным, если оно не является существенным.
Если существуют предельные вероятности состояний системы:
>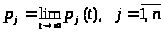 >,
>,
не зависящие от
начального состояния системы, то говорят,
что при >
 >
в системе устанавливается стационарный
режим.
>
в системе устанавливается стационарный
режим.
Система, в которой существуют предельные (финальные) вероятности состояний системы, называется эргодической, а протекающий в ней случайный процесс эргодическим.
Теорема 1. Если S>i>
– несущественное состояние, то >
 >
т.е. при >
>
т.е. при >
 >
система выходит из любого несущественного
состояния.
>
система выходит из любого несущественного
состояния.
Теорема 2. Чтобы система с конечным числом состояний имела единственное предельное распределение вероятностей состояний, необходимо и достаточно, чтобы все ее существенные состояния сообщались между собой.
Если случайный процесс, происходящий в системе с дискретными состояниями является непрерывной марковской цепью, то для вероятностей p>1>(t), р>2>(t),…, p>n>(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова. При составлении уравнений удобно пользоваться графом состояний системы. В левой части каждого из них стоит производная вероятности какого-то (j-го) состояния. В правой части – сумма произведений вероятностей всех состояний, из которых возможен переход в данное состояние, на интенсивности соответствующих потоков, минус суммарная интенсивность всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния.
3 Процессы рождения и гибели
Так называется широкий класс случайных процессов, происходящих в системе, размеченный граф состояний которой изображен на рис. 3.
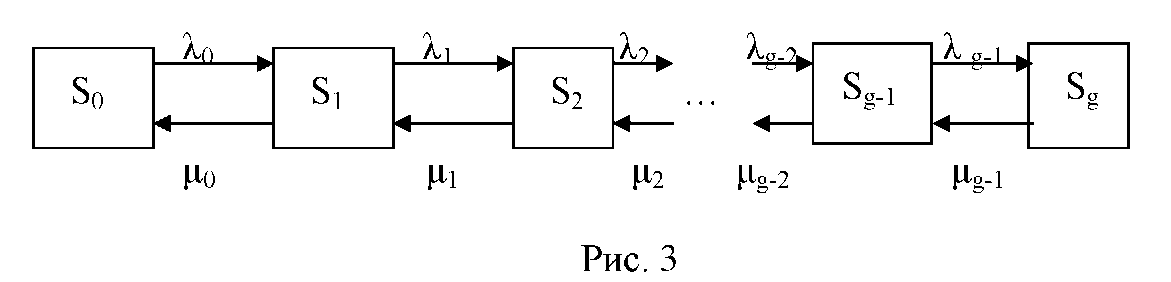
Рисунок 2 – Граф состояний для процессов гибели и размножения
Здесь величины >
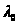 >,
>
>,
>
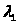 >,…,
>
>,…,
>
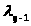 >
– интенсивности переходов системы из
состояния в состояние слева направо,
можно интерпретировать как интенсивности
рождения (возникновения заявок) в
системе. Аналогично, величины >
>
– интенсивности переходов системы из
состояния в состояние слева направо,
можно интерпретировать как интенсивности
рождения (возникновения заявок) в
системе. Аналогично, величины >
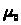 >,>
>,>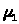 >,…,>
>,…,>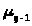 >
– интенсивности переходов системы из
состояния в состояние справа налево,
можно интерпретировать как интенсивности
гибели (выполнения заявок) в системе.
>
– интенсивности переходов системы из
состояния в состояние справа налево,
можно интерпретировать как интенсивности
гибели (выполнения заявок) в системе.
Поскольку все состояния являются сообщающимися и существенными, существует (в силу теоремы 2) предельное (финальное) распределение вероятностей состояний. Получим формулы для финальных вероятностей состояний системы.
В стационарных условиях для каждого состояния поток, входящий в данное состояние должен равняться потоку, исходящему из данного состояния. Таким образом, имеем:
Для состояния S>0>:
>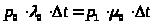 >
>
Следовательно:
>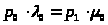 >
>
Для состояния S>1>:
>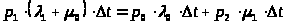 >
>
Следовательно:
>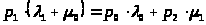 >
>
С учетом того, что
>
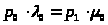 >:
>:
>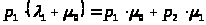 >
>
>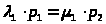 >
>
Аналогично получаем уравнения для остальных состояний системы. В результате получим систему уравнений:
>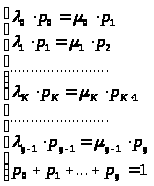 >
>
Решение этой системы будет иметь вид:
>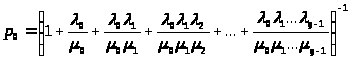 >
(4)
>
(4)
>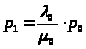 >,
>
>,
>
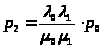 >,…,
>
>,…,
>
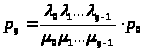 >
(5)
>
(5)
4. Основные понятия и классификация систем массового обслуживания
Заявкой (или требованием) называется спрос на удовлетворение какой-либо потребности (далее потребности предполагаются однотипными). Выполнение заявки называется обслуживанием заявки.
Системой массового обслуживания (СМО) называется любая система для выполнения заявок, поступающих в неё в случайные моменты времени.
Поступление заявки в СМО называется событием. Последовательность событий, заключающихся в поступлении заявок в СМО, называется входящим потоком заявок. Последовательность событий, заключающихся в выполнении заявок в СМО, называется выходящим потоком заявок.
Поток заявок называется простейшим, если он удовлетворяет следующим условиям:
1) отсутствие последействия, т.е. заявки поступают независимо друг от друга;
2) стационарность, т.е. вероятность поступления данного числа заявок на любом временном отрезке [t>1>; t>2>] зависит лишь от величины этого отрезка и не зависит от значения t>1>, что позволяет говорить о среднем числе заявок за единицу времени, λ, называемом интенсивностью потока заявок;
3) ординарность, т.е. в любой момент времени в СМО поступает лишь одна заявка, а поступление одновременно двух и более заявок пренебрежимо мало.
Для простейшего потока вероятность p>i>(t) поступления в СМО ровно i заявок за время t вычисляется по формуле:
>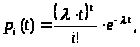 > (6)
> (6)
т.е. вероятности распределены по закону Пуассона с параметром λt. По этой причине простейший поток называется также пуассоновским потоком.
Функция распределения
F(t) случайного
интервала времени T между
двумя последовательными заявками по
определению равна >
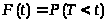 >.
Но >
>.
Но >
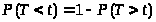 >,
где >
>,
где >
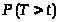 >
– вероятность того, что следующая после
последней заявки поступит в СМО по
истечении времени t, т.е.
за время t в СМО не поступит
ни одна заявка. Но вероятность этого
события находится из (6) при i
= 0. Таким образом:
>
– вероятность того, что следующая после
последней заявки поступит в СМО по
истечении времени t, т.е.
за время t в СМО не поступит
ни одна заявка. Но вероятность этого
события находится из (6) при i
= 0. Таким образом:
>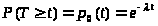 >
>
>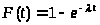 >
(7)
>
(7)
Плотность вероятности f(t) случайной величины T определяется формулой:
>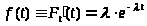 > ,
>
> ,
>
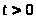 >
>
Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины T равны соответственно:
>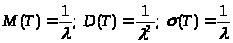 >
>
Каналом обслуживания называется устройство в СМО, обслуживающее заявку. СМО, содержащее один канал обслуживания, называется одноканальной, а содержащее более одного канала обслуживания – многоканальной.
Если заявка, поступающая в СМО, может получить отказ в обслуживании (в силу занятости всех каналов обслуживания) и в случае отказа вынуждена покинуть СМО, то такая СМО называется СМО с отказами.
Если в случае отказа в обслуживании заявки могут вставать в очередь, то такие СМО называются СМО с очередью (или с ожиданием). При этом различают СМО с ограниченной и неограниченной очередью. Очередь может быть ограничена как по количеству мест, так и по времени ожидания. Различают СМО открытого и замкнутого типа. В СМО открытого типа поток заявок не зависит от СМО. В СМО замкнутого типа обслуживается ограниченный круг клиентов, а число заявок может существенно зависеть от состояния СМО (например, бригада слесарей – наладчиков, обслуживающих станки на заводе).
СМО могут также различаться по дисциплине обслуживания.
Если в СМО нет приоритета, то заявки отбираются из очереди в канал по различным правилам.
Первым пришел – первым обслужен (FCFS – First Came – First Served)
Последним пришел – первым обслужен (LCFS – Last Came – First Served)
Первоочередное обслуживание требований с кратчайшей длительностью обслуживания (SPT/SJE)
Первоочередное обслуживание требований с кратчайшей длительностью дообслуживания (SRPT)
Первоочередное обслуживание требований с кратчайшей средней длительностью обслуживания (SEPT)
Первоочередное обслуживание требований с кратчайшей средней длительностью дообслуживания (SERPT)
Приоритеты бывают двух типов – абсолютный и относительный.
Если требование в процессе обслуживания может быть удалено из канала и возвращено в очередь (либо вовсе покидает СМО) при поступлении требования с более высоким приоритетом, то система работает с абсолютным приоритетом. Если обслуживание любого требования, находящегося в канале не может быть прервано, то СМО работает с относительным приоритетом. Существуют также приоритеты, осуществляемые с помощью конкретного правила или набора правил. Примером может служить приоритет, изменяющийся с течением времени.
СМО описываются некоторыми параметрами, которые характеризуют эффективность работы системы.
> >
– число каналов в СМО;
>
– число каналов в СМО;
>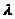 >
– интенсивность поступления в
СМО заявок;
>
– интенсивность поступления в
СМО заявок;
>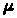 >
– интенсивность обслуживания
заявок;
>
– интенсивность обслуживания
заявок;
>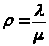 >
– коэффициент загрузки СМО;
>
– коэффициент загрузки СМО;
> >
– число мест в очереди;
>
– число мест в очереди;
>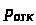 >
– вероятность отказа в обслуживании
поступившей в СМО заявки;
>
– вероятность отказа в обслуживании
поступившей в СМО заявки;
>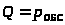 >
– вероятность обслуживания
поступившей в СМО заявки (относительная
пропускная способность СМО);
>
– вероятность обслуживания
поступившей в СМО заявки (относительная
пропускная способность СМО);
При этом:
>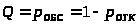 >
(8)
>
(8)
А – среднее число заявок, обслуживаемых в СМО в единицу времени (абсолютная пропускная способность СМО)
>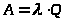 >
(9)
>
(9)
>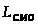 >
– среднее число заявок, находящихся
в СМО
>
– среднее число заявок, находящихся
в СМО
>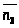 >
– среднее число каналов в СМО,
занятых обслуживанием заявок. В тоже
время это >
>
– среднее число каналов в СМО,
занятых обслуживанием заявок. В тоже
время это >
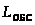 >
– среднее число заявок, обслуживаемых
в СМО за единицу времени. Величина >
>
– среднее число заявок, обслуживаемых
в СМО за единицу времени. Величина >
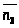 >
определяется как математическое ожидание
случайного числа занятых обслуживанием
n каналов.
>
определяется как математическое ожидание
случайного числа занятых обслуживанием
n каналов.
>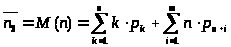 >,
(10)
>,
(10)
где >
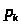 >
– вероятность нахождения системы в S>k>
состоянии.
>
– вероятность нахождения системы в S>k>
состоянии.
>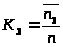 >
– коэффициент занятости каналов
>
– коэффициент занятости каналов
>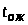 >
– среднее время ожидания заявки
в очереди
>
– среднее время ожидания заявки
в очереди
>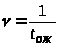 >
– интенсивность ухода заявок
из очереди
>
– интенсивность ухода заявок
из очереди
>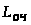 >
– среднее число заявок в очереди.
Определяется как математическое ожидание
случайной величины m –
числа заявок, состоящих в очереди
>
– среднее число заявок в очереди.
Определяется как математическое ожидание
случайной величины m –
числа заявок, состоящих в очереди
>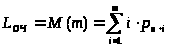 >
(11)
>
(11)
Здесь >
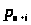 >
– вероятность нахождения в очереди i
заявок;
>
– вероятность нахождения в очереди i
заявок;
>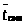 >
– среднее время пребывания
заявки с СМО
>
– среднее время пребывания
заявки с СМО
>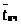 >
– среднее время пребывания
заявки в очереди
>
– среднее время пребывания
заявки в очереди
Для открытых СМО справедливы соотношения:
>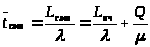 >
(12)
>
(12)
>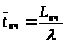 >
(13)
>
(13)
Эти соотношения называются формулами Литтла и применяются только для стационарных потоков заявок и обслуживания.
Рассмотрим некоторые конкретные типы СМО. При этом будет предполагаться, что плотность распределения промежутка времени между двумя последовательными событиями в СМО имеет показательное распределение (7), а все потоки являются простейшими.
5. Основные типы открытых систем массового обслуживания
5.1 Одноканальная система массового обслуживания с отказами
Размеченный граф состояний одноканальной СМО представлен на рисунке 3.
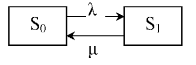
Рисунок 3 – Граф состояний одноканальной СМО
Здесь >
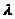 >
и >
>
и >
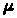 >
– интенсивность потока заявок и
выполнения заявок соответственно.
Состояние системы S>o>
обозначает, что канал свободен, а S>1>
– что канал занят обслуживанием заявки.
>
– интенсивность потока заявок и
выполнения заявок соответственно.
Состояние системы S>o>
обозначает, что канал свободен, а S>1>
– что канал занят обслуживанием заявки.
Система дифференциальных уравнений Колмогорова для такой СМО имеет вид:
>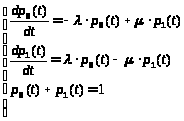 >
>
где p>o>(t) и p>1>(t) – вероятности нахождения СМО в состояниях So и S1 соответственно. Уравнения для финальных вероятностей p>o> и p>1> получим, приравнивая нулю производные в первых двух уравнениях системы. В результате получим:
>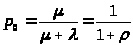 >
(14)
>
(14)
>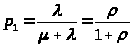 >
(15)
>
(15)
Вероятность p>0> по своему смыслу есть вероятность обслуживания заявки p>обс>, т. к. канал является свободным, а вероятность р>1> по своему смыслу является вероятностью отказа в обслуживании поступающей в СМО заявки р>отк>, т. к. канал занят обслуживанием предыдущей заявки.
5.2 Многоканальная система массового обслуживания с отказами
Пусть СМО содержит
n
каналов, интенсивность входящего потока
заявок равна >
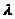 >,
а интенсивность обслуживания заявки
каждым каналом равна >
>,
а интенсивность обслуживания заявки
каждым каналом равна >
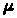 >.
Размеченный граф состояний системы
изображён на рисунке 4.
>.
Размеченный граф состояний системы
изображён на рисунке 4.

Рисунок 4 – Граф состояний многоканальной СМО с отказами
Состояние S>0>
означает, что все каналы свободны,
состояние S>k>
(k
= 1, n)
означает, что обслуживанием заявок
заняты k
каналов. Переход из одного состояния в
другое соседнее правое происходит
скачкообразно под воздействием входящего
потока заявок интенсивностью >
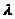 >
независимо от числа работающих каналов
(верхние стрелки). Для перехода системы
из одного состояния в соседнее левое
неважно, какой именно канал освободится.
Величина >
>
независимо от числа работающих каналов
(верхние стрелки). Для перехода системы
из одного состояния в соседнее левое
неважно, какой именно канал освободится.
Величина >
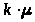 >
характеризует интенсивность обслуживания
заявок при работе в СМО k
каналов (нижние стрелки).
>
характеризует интенсивность обслуживания
заявок при работе в СМО k
каналов (нижние стрелки).
Сравнивая графы на
рис. 3 и на рис. 5 легко увидеть, что
многоканальная СМО с отказами является
частным случаем системы рождения и
гибели, если в последней принять >
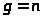 >
и
>
и
>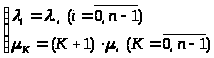 >
(16)
>
(16)
При этом для нахождения финальных вероятностей можно воспользоваться формулами (4) и (5). С учётом (16) получим из них:
>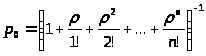 >
(17)
>
(17)
>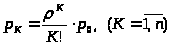 >
(18)
>
(18)
Формулы (17) и (18) называются формулами Эрланга – основателя теории массового обслуживания.
Вероятность отказа в обслуживании заявки р>отк> равна вероятности того, что все каналы заняты, т.е. система находится в состоянии S>n>. Таким образом,
>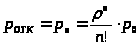 >
(19)
>
(19)
Относительную пропускную способность СМО найдём из (8) и (19):
> >
(20)
>
(20)
Абсолютную пропускную способность найдём из (9) и (20):
>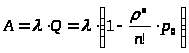 >
>
Среднее число занятых
обслуживанием каналов можно найти по
формуле (10), однако сделаем это проще.
Так как каждый занятый канал в единицу
времени обслуживает в среднем >
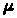 >
заявок, то >
>
заявок, то >
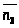 >
можно найти по формуле:
>
можно найти по формуле:
>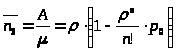 >
>
5.3 Одноканальная система массового обслуживания с ограниченной длиной очереди
В СМО с ограниченной очередью число мест m в очереди ограничено. Следовательно, заявка, поступившая в момент времени, когда все места в очереди заняты, отклоняется и покидает СМО. Граф такой СМО представлен на рисунке 5.

Рисунок 5 – Граф состояний одноканальной СМО с ограниченной очередью
Состояния СМО представляются следующим образом:
S>0> – канал обслуживания свободен,
S>1> – канал обслуживания занят, но очереди нет,
S>2> – канал обслуживания занят, в очереди одна заявка,
S>k>>+1> – канал обслуживания занят, в очереди k заявок,
S>m>>+1> – канал обслуживания занят, все m мест в очереди заняты.
Для получения
необходимых формул можно воспользоваться
тем обстоятельством, что СМО на рисунок
5 является частным случаем системы
рождения и гибели, представленной на
рисунке 2, если в последней принять >
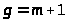 >
и
>
и
>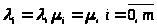 >
(21)
>
(21)
>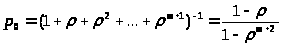 >
(22)
>
(22)
>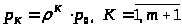 >
(23)
>
(23)
Выражения для финальных вероятностей состояний рассматриваемой СМО можно найти из (4) и (5) с учётом (21). В результате получим:
При р = 1 формулы (22), (23) принимают вид
При m = 0 (очереди нет) формулы (22), (23) переходят в формулы (14) и (15) для одноканальной СМО с отказами.
Поступившая в СМО заявка получает отказ в обслуживании, если СМО находится в состоянии S>m>>+1>, т.е. вероятность отказа в обслуживании заявки равна:
>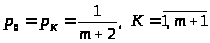 >
>
>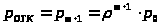 >
>
Относительная пропускная способность СМО равна:
>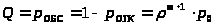 >
>
Абсолютная пропускная способность равна:
>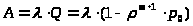 >
>
Среднее число заявок, стоящих в очереди L>оч>, находится по формуле
>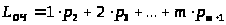 >
>
и может быть записано в виде:
>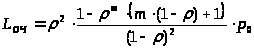 >
(24)
>
(24)
При >
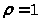 >
формула (24) принимает вид:
>
формула (24) принимает вид:
>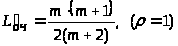 >
>
>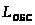 >
– среднее число заявок, находящихся
в СМО, находится по формуле(10)
>
– среднее число заявок, находящихся
в СМО, находится по формуле(10)
>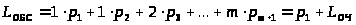 >
>
и может быть записано в виде:
>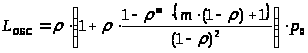 >
(25)
>
(25)
При >
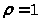 >,
из (25) получим:
>,
из (25) получим:
>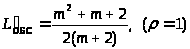 >
>
Среднее время пребывания заявки в СМО и в очереди находится по формулам (12) и (13) соответственно.
5.4 Одноканальная система массового обслуживания с неограниченной очередью
Примером такой СМО может служить директор предприятия, вынужденный рано или поздно решать вопросы, относящиеся к его компетенции, или, например, очередь в булочной с одним кассиром. Граф такой СМО изображён на рисунке 6.

Рисунок 6 – Граф состояний одноканальной СМО с неограниченной очередью
Все характеристики
такой СМО можно получить из формул
предыдущего раздела, полагая в них >
 >.
При этом необходимо различать два
существенно разных случая: а) >
>.
При этом необходимо различать два
существенно разных случая: а) >
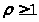 >;
б) >
>;
б) >
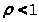 >.
В первом случае, как это видно из формул
(22), (23), р>0>
= 0 и p>k>
= 0 (при всех конечных значениях k).
Это означает, что при >
>.
В первом случае, как это видно из формул
(22), (23), р>0>
= 0 и p>k>
= 0 (при всех конечных значениях k).
Это означает, что при >
 >
очередь неограниченно возрастает, т.е.
этот случай практического интереса не
представляет.
>
очередь неограниченно возрастает, т.е.
этот случай практического интереса не
представляет.
Рассмотрим случай,
когда >
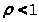 >.
Формулы (22) и (23) при этом запишутся в
виде:
>.
Формулы (22) и (23) при этом запишутся в
виде:
>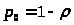 >
>
>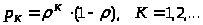 >
>
Поскольку в СМО отсутствует ограничение на длину очереди, то любая заявка может быть обслужена, т.е. относительная пропускная способность равна:
>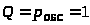 >
>
Абсолютная пропускная способность равна:
>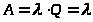 >
>
Среднее число заявок
в очереди получим из формулы (24) при >
 >:
>:
>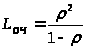 >
>
Среднее число обслуживаемых заявок есть:
>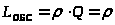 >
>
Среднее число заявок, находящихся в СМО:
>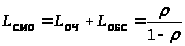 >
>
Среднее время пребывания заявки в СМО и в очереди определяются формулами (12) и (13).
5.5 Многоканальная система массового обслуживания с ограниченной очередью
Пусть на вход СМО,
имеющей >
 >
каналов обслуживания, поступает
пуассоновский поток заявок с интенсивностью
>
>
каналов обслуживания, поступает
пуассоновский поток заявок с интенсивностью
>
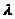 >.
Интенсивность обслуживания заявки
каждым каналом равна >
>.
Интенсивность обслуживания заявки
каждым каналом равна >
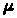 >,
а максимальное число мест в очереди
равно >
>,
а максимальное число мест в очереди
равно >
 >.
>.
Граф такой системы представлен на рисунке 7.
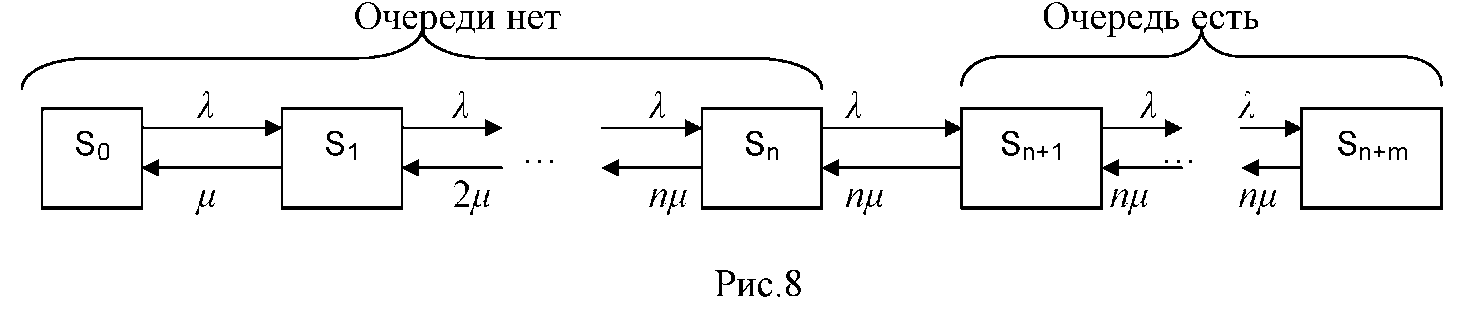
Рисунок 7 – Граф состояний многоканальной СМО с ограниченной очередью
>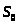 >
– все каналы свободны, очереди
нет;
>
– все каналы свободны, очереди
нет;
>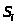 >
– заняты l
каналов (l = 1, n),
очереди нет;
>
– заняты l
каналов (l = 1, n),
очереди нет;
>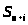 >-
заняты все n каналов, в
очереди находится i
заявок (i = 1, m).
>-
заняты все n каналов, в
очереди находится i
заявок (i = 1, m).
Сравнение графов на рисунке 2 и рисунке 7 показывает, что последняя система является частным случаем системы рождения и гибели, если в ней сделать следующие замены (левые обозначения относятся к системе рождения и гибели):
>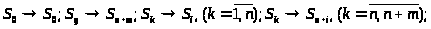 >
>
>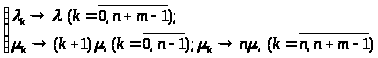 >
>
Выражения для финальных вероятностей легко найти из формул (4) и (5). В результате получим:
>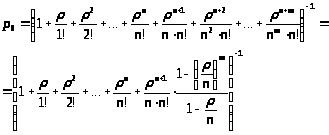 >
(26)
>
(26)
>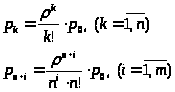 >
>
Образование очереди
происходит, когда в момент поступления
в СМО очередной заявки все каналы заняты,
т.е. в системе находятся либо n,
либо (n+1),…, либо (n
+ m – 1) заявок. Т.к. эти
события несовместны, то вероятность
образования очереди p>оч>
равна сумме соответствующих вероятностей
>
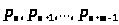 >:
>:
>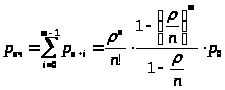 >
(27)
>
(27)
Отказ в обслуживании заявки происходит, когда все m мест в очереди заняты, т.е.:
>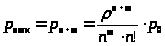 >
>
Относительная пропускная способность равна:
>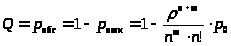 >
>
Абсолютная пропускная способность:
>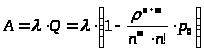 >
>
Среднее число заявок, находящихся в очереди, определяется по формуле (11) и может быть записано в виде:
>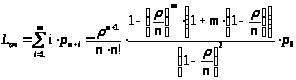 >
(28)
>
(28)
Среднее число заявок, обслуживаемых в СМО, может быть записано в виде:
>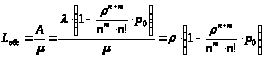 >
>
Среднее число заявок, находящихся в СМО:
>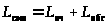 >
>
Среднее время пребывания заявки в СМО и в очереди определяется формулами (12) и (13).
5.6 Многоканальная система массового обслуживания с неограниченной очередью
Граф такой СМО
изображен на рисунке 8 и получается из
графа на рисунке 7 при >
 >.
>.

Рисунок 8 – Граф состояний многоканальной СМО с неограниченной очередью
Формулы для финальных
вероятностей можно получить из формул
для n-канальной
СМО с ограниченной очередью при >
 >.
При этом следует иметь в виду, что при
>
>.
При этом следует иметь в виду, что при
>
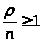 >
вероятность р>0>
= р>1>=…=
p>n>
= 0, т.е. очередь неограниченно возрастает.
Следовательно, этот случай практического
интереса не представляет и ниже
рассматривается лишь случай >
>
вероятность р>0>
= р>1>=…=
p>n>
= 0, т.е. очередь неограниченно возрастает.
Следовательно, этот случай практического
интереса не представляет и ниже
рассматривается лишь случай >
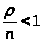 >.
При >
>.
При >
 >
из (26) получим:
>
из (26) получим:
>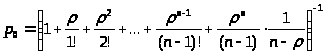 >
>
Формулы для остальных вероятностей имеют тот же вид, что и для СМО с ограниченной очередью:
>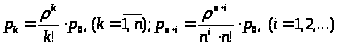 >
>
Из (27) получим выражение для вероятности образования очереди заявок:
>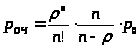 >
>
Поскольку очередь не ограничена, то вероятность отказа в обслуживании заявки:
>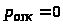 >
>
Относительная пропускная способность:
>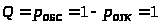 >
>
Абсолютная пропускная способность:
>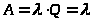 >
>
Из формулы (28) при >
 >
получим выражение для среднего числа
заявок в очереди:
>
получим выражение для среднего числа
заявок в очереди:
>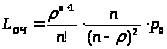 >
>
Среднее число обслуживаемых заявок определяется формулой:
>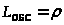 >
>
Среднее время пребывания в СМО и в очереди определяется формулами (12) и (13).
5.7 Многоканальная система массового обслуживания с ограниченной очередью и ограниченным временем ожидания в очереди
Отличие такой СМО
от СМО, рассмотренной в подразделе 5.5,
состоит в том, что время ожидания
обслуживания, когда заявка находится
в очереди, считается случайной величиной,
распределённой по показательному закону
с параметром >
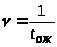 >,
где >
>,
где >
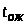 >
– среднее время ожидания заявки в
очереди, а >
>
– среднее время ожидания заявки в
очереди, а >
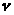 >
– имеет смысл интенсивности потока
ухода заявок из очереди. Граф такой СМО
изображён на рисунке 9.
>
– имеет смысл интенсивности потока
ухода заявок из очереди. Граф такой СМО
изображён на рисунке 9.
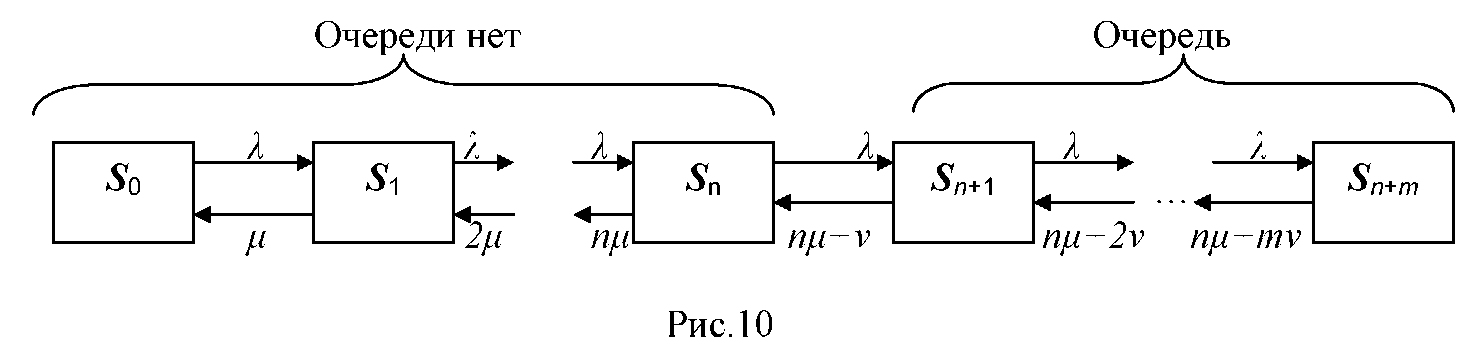
Рисунок 9 – Граф многоканальной СМО с ограниченной очередью и ограниченным временем ожидания в очереди
Остальные обозначения имеют здесь тот же смысл, что и в подразделе.
Сравнение графов на рис. 3 и 9 показывает, что последняя система является частным случаем системы рождения и гибели, если в ней сделать следующие замены (левые обозначения относятся к системе рождения и гибели):
>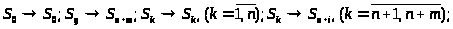 >
>
>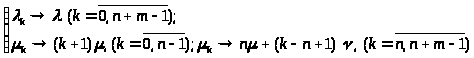 >
(29)
>
(29)
Выражения для финальных вероятностей легко найти из формул (4) и (5) с учетом (29). В результате получим:
>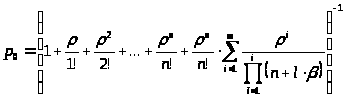 >
>
>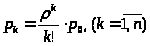 >
>
>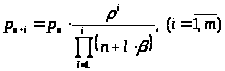 >,
>,
где >
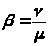 >.
Вероятность образования очереди
определяется формулой:
>.
Вероятность образования очереди
определяется формулой:
>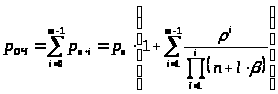 >
>
Отказ в обслуживании заявки происходит, когда все m мест в очереди заняты, т.е. вероятность отказа в обслуживании:
>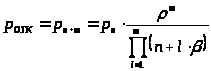 >
>
Относительная пропускная способность:
>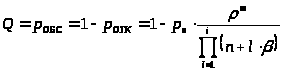 >
>
Абсолютная пропускная способность:
>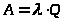 >
>
Среднее число заявок, находящихся в очереди, находится по формуле (11) и равно:
>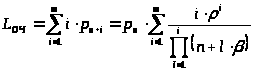 >
>
Среднее число заявок, обслуживаемых в СМО, находится по формуле (10) и равно:
>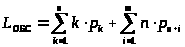 >
>
Среднее время пребывания заявки в СМО складывается из среднего времени ожидания в очереди и среднего времени обслуживания заявки:
>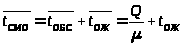 >
>
6. Метод Монте-Карло
6.1 Основная идея метода
Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину Х, математическое ожидание которой равно а: М(Х)=а.
Практически же
поступают так: производят n
испытаний, в результате которых получают
n возможных значений Х;
вычисляют их среднее арифметическое >
 >
и принимают >
>
и принимают >
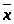 >
в качестве оценки (приближённого
значения) a*
искомого числа a:
>
в качестве оценки (приближённого
значения) a*
искомого числа a:
>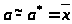 >.
>.
Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний.
6.2 Разыгрывание непрерывной случайной величины
Пусть необходимо
получить значения случайной величины
>
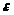 >,
распределенной в интервале >
>,
распределенной в интервале >
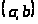 >
с плотностью >
>
с плотностью >
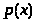 >.
Докажем, что значения >
>.
Докажем, что значения >
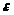 >
можно найти из уравнения
>
можно найти из уравнения
>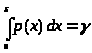 >,
(30)
>,
(30)
где >
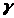 >
– случайная величина, равномерно
распределенная на интервале >
>
– случайная величина, равномерно
распределенная на интервале >
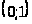 >.
>.
Т.е. выбрав очередное
значение >
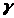 >
надо решить уравнение (30) и найти очередное
значение >
>
надо решить уравнение (30) и найти очередное
значение >
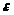 >.
Для доказательства рассмотрим функцию:
>.
Для доказательства рассмотрим функцию:
>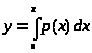 >
>
Имеем общие свойства плотности вероятности:
>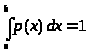 >
(31)
>
(31)
>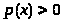 >
(32)
>
(32)
Из (31) и (32) следует,
что >
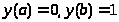 >,
а производная >
>,
а производная >
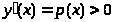 >.
>.
Значит, функция >
 >
монотонно возрастает от 0 до 1. И любая
прямая >
>
монотонно возрастает от 0 до 1. И любая
прямая >
 >,
где >
>,
где >
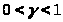 >,
пересекает график функции >
>,
пересекает график функции >
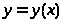 >
в единственной точке, абсциссу которой
мы и принимаем за >
>
в единственной точке, абсциссу которой
мы и принимаем за >
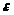 >.
Таким образом, уравнение (30) всегда имеет
одно и только одно решение.
>.
Таким образом, уравнение (30) всегда имеет
одно и только одно решение.
Выберем теперь
произвольный интервал >
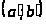 >,
содержащийся внутри >
>,
содержащийся внутри >
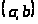 >.
Точкам этого интервала отвечают ординаты
кривой, удовлетворяющие неравенству
>
>.
Точкам этого интервала отвечают ординаты
кривой, удовлетворяющие неравенству
>
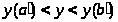 >.
Поэтому, если >
>.
Поэтому, если >
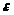 >
принадлежит интервалу >
>
принадлежит интервалу >
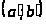 >,
то
>,
то
>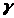 >
принадлежит интервалу >
>
принадлежит интервалу >
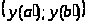 >,
и наоборот. Значит: >
>,
и наоборот. Значит: >
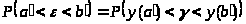 >.
Т.к. >
>.
Т.к. >
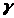 >
равномерно распределена в >
>
равномерно распределена в >
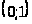 >,
то
>,
то
>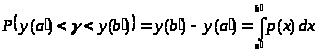 >,
а это как раз и означает, что случайная
величина >
>,
а это как раз и означает, что случайная
величина >
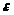 >,
являющаяся корнем уравнения (30) имеет
плотность вероятностей >
>,
являющаяся корнем уравнения (30) имеет
плотность вероятностей >
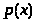 >.
>.
6.3 Случайная величина с экспоненциальным распределением
Простейшим потоком
(или потоком Пуассона) называется такой
поток заявок, когда промежуток времени
>
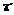 >
между двумя последовательными заявками
есть случайная величина, распределенная
на интервале >
>
между двумя последовательными заявками
есть случайная величина, распределенная
на интервале >
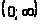 >
с плотностью
>
с плотностью
>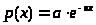 >
>
Вычислим математическое
ожидание: >
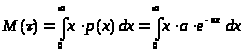 >
>
После интегрирования по частям, получим:
>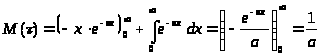 >.
>.
Параметр >
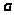 >
есть интенсивность потока заявок.
>
есть интенсивность потока заявок.
Формулу для розыгрыша
>
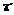 >
получим из уравнения (30), которое в данном
случае запишется так: >
>
получим из уравнения (30), которое в данном
случае запишется так: >
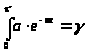 >.
>.
Вычислив интеграл,
стоящий слева, получим соотношение >
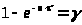 >.
Отсюда, выражая >
>.
Отсюда, выражая >
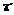 >,
получим:
>,
получим:
>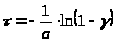 >
(33)
>
(33)
Т.к. величина >
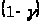 >
распределена также как и >
>
распределена также как и >
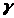 >,
следовательно, формулу (33) можно записать
в виде:
>,
следовательно, формулу (33) можно записать
в виде:
>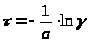 >
(34)
>
(34)
7 Исследование системы массового обслуживания
7.1 Проверка гипотезы о показательном распределении
Исследуемое мной предприятие представляет собой двухканальную систему массового обслуживания с ограниченной очередью. На вход поступает пуассоновский поток заявок с интенсивностью λ. Интенсивности обслуживания заявок каждым из каналов μ, а максимальное число мест в очереди m.
Начальные параметры:
>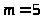 >
>
>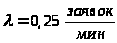 >
>
Время обслуживания
заявок имеет эмпирическое распределение,
указанное ниже и имеет среднее значение
>
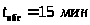 >.
>.
>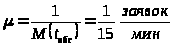 >
>
Мной были проведены контрольные замеры времени обработки заявок, поступающих в данную СМО. Чтобы приступить к исследованию, необходимо установить по этим замерам закон распределения времени обработки заявок.
Таблица 6.1 – Группировка заявок по времени обработки
|
Количество заявок |
22 |
25 |
23 |
16 |
14 |
10 |
8 |
4 |
|
Время обработки, мин |
0–5 |
5–10 |
10–15 |
15–20 |
20–25 |
25–30 |
30–35 |
35–40 |
Выдвигается гипотеза о показательном распределении генеральной совокупности.
Для того чтобы, при
уровне значимости >
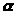 >
проверить гипотезу о том, что непрерывная
случайная величина распределена по
показательному закону, надо:
>
проверить гипотезу о том, что непрерывная
случайная величина распределена по
показательному закону, надо:
1) Найти по заданному
эмпирическому распределению выборочную
среднюю >
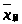 >.
Для этого, каждый i – й
интервал заменяем его серединой >
>.
Для этого, каждый i – й
интервал заменяем его серединой >
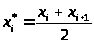 >
и составляем последовательность
равноотстоящих вариант и соответствующих
им частот.
>
и составляем последовательность
равноотстоящих вариант и соответствующих
им частот.
2) Принять в качестве оценки параметра λ показательного распределения величину, обратную выборочной средней:
>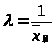 >
>
3) Найти вероятности попадания X в частичные интервалы по формуле:
>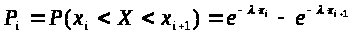 >
>
4) Вычислить теоретические частоты:
>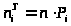 >,
>,
где >
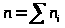 >-
объем выборки
>-
объем выборки
5) Сравнить эмпирические
и теоретические частоты с помощью
критерия Пирсона, приняв число степеней
свободы >
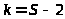 >,
где S – число интервалов
первоначальной выборки.
>,
где S – число интервалов
первоначальной выборки.
Таблица 6.2 – Группировка заявок по времени обработки с усредненным временным интервалом
|
Количество заявок |
22 |
25 |
23 |
16 |
14 |
10 |
8 |
4 |
|
Время обработки, мин |
2,5 |
7,5 |
12,5 |
17,5 |
22,5 |
27,5 |
32,5 |
37,5 |
Найдем выборочную среднюю:
>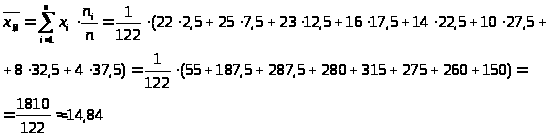 >
>
2) Примем в качестве
оценки параметра λ
экспоненциального распределения
величину, равную >
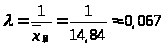 >.
Тогда:
>.
Тогда:
>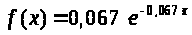 >
(>
>
(>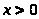 >)
>)
3) Найдем вероятности попадания X в каждый из интервалов по формуле:
>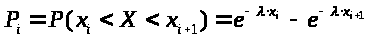 >
>
Для первого интервала:
>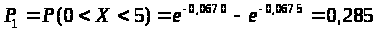 >
>
Для второго интервала:
>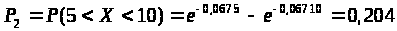 >
>
Для третьего интервала:
>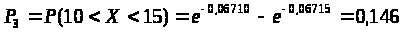 >
>
Для четвертого интервала:
>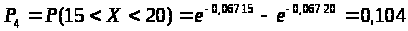 >
>
Для пятого интервала:
>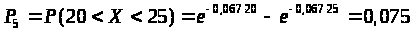 >
>
Для шестого интервала:
>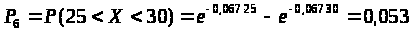 >
>
Для седьмого интервала:
>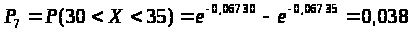 >
>
Для восьмого интервала:
>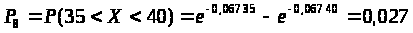 >
>
4) Вычислим теоретические частоты:
>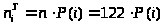 >
>
Результаты вычислений
заносим в таблицу. Сравниваем эмпирические
>
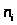 >
и теоретические >
>
и теоретические >
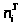 >
частоты с помощью критерия Пирсона.
>
частоты с помощью критерия Пирсона.
Для этого вычислим
разности >
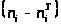 >,
их квадраты, затем отношения >
>,
их квадраты, затем отношения >
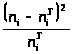 >.
Суммируя значения последнего столбца,
находим наблюдаемое значение критерия
Пирсона. По таблице критических точек
распределения >
>.
Суммируя значения последнего столбца,
находим наблюдаемое значение критерия
Пирсона. По таблице критических точек
распределения >
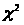 >
при уровне значимости >
>
при уровне значимости >
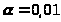 >
и числу степеней свободы >
>
и числу степеней свободы >
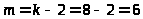 >
находим критическую точку >
>
находим критическую точку >
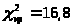 >
>
Таблица 6.3 – Результаты вычислений
|
i |
> |
> |
> |
> |
> |
> |
|
1 |
22 |
0,285 |
34,77 |
-12,77 |
163,073 |
4,690 |
|
2 |
25 |
0,204 |
24,888 |
0,112 |
0,013 |
0,001 |
|
3 |
23 |
0,146 |
17,812 |
5,188 |
26,915 |
1,511 |
|
4 |
16 |
0,104 |
12,688 |
3,312 |
10,969 |
0,865 |
|
5 |
14 |
0,075 |
9,15 |
4,85 |
23,523 |
2,571 |
|
6 |
10 |
0,053 |
6,466 |
3,534 |
12,489 |
1,932 |
|
7 |
8 |
0,038 |
4,636 |
3,364 |
11,316 |
2,441 |
|
8 |
4 |
0,027 |
3,294 |
0,706 |
0,498 |
0,151 |
|
122 |
> |
Т.к. >
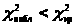 >,
то нет оснований отвергнуть гипотезу
о распределении X по
показательному закону. Другими словами,
данные наблюдений согласуются с этой
гипотезой.
>,
то нет оснований отвергнуть гипотезу
о распределении X по
показательному закону. Другими словами,
данные наблюдений согласуются с этой
гипотезой.
7.2 Расчет основных показателей системы массового обслуживания
Данная система представляет собой частный случай системы гибели и размножения.
Граф данной системы:
0100090000031602000002009601000000009601000026060f002203574d46430100000000000100ef380000000001000000000300000000000000030000010000006c0000000000000000000000350000006f0000000000000000000000cf3a0000670c000020454d46000001000003000010000000020000000000000000000000000000005e130000681b0000d200000029010000000000000000000000000000ef33030028880400160000000c000000180000000a0000001000000000000000000000000900000010000000e20d0000ef020000520000007001000001000000a4ffffff00000000000000000000000090010000000000cc04400022430061006c00690062007200690000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000110080ae110010000000e4b1110064af110052516032e4b11100dcae1100100000004cb01100c8b1110024516032e4b11100dcae11002000000049642f31dcae1100e4b1110020000000ffffffff7c1cd400d0642f31ffffffffffff0180ffff0180efff0180ffffffff0000000000080000000800004300000001000000000000005802000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000a4af1100dee32e31e88d083204b3110010af11009c38273106000000010000004caf11004caf1100e87825310600000074af11007c1cd4006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000120000000c00000001000000180000000c0000000000000254000000540000000000000000000000350000006f00000001000000dd898740397687400000000057000000010000004c000000040000000000000000000000e40d0000ee02000050000000200056003600000046000000280000001c0000004744494302000000ffffffffffffffffe30d0000f0020000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0272001a02040000002e0118001c000000fb02f2ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010000040000002d010000040000002d0100000400000002010100050000000902000000020d000000320a0d00000001000400000000001a027200200d08001c000000fb020200010000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010100040000002d010100030000000000
Рисунок 10 – Граф состояний исследуемой СМО
Поскольку все состояния являются сообщающимися и существенными, то существует предельное распределение вероятностей состояний. В стационарных условиях поток, входящий в данное состояние должен быть равен потоку, выходящему из данного состояния.
>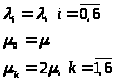 > (1)
> (1)
Для состояния S>0>:
>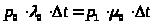 >
>
Следовательно:
>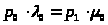 >
>
Для состояния S>1>:
>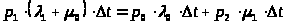 >
>
Следовательно:
>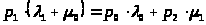 >
>
С учетом того, что
>
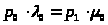 >:
>:
>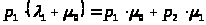 >
>
>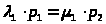 >
>
Аналогично получаем уравнения для остальных состояний системы. В результате получим систему уравнений:
>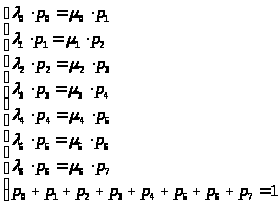 >
>
Решение этой системы будет иметь вид:
>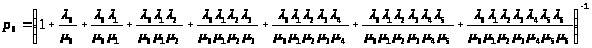 >
>
>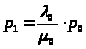 >;
>
>;
>
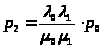 >;
>
>;
>
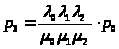 >;
>
>;
>
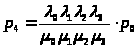 >;
>
>;
>
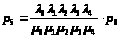 >;
>;
>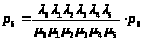 >;
>
>;
>
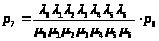 >.
>.
Или, с учетом (1):
>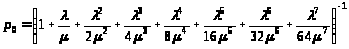 >
>
>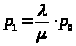 >;
>
>;
>
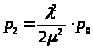 >;
>
>;
>
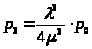 >;
>
>;
>
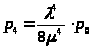 >;
>
>;
>
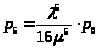 >;
>
>;
>
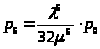 >;
>;
>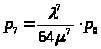 >.
>.
Коэффициент загруженности СМО:
>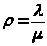 >
>
>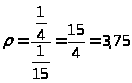 >
>
С учетом этого предельные вероятности перепишем в виде:
>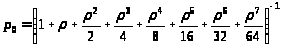 >
>
>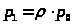 >
>
>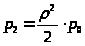 >
>
>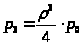 >
>
>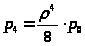 >
>
>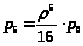 >
>
>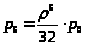 >
>
>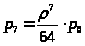 >
>
>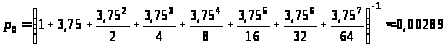 >
>
>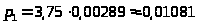 >
>
>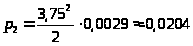 >
>
> >
>
>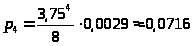 >
>
>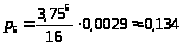 >
>
>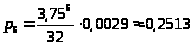 >
>
>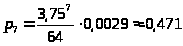 >
>
Наивероятнейшее состояние – оба канала СМО заняты и заняты все места в очереди.
Вероятность образования очереди:
>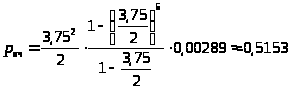 >
>
Отказ в обслуживании заявки происходит, когда все m мест в очереди заняты, т.е.:
> >
>
Относительная пропускная способность равна:
>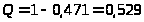 >
>
Вероятность того, что вновь поступившая заявка будет обслужена, равна 0,529
Абсолютная пропускная способность:
>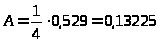 >
>
СМО обслуживает в среднем 0,13225 заявок в минуту.
Среднее число заявок, находящихся в очереди:
>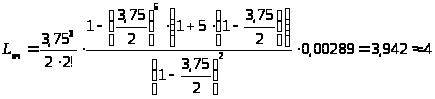 >
>
Среднее число заявок в очереди близко к максимальной длине очереди.
Среднее число заявок, обслуживаемых в СМО, может быть записано в виде:
>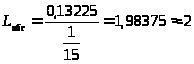 >
>
В среднем все каналы СМО постоянно заняты.
Среднее число заявок, находящихся в СМО:
>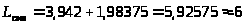 >
>
Для открытых СМО справедливы формулы Литтла:
Среднее время пребывания заявки с СМО:
>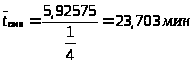 >
>
Среднее время пребывания заявки в очереди:
>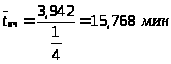 >
>
7.3 Выводы о работе исследуемой СМО
Наиболее вероятное состояние данной СМО – занятость всех каналов и мест в очереди. Приблизительно половина всех поступающих заявок покидают СМО необслуженными. Приблизительно 66,5% времени ожидания приходиться на ожидание в очереди. Оба канала постоянно заняты. Все это говорит о том, что в целом данная схема СМО неудовлетворительна.
Чтобы снизить загрузку каналов, сократить время ожидания в очереди и снизить вероятность отказа необходимо увеличить число каналов и ввести систему приоритетов для заявок. Число каналов целесообразно увеличить до 4. Также необходимо сменить дисциплину обслуживания с FIFO на систему с приоритетами. Все заявки теперь будут иметь принадлежность к одному из двух приоритетных классов. Заявки I класса имеют относительный приоритет по отношению к заявкам II класса. Для расчета основных показателей этой видоизмененной СМО целесообразно применить какой-либо из методов имитационного моделирования. Была написана программа на языке Visual Basic, реализующая метод Монте-Карло.
8 Исследование видоизмененной СМО
Пользователю при
работе с программой необходимо задать
основные параметры СМО, такие как
интенсивности потоков, количество
каналов, приоритетных классов, мест в
очереди (если количество мест в очереди
равно нулю, то СМО с отказами), а также
временной интервал модуляции и количество
испытаний. Программа преобразовывает
сгенерированные случайные числа по
формуле (34), таким образом, пользователь
получает последовательность временных
интервалов >
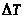 >,
распределенных показательно. Затем
отбирается заявка с минимальным >
>,
распределенных показательно. Затем
отбирается заявка с минимальным >
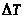 >,
и ставится в очередь, согласно ее
приоритету. За это же время >
>,
и ставится в очередь, согласно ее
приоритету. За это же время >
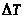 >
происходит перерасчет очереди и каналов.
Затем эта операция повторяется до
окончания времени модуляции, задаваемого
изначально. В теле программы присутствуют
счетчики, на основании показаний которых
и формируются основные показатели СМО.
Если для увеличения точности было задано
несколько испытаний, то в качестве
конечных результатов принимается оценка
за серию опытов. Программа получилась
достаточно универсальной, с ее помощью
могут быть исследованы СМО с любым
количеством приоритетных классов, либо
вообще без приоритетов. Для проверки
корректности работы алгоритма, в него
были введены исходные данные классической
СМО, исследуемой в разделе 7. Программа
смоделировала результат близкий к тому,
который был получен с помощью методов
теории массового обслуживания (см.
приложение Б). Погрешность, возникшая
в ходе имитационного моделирования,
может быть объяснена тем, что проведено
недостаточное количество испытаний.
Результаты, полученные с помощью
программы для СМО с двумя приоритетными
классами и увеличенным числом каналов,
показывают целесообразность этих
изменений (см. приложение В). Высший
приоритет был присвоен более «быстрым»
заявкам, что позволяет быстро обследовать
короткие задания. Сокращается средняя
длина очереди в системе, а соответственно
минимизируется средство для организации
очереди. В качестве основного недостатка
данной организации можно выделить то,
что «долгие» заявки находятся в очереди
длительно время или вообще получают
отказ. Введенные приоритеты могут быть
переназначены после оценки полезности
того или иного типа заявок для СМО.
>
происходит перерасчет очереди и каналов.
Затем эта операция повторяется до
окончания времени модуляции, задаваемого
изначально. В теле программы присутствуют
счетчики, на основании показаний которых
и формируются основные показатели СМО.
Если для увеличения точности было задано
несколько испытаний, то в качестве
конечных результатов принимается оценка
за серию опытов. Программа получилась
достаточно универсальной, с ее помощью
могут быть исследованы СМО с любым
количеством приоритетных классов, либо
вообще без приоритетов. Для проверки
корректности работы алгоритма, в него
были введены исходные данные классической
СМО, исследуемой в разделе 7. Программа
смоделировала результат близкий к тому,
который был получен с помощью методов
теории массового обслуживания (см.
приложение Б). Погрешность, возникшая
в ходе имитационного моделирования,
может быть объяснена тем, что проведено
недостаточное количество испытаний.
Результаты, полученные с помощью
программы для СМО с двумя приоритетными
классами и увеличенным числом каналов,
показывают целесообразность этих
изменений (см. приложение В). Высший
приоритет был присвоен более «быстрым»
заявкам, что позволяет быстро обследовать
короткие задания. Сокращается средняя
длина очереди в системе, а соответственно
минимизируется средство для организации
очереди. В качестве основного недостатка
данной организации можно выделить то,
что «долгие» заявки находятся в очереди
длительно время или вообще получают
отказ. Введенные приоритеты могут быть
переназначены после оценки полезности
того или иного типа заявок для СМО.
Заключение
В данной работе была исследована двухканальная СМО методами теории массового обслуживания, рассчитаны основные показатели, характеризующие ее работу. Был сделан вывод о том, что данный режим работы СМО не является оптимальным и были предложены методы, снижающие загруженность и повышающие пропускную способность системы. Для проверки этих методов была создана программа, моделирующая метод Монте-Карло, с помощью которой были подтверждены результаты вычислений для исходной модели СМО, а также рассчитаны основные показатели для видоизмененной. Погрешность алгоритма может быть оценена и снижена путем увеличения количества испытаний. Универсальность программы позволяет использовать ее при исследовании различных СМО, в том числе и классических.
Список использованных источников
1 Вентцель, Е.С. Исследование операций / Е.С. Вентцель. - М.: «Советское радио», 1972. - 552 с.
2 Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. - М.: «Высшая школа», 2003. - 479 с.
3 Лаврусь, О.Е. Теория массового обслуживания. Методические указания/ О.Е. Лаврусь, Ф.С. Миронов. - Самара: СамГАПС, 2002.- 38 с.
4 Саакян, Г.Р. Теория массового обслуживания: лекции / Г.Р. Саакян. - Шахты: ЮРГУЭС, 2006. - 27 с.
5 Авсиевич, А.В. Теория массового обслуживания. Потоки требований, системы массового обслуживания / А.В. Авсиевич, Е.Н. Авсиевич. - Самара: СамГАПС, 2004. - 24 с.
6 Черненко, В.Д. Высшая математика в примерах и задачах. В 3. т. Т. 3/ В.Д. Черненко. - Санкт – Петербург: Политехника, 2003. - 476 с.
7 Клейнрок, Л. Теория массового обслуживания / Л. Клейнрок. Пер.с англ./ Пер. И.И. Грушко; под ред. В.И. Нейман. - М.: Машиностроение, 1979. - 432 с.
8 Олзоева, С.И. Моделирование и расчет распределенных информационных систем. Учебное пособие / С.И. Олзоева. - Улан-Удэ: ВСГТУ, 2004. - 66 с.
9 Соболь, И.М. Метод Монте-Карло / И.М. Соболь. - М.: «Наука», 1968. - 64 с.
 >
>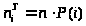 >
>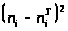 >
>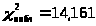 >
>