Кванты излучения и переходы. Уровни энергии и спектральные переходы в атоме водорода
- 1 -
Кванты излучения и переходы.
Уровни энергии и спектральные переходы в атоме водорода
Содержание:
Спектральные характеристики света.
Уровни и спектральные переходы в атоме водорода.
Спектры уровней и матрицы переходов.
Квантовая механика изучает объекты с размерами от 10-710-8 см до
10-16см.
Её разделы, посвящённые строению вещества:
Квантовая химия, изучает электронное строение атомно-молекулярных, в том числе и полимерных систем, таких, как кристаллы и макромолекулы, в том числе и биологических макромолекул. Её традиционные интересы обычно лежат в нерелятивистской области, хотя по необходимости и всё чаще она прибегает и к релятивистским уточнениям.
Ядерная (субатомная) физика изучает объекты с размерами от размера атомного ядра и менее, т.е. 10-13 до 10-16 см. До расстояний порядка 10-16 см удаётся экспериментально наблюдать признаки сложной структуры многих субатомных частиц, но на меньших расстояниях признаки сложной структуры частиц в настоящее время не установлены.
В последние годы возникал наноэлектроника. Она занимается объектами, размеры которых порядка 10-7 см (10-9 м). На рубеже 20-21 веков это область новейших фундаментально-научных и инженерно-технологических изысканий. К её пределам вплотную подошло направленное конструирование микроэлементов вычислительной техники (чипов).
Основные типы взаимодействий в природе
В исследованной области энергий, которая соответствует предельному пространственному разрешению порядка от 10-15 до 10-16 см проявляются четыре типа взаимодействий:
- сильное проявляется на расстояниях порядка размера ядра от 10-13см и менее. Причиной сильного взаимодействия являются ядерные силы, которые в ядре действуют между нейтроном и протоном и обеспечивает стабильность ядра. В нём участвует большинство известных в настоящее время частиц,
- электромагнитное, в котором участвуют все электрически заряженные (и некоторые нейтральные) частицы; на расстояниях порядка размера ядра оно слабее сильного взаимодействия. Именно с электромагнитными взаимодействиями связано и существование, и физические свойства атомно-молекулярных систем,
- слабое проявляется на расстояниях, не превышающих 10-16 см; оно является причиной распада некоторых видов субатомных частиц,
(в настоящее время установлено, что на расстояниях менее 10-16 см проявляется единое электрослабое взаимодействие),
- гравитационное, которое действует на всех расстояниях, но по сравнению с прочими на соответствующих им расстояниях оно исчезающе мало. Так его величина на 36 десятичных порядков меньше, чем у электростатического взаимодействия, скажем, двух протонов. Его роль важна в макромире, особенно в космических масштабах.
Частицы и волны в классической механике
Классической механикой принято называть раздел физики, изучающий законы движения макроскопических тел. В классической механике принято различать:
движения локализованных масс. Их принято называть корпускулярными системами. Поступательное движение отдельной корпускулы с очень большой точностью можно описать на основе механики материальной точки, расположенной в центре масс.
движения сплошных сред возникают при возмущении пространственно непрерывно распределённой среды. Такие движения имеют периодический волновой характер.
Таким образом, корпускула это пространственно локализованная масса (в пределе доходящая до материальной точки), а волна это движение непрерывной среды с признаками периодичности в пространстве и во времени.
Корпускулярно-волновая природа излучения
Волновые свойства света были экспериментально установлены ещё в 17-м столетии. О волновой природе света неопровержимо свидетельствуют чисто волновые явления дифракции - огибания небольших пространственных препятствий световой волной, а далее интерференции – возникновения пространственно чередующихся областей взаимного усиления (в фазе) и взаимного ослабления (в противофазе) налагающихся когерентных волн, исходящих из двух или нескольких точек пространства (кольца Ньютона, зоны Френеля и т. д.). Механические волны распространяются в сплошной среде, и для световой волны по аналогии также постулировали гипотетическую сплошную среду, которую назвали эфиром.
Во 2-й половине 19 века открыли электромагнитное поле, и стало ясно, что световая волна представляет его колебания, а эфир - не более, чем гипотетическая модель непрерывной среды. Ожидаемые свойства эфира не подтвердились. Оказалось, что оптический видимый диапазон длин волн охватывает лишь очень малую часть огромной шкалы электромагнитного спектра, он в длинноволновой области переходит в радиочастотный диапазон, а в коротковолновой – в рентгеновское, а далее в -излучение.
Волновая теория, вытекающая из электродинамики, до мельчайших особенностей объяснила все геометрические закономерности распространения излучения в пространстве, и в терминах механики это означает, что кинематика света подчиняется волновым законам.
На рубеже 19-20 веков были экспериментально открыты факты, которые не укладывались в волновую концепцию света. Все такие явления затрагивают взаимодействие излучения и вещества – законы поглощения и испускания (абсорбции и эмиссии) света. Рентгеновское излучение, имеет ту же природу, что и видимый свет. Это обычное электромагнитное поле, но отличается от оптического диапазона очень малыми длинами волн, наименьшими из известных в то время. При описании свойств коротковолнового излучения не удалось ограничиться лишь волновыми законами, и пришлось ввести корпускулярные представления о структуре электромагнитного поля.
Среди первичных явлений, необъяснимых без корпускулярной модели оказались фотоэффект, термодинамика равновесного излучения абсолютно чёрным телом, и рассеяние рентгеновского излучения веществом (эффект Комптона). Для количественного описания экспериментальных фактов потребовалось ввести представления об элементарных частицах электромагнитного излучения – фотонах, а переносимые ими порции энергии были названы квантами. Особенность фотонов состоит в том, что их масса покоя нулевая.
Возникла, как показалось на первый взгляд, противоречивая ситуация.
С одной стороны движущееся электромагнитное поле - непрерывная среда, а с другой структурно-дискретное образование – поток частиц-фотонов.
Этот раздел предназначен для вводных упражнений в студенческой аудитории. Его цель – простейшее обсуждение комбинационного принципа, связывающего энергетические уровни простейшего атома с частотами, волновыми числами, энергиями спектральных переходов.
Здесь приведены элементарные сведения о характеристиках электромагнитного излучения, таких как длина волны, волновое число, частота и энергия спектрального перехода, области электромагнитного излучения и диапазоны спектральных методов, используя формулу Планка-Эйнштейна ( =h).
Полезно отметить, что в течение первых десятилетий 20-го века поглощение и эмиссия и рассеяние излучения наблюдались в виде однофотонных процессов. Позднее с открытием нелинейной оптики и созданием мощных лазерных источников излучения были открыты многофотонные процессы.
3.1. Энергия поглощаемого или испускаемого фотона - кванта электромагнитного поля прямо пропорциональна частоте излучения , обратно пропорциональна длине волны , прямо пропорциональна волновому числу и определяется известной формулой Планка:
(3.1)
Это соотношение позволяет для отсчёта энергии использовать и единицы измерения частоты (1 герц = с-1 или кратные ему величины 1 килогерц =103 герц, или1ме-гагерц =106 герц, или 1 гигагагерц =109 герц и т.д.), и единицы измерения волнового числа (чаще всего обратные сантиметры [] см-1). Эти разные шкалы отсчёта энергии используются в различных областях экспериментальной спектроскопии.
Так, например, в оптической спектроскопии, изучающей электронные переходы в атомах и молекулах, используются обратные сантиметры (см-1), в радиоспектроскопии, изучающей процессы переориентации векторов магнитных моментов электронов или ядер (спиновых векторов ядер или электронов), обычно применяет единицы частоты - мегагерцы или гигагерцы (мГц, гГц,). В спектроскопии высоких энергий, использующей рентгеновское или гамма-излучение, обычной единицей является электроновольт (эВ).
3.2. Уровни квантовых
систем являются элементами одномерных
массивов - энергетических спектров
и могут быть пронумерованы каким-либо
дискретным числовым множеством, чаще
всего
,
где квантор V означает «или»
.
(3.2)
Числа-номера уровней
называются квантовыми числами. Они
образуют массивы. Дис-танции между
уровнями
образуют
уже двумерные упорядоченные массивы -
матрицы:
.
(3.3)
Каждой паре уровней
соответствует два перехода. Энергии
поглощаемого и испускаемого квантов
(поглощаемого или испускаемого фотона)
почти одинаковы, и эту пару переходов
удобно изобразить символом
или можно просто парой индексов, которые
в зависимости от направления перехода
чередуются как nm (переход n
m) или как mn (переход m
n).
3.3. Поглощение или испускание фотона системой по закону сохранения энергии связано с её переходами вдоль лесенки дискретных уровней энергии, и поэтому каждому из возможных переходов отвечает своя частота или своё волновое число. Частоты, волновые числа и длины волн, порождаемые этими квантовыми переходами, характеризуют электромагнитный спектр системы. Они также образуют матрицы и могут быть пронумерованы индексами:
.(3.4)
Упорядоченная сводка характеристик системы, которые зависят от пар уровней, всегда представляет собой двумерную матрицу. Её структура проста и совпадает с принципом нумерации её элементов :
По такой схеме получается спектр частот электронных переходов в атомарном водороде.
3.4 Атом водорода, уровни и переходы, частоты и спектральные серии
(Упражнения для практического занятия.)
3.4.1. Уровни энергии.
Выше была выведена формула Бора для уровней энергии водородоподобного иона. Это электронные уровни. Состояния одной частицы принято называть орбиталями, поэтому эти уровни называют также орбитальными:
(3.5)
Z -порядковый номер элемента. –приведённая масса (e) .
Орбитальные уровни дискретны, и это выражается в том, что в формулу входит переменная, у которой просто не бывает нецелочисленных значений. Это квантовое число n.
3.4.2. Универсальные мировые постоянные равны:
3.4.3. Формула Бора может быть записана в очень простом виде. (Z=1).
Для этого универсальные константы объединяются в один множитель, получая:
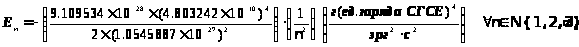
Спектр энергетических уровней приобретает вид:
Упорядочим размерности, а именно:
,
поскольку
Используя приведённую массу, находим A=2.1787221 эргсм.
3.4.4. Спектральные переходы характеризуются волновыми числами (или частотами):
.(3.6)
Наиболее просто это выглядит как
(3.7)
3.4.5. Постоянная Ридберга это коэффициент R. Её значение:
В спектре атомарного водорода (рис.) возникают следующие серии
Формуле (3.7) можно придать очень простой матричный вид
,
где
,
(3.8)
3.4.6. Диагональные
матричные элементы нулевые и не имеют
смысла. Переходам отвечают лишь
недиагональные матричные элементы
;
все они содержатся в одной из двух
треугольных субматриц, лежащих одна -
над-, а вторая - под нулевой диагональю,
и
.
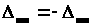Элементы положительной матрицы представляют собой рациональные дроби, равные:
n 1 2 3 4 5 ... серия m
Умножением этих матричных элементов на константу Ридберга, получается матрица волновых чисел переходов в единицах волнового числа (см-1):
3.4.7. Спектральные серии представляют собою строки в этой матрице.
Далее можно рассчитать и матрицу длин волн в нанометрах, учитывая, что 1см =107 нм:
3.4.8. Область цветного зрения человека охватывает лишь очень малый диапазон шкалы электромагнитного спектра (~ 400-700 нм). Из пяти приведенных серий спектральных линий в видимый интервал длин волн попадают лишь линии серии Бальмера. Полезно сравнить результаты теоретического расчёта с экспериментальными данными:
У водородоподобного иона (катиона с зарядом, равным Z-1) уровни энергии расположены в Z2 раз реже, чем у атома H и, соответственно, величины сдвигов между его уровнями во столько же раз больше.
-
Эксперимент (нм)
Теория (нм)
Серия
Спектральных линий
1-я
линия
2-я
линия
Начало
контину-ума
n
Уровни АО,
см-1 (Термы)
(ионизация)Лаймана
121.567
102.58
91.17
1
109677.6
91.176
Бальмера
656.274
486.13
364.79
2
27419.4
364.768
Пашена
1875.077
1281.81
820.58
3
12186.4
820.587
Брэккета
4050.000
2630.00
1459.0
4
6854.8
1458.821
Пфунда
7400.000
4600.00
2280.0
5
4387.1
2279.408