Исследование цепи переменного тока

Лабораторная работа

ИССЛЕДОВАНИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА


Цель работы:

Изучение явления резонанса в цепи переменного тока. Проверка закона Ома для цепи переменного тока.

Оборудование: стенд для исследования явлений в цепи переменного тока, генератор переменного тока ГЗ –109 (генератор звуковой), вырабатывающий переменный ток с частотой 20 – 20 000 Гц, т. е. в «звуковом» интервале частот, магазин сопротивлений, мультиметр.

Незатухающие вынужденные электрические колебания обычно называют переменным током. Частота переменного тока f – это число колебаний в 1 секунду. Частота 50 Гц принята для промышленного тока во многих странах мира. С помощью генераторов переменного тока можно получать переменный ток любой частоты. При этом напряжение на выходе генератора обычно меняется по гармоническому закону

, (1)

где =2f - циклическая частота, f - линейная частота, U>m> – амплитуда (максимальное значение) напряжения.

Если источник переменного напряжения (генератор) с частотой подключить к электрической цепи, то в ней возникнут колебания силы тока той же частоты. Но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. В общем случае мгновенное значение силы тока i определяется по формуле

, (2)

где - разность (сдвиг) фаз между колебаниями тока и напряжения, I>m> – амплитуда силы тока.

  • В проводнике с активным сопротивлением (резисторе) колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:

, (3)

где R – (активное) сопротивление резистора.

  • В катушке индуктивности колебания силы тока отстают от колебаний напряжения на угол =/2. Амплитуда силы тока в катушке равна

.

Величину X>L>> >=L = 2fL (4)

называют индуктивным сопротивлением.

  • На конденсаторе колебания силы тока опережают колебания напряжение на угол =/2. Амплитуда силы тока равна:

.

Величину (5)

называют емкостным сопротивлением.

Рассмотрим электрическую цепь (рис. 1), состоящий из соединенных последовательно резистора R, конденсатора С и катушки индуктивности L. Эта цепь является колебательным контуром, в которой возможны собственные электрические колебания с частотой

(6)

Если к концам этой цепи приложено переменное напряжение, изменяющееся по закону (1), то в ней возникнут вынужденные электрические колебания с частотой . Сила этого переменного тока будет определяться по формуле (2), причем для нахождения амплитуды и фазы тока необходимо учесть влияние всех элементов цепи: R, L, С. Лучше всего это можно сделать с помощью векторной диаграммы (треугольника сопротивлений) (рис. 2). Из рисунка видно, что полное сопротивление цепи равно:

, (7)

а сдвиг фаз между током и напряжением

. (8)

Разность X = (X>L> - X>C>) называется реактивным сопротивлением цепи.

Соотношение

(9)

называют законом Ома для цепи переменного тока (по аналогии с законом Ома для постоянного тока I = U/R).

Обычные электроизмерительные приборы для переменного тока позволяют измерять эффективные (действующие) значения силы тока и напряжения, которые связаны с амплитудными значениями:

. (10)

Очевидно, что вид закона Ома для цепи переменного тока не меняется, если вместо амплитудных использовать эффективные значения силы тока и напряжения.

Как известно, резкое увеличение амплитуды колебаний колебательной системы при совпадении частоты вынуждающих колебаний с частотой собственных колебаний системы называется резонансом.

Сила тока в рассматриваемой цепи зависит как от величин R, L, C, так и от частоты вынуждающих колебаний. Если менять частоту переменного тока, подводимого к рассматриваемой цепи, то при определенной частоте индуктивное сопротивление X>L> становится равным емкостному сопротивлению X>C>

(11)

При этом полное сопротивление цепи становится минимальным и равным активному сопротивлению цепи Z =R. Сила тока достигает максимального значения - наступает резонанс, причем резонансная частота совпадает с частотой собственных колебаний контура

(12)

При последовательном соединении элементом цепи (как в данном случае) при резонансе падение напряжения на конденсаторе и катушке индуктивности становятся одинаковыми по величине – резонанс напряжений

, (13)

причем их величины могут значительно превышать приложенное напряжение.

«Острота» резонансной кривой характеризуется ее относительной полушириной:

, (14)

где f=(f>2> –f>1>)) – разность значений частоты, соответствующих . Эта величина Q называется еще добротностью колебательного контура (колебательной системы). Можно показать, что добротность колебательного контура определяется его параметрами:

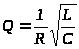(15)

Добротность показывает, во сколько раз падение напряжения на конденсаторе и катушке при резонансе больше, чем приложенное напряжение

(16)

На рисунке 3 показано семейство резонансных кривых при различных значениях активного сопротивления цепи - чем больше активное сопротивление контура, тем менее выражен резонанс.

Выполнение эксперимента

В работе для измерения различных характеристик цепи используется универсальный измерительный прибор – мультиметр. Положение переключателя прибора определяет характер измеряемой величины: сопротивление – «» (пределы 0-200 Ом, 0,2-2 kОм, и т.д.); постоянное напряжение «V-» (пределы 0-200мВ, 0,2-2В и т.д.); переменное напряжение – «V» (пределы 0-2В, 2-20В и т.д.); сила переменного тока – «А» (пределы 0-20мА, 20-200мА и т.д.), сила постоянного тока «А-» (пределы 0-20мА, 20-200 мА и т.д.). Один из щупов постоянно подключен к клемме «СОМ» мультиметра; второй щуп при измерении напряжения и сопротивления подключается к клемме «V/,» а при измерении силы постоянного и переменного тока до 200 мА – к клемме «mA». Следует быть очень внимательным при работе с мультиметром.

В эксперименте используется стенд, собранный по схеме рис. 1. К соответствующим клеммам стенда подключается генератор синусоидальных колебаний, электроизмерительные приборы и магазин сопротивлений, играющий роль активного сопротивления. Параметры входящих в цепь элементов указаны на стенде.

У генератора используется «Выход 2», 5 Ом. При этом собственное сопротивление генератора, как источника тока, оказывается гораздо меньше, чем сопротивление исследуемой цепи, и может не учитываться при расчетах. Выходное напряжение регулируется ручкой «Напряжение – Плавно». Не следует работать в режиме, при котором стрелка индикаторного вольтметра, установленного на генераторе, «зашкалевает», так как при этом может происходить искажение формы выходного сигнала (отклонение сигнала от синусоидальной формы). Частота генерируемого переменного тока регулируется с помощью лимба и ступенчатого переключателя.

Задание 1. Предварительные расчеты и измерения

1. На стенде указаны приблизительные значения емкости установленного конденсатора и индуктивность катушки. Рассчитайте с помощью формулы (12) приблизительное значение резонансной частоты f>рез>> >(записать в отчет). Это дает возможность определиться с областью частот, в которой предстоит делать измерения.

2. Катушка индуктивности, установленная на стенде, имеет значительное активное сопротивление, которое следует учитывать в дальнейших измерениях. Поэтому с помощью мультиметра (переключатель «», 2k – 0,2-2 кОм, щупы подключены к клеммам «COM», «V/») измерьте и запишите в отчет величину активного сопротивления катушки R>L>. Щупы подключаются к клеммам «С>1>, С>2>» стенда.

3. Конденсатор, установленный на стенде, не является идеальным, т.е. в процессе работы он дает утечки тока через изоляцию обкладок, что эквивалентно включению параллельно конденсатору некоторого сопротивления. Однако это явление мы не будем учитывать в дальнейшем, так как его влияние на опыт не велико.

4. Для наблюдения явления резонанса можно следить за изменением в зависимости от частоты: силы тока в цепи, напряжения на катушке или напряжения на конденсаторе. В данном опыте рекомендуется снять зависимость силы переменного тока от частоты I = f(), для чего щупы мультиметра (щупы – «СОМ», «mA», переключатель – «А», 20m,

0-20мА) подключаются к клеммам «А >1, >А>2>» стенда.

5. Включите генератор и дайте ему прогреться несколько минут.

6. Особо следует определить точное значение резонансной частоты. Для этого надо, медленно вращая ручку регулировки частоты в диапазоне (f>рез> 50 Гц) и внимательно наблюдая за показаниями амперметра, «поймать» частоту, при которой сила тока в цепи принимает максимальное значение. Значение резонансной частоты заносится в отчет. Опыт лучше проводить, когда на магазине сопротивлений установлено нулевое значение.

7. Находясь на резонансной частоте, измерьте падение напряжения на конденсаторе

U>C>>РЕЗ> (клеммы «В>1>, В>2>» стенда) и катушке индуктивности U>LРЕЗ>. (клеммы «С>1>, С>2>» стенда). Мультиметр – щупы «COM», «V/», переключатель «V», 20V). Так как при этом измерении амперметр будет выведен из цепи, цепь окажется разорванной. Чтобы ее замкнуть, перемкните клеммы «А>1>, А>2>» стенда перемычкой.

В идеальном случае согласно теории резонанса для цепи с «сосредоточенными» параметрами U>LРЕЗ>. = U>C>>РЕЗ>. Если это не наблюдается, то объясните причины расхождения.

Задание 2. Снятие резонансных кривых.

1. Первый опыт можно провести при нулевом сопротивлении магазина. При этом полное активное сопротивление контура равно активному сопротивлению катушки R = R>L>.

2. Снятие резонансных кривых желательно провести в диапазоне частот: (f>РЕЗ> – 200)Гц – (f>РЕЗ> + 200)Гц с шагом приблизительно 20 Гц.

3. Подключите мультиметр к клеммам «А>1>, А>2>» - п. 4 задания 1. Запишите в таблицу 1 отчета значения силы тока при различных частотах.

4. Снимите еще две резонансные кривые при больших значениях активного сопротивления контура. Второй и третий опыт проведите, введя в контур с помощью магазина сопротивлений дополнительное активное сопротивление, так что R = R>L>+R>M>, где R>M> – сопротивление, устанавливаемое на магазине сопротивлений (например, 100 Ом, 200 Ом).

5. Постройте (на миллиметровой бумаге – формат А4) на одном графике три резонансные кривые. Отметьте резонансную частоту (рис. 3).

6. Отметьте на графике силу тока в меньшее, чем резонансное значение в каждом из опытов. Измерьте ширины f резонансных кривых на этих уровнях рассчитайте по формуле (14) величину добротности контура в трех случаях. Исходя из параметров контура по формуле (15) вычислите добротности контура в трех случаях. В выводе сравните измеренные и вычисленные добротности в каждом случае.

7. Сделайте вывод о влиянии активного сопротивления на вид резонансной кривой и добротность контура.

Задание 3. Проверка закона Ома для цепи переменного тока

Цель этого задания сравнить измеренное и вычисленное значение силы тока в цепи переменного тока.

1. Проверку желательно проводить на частоте, значительно (на 100-200 Гц) отличающееся от резонансной частоты, например на частоте 300 Гц.

2. По формулам (4), (5) вычислите величины индуктивного X>L> и емкостного X>C> сопротивления на выбранной частоте. При этом используйте значения емкости конденсатора и индуктивности катушки, указанные на стенде. Вычислите величину реактивного сопротивления X = X>L> - X>C>> >.

4. Установите на магазине сопротивлений дополнительное активное сопротивление 100 – 200 Ом. Запишите полное активное сопротивление контура.

3. На миллиметровке (той же, что и для резонансных кривых) постройте треугольник сопротивлений (рис. 2). Можно выбрать масштаб 1 см = 100 Ом. Определите полное сопротивление цепи Z. Определите tg и угол сдвига фаз между током и напряжением.

5. Установите выбранную частоту. Измерьте подаваемое на цепь напряжение U (клеммы «D>1>, D>2>» стенда; мультиметр – щупы «COM», «V/», переключатель «V», 20V).

5. Вычислите по закону Ома (10) предполагаемую силу тока I в цепи при данных условиях

6. Подключите к стенду амперметр - клеммы «А >1, >А>2>» стенда (мультиметр, щупы – «СОМ», «mA», переключатель – «А», 20m). Измерьте силу тока в контуре.

7. В выводе сравните между собой вычисленное и измеренное значение силы тока и сделайте вывод о выполнении закона Ома.

Отчет по лабораторной работе № 1

Исследование цепи переменного тока.

выполненной учащим…… школы «Поиск»

……………………………………………………………………………………

«…..»……….. 200….г

Задание 1. Предварительные расчеты и измерения

Емкость конденсатора: С =……… мкФ =……… 10-6 Ф

Индуктивность катушки: L =……… мГн =…………………… Гн

Активное сопротивление катушки индуктивности: R>L> = ……… Ом

Расчетная резонансная частота: f>рез> = …………Гц

Измеренная резонансная частота: f>рез> = …………Гц

Падение напряжение на конденсаторе при резонансе: U>C>>РЕЗ>. = …… В

Падение напряжение на катушке индуктивности при резонансе: U>LРЕЗ>. = ……В

Выводы:

Задание 2. Снятие резонансных кривых

Выбранный диапазон частот ………………………………………….

Таблица 1

№ п/п

f, Гц

I, мА

I, мА

I, мА

Активное сопр-е контура

R>1> =……… Ом

R>2> = ……… Ом

R>3> = ………Ом

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

График – миллиметровка А4. Подписать: «Резонанс напряжений – последовательный резонанс».

Обозначить оси. Показать резонансную частоту. Указать R>1>, R>2>, R>3>.


Таблица 2

№п/п

Измеренная добротность контура

Вычисленная добротность контура

f>рез>, Гц

f, Гц

Q>изм>

R, Ом

Q>выч>

1

2

3

Выводы:

Задание 4. Проверка закона Ома для цепи переменного тока

Частота: f =……… Гц

Индуктивное сопротивление: X>L> =……… Ом

Емкостное сопротивление: X>C> =………Ом

Реактивное сопротивление контура: X = X>L> - X>C>> >.

Активное сопротивление катушки индуктивности: R>L> =……… Ом

Сопротивление магазина сопротивлений: R>м> =……… Ом

Полное активное сопротивление контура: R = ……… Ом

Полное сопротивление контура: Z =……… Ом

Напряжение, подаваемое на контур: U = ……… В

Расчетная сила тока в цепи: I =……… мА

Измеренная сила тока в цепи: I = ……… мА

tg = …… ; =……….