Модель парной регрессии

Содержание

ТЕМА 1. Выборка и генеральная совокупность

Задача 1

ТЕМА 2. Модель парной регрессии

Задача 12

ТЕМА 3. Модель множественной регрессии

Задача 13

ТЕМА 4. Нестационарные временные ряды

Задача 23

ТЕМА 1. Выборка и генеральная совокупность

Задача 1

1. Найдите среднее число государственных вузов в России, если данные их статистического учета с 1994 по 2000г таковы

Год

1994

1995

1996

1997

1998

1999

2000

Число государственных вузов

548

553

569

573

578

582

584

2. Найдите вариацию числа государственных вузов в России за 1994 2000гг

Решение

Определим выборочное среднее государственных вузов в России, по зависимости учитывая, что n=7.

Найдем вариацию числа государственных вузов в России за 1994-2000г по формуле:

Таким образом, среднее число государственных вузов в России составляет 570 шт, а вариация 169.

ТЕМА 2. Модель парной регрессии

Задача 12

1. Предварительно вычисленная ковариация двух рядов составляет -4.32, а вариация ряда занятых в экономике равна 7,24. Средние выборочные равняются 68,5 и 5,87 соответственно. Оцените параметры линейного уравнения парной регрессии .

Решение

Оценим параметры линейного уравнения парной регрессии

Зная выборочные ковариацию и вариацию, вычислим параметр b по формуле (4)

а параметр a по зависимости

На основании полученных данных уравнение парной регрессии примет вид

Определим объясненную сумму квадратов отклонений ESS по формуле (8)

ТЕМА 3. Модель множественной регрессии

Задача 13

  1. В таблице представлены ряды данных по продовольственным ресурсам (производству и импорту ) и личному потреблению картофеля y (млн. тонн) за 9 лет

Год

1990

1991

1992

1993

1994

1995

1996

1997

1998

30.8

34.3

38.3

37.7

33.8

39.9

38.7

37

31.4

1.1

1.2

0.4

0.2

0.1

0.1

0.1

0.2

0.33

y

15.7

16.7

17.5

18.8

18

18.3

18.5

19.1

18

Рассчитать вариации и попарные ковариации для этих рядов.

  1. По данным таблицы построить уравнение регрессии, приняв личное потребление картофеля за зависимую переменную, а производство и импорт - за объясняющие. Рассчитать коэффициенты при объясняющих переменных.

  2. Для регрессии, описывающей линейную зависимость потребления картофеля от производства и импорта , определить свободный коэффициент a.

  3. Рассчитать значения личного потребления y картофеля, используя полученное в задаче уравнение регрессии.

  4. Рассчитать общую, объясненную и необъясненную сумму квадратов отклонений для рассчитанной ранее регрессии для личного потребления y картофеля.

  5. Используя полученные в предыдущем пункте TSS и ESS, рассчитать коэффициент детерминации для регрессии по картофелю.

Решение

Определим выборочные средние , и по формуле (1) при числе наблюдений: n=9

млн. т

млн. т

млн. т

Рассчитаем вариации и попарные ковариации для этих рядов. Вариации для рядов объясняющих переменных и можно вычислить по зависимостям (11)

А вариацию зависимой переменной y по зависимости (12)

Попарные ковариации для этих рядов определяются по (13) как

По данным таблицы построим уравнение регрессии

,

Приняв личное потребление фруктов за зависимую переменную, а производство и импорт - за объясняющие, предварительно рассчитав коэффициенты при объясняющих переменных.

Расчет коэффициентов и производим по зависимостям (15) и (16)

Для регрессии, описывающей линейную зависимость потребления фруктов от производства и импорта , определить свободный коэффициент a.

Свободный коэффициент уравнения регрессии вычисляется как

млн. т

Рассчитаем значения личного потребления y фруктов, используя полученное в задаче уравнение регрессии.

Расчет значений по зависимости

сведен в табл.2.

Таблица 2

Год

1990

1991

1992

1993

1994

1995

1996

1997

1998

16.16

16,21

18,04

18,38

18,31

18,73

18,65

18,33

17,68

-

-1,68

-1,63

0,56

0,54

0,47

0,89

0,81

0,49

-0,16

(-)2

2,82

2,66

0,3

0,3

0,2

0,8

0,7

0,24

0,03

y>i>

15,7

16,7

17,5

18,8

18

18,3

18,5

19,1

18

(y>i> - )

-2,14

-1,14

-0,34

0,96

0,16

0,46

0,67

1,26

0,16

(y>i> - )2

4,58

1,3

0,12

0,92

0,03

0,21

0,45

1,59

0,03

Рассчитаем общую и объясненную сумму квадратов отклонений для рассчитанной ранее регрессии для личного потребления y фруктов.

Определим объясненную сумму квадратов отклонений ESS по формуле (8)

с помощью результатов, приведенных в табл.2. Тогда получим

Общая сумма квадратов отклонений ТSS находится по зависимости (9)

с использованием данных табл.2. Суммируя результаты, приведенные в последней строке этой таблицы, получим

Используя полученные в предыдущем пункте величины TSS и ESS, рассчитаем коэффициент детерминации для регрессии по фруктам в соответствии с (7) как отношение ESS к TSS

Оценим теперь коэффициент корреляции для фактических y и прогнозных значений . Фактически, коэффициент детерминации равен квадрату выборочной корреляции между y и , т.е.

В соответствии с зависимостью (20) имеем

,

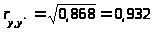Вывод: Полученная величина коэффициента корреляции лежит в диапазоне 0,7-0,9, что указывает на хорошее состояние соответствия уравнения регрессии фактическому изменению величины у.

ТЕМА 4. Нестационарные временные ряды

Задача 23

По данным таблицы в задаче 18, где представлены данные по личным потребительским расходам на газ (млн. долл.) с 1969 по 1983гг. (США), с помощью критерия, основанного на критерии восходящих и нисходящих серий, проверить гипотезу о неизменности среднего значения временного ряда.

  1. В таблице представлены данные по личным потребительским расходам на газ (млн. долл.) с 1969 по 1983гг. (США)

Год

1969

1970

1971

1972

1973

1974

1975

1976

расходы

6200

6300

6400

6600

6400

6500

6600

6700

Год

1977

1978

1979

1980

1981

1982

1983

расходы

6500

6700

6600

6600

6300

6400

6000

Решение

Определяем число наблюдений n=15. Для нахождения медианы производим ранжирование временного ряда, т.е. записываем все значения ряда по порядку от минимального до максимального:

6000,6200,6300,6300,6400,6400,6400,6500,6500,6600,6600,6600,6600,6700,6700.

Поскольку число наблюдений n нечетное, то вычисляем медиану по формуле ( )

Теперь вместо исходного временного ряда, содержащегося в таблице, создаем ряд из плюсов и минусов согласно правилу:

«+» если и «-» если . Члены не учитываются

Ряд, состоящий из плюсов и минусов, имеет вид

«>+>», «+»,«+», «+»,«+»,«+»,«+»,«+»,«+»,«+»,«+»,«+», «+».

Глядя на полученный ряд из плюсов и минусов, определяем общее число непрерывных серий из плюсов и из минусов . В данном случае . Определяем протяженность самой длинной серии .

Проверяем выполнение неравенств

Вывод. Поскольку ни одно из неравенств не выполняется (4<5, а 6>4), то гипотеза о неизменности среднего значения отвергается с вероятностью ошибки от 0,05 до 0,0975.

Список литературы

  1. Эконометрика. Юниты 1,2,3. //Разработка С.Б.Давыдовой. -М.:Современная гуманитарная академия. -2006.

  2. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. М.: Дело. 2001.- 400с.

  3. Афанасьев В.Н., Юзданцев М.М., Гуляева Т.Н. Эконометрика. Учебник. – М.: Финансы и статистика., 2006.

  4. Елисеева Н.Н., Кудряшова С.В., Костеева Т.В. . Эконометрика. Учебник. М.: Финансы и статистика., 2005.-576с.

  5. Бородин С.А. Эконометрика: учебное пособие. – М.: Новое издание, 2001.

  6. Колемаев В.А. Эконометрика. Учебник. – М.: ИНФРА – М, 2005 -160с.