Модель авторегрессии в корреляционной теории
Модель авторегрессии в корреляционной теории
1. Принципы построения модели авторегрессии
В основу модели АР положена корреляция отсчета случайного процесса в текущий момент времени с некоторым конечным или бесконечным числом отсчетов в предыдущие моменты времени. Корреляционные связи позволяют осуществить регрессию текущего отсчета на предшествующие отсчеты.
Такой вид регрессии называется авторегрессией. В уравнении АР текущий отсчет представляется взвешенной суммой предыдущих с некоторыми коэффициентами веса
,
(1)
где
-
коэффициенты АР,
-
некоррелированные случайные отсчеты,
-
порядок модели АР.
Величина
,
(2)
называется
предсказанием случайной величины
.
Разность между текущим значением отсчета
и его предсказанием называется ошибкой
предсказания
.
(3)
Величина
характеризует, по существу, максимальную
точность предсказания текущего отсчета,
а ее статистические свойства определяют
выбор порядка модели АР.
Из (1) видно,
что построение АР модели случайного
процесса сводится к нахождению
коэффициентов АР и определению порядка
.
Умножив правую
и левую части (1) на
,
а затем усреднив, можно получить систему
уравнений
,
,
(4a)
,
(4б)
где
-
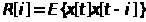значения функции корреляции случайного
процесса
-
дисперсия ошибок предсказания модели
АР,
-
дисперсия случайного процесса
.
Набор уравнений (4а) и (4б) называется
полной системой уравнений Юла – Уокера.
Решением этой системы являются коэффициенты АР и дисперсия ошибок предсказания. При выводе уравнений (4а) было учтено, что
,
,
,
(5a)
,
,
.
(5б)
Соотношения
(5) следуют из некоррелированности ошибок
предсказания
.
Решение системы уравнений (4а) можно
представить в матричном виде
,
(6a)
где
,
,
.
(6б)
Как видно из
(4а), уравнение не изменится, если вместо
использовать нормированные значения
функции корреляции
,
которые называются коэффициентами
корреляции. Очевидно, что при этом
параметры модели АР останутся прежними.
Как следует из (6а, б), для первого порядка модели АР
.
(7)
Для модели АР второго порядка коэффициенты АР равны
,
.
(8)
Отметим важное свойство коэффициентов АР, на котором основано использование моделей предсказания в качестве обеляющих фильтров. Коэффициенты АР, рассчитанные с помощью уравнений Юла-Уокера (4а) минимизируют дисперсию ошибки предсказания
.
(9)
В этом легко
убедиться, продифференцировав (9) по
,>
>и приравняв
производную к нулю. При этом полученная
система уравнений совпадает с (4а).
Достоинством модели АР является ее конструктивность, заключающаяся в возможности синтеза довольно простым образом алгоритмов обработки случайных процессов.
На рис. 1
представлен АР фильтр предсказания
(обеляющий фильтр), алгоритм действия
которого описывается выражением (3). Он
состоит из линий задержки, усилителей
с коэффициентами усиления
,
и
сумматора.
Ошибки предсказания на выходе этого фильтра будут отсчетами белого шума, а точнее некоррелированным процессом. Дисперсия ошибки предсказания на выходе фильтра будет иметь минимальное значение, если коэффициенты АР найдены из уравнения (4а).
Порядок процесса АР определяется с использованием различных критериев, как правило, основанных на минимизации некоторой теоретико-информационной функции. Для определения порядка модели пользуются методами Бартлетта, Акайке, Парзена.
Порядок модели можно находить из условия не убывания дисперсии ошибки предсказания при дальнейшем повышении порядка. Довольно эффективным методом определения порядка модели АР является метод, основанный на проверке близости корреляционной функции случайного процесса на выходе обеляющего АР фильтра к корреляционной функции белого шума.
Рисунок 1. АР фильтр предсказания
Процессы АР можно характеризовать конечным числом значений функции, определяемой корреляционной функцией.
Такая функция
носит название частной автокорреляционной
функции. Ее можно выразить через
коэффициенты АР, порядок которых
изменяется от единицы до
.
Т.к. коэффициент
АР с номером
полагается равным нулю, то процесс АР
можно характеризовать конечным набором
не равных нулю коэффициентов АР, с
номером равным р
для моделей АР с порядками от единицы
до
>
>-
,
.
Поэтому
значения частной автокорреляционной
функции полагаются равными
,
.
Можно показать, что первые три значения
частной автокорреляционной функции
описываются выражениями вида
,
,
.
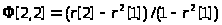(10)
Достоинством частной автокорреляционной функции по сравнению с автокорреляционной функцией является ее конечная длина.
Как показал
Бартлетт, значение частной автокорреляционной
функции можно полагать равным нулю,
если оно меньше
,
где
-
длина реализации, по которой производилась
оценка значений функции корреляции.
Таким образом, по существу, производится
оценка порядка модели АР.
Спектр процесса авторегрессии
Формула для нахождения спектра модели АР лежит в основе параметрического спектрального оценивания.
Для ее вывода
будем рассматривать процесс АР как
реакцию формирующего фильтра
,
на вход которого подаются некоррелированные
отсчеты
.
Можно показать,
что
-преобразование
передаточной функции АР фильтра имеет
вид
,
(11)
где
,
.
(12)
-преобразования
СПМ выходного и входного процессов
связаны соотношением
.
(13)
Чтобы найти
СПМ выходного АР процесса необходимо
в (13) сделать замену
и положить, что для белого шума
– постоянная величина.
Тогда из (13) следует выражение для параметрической оценки СПМ
.
(14)
Выражение (14) широко используется в параметрическом методе спектрального оценивания.
В качестве параметров, полностью характеризующих спектральную оценку случайного процесса, выступают коэффициенты АР и порядок модели.
Параметрическое спектральное оценивание обладает рядом преимуществ по сравнению с традиционными методами спектрального оценивания. К ним относятся: более высокое спектральное разрешение при использовании коротких выборок, отсутствие боковых лепестков.
С помощью модели АР можно получать спектральные оценки случайных процессов со сложной формой СПМ.
Для этого может быть придется использовать модели АР большого порядка. На основе модели АР легко синтезируются оптимальные фильтры подавления, согласованные не только по частоте и полосе спектра, но и по форме спектра случайного процесса.
Достоинством формулы (14) является возможность анализировать СПМ в аналитическом виде, что невозможно сделать при использовании традиционных методов спектрального оценивания на основе преобразования Фурье.
Например, можно найти формулы для определения частоты максимумов и минимумов СПМ.
Чтобы определить
положение максимума или минимума АР
оценки СПМ, нужно взять производную от
(14) по
и приравнять ее к нулю. Корни полученного
уравнения определяют положение
экстремумов функции СПМ.
При
,
можно показать, что
,
(15)
где
– частота на которой находится максимум
СПМ.
3. Характеристическое уравнение модели авторегрессии
Модель АР, описываемая уравнением (1), может быть представлена в операторной форме
,
(16)
где оператор
АР
имеет вид
.
(17)
Действие оператора сдвига z на текущий отсчет описывается следующим образом
.
(18)
Из условия устойчивости формирующего АР фильтра с рациональной передаточной функцией (11), следует условие стационарности АР процесса. Для проверки стационарности случайного АР процесса используется характеристическое уравнение
.
(19)
Если корни характеристического уравнения (19) лежат внутри единичного круга на комплексной плоскости, то процесс АР удовлетворяет условию стационарности и его корреляционная функция стационарна. Характеристическое уравнение (19) можно представить также в виде
.
(20)
Тогда условие
стационарности заключается в том, что
корни характеристического
уравнения (20)
должны лежать вне единичного круга на
комплексной плоскости.
Используя (19) или (20) оператор АР (17) можно представить в виде
.
(21)
Из (21) следует, что уравнение АР (1) можно записать следующим образом
.
(22)
Сравнивая
(1) и (22) найдем связь между коэффициентами
АР и корнями
характеристического уравнения (20).
Приведем
соответствующие формулы для
:
,
(23a)
;
,
(23б)
;
;
,
(23в)
;
;
;
,
(23г)
где первый индекс в квадратных скобках указывает на соответствующий порядок модели.
Полученные формулы оказываются весьма полезными для определения коэффициентов АР по заданным характеристикам случайного процесса.
Отметим, что корни характеристического уравнения полностью описывают модель АР.
Свойства модели зависят параметров, через которые они выражаются. Если корень действительный, то его можно представить в виде экспоненциальной функции
,
(24а)
где
>
>–
коэффициент демпфирования равный
,
а
-ширина
полосы
-го
пика СПМ.
Тогда действительные корни характеристического уравнения принимают вид
.
(24б)
Комплексные корни характеристического уравнения описываются выражениями
,
,
(25)
где
– собственная частота модели АР с
поправкой на демпфирование, соответствующая
-тому
пику СПМ.
4. Генерация коррелированного случайного процесса
В задачах статистического моделирования часто возникает необходимость генерации случайного процесса с заданной корреляционной функцией или с заданной формой и характеристиками СПМ. Для этих целей эффективно использовать генератор процесса АР, показанный на рис. 2.
Генерация случайного процесса осуществляется методом порождающего случайного процесса.
Порождающий процесс в виде белого шума, обычно с гауссовой функцией распределения, пропускается через формирующий фильтр, параметры которого определяются соответствующей моделью АР.
Рисунок 2. Генератор процесса АР
Для генерации процесса нужно выбрать необходимое количество пиков СПМ. Тогда порядок модели АР равен удвоенному числу пиков. Так, для СПМ с одним пиком на ненулевой частоте, порядок модели равен 2. Для СПМ с двумя пиками порядок модели равен 4.
Затем выбирают частоту пика и его ширину полосы. Вычисленные значения корней характеристического уравнения по формулам (24), используются для нахождения коэффициентов АР.
Для этого корни подставляются в соответствующие выражения (23). Генерация процесса осуществляется с помощью рекуррентного выражения (1) с использованием порождающего белого шума a[t].
Функция распределения a[t] может быть любой, но, как правило, используют нормальное распределение с нулевым математическим ожиданием и единичной дисперсией. Белый шум с нормальным распределением получают из белого шума с равномерным распределением.