Изобарно-изотермический потенциал
9. Определить
изменение изобарно-изотермического
потенциала реакции N>2(г)>
+ 2Н>2>О>(ж)>
= NH>4>NO>2
(ж)> и дать
заключение о направлении ее протекания
при стандартных условиях, если
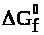для Н>2>О>(ж)>
равна – 237,4
кДж/моль, а для NH>4>NO>2(ж)>
равна – 115,8
кДж/моль.
Решение.
Изобарно-изотермический потенциал реакции рассчитывается так же, как и тепловой эффект реакции – по стандартным теплотам образования веществ:
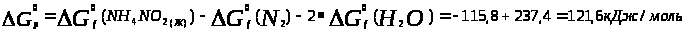
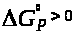Следовательно,
реакция может идти в обратном направлении.
17. При температуре 298 К реакция заканчивается через 2,5 ч. Рассчитать, при какой температуре она закончится через 20 мин., если температурный коэффициент реакции равен 3.
Решение.
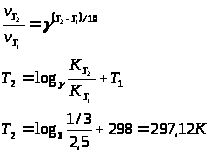
Ответ: 297 К.
25. Уравнение изотермы химической реакции Вант-Гоффа.
В соответствии с законом действующих масс для произвольной реакции
а A + b B = c C + d D
уравнение скорости прямой реакции можно записать:
,
а для скорости обратной
реакции:
.
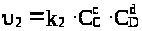По мере протекания реакции слева направо концентрации веществ А и В будут уменьшаться и скорость прямой реакции будет падать. С другой стороны, по мере накопления продуктов реакции C и D скорость реакции справа налево будет расти. Наступает момент, когда скорости υ> 1> и υ> 2> становятся одинаковыми, концентрации всех веществ остаются неизменными, следовательно,
,
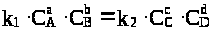Откуда K>c>
= k>1>
/ k>2>
=
.
Постоянная величина К>с>, равная отношению констант скоростей прямой и обратной реакций, количественно описывает состояние равновесия через равновесные концентрации исходных веществ и продуктов их взаимодействия (в степени их стехиометрических коэффициентов) и называется константой равновесия. Константа равновесия является постоянной только для данной температуры, т.е.
К>с> = f (Т). Константу равновесия химической реакции принято выражать отношением, в числителе которого стоит произведение равновесных молярных концентраций продуктов реакции, а в знаменателе – произведение концентраций исходных веществ.
Если компоненты реакции представляют собой смесь идеальных газов, то константа равновесия (К>р>) выражается через парциальные давления компонентов:
K>p>
=
.
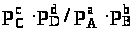Для перехода от К>р> к К>с> воспользуемся уравнением состояния P · V = n·R·T. Поскольку
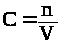, то P
= C·R·T.
Тогда
.
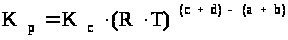Из уравнения следует, что К>р> = К>с> при условии, если реакция идет без изменения числа моль в газовой фазе, т.е. когда (с + d) = (a + b).
Если реакция (1.33) протекает самопроизвольно при постоянных Р и Т или V и Т, то значения G и F этой реакции можно получить из уравнений:
,
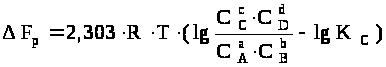где С> А>, С> В>, С> С>, С> >>D> – неравновесные концентрации исходных веществ и продуктов реакции.
,
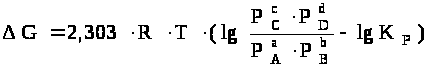где Р> А>, Р> В>, Р> С>, Р> >>D> – парциальные давления исходных веществ и продуктов реакции.
Два последних уравнения называются уравнениями изотермы химической реакции Вант-Гоффа. Это соотношение позволяет рассчитать значения G и F реакции, определить ее направление при различных концентрациях исходных веществ.
Необходимо отметить, что как для газовых систем, так и для растворов, при участии в реакции твердых тел (т.е. для гетерогенных систем) концентрация твердой фазы не входит в выражение для константы равновесия, поскольку эта концентрация практически постоянна. Так, для реакции
2 СО >(г)> = СО >2 (г) > + С >(т) >
константа равновесия записывается в виде
.
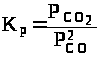Зависимость константы равновесия от температуры (для температуры Т>2> относительно температуры Т>1>) выражается следующим уравнением Вант-Гоффа:
,
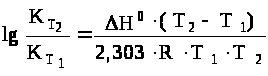где Н0 – тепловой эффект реакции.
Для эндотермической реакции (реакция идет с поглощением тепла) константа равновесия увеличивается с повышением температуры, система как бы сопротивляется нагреванию.
33. Эбулиоскопическая константа воды равна 0,512. Рассчитать, при какой температуре кипит 5 %-ный раствор сахарозы в воде.
Решение.
Повышение температуры кипения раствора
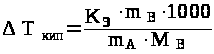
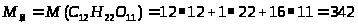г/моль
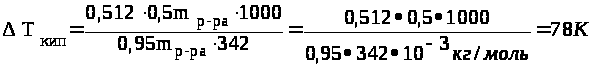
Температура кипения Т = Т>о> +Т>кип>=373 К+78К=451К
59. Свойства дисперсных систем и растворов ВМС, их сходство и отличие. Пояснить, какими путями можно перейти от истинного раствора ВМС к дисперсной системе.
Основными отличительными особенностями дисперсных систем являются:
а) способность к рассеиванию ими света;
б) медленная диффузия частиц дисперсной фазы в дисперсионной среде;
в) способность к диализу;
г) агрегативная неустойчивость дисперсной фазы, которая определяется выделением частиц из дисперсионной среды при добавлении к системе электролитов или под влиянием других внешних воздействий.
Понятие агрегатного состояния не применимо к ВМС, применяется понятие фазового (в структурном смысле) состояния. По сути, понятие фазового состояния характеризует порядок взаимного расположения молекул: ВМС могут находиться в кристаллическом, аморфном и, чрезвычайно редко, в газообразном фазовом состояниях, причем наиболее типичным является аморфное состояние. Последнее дополнительно подразделяется на стеклообразное, высокоэластическое и вязкотекучее. Переход из одного состояния в другое всегда протекает не резко, а в некотором интервале температур.
При помещении ВМС в растворитель происходит поглощение растворителя и соответствующее увеличение объема и массы полимера, идет процесс набухания.
Если каким-либо способом воспрепятствовать увеличению объема ВМС при его набухании, то со стороны ВМС может проявляться чрезвычайно высокое давление набухания, достигающее нескольких атмосфер (пример – дробление скал древесными клиньями, заливаемыми водой).
Процесс набухания высокомолекулярного вещества связан с взаимодействием макромолекул с молекулами растворителя, и степень набухания ВМС зависит как от природы ВМС, так и от природы растворителя. Набухание полярного ВМС протекает только в полярном растворителе, а неполярного – только в неполярном (полезно вспомнить эмпирическое правило: подобное растворяется в подобном).
Добавление к истинному раствору ВМС электролитов уменьшает сольватирующую способность растворителя – в итоге система может быть нарушена, т.е. может произойти выделение высокомолекулярного вещества из раствора, и полимер как бы отделится от растворителя (появляются волокна, хлопья, творожистые осадки). Этот процесс называется высаливанием.
Механизм высаливания состоит в том, что сольватирующие ВМС молекулы растворителя начинают взаимодействовать с электролитом, сольватная оболочка около макромолекулы разрушается, происходит десольватация макромолекулы и, как следствие, резко снижается растворимость ВМС, т.е. происходит его высаливание. Способность ВМС высаливаться из растворителя резко возрастает с увеличением молярной массы полимера. На этом основано фракционирование полидисперсного ВМС по молярной массе (используется, в частности, для разделения смеси белков различной молярной массы).
Процесс высаливания может приводить к появлению в системе другой жидкой студнеобразной фазы в виде мельчайших капель, концентрация ВМС в которых выше, чем в исходном растворе.
Растворам ВМС свойственно осмотическое давление, которое, однако, значительно выше, чем рассчитываемое по уравнению Вант-Гоффа Это связано с тем, что роль кинетического элемента могут играть в одной макромолекуле сразу несколько ее сегментов. Поэтому значение осмотического давления будет повышаться с увеличением гибкости макромолекулы. На использовании этого явления разработан метод определения молярных масс высокополимеров в разбавленных растворах путем измерения в растворе осмотического давления.
Макромолекулы ВМС обладают диффузионной способностью, близкой к диффузии компонентов в дисперсных системах.
Многие ВМС содержат ионогенные (т.е. способные образовывать ионы) группы, поэтому представляют собой полиэлектролиты (полимерные электролиты), склонные к ионизации в растворе. Так, растворимый крахмал содержит в макромолекуле кислотные – СООН-группы, а агар-агар –SО>3>Н-группы, которые в растворе могут диссоциировать с отщеплением иона водорода. Некоторые ВМС имеют в своем составе основные –NН>2> или (при присоединении молекулы воды) –NН>3>ОН-группы. Таким образом, длинная молекула высокомолекулярного электролита, продиссоциировавшая в воде, представляет собой один полиион с жестко закрепленными фиксированными –СОО ¯, –NН>3>+– или другими ионами, а около этой полимерной цепочки располагаются подвижные противоионы, заряды которых эквивалентны заряду полииона. Обычно на одно элементарное звено макромолекулы ионогенного полимера приходится одна ионогенная группа. Две ионогенные группы (–СООН и –NН>3>ОН) в своем составе имеют белки, причем в большинстве белков соотношение этих групп неодинаково. Так, в растворах глиадина пшеницы, протамина и других превалируют основные группы, а в таких белках, как казеин, коллаген, альбумин и других преобладают ионогенные группы кислотной природы. Молекулу белка можно схематично изобразить:
НОН>3>N – R – СООН,
где R – длинная углеводородная цепочка, содержащая также группы – СОNН–.
Ионогенные группы кислотной и основной природы могут располагаться не только по краям, но и внутри молекулы белка. Полипептидная цепь белков состоит из многих десятков и даже сотен аминокислот в различных сочетаниях, что обусловливает многообразие белков. Амино- и карбоксильные группы полипептидных цепей могут взаимодействовать между собой, образуя водородные связи. Эти связи образуются как между отдельными молекулами, так и внутри одной молекулы, а также и с молекулами растворителя. Глобулярные белки (макромолекулы шаровидной или эллипсоидной формы) – это альбумин, глобулины яичного белка, молока, сыворотки крови, пепсин желудочного сока. Молекулы коллагена и желатина (составная часть тканей кожи и сухожилий) имеют форму тонких вытянутых нитей.
В зависимости от рН раствора кислотная и основная группы проявляют различную склонность к диссоциации. В кислых растворах больше диссоциирована основная группа, в щелочной среде – кислотная. Когда в молекуле белка диссоциированы в основном кислотные группы, макромолекула имеет отрицательный заряд и в постоянном электрическом поле при электрофорезе будет передвигаться в сторону анода. Диссоциация основных и кислотных групп происходит в одинаковой степени в белке только при определенном значении рН раствора, это значение рН (обычно ниже 7) называется изоэлектрической точкой (ИЭТ). Такое изоэлектрическое состояние белка с ионизированными ионогенными группами можно изобразить следующим образом:
ОН + Н>3>N – R – СОО + Н.
Разделение белков по фракциям методом высаливания проводят обычно вблизи изоэлектрической точки, т.е. при определенных значениях рН в растворе. По достижении изоэлектрической точки, когда кулоновское взаимодействие групп разного заряда происходит уже по всей длине цепи, молекула белка сворачивается в клубок.
Денатурация – необратимая коагуляция белка, вызываемая, например, его нагреванием, добавлением спирта, действием световой энергии и др. Этот вид коагуляции характерен (из лиофильных коллоидов) только для белковых веществ. Так, необратимое изменение свойств яичного белка при его термической обработке (достаточно 60 – 65 оС) происходит только в присутствии воды, тогда как сухой яичный белок не денатурируется при температуре 100 оС и даже выше.
Процесс термической денатурации белка, который характерен для белков глобулярного типа, обусловлен разрывом слабых водородных связей внутри глобулы и последующим распрямлением и вытягиванием макромолекулы. При этом вследствие изменения структуры белка изменяются и его свойства, в частности повышается вязкость раствора и понижается растворимость полимера.
Несмотря на схожесть процессов денатурации и высаливания белков, у них имеется и важное отличие: денатурация необратима, а высаливание обратимо.
Свойства дисперсных систем и ВМС имеют сходства и отличия.
Сходства: как и дисперсные системы, ВМС присущи явления осмоса, диффузии и коагуляции (обратимой и необратимой).
Различия: явления высаливания и денатурации присущи только ВМС.
Процессом образования дисперсных систем из ВМС можно считать процесс высаливания.
67. Определить частичную концентрацию гидрозоля Al>2>O>3>, если его массовая концентрация 0,3 г/л, коэффициент диффузии сферических частиц золя 2·10-6 м2/сут., плотность гидрозоля 4 г/см3, вязкость дисперсионной среды 10-3 н·с/м2 и температура 293 К.
Из уравнения Эйнштейна
радиус частицы:
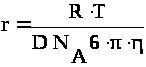
где N>А> – число Авогадро, 6 10 23 молекул/моль;
– вязкость дисперсионной среды, Н с/м2(Па с);
r – радиус частицы, м;
R – универсальная газовая постоянная, 8,314 Дж/моль · К;
T – абсолютная температура, К;
число 3,14.
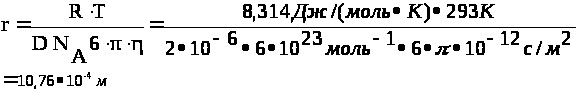
Находим массу частицы:
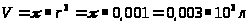
Находим концентрацию частицы:
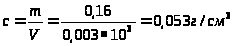
Ответ: 0,053 г/см3
75. Адсорбция на поверхности раздела Ж/Г. Адсорбционное уравнение Гиббса, его анализ и область использования. Адсорбция – процесс самопроизвольного поглощения вещества (адсорбтива) поверхностью адсорбента. Уравнение Гиббса устанавливает взаимосвязь величины адсорбции (Г,кмоль/кг или кмоль/м2) с изменением поверхностного натяжения (Дж/м2 от концентрации раствора (С, кмоль/л).
,
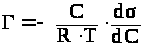где С – концентрация раствора, кмоль/л;
R – универсальная газовая постоянная;
T – температура;
d/dС – производная, являющаяся мерой поверхностной активности; может быть определена графически по зависимости поверхностного натяжения от концентрации (при 0).
Адсорбция на жидкой поверхности может приводить как к уменьшению поверхностного натяжения (например, при адсорбции малорастворимых, дифильных поверхностно-активных веществ), так и к его увеличению (в частности, при адсорбции поверхностно-инактивных веществ, т. е. хорошо растворимых в воде неорганических электролитов) или не изменять его (растворы сахаров в воде). В последнем случае вещество распределяется равномерно между поверхностным слоем и объемом раствора.
83. Написать формулы мицелл: Al(OH)>3>, стабилизированной AlCl>3>; SiO>2>, стабилизированной H>2>SiO>3>. Для какой из указанных мицелл лучшим коагулятором является FeCl>3>, Na>2>SO>4>?
[m
(SiO>2>)
n Si4+
(n -x)
2-]х+
x
–
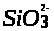[m (AlCl>3>) n Cl– · (n -x) Al3+]х– x Al3+) Лучшим коагулятором будет FeCl>3>.
94. Защита коллоидных частиц с использованием ВМС. Механизм защитного действия. Белки, углеводы, пектины как коллоидная защита.
Коллоидная защита – стабилизация дисперсной системы путем образования адсорбционной защитной оболочки вокруг частиц дисперсной фазы. Белки, пектины и углеводы выступают как стабилизаторы дисперсных систем, предохраняющих системы от дальнейшей коагуляции или седиментации.
103. Студни как эластичные гели. Механизм их образования и факторы, определяющие скорость студнеобразования. Процессы студнеобразования в пищевой технологии.
Студни – это ограниченно набухшие полимеры, их можно рассматривать как частную форму эластичных гелей. Студни – гомогенные системы, они нетиксотропны. Жидкость, заполняющая сетку студня, называется интермицеллярной жидкостью.
Растворы ВМС в некоторых условиях (изменение температуры, концентрирование раствора или при добавлении небольшого количества электролита) могут самопроизвольно терять свою текучесть и переходить в студни, т.е. в систему с некоторыми свойствами твердого тела. Причина такого перехода – возникновение связей между макромолекулами ВМС за счет целого спектра молекулярных контактов. Структура студней образована за счет дисперсионных сил и водородных связей, также в ее создании принимают участие и обычные химические связи. Первоначально в растворе образуются кратковременные ассоциаты из макромолекул как за счет взаимодействия гидрофильных участков макромолекул, так и за счет молекулярных контактов между гидрофобными частями разных молекул. Когда время существования ассоциатов становится весьма продолжительным, то система с созданной пространственной сеткой начинает проявлять свойства твердой фазы.
Студни образуются также в результате ограниченного набухания или вследствие охлаждения раствора ВМС. При нагревании каркас студня разрушается и система снова разжижается. Этот же эффект достигается и путем механического воздействия на систему – перемешиванием или встряхиванием.
Если в студень, содержащий в свободной воде низкомолекулярное вещество, диффундирует другое, способное образовывать с первым нерастворимое соединение, то реакция осаждения идет только в определенных зонах структуры студня. В результате в студне наблюдаются слои или кольца, образованные этим осадком.
Электропроводность студней близка к электропроводности растворов, из которых эти студни были получены, то есть трехмерная сетка, образующаяся в студне, не мешает движению сравнительно маленьких ионов через его раствор.
Старение студней, как и гелей, проявляется в виде явления, которое носит название синерезис. Явление синерезиса характерно как для студней, так и для эластичных гелей (например, отделение сыворотки при свертывании молока, «слеза» в сыре и др.).
Синерезис – это самопроизвольное выделение жидкости из геля, т.е. это явление, обратное набуханию. Многие гели, особенно тиксотропные, с низким содержанием дисперсной фазы со временем сжимаются и выделяют часть интермицеллярной жидкости. В результате процесса синерезиса, являющегося отображением непрочного состояния жидкости в гелях, образуются 2 фазы – жидкая (раствор ВМС в растворителе) и студнеобразная (раствор растворителя в ВМС). Например, жидкость, выделяющаяся после образования простокваши, является слабоконцентрированным золем.
В процессе синерезиса происходит сближение частиц, сжатие каркаса геля и выдавливание из него в первую очередь свободной воды. Явлению синерезиса благоприятствуют все факторы, которые способствуют коагуляции. Это, в частности, повышение числа частиц в растворе, добавление к нему спирта, повышение температуры и др.
ЛИТЕРАТУРА
Ахметов Б. В. Задачи и упражнения по физической и коллоидной химии. – Л.: Химия, 1989.
Гамеева О. С. Физическая и коллоидная химия. – М.: Высшая школа, 1983.
Евстратова К. И., Купина Н. А., Малахова Е. М. Физическая и коллоидная химия. – М.: Высшая школа, 1990.
Зимон А. Д., Лещенко Н. Ф. Коллоидная химия. – М.: Химия, 2001.
Зимон А. Д., Лещенко Н. Ф. Физическая химия. – М.: Химия, 2000.
Киселев Е. В. Сборник примеров и задач по физической химии. – М.: Высшая школа, 1983.
Кнорре Д. Г. Физическая химия. – М.: Высшая школа, 1990.
Стромберг А. Г. Физическая химия. – М.: Высшая школа, 2001.
Степин Б. Д. Международные системы единиц физических величин в химии. – М.: Высшая школа, 1990.
Фридрихсберг Д. А. Курс коллоидной химии. – Л.: Химия, 1995.
Хмельницкий Р. А. Физическая и коллоидная химиия. – М.: Высшая школа, 1988.