Измерение набухания слабосшитых гидрогелей
ИЗМЕРЕНИЕ НАБУХАНИЯ СЛАБОСШИТЫХ ГИДРОГЕЛЕЙ
Новое поколение влагопоглощающих полимеров — сильнонабухающие полимерные гидрогели (СПГ) представляют собой, как правило, полиэлектролитные сетки с низкой плотностью узлов сшивания. Большой интерес, проявляемый в последнее время к такого рода полимерам, обусловлен, с одной стороны, значительным прогрессом в теории заряженных сеток, с другой - рядом важных практических аспектов, среди которых агромелиорация засушливых почв, новые технологии растениеводства, влагопоглощающие материалы и изделия санитарного назначения, некоторые биомедицинские применения.
Усовершенствование способов синтеза и регулирования структуры СПГ, их подбор для решения той или иной практической задачи в значительной степени определяются возможностью количественной оценки набухания гидрогелей в широком интервале внешних условий, поскольку именно набухание является наиболее важной характеристикой СПГ и прямо связано с их структурой. Измерение степени набухания w в интервале 103—104 мл/г является, однако, экспериментальной проблемой. Традиционные подходы в строгом смысле здесь абсолютно неприменимы, и единственный из разработанных способов — измерение размеров объектов правильной геометрической формы (сферы, цилиндра, шайбы) более или менее приемлем в этом масштабе степеней набухания [1, 2], но и он наталкивается на трудности, обусловленные необходимостью визуализации границы образца.
Развитие теоретических и прикладных исследований в области СПГ требует, таким образом, модификации и усовершенствования соответствующих измерительных процедур. В настоящей работе рассмотрены новые экспериментальные методы, разработанные специально для характеристики СПГ, а также результаты их апробации на типичных объектах.
Свободное набухание. Набухание гидрогеля при отсутствии каких-либо воздействующих на образец нагрузок называют свободным. В случае СПГ оно реализуется при набухании в избытке жидкости, поскольку различия в плотности набухшего образца и окружающего раствора в этом случае пренебрежимо малы (~2-10~4 г/мл при набухании 1 л/г).
При разработке методики измерений свободного набухания было необходимо прежде всего исключить операции переноса образца, обладающего крайне низкой механической прочностью, из жидкости и обратно для измерений его объема или массы. Обычно эти операции сопряжены с потерей части образца. Необходимым требованием было также максимальное снижение размера исходного образца СПГ, что позволило бы сократить время достижения равновесного набухания, в большинстве случаев весьма продолжительное.
Этим и ряду других методологических требований удовлетворяет установка для измерений набухания, схематически представленная на рис. 1. Образец геля 1 в виде нескольких крупинок помещают на сетку 2. В калиброванный цилиндр 3 при крайнем верхнем положении поршня 4 наливают определенное количество (~8 мл) воды или раствора, в которых необходимо измерить набухание, причем исследуемый образец оказывается полностью погруженным в жидкость. Каждые 20 мин блок автоматики 5 включает двигатель 6, опускающий поршень до тех пор, пока уровень жидкости не пересечет луч оптической пары 7. Соединенное с поршнем перо самописца 8 регистрирует в этот момент объем жидкости, поглощенной образцом. Поршень автоматически возвращается затем в исходное верхнее положение, причем весь цикл его движения занимает около 3 мин. Совокупность точек образует на ленте самописца кинетическую кривую набухания 9, содержащую информацию о величине равновесной степени набухания и о темпе ее достижения, т. е. характерном времени набухания. Типичные кинетические кривые, полученные этим методом, опубликованы ранее [3].
Принципиальные погрешности метода на величине степени набухания определяются прежде всего удержанием некоторого количества жидкости за счет капиллярных сил на сетке и в контактах между частицами образца, а также потерями жидкости на испарение и истечение через поршень. Специальными опытами показано, что суммарная погрешность за счет всех указанных факторов составляет ~0,1 мл, т. е. не более 3% при работе в основной части шкалы самописца. Общая погрешность метода с учетом взятия навески <5%. Дополнительным указанием на корректность измерений степени набухания является совпадение результатов данного и оптического [3] методов соответственно 1600±120 и 1540±80 мл/г для одного из образцов.
На рис. 2 приведены результаты измерения данным методом степени набухания одного из типичных полиакриламидных гидрогелей. Как видно, зависимость объема поглощенной жидкости от массы образца линейна, что отражает постоянство величины степени набухания, равной в этом случае 1800=30 мл/г. Эти результаты наглядно демонстрируют измерительные возможности установки.
Несомненным удобством данной методики, в которой образец постоянно находится на сетке и не перемещается при измерениях, является возможность наблюдать и количественно регистрировать изменение набухания СПГ при любой вариации внешней среды. Рисунок 3 показывает в качестве примера диаграмму опыта по измерению набухания СПГ в ходе ступенчатого разбавления раствора NaCl, первоначальная концентрация которого составляла 3 моль/л. Эксперимент демонстрирует характерное для полиэлектролитных гидрогелей ионное подавление, обусловленное эффектом Доннана и детально описанное в литературе [3—5]. Аналогичным образцом в рамках данного метода может быть исследован коллапс СПГ под действием многовалентных ионов, добавок растворителей и т. п.
Анализ кинетических кривых набухания [3] показывает, что при прочих равных условиях характерное время набухания т зависит от размера частиц образца. В частности, при свободном набухании в воде для образцов с равновесной степенью набухания 1 л/г и исходным радиусом частиц от 0,25 до 0,5 мм величины т составляют от 11 до 42 мии. Отсюда возникает требование снижения размера образца и оптимальным оказываются частицы радиусом ~0,5 мм, что обеспечивает измерение равновесного набухания за период ~5т, т. е. за 200 мин.
Опыт работы с лабораторной установкой, основанной на описанных принципах, показал, что в сравнении с традиционными методами взвешивания образцов или измерения их объема с предварительным отделением свободной жидкости она значительно повышает надежность и производительность эксперимента. Обладая большой вариабельностью в исследовательских задачах, предлагаемый метод весьма удобен для экспрессного тестирования и сопоставления СПГ, различающихся природой или способом получения, а также для корректной оценки результатов синтеза, в сочетании с теоретическими соотношениями для набухания полиэлектролитных гелей [3, 6] полученные экспериментальные данные могут быть надежным источником сведений о структуре сетки в СПГ.
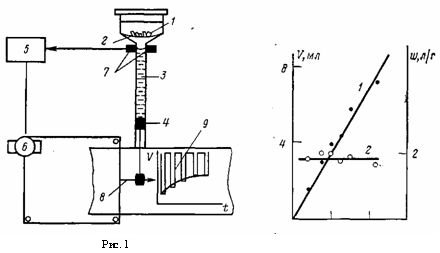
Рис. 1. Прибор для автоматической регистрации набухания гидрогелей. Зависимость объема V жидкости (10~4 н. раствор NaCI), поглощенном при набухании (1) и степени набухания w (2) от массы образца Л
Давление набухания. Давление набухания я является важным источником информации о структуре сетчатых полимеров, в том числе гидрогелей (7, 8]. Интерпретация функции я (if) для нейтральных сеток позволяет независимо оценивать, например, параметр взаимодействия % и плотность узлов сетки п>с>.
Для прямого измерения давления набухания обычно применяют устройства, в которых сшитый полимер, например каучук [9], набухает в цилиндрическом сосуде с поршнем, контактируя с растворителем через пористую перегородку. Конкретная конструкция прибора определяется интервалом давлений и свойствами, точнее, упругостью набухшего образца. В случае полимеров с высокой плотностью сшивания применение этой методики не вызывает особых затруднений [7, 9].
Тот же экспериментальный подход в приложении к СПГ наталкивается на ряд проблем, среди которых измерение малых давлений и низкие модули упругости образца создают наиболее серьезные осложнения. Здесь явно требуется компромисс между необходимостью снижения трения в поршне, с одной стороны, и сохранением герметичности системы по отношению к весьма «мягким» частицам геля - с другой.
Для измерений давления набухания СПГ предложен [3] несколько модифицированный прибор, работающий по тому же принципу. Первоначально измерения на этом приборе проводили, задавая с помощью системы противовесов определенное давление поршня на гель и регистрируя динамику приближения объема образца к равновесному. В этом варианте метода на конечной стадии, т. е. вблизи равновесия возникали погрешности, обусловленные трением поршня, которые лишь частично удавалось устранять подключением системы к малоамплитудному вибртору и улучшением механической обработки поверхностей поршня и цилиндра.
В усовершенствованном варианте того же метода наблюдали за изменением давления в ходе приближения к равновесию при заданном объеме геля. При этом величину давления в выбранный момент времени определяли из зависимости скорости перемещения поршня от малых положительных и отрицательных вариаций нагрузки (рис. 4, а), а именно из точки пересечения прямой с осью абсцисс. Неопределенность, связанная с наличием трения покоя, в этом масштабе не проявляется, но из рис. 4, б, где показана та же зависимость, полученная в отсутствие геля, видно, что эта погрешность может быть сведена к 20-40 Па (2-4 мм Н>2>О).
Измеряемое таким образом давление возрастает во времени, стремясь к равновесному значению π. Зависимость я от объема системы при известном весе исходного образца превращается в кривую я (if), показанную для одного из СПГ на рис. 5. Ее интерпретация, как уже отмечалось, с помощью соответствующих уравнений (например, уравнения Флори - Реннера для неионизованных гелей) может дать параметры внутренней структуры. Сплошная кривая на рис. 5 получена расчетом по уравнениям теории набухания полиэлектролитных гелей [3] при следующих значениях параметров сетки: х=0,48, п>с>=3,610-5 -моль/мл, доля ионных групп β=0,25, их константа диссоциации π> н>=7 10~8 моль/л. Как видно, расчетная кривая хорошо описывает всю совокупность экспериментальных точек.
Если оценивать диапазон работоспособности предлагаемой методики применительно к СПГ, то он определяется в первую очередь невозможностью удержать гель

Рис. 3. Динамика набухания гидрогеля (образец Б) в водном растворе NaCl при ступенчатом изменении концентрации: 3,0 (2); 0,90 (2); 0,27 (3); 0,08 (4); 0,034 (5) и 0,015 н. (в)

Рис. 4. Зависимость скорости перемещения поршня от давления на поршень, а: образец В, w=102 (1), 37 мл/г (2), продолжительность набухания 51 (1) и 7 сут (2). б: 3 — свободное движение поршня, 4 - движение поршня с подключением г; вибратору

Рис. 5. Зависимость давления набухания образца Б в 0,01 н. растворе NaCl от степени набухания в условиях равновесия с очень высоким набуханием или при высоком давлении в замкнутом для него пространстве между поршнем и дном цилиндра.
Проведенные эксперименты показывают, что величины 30 кПа и 600 — 700 мл/г являются предельными для данного варианта. Отметим, что в литературе, где измерениям давления набухания гидрогелей уделено серьезное внимание, данные для гелей с такими показателями отсутствуют. Изучение функции λ в области еще больших значений набухания требует каких-то новых подходов.
Необходимо отметить, что наряду с «диагностической» ценностью зависимости набухания СПГ от давления она имеет самое непосредственное отношение к их практическим использованиям. Например, в случае применения СПГ в качестве почвенного влагоабсорбера или в растениеводческих задачах необходимо, чтобы давление набухания и прямо связанный с ним термодинамический потенциал влаги в СПГ согласовались с аналогичными возможностями почвы и растений [10]. Такой подход позволяет анализировать свойства и поведение СПГ в реальных условиях применения с единых, термодинамических позиций, причем функция λ (w) играет здесь ключевую роль.
Анализ зависимостей я (I) показывает, что время релаксации давления набухания т>я>, как и т возрастает с увеличением размера образца. Типичное для используемой конструкции прибора значение эффективного размера R>e>, который определяется радиусом и толщиной цилиндрического слоя геля, составляет ~1 см, а значение т>я> = 70 ч. т. о. весьма велико, причем возможности его снижения за счет уменьшения массы образца в данном случае ограничены.
Наблюдаемые кинетические характеристики набухания могут быть интерпретированы в рамках имеющихся теоретических подходов. Согласно работе [11], т и равновесный размер образца при свободном набухании Л„ связаны соотношением где D - коэффициент кооперативной диффузии.

Используя тот же подход, можно показать, что для давления набухания справедливо аналогичное уравнение
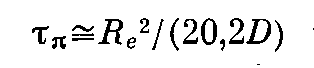
Обработка экспериментальных зависимостей т>я>(Л>е>), согласно уравнению (2), приводит к величине D= (2,4±0,6) -10~7 см2/с, которая близка к опубликованным значениям коэффициентов кооперативной диффузии [11-13]. Напротив, зависимости для того же образца в рамках уравнения (1) дают существенно более высокое значение D= (1,0±0,2) -10-5 см2/с, которое в свою очередь хорошо согласуется с величиной полученной из динамики длины волны рельефа, возникающего на поверхности СПГ в результате потери механической устойчивости при набухании [14].
Отмеченное расхождение в величинах D отчасти может быть связано с тем, что в качестве размера цилиндрических образцов СПГ использовали радиус шара с тем же объемом, хотя вряд ли это может объяснить расхождение на порядки величин. Более существенным может быть то, что имеющиеся теоретические соотношения [11] описывают процесс набухания при малых отклонениях исходного размера частиц от равновесного. В наших же экспериментах они различаются в 2-4 раза, причем в состояниях, далеких от равновесия, гель теряет механическую устойчивость [14, 15], и набухание нельзя свести только к кооперативной диффузии фрагментов сетки в растворителе.
Проведенный беглый анализ динамики набухания СПГ показывает, что для ее более глубокого понимания необходимы дополнительные исследования, поскольку здесь имеются нетривиальные эффекты. В качестве экспериментальной базы этих исследований вполне могут быть использованы развитые в данной работе методы.
В работе использовали СПГ на основе полиакриламида, содержащего небольшое количество (<30 мол.%) звеньев акриловой кислоты, образующих при диссоциации связанные с сеткой заряды, что в значительной мере определяет масштаб набухания. Образцы получали двумя типичными для таких полимеров методами.
Образец А. Трехмерную сополимеризацию смеси акриламида, акриловой кислоты и NN-метилен-бис-акриламида как разветвителя, очищенных как в работе [16], проводили в 10%-ном водном растворе мономеров под действием инициирующей системы, состоящей из персульфата аммония и тетрамотилэтилендиамина (2 : 1 в молях). Содержание разветвителя в сумме мономеров составляло 0,13 мол.%, концентрация инициатора 8,8-10-4 моль/л, температура 45°. Конверсия мономеров по данным спектрофотометрии превышала 99%.
Образец Б. Радиационное сшивание линейного полиакриламида, содержащего 25— 30% тех же ионогенных групп, проводили в 5-10Уо-ных водных растворах под действием Y-лучей 60Со в стандартных установках при дозах до 10 Мрад. Содержание зольфракции в радиационно сшитых образцах, определенное весовым методом, было <10-15%.
Полученный тем или иным методом гидрогель механически измельчали и использовали для измерений непосредственно либо после высушивания на воздухе до постоянного веса.
Все описанные измерения проводили при комнатной температуре.
СПИСОК ЛИТЕРАТУРЫ
Huglin М. В., Zakaria М. В. // J. Appl. Polymer Sci. 1983. V. 28. № 7. P. 2451.
Mateescu M. A., Schell H. D., Dimonie M., Todireanu S., Maior O. // Polymer Bull. 1984. V. 11. № 5. P. 421.
Дубровский С. А., Афанасьева M. В., Рыжкин М. А., Казанский К. С. //Высокомолек. соед. А. 1989. Т. 31. № 2. С. 321.
Ricka J., Tanaka Т. // Macromolecules. 1984. V. 17. № 12. P. 2916.
Marlnsky J. А. // Phys. Chem. 1985. V. 89. № 24. P. 5294.
Flory P. J. Principles of Polymer Chemistry. Ithaca; N. Y., 1953. 672 p.
Hydrogels for Medical and Related Applications/Ed. by Andrade J. D. Washington, 1976. № 31.
Borchard W., Embergen A., Schwarz J. // Angew. Makromolek. Chemic. 1978. B. 66. S. 43.
Сурдутович Л. И., Тагер А. А., Овчинникова Г. П., Хомякова Н. И., Сафонов Я. А.Ц Высокомолек. соед. А. 1972. Т. 14. № 2. С. 324.
Казанский К. С, Ракова Г. В., Ениколопов Н. С, Агафонов О. А., Романов И. А., Усков И. Б. Вестн. с.-х. науки. 1988. № 4(380). С. 125.
Tanaka Т., Fillmore G. // J. Chem. Soc. 1979. V. 70. № 3. P. 1214.
Peters A., Candau S. // Macromolecules. 1986. V. 19. № 7. P. 1952.
Munch J. P., Candau S., Duplessix R., Picot C, Herz J., Benolt H.//L Polymer Sci, Polymer Phys. Ed. 1976. V. 14. № 6. P. 1097.
Дубровский С. A. // Докл. АН СССР. 1988. Т. 303. № 5. С. 1163.
Tanaka Т., Sun S.-T., Hirokawa Y., Katayama F., Kufera J., Hiroce Y., Amija Т.Ц Nature. 1987. V. 325. № 6107. P. 796.
Watkin J. E., Miller R. A. // Anal. Biochem. 1970. V. 34. № 2. P. 424.