Гетерогенный катализ

TYPE=RANDOM FORMAT=ARABIC>13


Гетерогенный катализ.

Гомогенно-каталитизируемое превращение протекает в одной фазе, где смешаны и реагенты, и катализатор, и продукты. В гетерогенно-катализируемом превращении катализа-тор образует отдельную фазу, а химический элементарный акт протекает на её поверхности и пространственно как бы отделён от основной массы и реагентов, и продуктов. Поэтому для кинетического моделирования этого сложного превращения его необходимо представить как результат суперпозиции нескольких элементарных процессов. Это:

- 1) Диффузия реагента из объёма к поверхности катализатора (массоперенос).

- 2) Адсорбция реагента на поверхности катализатора.

- 3) Химическое превращение реагента в продукт на поверхности катализатора.

- 4) Десорбция продукта с поверхности катализатора.

- 5) Диффузия продукта от поверхности катализатора в объём (массоперенос).

Эти элементарные процессы удобно математически вначале смоделировать по отдельности:

Диффузия из объёма к поверхности

(12.1)

; (12.2)

Уравнение массопереноса под влиянием диффузии имеет первый порядок по концентрации. Формально оно не отличается от обычного кинетического уравнения. Диффузия - процесс активационный с относительно небольшой энергией активации - всего около 4-9 кДж/моль.

2) Режим диффузионнный и режим кинетический.

В стационарном режиме скорость химического превращения на поверхности равна скорости диффузии вещества из объёма к поверхности:

; (12.3)

Отсюда появляется две возможности -два возможных режима процесса:

(12.4)

3)Адсорбция на поверхности. Уравнение Лангмюра для одного адсорбата.

; ; ; (12.5)

Кривая Лангмюра в области начала кривой адсорбции может быть заменено более простым уравнением Бедекера-Фрейндлиха:

Рис.24. Кривая адсорбции.

3.1) Адсорбция на поверхности.

Уравнение Лангмюра для нескольких адсорбатов.

В таком случае

(12.6) ® ( масса/площадь)

0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010022000000000001000000180300000000000018030000010000006c0000000000000000000000350000006f00000000000000000000005c1400001612000020454d4600000100180300001200000002000000000000000000000000000000c0120000131a0000cb0000001b010000000000000000000000000000f818030078510400160000000c000000180000000a0000001000000000000000000000000900000010000000cf04000046040000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000a4ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100dc5f11001000000040631100c060110052516032406311003860110010000000a8611100246311002451603240631100386011002000000049642f31386011004063110020000000ffffffffbc53e600d0642f31ffffffffffff0180ffff01800fff0180ffffffff0000000000080000000800001cbb120001000000000000005802000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c00690062007200000000000000000000611100dee32e31e88d0832606411006c6011009c3827310800000001000000a8601100a8601100e878253108000000d0601100bc53e6006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c0000000000000254000000540000000000000000000000350000006f0000000100000055558740a0ab87400000000057000000010000004c000000040000000000000000000000cf04000046040000500000002000d5003600000046000000280000001c0000004744494302000000ffffffffffffffffcf04000047040000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02b100c700040000002e0118001c000000fb020300010000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0e0000000100040000000000c700b10020df0900040000002d010000040000002d010000030000000000

Это уравнение полезно для формально-кинетического описания гетерогенно-каталитических реакций

3.2) Активированная адсорбция.

Изобара Тэйлора. Хемосорбция.

Пример высокой энергии активации при адсорбции и её причины. Е*=40-80 кДж/моль. Кривая хемосорбции отражает смешанный механизм поглощения вещества поверхностью и не имеет точного количественного описания.



Рис.26. Изобара

хемосорбции.

4) Поверхностный гетерогенно-каталитический процесс (общие сведения).

. (12.7)

(12.8)

(12.9)

4.1) Поверхностный гетерогенно-каталитический процесс (частная модель).

(Механизм Лангмюра-Хиншельвуда для гетерогенно-каталитической реакции)

Для гетерогенно-каталитической реакции формулы 12.9 означают:

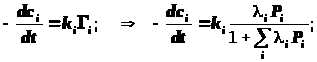(12.10)

4.2.1) Рассмотрим частные случаи. Для определённости выделим пару реагент-продукт:

, где . (12.11)

Основные случаи следующие:

1) Продукт M адсорбируется слабее реагента A:

а) Наблюдаем:1-й порядок по реагенту A

б) Наблюдаем: 0-й порядок по реагенту A

2) Реагент A адсорбируется слабее продукта, а продукт M адсорбируется очень сильно: Продукт M тормозит реакцию.

4.3) Приведём несколько различных вариантов протекания гетерогенного катализа в реакциях разложения соединений на металлических катализаторах. (см. А.В. Раковский, Курс физической химии, стр.510-511):

4.3.1. Слабая адсорбция. Молекулы покрывают лишь малую часть катализатора:

Так протекает разложение Порядок первый.

4.3.2. Средняя адсорбция реагирующего газа: Разложение . Порядок дробный - согласуется с уравнением адсорбции Бедекера- Фрейндлиха.

4.3.3. Реагирующее вещество адсорбируется слабо, а продукт со средней силой:

4.3.4. Реагирующий газ адсорбируется слабо, продукт сильно:

на Pt :

4.3.5. Реагирующий газ адсорбируется сильно:

на W: нулевой порядок по аммиаку.

Рассмотрим классический пример – газофазную реакцию: H>2>+1/2O> 2>= H>2>O

Истинный механизм этой реакции состоит из многих стадий (до 30). Существуют различные подходы к его описанию. Выделим лишь некоторые наиболее характерные стадии, и введём очень упрощённую модельную схему, пригодную для классификации основных элементарных превращений, и с их помощью выделим главные особенности и выявим возможные режимы протекания всего процесса. Они возникают из-за конкуренции стадий разветвления и обрыва. Приводимый ниже механизм реализуется при невысоких давлениях (несколько десятков тор) (см. М.Н. Варгафтик, «Химическая кинетика» кафедральное пособие МИТХТ под ред. акад. Я.К. Сыркина, 1970, стр. 89, а также учебник «Физическая химия» под ред. К.С. Краснова, стр. 608). Основные стадии представим в нижеследующей таблице.

Упрощённый механизм разветвлённой цепной реакции

H>2>+O>2>= H>2>O

Баланс активных центров

на отдельных стадиях

Скорости элементарных стадий

№

Элементарные реакции

Исх.

Кон.

Скорость

Природа стадии

1

H>2>

+ O>2 >

2 HO·

· ·

r>1>=k>1>[H>2>][O>2>]

Зарождение

2

HO·

+ H> 2 >

H>2>O

+ H·

·

·

r>2>=k>2>[H> 2>][HO·]

Продолжение

3

H·

+ O> 2 >

HO·

+ O··

· ·

· ( · ·)

r>3>=k>3>[O>2>][H·]

Разветвление

4

O··

+ H>2 >> >

HO·

+ H·

( · ·)

· ·

r>4>=k>4>[H>2>][O··]

5

H·

+ O>2 >+ M 

HO>2 >·

+ M

·

(·)

r>5>=k>5>[M][O>2>][H·]

квадрат.

Обрыв

6

H·

+ M> >

1/2 H>2>

+ M

·

r>6>=k>6>[M][H·]

линейн.

Стадия 4 считается разветвлением (см. Панченков – Лебедев, стр.261, табл.27), поскольку здесь происходит пространственное разделение двух свободных валентностей; из единого центра возникают два пространственно независимых. Элементарные акты линейного обрыва (стадия 5) происходят на стенке. (На стадии 5, а далее и 6 более строго следовало бы частицы M заменить удельной поверхностью стенки S). Акты квадратичного обрыва происходят в объёме, а на стенке обрыв уже мономолекулярный (стадии 5 и 6).

Теория пределов взрыва приведена у Панченкова и Лебедева, а также у Лейдлера...

В реакционной газовой смеси (в пламени) содержится до 18% атомарного водорода. Для расчёта режимов образования и расходования этих наиболее активных частиц вводится упрощение, называемое методом полустационарных концентраций Н.Н.Семёнова, который состоит в том, что квазистационарное приближение вводится только для менее активных частиц. Концентрация наиболее активных частиц в принципе не может быть стационарной. На этой основе удаётся принципиально упростить схему её расчёта.

(9.1)

1) Цепной разветвлённый процесс есть результат суперпозиции стадий четырёх типов: зарождения, продол­жения, разветвления и обрыва. На стадии продолжения число активных центров остаётся неизменным. Поэтому желательно в уравнении 3) от неё изба­виться, и сосредоточиться на трёх основных стадиях, конкуренция которых формирует специфику именно раз­ветвлённого процесса.

2) Поскольку за разветвление ответственны наиболее активные частицы - атомарный водород, то цель преобразо­ваний состоит в том, чтобы именно его концентрацию ввести всюду в явном виде. Равенство позволяет записать: . Благодаря уравнению 2) из главного в нашей задаче уравнения 3) :

а) исключаем скорость , и б) заменяем скорость скоростью , и получаем формулу (9.2).

(9.2)

Режимы разветвлённой цепной реакции

Конкуренция разветвления и обрыва

f -скорость разветвления цепи и F - фактор разветвления,

g -скорость обрыва цепи и G - фактор обрыва:

Режимы образования и гашения активных центров n:

(9.3)

Полученное выражение предсказывает два предельных режима режима изменения концентрации активных центров, (см. рис.): а)-при доминирующем обрыве цепи система стационарно насыщается активными центрами; б)-при доминирующем разветвлении активные центры способны неограниченно накапливаться.

Эти предельные режимы цепной разветвлённой реакции следующие:

В результате конкуренции разветвления и обрыва возникает специфический механизм цепной разветвлённой реакции, зависящий от многих факторов. В книге Лейдлера (стр.194) рассматриваются взрывные пределы этой реакции. Цитируем: “Реакция водорода с кислородом протекает со скоростями, удобными для измерения между 450 и 600о С; выше этого интервала все смеси взрываются. Если стехиометрическую смесь (H>2>;O>2>) держать при (T; p)=(550 оС; 2 тор), то протекает гомогенная реакция. С постепенным повышением давления скорость реакции увеличивается. При некотором критическом давлении, величиною в несколько миллиметров (его точное значение зависит от размеров и формы реакционного сосуда), смесь взрывается. Если смесь выдерживать при p =200 тор, то вновь протекает спокойная стационарная реакция, но, если давление понизить, то при p =100 тор смесь взорвётся. Таким образом при этой температуре имеется некоторый интервал давлений, внутри которого наблюдается взрыв, а выше и ниже его реакция протекает со стационарной скоростью. Выше 600 оС смесь взрывается при всех давлениях, а ниже 400 оС не взрывается совсем. Два взрывных предела называют первым и вторым или верхним и нижним.

Существует также и третий предел при ещё более высоких давлениях. Иногда этот третий предел является просто термическим пределом; и в этих случаях скорости реакций становятся настолько высокими, что условие изотермичности не сохраняется. Такие взрывы, которые происходят за счёт повышения температуры реакционной системы, называют термическими (тепловыми) . Существуют доводы и в пользу того, что взрыв при третьем пределе в системе (H>2>;O>2>) не является термическим, а происходит за счёт внезапного повышения концентрации активных центров-свободных радикалов...”.

Заключение.

Предлагаемое пособие не учебник, а лишь краткий конспект. В русской вузовской литературе имеется превосходный пример авторского текста, не претендующего на исчерпывающую полноту изложения, но вскрывающего автор­скую репетицию перед решающим аудиторным лекционным представлением. Это блестящий «Конспект лекций по квантовой механике» великого Энрико Ферми, бывшего «собратом по цеху» и оставшегося непревзойдённым образцом для подражания. В химии, насколько мне известно, подобные попытки ещё не предпринимались ... Может быть, в наше информационно - перегруженное время опыт окажется полезным... Во всяком случае, Ваш покорный слуга старался всячески выделить и никоим образом не скрыть основные первоисточники и тех авторов, мыслями которых он беззастенчиво пользовался как своими собственными... За пределами наших возможностей вынужденно остались вопросы ферментного катализа.

К сожалению, стиль неполноты диктуется нынешними мучительными условиями преподавания в вузе вкупе с причудливыми требованиями, которые предъявляют ретивые вожди интеллектуального конвейера. Всероссийские дела на рубеже тысячелетий всё более и более напоминают известный американский роман «Бумага Мэтлока», и трудно ожидать скорого выправления положения. Всё же надежда умирает последней...

В завершение хотелось бы отвлечь читателя от сугубо профессиональной темы и вспомнить простую истину, что столпом высшего образования России всегда было гуманитарное начало. А потому в качестве эпилога можно к нему и обратиться, и предложить читателю кое-что для размышления (или для развлечения) - как хотите! ...

Вспомним только, что грозной ядерной энергетике XX века непосредственно предшествовала созданная в его первой трети в нашей стране великим Н.Н. Семёновым и его блестящими сподвижниками Я.Б. Зельдовичем и Ю.Б. Харитоном кинетика химического (да и ядерного тоже !) горения и взрыва...