Дифракция света (работа 2)
Содержание
Явление дифракция
Дифракция на щели
Дифракционная решётка
Принцип Гюйгенса – Френеля
Метод зон Френеля
Дифракция Фраунгофера одной щели
Список литературы
1. Явление дифракции
Дифракция волн заключается в огибании волнами препятствий или в отклонении волн в область геометрической тени при прохождении через отверстия при условии, что линейные размеры этих препятствий порядка или меньше длины волны. Тип волн не имеет значения: дифракция наблюдается и для звука, и для света, и для любых других волновых процессов.
Наблюдение дифракции световых волн возможно только тогда, когда размеры препятствий будут порядка 10-6-10-7 м (для видимого света). Когда размеры щели сравниваются по порядку с длиной волны, щель становится источником вторичных сферических волн, интерференция которых и определяет картину распределения интенсивности за щелью. В частности, свет проникает в геометрически недоступную область. Таким образом, в видимой области спектра наблюдать дифракцию нелегко. Для электромагнитных волн в других диапазонах дифракция наблюдается повседневно, везде и всюду, так как, если бы не это явление, мы не смогли бы, например, слушать радио в закрытых помещениях.
Согласно общепринятому определению, Дифракция света, явления, наблюдающиеся при распространении света мимо резких краёв непрозрачных или прозрачных тел, сквозь узкие отверстия. При этом происходит нарушение прямолинейности распространения света, т. е. отклонение от законов геометрической оптики. Вследствие дифракция света при освещении непрозрачных экранов точечным источником света на границе тени, где, согласно законам геометрической оптики, должен был бы происходить скачкообразный переход от тени к свету, наблюдается ряд светлых и тёмных дифракционных полос. Поскольку дифракция свойственна всякому волновому движению, открытие дифракции света в 17 в. итальянским физиком и астрономом Ф. Гримальди и её объяснение в начале 19 в. французским физиком О. Френелем явились одним из основных доказательств волновой природы света. Приближённая теория дифракция света основана на применении Гюйгенса - Френеля принципа. Для качественного рассмотрения простейших случаев дифракция света может быть применено построение зон Френеля. При прохождении света от точечного источника через небольшое круглое отверстие в непрозрачном экране или вокруг круглого непрозрачного экрана наблюдаются дифракционные полосы в виде концентрических окружностей. Если отверстие оставляет открытым чётное число зон, то в центре дифракционной картины получается тёмное пятнышко, при нечётном числе зон - светлое. В центре тени от круглого экрана, закрывающего не слишком большое число зон Френеля, получается светлое пятнышко. Принцип Гюйгенса – Френеля позволяет объяснить явление дифракции и дать методы ее количественного расчета. Различают два случая дифракции. Если преграда, на которой происходит дифракция, находится вблизи от источника света или от экрана, на котором производится наблюдение, то фронт падающих или дифрагированных волн имеет криволинейную поверхность; этот случай называется дифракцией Френеля или дифракцией в расходящихся лучах, т. е. где b - размер отверстия, z - расстояние точки наблюдения от экрана, l - длина волны (дифракция Френеля), и дифракция света в параллельных лучах, при которой отверстие много меньше одной зоны Френеля, т. е. (дифракция Фраунгофера). В последнем случае при падении параллельного пучка света на отверстие пучок становится расходящимся с углом расходимости j ~ l/b (дифракционная расходимость). Плоские волны получаются либо удалением источника света и места наблюдения от преграды, вызывающей дифракцию, либо применением соответственного расположения линз.
С точки зрения представлений геометрической оптики о прямолинейном распространении света граница тени за непрозрачным препятствием резко очерчена лучами, которые проходят мимо препятствия, касаясь его поверхности. Следовательно, явление дифракции необъяснимо с позиций геометрической оптики. По волновой теории Гюйгенса, рассматривающей каждую точку поля волны как источник вторичных волн, распространяющихся по всем направлениям, в том числе и в область геометрической тени препятствия, вообще неясно, как может возникнуть сколько-нибудь отчетливая тень. Тем не менее, опыт убеждает нас в существовании тени, но не резко очерченной, как утверждает теория прямолинейного распространения света, а с размытыми краями. Причем в области размытости наблюдается система интерференционных максимумов и минимумов освещенности
2. Дифракция на щели
Большое практическое значение имеет случай дифракция света на щели. При освещении щели параллельным пучком монохроматического света на экране получается ряд тёмных и светлых полос, быстро убывающих по интенсивности. Если свет падает перпендикулярно к плоскости щели, то полосы расположены симметрично относительно центральной полосы, а освещённость меняется вдоль экрана периодически с изменением j, обращаясь в нуль при углах j, для которых sin j = m/lb (m = 1, 2, 3 ....). При промежуточных значениях освещённость достигает максимальных значений. Главный максимум имеет место при m = 0, при этом sin j = 0, т. е. j = 0. Следующие максимумы, значительно уступающие по величине главному, соответствуют значениям j, определённым из условий: sin j = 1,43 l/b, 2,46 l/b, 3,47 l/b и т.д. С уменьшением ширины щели центральная светлая полоса расширяется, а при данной ширине щели положение минимумов и максимумов зависит от l, т. е. расстояние между полосами тем больше, чем больше l. Поэтому в случае белого света имеет место совокупность соответствующих картин для разных цветов. При этом главный максимум будет общим для всех l и представится в виде белой полоски, переходящей в цветные полосы с чередованием цветов от фиолетового к красному. Если имеются 2 идентичные параллельные щели, то они дают одинаковые накладывающиеся друг на друга дифракционные картины, вследствие чего максимумы соответственно усиливаются, а, кроме того, происходит взаимная интерференция волн от первой и второй щелей, значительно осложняющая картину. В результате минимумы будут на прежних местах, т.к. это те направления, по которым ни одна из щелей не посылает света. Кроме того, возможны направления, в которых свет, посылаемый двумя щелями, взаимно уничтожается. Таким образом, прежние минимумы определяются условиями: b sin j = l, 2l, 3l, ..., добавочные минимумы d sin j = l/2, 3l/2, 5l/2, ... (d - размер щели b вместе с непрозрачным промежутком а), главные максимумы d sin j = 0,l, 2l, 3l, ..., т. е. между двумя главными максимумами располагается один добавочный минимум, а максимумы становятся более узкими, чем при одной щели. Увеличение числа щелей делает это явление ещё более отчётливым. Дифракция света играет существенную роль при рассеянии света в мутных средах, например на пылинках, капельках тумана и т.п. На дифракция света основано действие спектральных приборов с дифракционной решёткой (дифракционных спектрометров). Дифракция света определяет предел разрешающей способности оптических приборов (телескопов, микроскопов и др.). Благодаря дифракция света изображение точечного источника (например, звезды в телескопе) имеет вид кружка с диаметром lflD, где D - диаметр объектива, а f - его фокусное расстояние. Расходимость излучения лазеров также определяется дифракция света. Для уменьшения расходимости лазерного пучка его преобразуют в более широкий пучок при помощи телескопа, и тогда расходимость излучения определяется диаметром D объектива по формуле j ~ l/D.
Дифракционная картина, наблюдаемая на экране, поставленном за перегородкой с одной щелью, может быть рассчитана на основании принципа суперпозиции и интерференции волн. Пусть на щель падает монохроматический пучок света длиной . Размеры щели d сравнимы с : d ~ . Расстояние от щели до экрана L >> d. Каждая точка щели является, согласно принципу Гюйгенса, источником вторичной сферической волны. Эти волны интерферируют между собой, так что истинное положение фронта результирующей волны является огибающей вторичных волн с учетом их интерференции. Рассмотрим наложение двух таких волн, идущих от середины щели и от одного из краев, и вычислим разность хода таких волн в произвольной точке экрана. Из простых геометрических соображений с учетом малости угла можно получить, что разность хода этих двух волн равна:
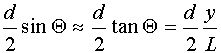
где y - координата точки наблюдения на экране. Интерференция двух волн будет деструктивной, если разность хода будет равна целому числу полуволн m(/2). Отсюда находятся координаты тех точек на экране, где возникают темные полосы:
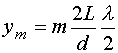
Распределение интенсивности света в дифракционной картине имеет резкий максимум. Следует отметить, что измерения положения минимумов позволяют (при известных параметрах d и L) определить длину волны света.
3. Дифракционная решетка
Более совершенным прибором, позволяющим проводить спектральный анализ света, является дифракционная решетка. Дифракционная решетка представляет собой систему большого числа одинаковых по ширине и параллельных друг другу щелей, лежащих в одной плоскости и разделенных непрозрачными промежутками, равными по ширине. Дифракционная решетка изготавливается путем нанесения параллельных штрихов на поверхность стекла с помощью делительных машин. Места, прочерченные делительной машиной, рассеивают свет во все стороны и являются, таким образом, практически непрозрачными промежутками между неповрежденными частями пластинки, которые играют роль щелей. Число штрихов на 1 мм определяется областью спектра исследуемого излучения - от 300 1/мм (в инфракрасной области) до 1200 1/мм (в ультрафиолетовой). Это устройство бывает двух типов: пропускающие (прозрачные щели, чередующиеся с непрозрачными промежутками) и отражательные (участки, отражающие свет, чередуются с участками, рассеивающими свет). И в том и в другом случае на поверхность наносится большое количество щелей или рассеивающих свет полос, причем число штрихов доходит до 103 на 1 мм, а общее число штрихов ~ 105. Расстояние между двумя соседними щелями называется периодом решетки. Две волны, идущие от краев двух соседних щелей, интерферируют конструктивно, если:
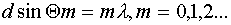
Ясно, что в этом случае волны от всех щелей будут усиливать друг друга (разность хода, определяемая точками, отстоящими друг от друга на целое число периодов решетки, не нарушает условия конструктивной интерференции), и после фокусировки всех лучей с помощью линзы на экране возникнут максимумы интенсивности. Таким образом, предыдущая формула определяет положение максимумов дифракционной картины, создаваемой дифракционной решеткой. Положение всех максимумов, кроме главного максимума, отвечающего m = 0, зависит от длины волны. Поэтому если на решетку падает белый свет, то он разлагается в спектр. С помощью дифракционной решетки можно очень точно измерять длину волны, так как при большом числе щелей области максимумов интенсивности сужаются, превращаясь в тонкие яркие полосы, а расстояния между максимумами (ширина темных полос) растут.
Наилучшим качеством обладают отражательные дифракционные решетки. Они представляют собой чередующиеся участки настолько малые, что, отражая свет, они рассеивают его вследствие дифракции. Таким образом, пучок света разбивается на множество когерентных лучей.
Если ширина прозрачных участков а, а ширина непрозрачных промежутков b, то величина d=a+b называется периодом решетки. Если на решетку нормально (перпендикулярно) к ее поверхности падает свет с длиной волны то, как следует из рисунка 1, лучи, рассеянные под углом к первоначальному направлению от соответствующих мест каждой из щелей, обладают разностями хода dsin (I и II лучи), 2dsin (I и III лучи) и т. д.
В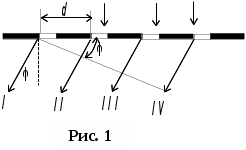
олны
усиливают друг друга при интерференции,
если эта разность хода равна целому
числу волн. Углы, под которыми наблюдаются
максимумы, находятся из соотношения
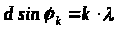 ,
k
= 0, 1,
2,
3…
(1)
,
k
= 0, 1,
2,
3…
(1)
Максимумы наблюдаются по обе стороны от падающего луча, а центральный максимум (k=0) наблюдается в направлении падающего луча.
Зеркальная поверхность лазерного компакт-диска представляет собой спиральную дорожку, шаг которой соизмерим с длиной волны видимого света. На такой упорядоченной и мелкоструктурной поверхности в отраженном свете заметно проявляются дифракционные и интерференционные явления, что и является причиной радужной окраски создаваемых им бликов. Луч лазера занимает на компакт-диске настолько малую площадь, что этот участок можно считать одномерной дифракционной решеткой.
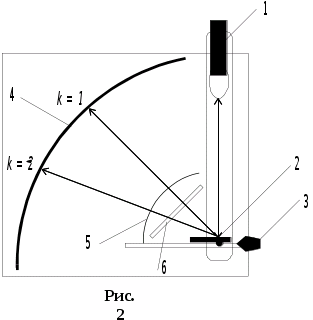
Схема прибора (прибор №1), для наблюдения дифракции света на кусочке компакт-диска, играющего роль отражательной дифракционной решетки, представлена на рисунке 2. Здесь: 1 – источник света – лазер-брелок, укрепленной на поворачивающейся планке, 2 – отражательная дифракционная решетка – кусочек компакт-диска, 3 – зажим для крепления препарата, 4 - транспортир для измерения углов дифракции, 5 – транспортир для измерения угла падения луча света, 6 – зажим для крепления поляроида.
4. Принцип Гюйгенса – Френеля
Особенность дифракционных эффектов состоит в том, что дифракционная картина в каждой точке пространства является результатом интерференции лучей от большого числа вторичных источников Гюйгенса. Объяснение этих эффектов было осуществлено Френелем и получило название принципа Гюйгенса - Френеля. Сущность принципа Гюйгенса - Френеля можно представить в виде нескольких положений:
всю волновую поверхность, возбуждаемую каким-либо источником S0 площадью S, можно разбить на малые участки с равными площадями dS, которые будут являться системой вторичных источников, испускающих вторичные волны;
эти вторичные источники, эквивалентные одному и тому же первичному источнику S0, когерентны между собой. Поэтому волны, распространяющиеся от источника S0, в любой точке пространства должны являться результатом интерференции всех вторичных волн;
мощности излучения всех вторичных источников - участков волновой поверхности с одинаковыми площадями – одинаковы;
каждый вторичный источник (с площадью dS) излучает преимущественно в направлении внешней нормали п к волновой поверхности в этой точке; амплитуда вторичных волн в направлении, составляющем с п угол , тем меньше, чем больше угол а, и равна нулю;
амплитуда вторичных волн, дошедших до данной точки пространства, зависит от расстояния вторичного источника до этой точки: чем больше расстояние, тем меньше амплитуда;
когда часть волновой поверхности S прикрыта непрозрачным экраном, вторичные волны излучаются только открытыми участками этой поверхности. При этом часть световой волны, закрытая непрозрачным экраном, не действует совсем, а открытые области волны действуют так, как если бы экрана совсем не было.
5. Метод зон Френеля
Дифракция Френеля играет основную роль в волновой теории, т.к. вопреки принципу Гюйгенса и на основе принципа Гюйгенса - Френеля, объясняет прямолинейность распространения света в свободной от препятствий однородной среде. Чтобы показать это, рассмотрим действие сферической световой волны от точечного источника s0 в произвольной точке пространства Р. Волновая поверхность такой волны симметрична относительно прямой S0P. Амплитуда искомой волны в точке Р зависит от результата интерференции вторичных волн, излучаемых всеми участками dS поверхности S. Амплитуды и начальные фазы вторичных волн зависят от расположения соответствующих источников dS по отношению к точке Р. Воспользовавшись симметрией задачи, Френель предложил оригинальный метод разбиения волновой поверхности на зоны (метод зон Френеля). По этому методу волновая поверхность разбивается на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки Р отличаются на (длина световой волны в той среде, в которой распространяется волна). Если обозначить через r0 расстояние от вершины волновой поверхности О до точки Р, то расстояния r0 + k образуют границы всех зон, где k - номер зоны. Колебания, приходящие в точку Р от аналогичных точек- двух соседних зон, противоположны по фазе, так как разность хода от этих зон до точки Р равна . Поэтому при наложении эти колебания взаимно ослабляют друг друга, и результирующая амплитуда выразится суммой:
А=А1-А2+А3-А4+….
Величина амплитуды ак зависит от площади – й зоны и угла между внешней нормалью к поверхности зоны в любой ее точке и прямой, направленной из этой точки в точку Р. Можно показать, что площадь - й зоны не зависит от номера зоны в условиях. Таким образом, в рассматриваемом приближении площади всех зон Френеля равновелики и мощность излучения всех зон Френеля – вторичных источников - одинакова. Вместе с тем, с увеличением k возрастает угол между нормалью к поверхности и направлением в точку Р, что приводит к уменьшению интенсивности излучения k-й зоны в данном направлении, т.е. к уменьшению амплитуды Ak по сравнению с амплитудами предыдущих зон. Амплитуда Ak уменьшается также вследствие - увеличения расстояния от зоны до точки Р с ростом k. В итоге
A1 > A2 > A3 > A4 > ... > Ak>….
Вследствие большого числа зон убывание Ak носит монотонный характер и приближенно можно считать, что с учетом малости амплитуды удаленных зон, все выражения в скобках равны нулю. Полученный результат означает, что колебания, вызываемые в точке Р сферической волновой поверхностью, имеют такую же амплитуду, как если бы действовала только половина центральной зоны Френеля. Следовательно, свет от источника S0 в точку Р распространяется как бы в пределах очень узкого прямого канала, т.е. прямолинейно. Мы приходим к выводу, что в результате явления интерференции уничтожается действие всех зон, кроме первой.
6. Дифракция Фраунгофера одной щели
Практически щель представляется прямоугольным отверстием, длина которого значительно больше ширины. В этом случае свет дифрагирует вправо и влево от щели. Если наблюдать изображение источника в направлении, перпендикулярном направлению образующей щели, то можно ограничиться рассмотрением дифракционной картины в одном измерении (вдоль х). Бели волна падает нормально к плоскости щели, в соответствии с принципом Гюйгенса - Френеля, точки щели являются вторичными источниками волн, колеблющимися в одной фазе, так как плоскость щели совпадает с фронтом падающей волны. Разобьем площадь щели на ряд узких полосок равной ширины, параллельных образующей щели. Фазы волн от разных полосок на одинаковых расстояниях, в силу вышесказанного, равны, амплитуды также равны, т.к. выбранные элементы имеют равные площади и одинаково наклонены к направлению наблюдения.
Если бы при прохождении света через щель соблюдался закон прямолинейного распространения света (не было бы дифракции), то на экране Э, установленном в фокальной плоскости линзы L2 получалось бы изображение щели. Следовательно, направление = 0 определяет недифрагированную волну с амплитудой a0, равной амплитуде волны, посылаемой всей щелью.
Вследствие дифракции световые лучи отклоняются от прямолинейного распространения на углы. Отклонение вправо и влево симметрично относительно осевой линии ОС0 (рис. 8.5, С и С,). Для отыскания действия всей щели в направлении, определяемом углом, необходимо учесть разность фаз, характеризующую волны, доходящие до точки наблюдения С от различных полосок (зон Френеля), т.к. как указывалось выше, в побочном фокусе линзы С собираются все параллельные лучи, падающие на линзу под углом к ее оптической оси ОС0, перпендикулярной фронту падающей волны. Проведем плоскость FD, перпендикулярную к направлению дифрагированных лучей и представляющую фронт новой волны. Так как линза не вносит дополнительной разности хода лучей, ход всех лучей от плоскости FD до точки С одинаков. Следовательно, полная разность хода лучей от щели FE задается отрезком ED. Проведем плоскости, параллельные волновой поверхности FD, таким образом, чтобы они разделили отрезок ED на несколько участков, каждый из которых имеет длину /2. Эти плоскости разделят щель на вышеупомянутые полоски - зоны Френеля, причем разность хода от соседних зон равна в соответствии с методом Френеля. Тогда результат дифракции в точке C определится числом зон Френеля, укладывающихся в щели: если число зон четное (z = 2k), в точке С наблюдается минимум дифракции, если z - нечетное (z = 2k+1), в точке С - максимум дифракции. Число зон Френеля, укладывающихся на щели FE, определяется тем, сколько раз в отрезке ED содержится, т.е. z = 0. Отрезок ED, выраженный через ширину щели и угол дифракции, запишется как ED = 0. В итоге для положения максимумов дифракции получаем условие, где k - 1,2,3.. - целые числа. Величина k, принимающая значения чисел натурального ряда, называется порядком дифракционного максимума. Знаки + и - в формулах соответствуют лучам света, дифрагирующим от щели под углами + и - и собирающимся в побочных фокусах линзы L2: C и C, симметричных относительно главного фокуса С0. В направлении = 0 наблюдается самый интенсивный центральный максимум нулевого порядка, т.к. колебания от всех зон Френеля приходят в точку С0 в одной фазе. Положение центрального максимума (= 0) не зависит от длины волны и, следовательно, является общим для всех длин волн. Поэтому в случае белого света центр дифракционной картины представится в виде белой полоски. Ясно, что положение максимумов и минимумов зависит от длины волны. Поэтому простое чередование темных и светлых полос имеет место только при монохроматическом свете. В случае белого света дифракционные картины для волн с разными сдвигаются в соответствии с длиной волны. Центральный максимум белого цвета имеет радужную окраску только по краям (на ширине щели укладывается одна зона Френеля). Боковые максимумы для разных длин волн уже не совпадают между собой; ближе к центру располагаются максимумы, соответствующие более коротким волнам. Длинноволновые максимумы отстоят друг от друга дальше, чем коротковолновые. Поэтому дифракционный максимум представляет собой спектр, обращенный к центру фиолетовой частью. Полное гашение света не происходит ни в одной точке экрана, так как максимумы и минимумы света с разными перекрываются.
Список литературы
1. Горелик Г. С., Колебания и волны. М., 2000.
2. Дягилев Ф.М. Из истории физики и жизни ее творцов. М., 1996.
3. Киттель Ч.М. Введение в физику. М., 1998.
4. Ландсберг Г. С., Оптика (Общий курс физики, т. 3). М., 1997.
5. Савельев, Трофимов Курс физики, т.3. М., 1989.
6. Спасский Б.И. Физика в ее развитии. М., 1999.
7. Эйген М. , Шустер П. Большой энциклопедический словарь. М., 2005.