Конструирование и расчет балочной клетки и колонны при проектировании рабочей площадки производственного здания

Курсовая работа

«Конструирование и расчет балочной клетки и колонны при проектировании рабочей площадки производственного здания»

Содержание

1. Компоновка балочной клетки и выбор стали

2. Нормальный тип балочной клетки

2.1 Расчет железобетонного настила

2.2 Расчет балки настила

3. Усложненный тип балочной клетки

3.1 Расчет балки настила

3.2 Расчет вспомогательной балки

4. Выбор оптимального варианта балочной клетки

5. Расчет главной балки

5.1 Определение усилий

5.2 Компоновка сечения

5.3 Проверка прочности принятого сечения балки

5.4 Изменение сечения балки по длине

5.5 Проверка общей устойчивости балки

5.6 Проверка местной устойчивости элементов балки

5.7 Проверка жесткости главной балки

5.8 Расчет соединения пояса со стенкой

5.9 Конструирование и расчет опорной части главной балки

5.10 Проектирование монтажного стыка главной балки

6. Расчет колонн

6.1 Расчет колонны на устойчивость относительно материальной оси x–x

6.2 Расчет колонны на устойчивость относительно свободной оси y-y

6.3 Расчет планок

6.4 Конструирование и расчет оголовка сквозной колонны

6.5 Конструирование и расчет базы колонны

Список литературы

1. Компоновка балочной клетки и выбор стали

Исходные данные приняты по заданию.

В рабочих площадках применяют нормальный и усложненный тип балочных клеток. Нормальный тип включает главные балки и опирающиеся на них балки настила, непосредственно поддерживающие настил. В усложненном типе добавляются вспомогательные балки, укладываемые на главные, на них опираются балки настила и настил. В качестве настила используются железобетонные плиты.

Выбор класса стали производится по СНиП [1, табл. 50*], Ry выбирается по [1, табл. 51*]. Выбираю сталь С 255, с расчетным сопротивлением Ry = 240 МПа.

2. Нормальный тип балочной клетки

Настил – железобетонный.

Балки настила с шагом а1 = 1,5 м.

Рис. 1. Нормальный тип балочной клетки

2.1 Расчет железобетонного настила

При использовании в качестве несущего настила железобетонных плит их толщину принимаем расчетного пролета плиты lн и полезной нормативной нагрузки pn

Расчетный пролет настила, равный шагу балок настила lн = а1 = 1,5 м.

При нормативной полезной нагрузке pn = 20 кН/м2, принимаем толщину плиты tпл = 10 см. Нормативная нагрузка от веса железобетонной плиты (при плотности железобетона )

2.2 Расчет балки настила

Определяем нормативные и расчетные нагрузки.

Нормативная нагрузка на балку принимается равномерно распределенной

Расчетная нагрузка

где g = 1,1 – коэффициент надежности по нагрузке для постоянной нагрузки от железобетонных плит.

Рис. 2. Расчетная схема балки настила

Нормативный изгибающий момент

Расчетный изгибающий момент

Максимальная поперечная сила

Требуемый момент сопротивления поперечного сечения балки при работе с учетом упругопластических деформаций

По сортаменту принимаем I 50Б2, имеющий ближайший больший момент сопротивления статический момент полусечения Sx = 970,2 см3; момент инерции сечения Ix = 42390 см4; площадь сечения А = 102,8 см2; ширина пояса bf = 200 мм; толщина пояса tf = 14 мм;

Уточняем коэффициент с1, M и Q c учетом собственного веса балки настила

Площадь пояса

Площадь стенки

Отношение

По табл. определяем коэффициент с1 = 1,11.

Равномерно распределенная нагрузка от собственного веса балки настила длиной 1 м

Нормативная нагрузка на балку настила с учетом собственного веса

Расчетная нагрузка с учетом собственного веса

Нормативный изгибающий момент с учетом собственного веса

Расчетный изгибающий момент с учетом собственного веса

Проверяем принятое сечение.

Проверка прочности

Проверка жесткости

где fu = l/208 = 4,33 см при пролете l = 9 м.

Принятое сечение удовлетворяет условиям прочности и жесткости.

Определяем вес балки настила на 1м2 рабочей площадки

3. Усложненный тип балочной клетки

Настил – железобетонный.

Балки настила с шагом а1 = 1,5 м.

Вспомогательные балки с шагом а2 = 5 м.

Рис. 3. Усложненный тип балочной клетки

3.1 Расчет балки настила

Толщина настила при шаге а1=1,5 м принимается как в нормальном типе балочной клетки (tн = 10 мм).

Пролет балки настила .

Нормативная и расчетная нагрузки на балку настила принимаются как в нормальном типе балочной клетки: qn = 33,75 кН/м; q = 40,125 кН/м.

Рис. 4. Расчетная схема балки настила

Нормативный изгибающий момент

Расчетный изгибающий момент

Максимальная поперечная сила

По сортаменту принимаем I 35Б1, имеющий ближайший больший момент сопротивления статический момент полусечения Sx = 328,6 см3; момент инерции сечения Ix = 10060 см4; площадь сечения А = 49,53 см2; ширина пояса bf = 155 мм; толщина пояса tf = 8,5 мм;

Уточняем коэффициент с1, M и Q c учетом собственного веса балки настила

Площадь пояса

Площадь стенки

Отношение

По табл. определяем коэффициент с1 = 1,1132.

Равномерно распределенная нагрузка от собственного веса балки настила длиной 1 м

Нормативная нагрузка на балку настила с учетом собственного веса

Расчетная нагрузка с учетом собственного веса

Нормативный изгибающий момент с учетом собственного веса

Расчетный изгибающий момент с учетом собственного веса

Проверяем принятое сечение.

Проверка прочности

Проверка жесткости

где fu = l/183 = 2,73 см при пролете l = 5 м.

Принятое сечение удовлетворяет условиям прочности и жесткости.

Определяем вес балки настила на 1м2 рабочей площадки

3.2 Расчет вспомогательной балки

Пролет вспомогательной балки l = 9 м.

Нагрузка на вспомогательную балку передается от балок настила в виде равномерно распределенной.

Рис. 5. Расчетная схема вспомогательной балки

Нормативная нагрузка на вспомогательную балку

Расчетная нагрузка

Нормативный изгибающий момент

Расчетный изгибающий момент

Требуемый момент сопротивления

По сортаменту принимаем I 90Б1, имеющий ближайший больший момент сопротивления статический момент полусечения Sx = 3964 см3; момент инерции сечения Ix = 304400 см4; площадь сечения А = 247,1 см2; ширина пояса bf = 300 мм; толщина пояса tf = 18,5 мм;

Равномерно распределенная нагрузка от собственного веса вспомогательной балки длиной 1 м

Нормативная нагрузка на балку настила с учетом собственного веса

Расчетная нагрузка с учетом собственного веса

Нормативный изгибающий момент с учетом собственного веса

Расчетный изгибающий момент с учетом собственного веса

Проверяем принятое сечение.

Проверка прочности

Проверка жесткости

где fu = l/208 = 4,33 см при пролете l =9 м.

Принятое сечение удовлетворяет условиям прочности и жесткости.

Определяем вес вспомогательной балки на 1м2 рабочей площадки

4. Выбор оптимального варианта балочной клетки

Необходимо сравнить два варианта балочных клеток. Сравнение производится по расходу материала, а также по количеству балок, определяющему трудоемкость монтажа и стоимость перевозки. К дальнейшей разработке принимается наиболее рациональный вариант.

Анализ вариантов по показателям, представленных в табл. 1.

Таблица 1. Сравнение вариантов балочной клетки (расход на 1 м2 рабочей площадки)

Наименование элемента	Нормальный тип	Усложненный тип
Расход железобетона, м3/м2	Расход стали, кг/м2	Стоимость, руб./м2	Коли-чество балок	Расход железобетона, м3/м2	Расход стали, кг/м2	Стои- мость руб./м2	Ко- ли- чест- во ба- лок
Настил	0,1				0,1
Балки настила		53,8		63		25,9		126
Вспомогательные балки		–
Суммарный расход стали		53,8				38,8		21
Суммарный расход железобетона	0,1				0,1

Принимаем к дальнейшей разработке нормальный тип балочной клетки:

– настил железобетонный, толщиной tн = 10 см;

– балки настила стальные с шагом а1 = 1,5 м.

5. Расчет главной балки

Сечение сварной балки двутавровое симметричное, составленное из трех металлопрокатных листов. Выбираю сталь С 345, с расчетным сопротивлением Ry = 300 МПа (толщина проката 20÷40 мм).

5.1 Определение усилий

При частом расположении балок настила (шаг а1 = 1,5 м < l/5 = 15/5 = 3 м) сосредоточенную нагрузку, передаваемую на главную балку от балок настила, заменяем равномерно распределенной нагрузкой.

Расчетная схема главной балки представлена на рис.5.

Рис. 6. Расчетная схема главной балки

Нормативная нагрузка

Расчетная нагрузка

где b = 9 м – шаг главных балок.

Расчетный изгибающий момент в середине пролета

Нормативный изгибающий момент

Расчетная поперечная сила в опорном сечении

5.2Компоновка сечения

Рис. 7. Сечение главной балки

Балку рассчитываем в упругой стадии работы. Из условия прочности требуемый момент сопротивления балки

где Ry = 300 МПа при толщине проката более 20 мм;

Назначаем высоту сечения балки h, которая определяется максимально допустимым прогибом балки, связанным с жесткостью балки, экономическими соображениями и строительной высотой перекрытия Н, т.е. разностью отметок верха настила и верха габарита помещения под рабочей площадкой. Минимальная высота из условия жесткости

где fu = l/225 = 0,0044 при пролете l = 15 м – предельный прогиб главной балки.

Высота разрезной главной балки принимается в пределах (1/10…1/13)l = =(1,5…1,15 м). Предварительно принимаем высоту балки h = 1,5 м.

Оптимальная высота балки из условия наименьшего расхода стали

здесь tw – толщина стенки балки, предварительно определяемая по эмпирической зависимости tw = 7 + 3h/1000 = 7 + 3·1500/1000 = 11,5 мм.

Принимаем tw = 12 мм.

Максимально возможная высота балки

hстр = H – (tн + hбн + Δ) = (1080 –800) – (10 + 49,6 + 14) = 206,4 см,
где Δ= fu + (30 …100 мм) = 6,67 + 7,33 = 14 см – размер, учитывающий предельный прогиб балки fu = 6,67 см и выступающие части, расположенные ниже нижнего пояса балки (толщина стыковых накладок, болты, элементы связей т.п.).

Требуемая площадь пояса

Ширина пояса bf = h/3 = 150/3 = 50 см.

Толщина пояса tf = / bf = 115,23/50 = 2,3 см.

Сравнивая полученные данные, окончательно назначаем высоту балки h = 1550 мм. Приняв толщину поясов tf = 25 мм, ширину поясов bf = 530 мм, стенку выполняем из листовой горячекатаной стали по ГОСТ 19903–74 высотой hw = 1500 мм и толщиной tw = 12 мм.

Проверяем необходимость постановки продольных ребер жесткости. Условная гибкость стенки

следовательно, продольные ребра жесткости не требуются.

Проверяем местную устойчивость сжатого пояса, для чего отношение свеса пояса = (530–12)/2 = 259 мм к его толщине tf должно быть не более предельного, определяемого по СНиП [1],

Условие выполняется.

5.3 Проверка прочности принятого сечения балки

По назначенным размерам вычисляем фактические геометрические характеристики сечения:

– момент инерции

– момент сопротивления

– площадь сечения

По найденной площади A и плотности стального проката ρ = 7850 кг/м3 определяем вес 1 пог. м балки

где k = 1,1 – конструктивный коэффициент, учитывающий увеличение веса балки за счет ребер жесткости, накладок и т.п.

Уточняем расчетные значения изгибающего момента M и поперечной силы Q с учетом собственного веса главной балки, для этого определяем:

– нормативную нагрузку

расчетную нагрузку

– расчетный изгибающий момент

– нормативный изгибающий момент

– поперечную силу

Проверка прочности балки по нормальным напряжениям

Недонапряжение в балке составляет

что допустимо в составном сечении согласно СНиП [1].

Прочность балки обеспечена.

5.4 Изменение сечения балки по длине

Сечение составной балки, подобранное по максимальному изгибающему моменту в середине пролета, можно уменьшить в местах снижения моментов. Наибольший эффект дает симметричное изменение сечения на расстоянии x = l/6 от опор. Наиболее простым является изменение сечения за счет уменьшения ширины пояса (рис.7).

Рис. 8. Изменение сечения балки по длине

Стыкуем сжатый и растянутый пояса прямым сварным швом с выводом концов шва на подкладки с применением полуавтоматической сварки без использования физических способов контроля качества швов. Расчетное сопротивление таких сварных соединений при растяжении принимается пониженным

Для снижения концентрации напряжений при сварке встык элементов разной ширины на элементе большей ширины делаем скосы с уклоном 1:5. Определяем расчетный момент и перерезывающую силу на расстоянии

Определяем требуемые:

–момент сопротивления измененного сечения, исходя из прочности сварного стыкового шва, работающего на растяжение,

Требуемая площадь пояса

Толщина пояса bf1 = / tf = 74,08/2,5 = 29,63 см.

По конструктивным требования ширина пояса должна отвечать условиям:

–

По сортаменту принимаем измененный пояс из универсальной стали сечением 30025 мм, площадью

Вычисляем геометрические характеристики измененного сечения:

– момент инерции

– момент сопротивления

– статический момент пояса относительно нейтральной оси х-х

– статический момент половины сечения относительно оси х-х

Производим проверку прочности балки в месте изменения ее сечения в краевом участке стенки на уровне поясных швов на наиболее неблагоприятное совместное действие нормальных и касательных напряжений, для чего определяем:

Рис. 9. К проверке прочности балки

– нормальные напряжения

– касательные напряжения

– приведенные напряжения

где 1,15 – коэффициент, учитывающий локальное развитие пластических деформаций в стенке балки.

Проверка прочности на срез по касательным напряжениям

Прочность балки обеспечена.

5.5 Проверка общей устойчивости балки

Общая устойчивость балки считается обеспеченной при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный, а также, если соблюдается условие: отношение расчетной длины балки lef к ширине сжатого пояса bf не превышает критическое, определяемое по формуле

где lef = 1,5 м – расстояние между точками закрепления сжатого пояса от поперечных смещений, равное шагу балок настила a1.

В середине пролета балки

В месте уменьшения сечения балки

Устойчивость балки обеспечена.

5.6 Проверка местной устойчивости элементов балки

5.6.1. Проверка местной устойчивости сжатого пояса не требуется, так как она была обеспечена надлежащим выбором отношения свеса пояса к толщине (см.п.5.2).

5.6.2. Проверка местной устойчивости стенки балки

Определяем условную гибкость стенки

следовательно, поперечные ребра жесткости необходимы. Расстояние между основными поперечными ребрами a не должно превышать 2hw при w > 3,2. Расстояние между ребрами назначаем , что увязывается с шагом балок настила.

Рис. 10. Схема балки, укрепленная поперечными ребрами жесткости

Ширина выступающей части парного ребра

Толщина ребра

Принимаем ребро жесткости из полосовой стали 907 мм. Ребра жесткости привариваются к стенке непрерывными угловыми швами минимальной толщины. Торцы ребер должны имеют скосы с размерами 3030 мм.

Т.к. , то требуется проверка стенки на местную устойчивость.

Проверяем местную устойчивость стенки в среднем отсеке (рис.11).

Так как а = 3 м > hw = 1,5 м, определяем Mср и Qср по середине условного отсека шириной, равной половине высоты стенки hw, для чего вычисляем величины моментов и поперечных сил в середине расчетного участка (хср = 6,75 м) :

Рис. 11. К проверке местной устойчивости стенки в среднем отсеке

Краевое напряжение сжатия в стенке

Среднее касательное напряжение в отсеке

Критическое нормальное напряжение

где cсr – коэффициент, определяемый по [1, табл.21] в зависимости от значения коэффициента

который учитывает степень упругого защемления стенки в поясах;

Коэффициент cсr = 33,6614 (определен линейной интерполяцией).

Критическое касательное напряжение определяется по формуле

где здесь d – меньшая из сторон отсека

следовательно,

– отношение большей стороны отсека к меньшей.

Рис. 12. Поэтажное сопряжение балок

где F– расчетное значение сосредоточенной силы, при поэтажном сопряжении балок равное двум реакциям от балок настила F=2Qmax=2·184,374=368,75 кН; условная длина распределения сосредоточенной нагрузки (b = 200 мм – ширина пояса балки настила; tf = 25 мм – толщина верхнего пояса главной балки).

При принятом шаге поперечных ребер жесткости а = 3 м, отношение

Отношение – предельного значения, определенного при и линейной интерполяцией по [1, табл.24].

Локальное критическое напряжение

где с1 = 58,3 – коэффициент, определенный по [1, табл.23] в зависимости от δ;

Проверяем местную устойчивость стенки

Стенка устойчива.

5.7 Проверка жесткости главной балки

При равномерно распределенной нагрузке на балку

где α = 1,03 – коэффициент, учитывающий увеличение прогиба балки за счет уменьшения ее жесткости у опор, вызванного изменением сечения балки по длине.

5.8 Расчет соединения пояса со стенкой

Соединение выполняется автоматической сваркой угловыми непрерывными швами одинаковой толщины по всей длине балки.

Сравниваем

Поясные швы при рассчитываются по металлу шва по формуле

где –усилие на единицу длины шва (1 см) от поперечной силы Qmax на опоре, сдвигающее пояс относительно стенки;

Sf – статический момент пояса относительно нейтральной оси;

– при расчете по металлу шва;

βz = 1,15 – при расчете по металлу границы сплавления;

и – коэффициенты условий работы шва, равные 1;

– расчетное сопротивление сварного соединения при расчете по металлу шва, принимаемое по [1,табл. 56*] в зависимости от марки сварочной проволоки, которую выбирают по [1,табл. 55*] для автоматической сварки стали принятого класса;

– расчетное сопротивление сварного соединения при расчете по границе сплавления;

– нормативное сопротивление основного металла, принимаемое по [1,табл.51*].

Определяем требуемый катет сварного шва

Согласно [1,табл.38*] при толщине более толстого из свариваемых элементов tf = 25 мм конструктивно принимаем минимальный катет шва для автоматической сварки

5.9 Конструирование и расчет опорной части главной балки

Передача нагрузки от главной балки, установленной сверху на колонну, осуществляется через торцевое опорное ребро. Торец ребра рассчитывается на смятие, для чего он острагивается. Выступающая часть а не должна быть больше 1,5th (рис. 13) и принимается 20 мм.

Рис. 13. К расчету опорной части балки

Опорная реакция

Определяем площадь смятия торца ребра

где – расчетное сопротивление торцевой поверхности принимается по [1,табл.51*].

Принимая ширину ребра, равной ширине пояса балки у опоры определяем толщину ребра

По конструктивным соображениям рекомендуется толщину опорного ребра принимать .

Принимаем опорное ребро из листа 30016 мм с площадью Ah = 48 см2.

Местная устойчивость ребра проверяется по формуле

Ребро устойчиво.

Опорная часть главной балки из своей плоскости (относительно оси z-z) проверяется на устойчивость как условная центрально-сжатая стойка с расчетной длиной . Расчетное сечение включает в себя площадь опорного ребра Ah и площадь устойчивого участка стенки, примыкающего к ребру, шириной

Определяем площадь стойки

Момент инерции

Радиус инерции

Гибкость

По формуле 8 [1] φ = 0,959 – коэффициент продольного изгиба

Условие устойчивости центрально-сжатой стойки

Опорная часть балки устойчива.

5.10 Проектирование монтажного стыка главной балки

5.10.1. Монтажный стык на сварке

Рис. 14. Монтажный стык главной балки на сварке

Стык элементов балки осуществляется стыковыми швами. Расчетные сопротивления сварных соединений для любого вида сварки принимаются: при сжатии соединения независимо от методов контроля качества швов Rwy = Ry; при растяжении и изгибе с физическим контролем качества швов – Rwy = Ry, непроверенного физическими методами контроля – Rwy = 0,85Ry.

На монтаже физические способы контроля затруднены, поэтому расчет растянутого стыкового соединения производится по его пониженному расчетному сопротивлению. Сжатый верхний пояс и стенка соединяются прямым швом, растянутый пояс – косым швом для увеличения длины шва, так как действительное напряжение в поясе σ превышает Rwy.

Для обеспечения качественного соединения при ручной сварке, сваривая элементы толщиной более 10 мм, производится V-образная разделка кромок.

Для уменьшения сварочных напряжений соблюдается определенный порядок сварки (на рис.14 показанный цифрами): сначала свариваются поперечные стыковые швы стенки и поясов, имеющие наибольшую усадку, последними завариваются угловыми швами, имеющими небольшую продольную усадку, участки длиной по 500 мм, оставленные незаверенными на заводе. Это позволяет при монтаже совместить торцы свариваемых элементов отправочных марок, имеющих отклонение в размерах в пределах технологических допусков, и дает возможность поясным листам несколько вытянуться при усадке поперечных швов. Для ручной сварки монтажных стыков применяются электроды Э50.

5.10.2 Монтажный стык на высокопрочных болтах

Монтажные стыки на высокопрочных болтах выполняются с накладками: по три на каждом поясе и по две на стенке (рис.15).

Стык осуществляем высокопрочными болтами db = 20 мм из стали 40Х «селект», имеющей наименьшее временное сопротивление .

Способ регулирования натяжения высокопрочных болтов принимаем по M (моменту закручивания). Расчетное усилие Qbh, которое может быть воспринято каждой поверхностью трения соединяемых элементов, стянутых одним высокопрочным болтом, определяется по формуле

где – расчетное сопротивление растяжению высокопрочного болта;

– площадь сечения нетто болта db = 20 мм.

– коэффициент трения, принимаемый в зависимости от обработки поверхности по [1,табл.36*] (принят газопламенный способ обработки поверхностей);

– коэффициент надежности, принимаемый при статической нагрузке и разности номинальных диаметров отверстий и болтов с использованием регулирования натяжения болтов по М при газопламенном способе обработки поверхностей;

b – коэффициент условий работы соединения, зависящий от количества болтов n, необходимых для восприятия расчетного усилия, и принимаемый равным 1,0 при n  10.

Определяем

Расчёт стыков поясов и стенки производим раздельно. Приравнивая кривизну балки в целом , где  – радиус кривизны, кривизне ее составляющих: стенки Mw /(EIw) и поясов Mf /(EIf), находим изгибающие моменты в стенке Mw и поясах Mf, которые распределяются пропорционально их жесткостям, соответственно EIw и ЕIf. Момент инерции стенки момент инерции поясов

Изгибающий момент в стенке

Изгибающий момент в поясах

Расчет стыка пояса. Расчетное усилие в поясе определяется по формуле

Количество болтов n на каждую сторону от центра стыка балки для прикрепления накладок пояса определяем по формуле

где ks = 2 – количество поверхностей трения соединяемых элементов.

Принимаем 28 болтов и размещаем их согласно рис.15.

Диаметр отверстия d под болт делается на 3 мм больше db. Назначаем отверстие d = 23 мм.

Минимальное расстояние между центрами болтов (шаг болтов) аmin в расчетных соединениях определяется условиями прочности основного металла, принимается в любом направлении равным amin = 2,5d = 2,5·23 = 57,5 мм.

Принимаем а = 60 мм.

Рис. 15. Монтажный стык главной балки на высокопрочных болтах

Максимальное расстояние между болтами определяется устойчивостью сжатых частей элементов в промежутках между болтами (в крайних рядах при отсутствии окаймляющих уголков amax ≤ 12t = 12*14 = 168 мм, где t – толщина наиболее тонкого наружного элемента), и условием плотности соединения

Минимальное расстояние от центра болта до края элемента для высокопрочных болтов в любом направлении усилия

Принимаем с = 50 мм.

Ширина верхней накладки пояса bnf принимается равной ширине пояса

bf = 530 мм; ширина каждой нижней накладки пояса

Требуемая площадь сечения накладки определится

Толщина каждой накладки пояса определяется

Принимаем верхнюю накладку из листа 68053014 мм площадью сечения Аnf = 74,2 см2; и две нижних из листа 68023014 мм с площадью сечения

Суммарная площадь накладок

Горизонтальные болты располагаем в 6 рядов на одной полунакладке.

Две вертикальные накладки, перекрывающие стенку балки, по длине (высоте) выполняются с учетом расстояния между краем накладки и поясом, которое включает в себя толщину горизонтальных поясных накладок tnf и конструктивный зазор  = 6…15 мм

Толщина одной вертикальной накладки tnw принимаем равной толщине стенки tw за вычетом 2 мм. tnw = 10 мм.

Максимальное расстояние между крайними горизонтальными рядами болтов с учетом с = 50 мм

Расчет стыка стенки. Расчетный момент, приходящийся на стенку, уравновешивается суммой внутренних пар усилий, действующих на болты. Максимальное горизонтальное усилие Nmax от изгибающего момента, действующее на каждый крайний наиболее напряженный болт, не должно быть больше несущей способности Qbh.

Условие прочности соединения

где ai – соответствующие расстояния между парами сил, возникающих в болтах (рис.14);

m – число вертикальных рядов болтов на полунакладке.

Для определения числа рядов болтов по вертикали k и назначения их шага а вычисляем коэффициент стыка

Находим число рядов при  = 2,19 по таблице.

Принимаем k = 11 и  = 2,2  2,19.

Определяем шаг болтов по вертикали

Необходимо увеличивать количество болтов в одном вертикальном ряду, т.к. а = 136 мм > 12tnw = 120 мм. Принимаю k = 13,

Шаг a округляется до 5 мм и он укладывается целое число раз в расстоянии между крайними рядами болтов amax. Окончательно принимаем 13 рядов болтов по высоте с шагом а = 115 мм.

Проверяем стык стенки

Условие выполняется.

6. Расчет колонн

Рассчитываются центрально-сжатые сквозные колонны. Стержень сквозной колонны состоит из двух ветвей (прокатных двутавров), связанных между собой соединительной решеткой в виде планок, которые обеспечивают совместную работу ветвей.

6.1 Расчет колонны на устойчивость относительно материальной оси x–x

где lгеом – геометрическая длина колонны от фундамента до низа главной балки, равная отметке настила рабочей площадки за вычетом фактической строительной высоты перекрытия, состоящей из высоты главной балки на опоре ho, высоты балок настила hбн и толщины настила tн, плюс заглубление базы колонны ниже отметки чистого пола, принимаемое 0,6м,

Коэффициент μх = 1 (принята расчетная схема «шарнир-шарнир»)

Предварительно задались λx = 80, и определили φ = 0,686 по [1,табл.72].

Определяем требуемую площадь сечения одной ветви:

По Атр принимаю по сортаменту два двутавра I 55Б2 имеющих следующие характеристики:

Ab = 124,75 см2; A = 2Ab = 124,752 = 249,5 см2; ix = 22,43 см; iy1 = 4,7 см; Ix = 62790 см4;I y1 = 2760 см4;линейная плотность (масса 1пог.м) равна 97,9 кг/м; высота сечения Н = 54,7 см; толщина стенки d = 10 мм, ширина полки bb = 220 мм.

Проверяем устойчивость колонны относительно материальной оси, для чего определяем

и по λx определяем

где с = 1 – коэффициент условий работы по [1,табл.6].

Предельная гибкость колонны

где

– коэффициент, учитывающий недонапряжение колонны.

Условие выполняется.

6.2 Расчет колонны на устойчивость относительно свободной оси y-y

Коэффициент μy = 2 (принята расчетная схема «консоль»)

Подбор сечения колонн относительно оси y-y производится из условия ее равноустойчивости (равенства гибкости λx относительно x-x и приведенной гибкости λef относительно оси y-y), которое достигается за счет изменения расстояния между ветвями bo.

Приведенная гибкость ef определяется по [1,табл.7] для колонны с планками

при и

при

где – теоретическая гибкость стержня колонны относительно оси y-y;

– гибкость ветви колонны относительно оси 1-1;

– момент инерции сечения одной планки относительно

собственной оси z-z;

Iy1 – момент инерции ветви относительно оси 1-1 (по сортаменту);

lb – расстояние между планками по центрам тяжести;

lob– расстояние между планками в свету;

bo– расстояние между центрами тяжести ветвей колонны;

– отношение погонных жесткостей ветви и планки;

A – площадь сечения всего стержня колонны;

Приравнивая находим требуемое значение гибкости относительно свободной оси

где 1 = 35 – предварительно принятая гибкость ветви.

По λy находим радиус инерции

Воспользовавшись приближенными значениями радиусов инерции по [6,табл.11], определяем ширину сечения

Принимаем b = 920 мм и b0 = b = 920 мм, b0 – расстояние между центрами тяжести ветвей.

Расстояние в свету между полками двутавров

Расстояние между ветвями увеличивать не требуется.

Проверка колонны на устойчивость относительно оси у-у.

До проверки устойчивости колонны нужно скомпоновать сечение стержня, установить расстояние между планками, запроектировать планки, определить их размеры.

Расчетная длина ветви

Принимаем расстояние в свету между планками lob = 160 см.

Длина планки bпл принимается равной расстоянию в свету между ветвями плюс напуск на ветви по 25 мм

Высоту планок hпл устанавливают в пределах (0,5…0,8)b=475…736 мм, где b = 920 мм – ширина сечения. Принимаем hпл = 500 мм.

Толщина планок принимается по условиям местной устойчивости и должна быть

Окончательно принимаем планку из листа 75050018 мм.

Момент инерции стержня относительно оси у-у

Радиус инерции

Гибкость

Для вычисления приведенной гибкости λef относительно свободной оси проверяется отношение погонных жесткостей планки и ветви

где

Приведенная гибкость

По [1,табл.72] в зависимости от ef находим коэффициент продольного изгиба  = 0,775.

Производим проверку

Устойчивость обеспечена.

Недонапряжение составило

Условие не выполняется.

Поэтому принимаю по сортаменту два двутавра I 50Б1 имеющих следующие характеристики:

Ab = 92,98 см2; A = 2Ab = 92,982 = 185,96 см2; ix = 20 см; iy1 = 4,16 см; Ix = 37160 см4;I y1 = 1606 см4;линейная плотность (масса 1пог.м) равна 73 кг/м; высота сечения Н = 49,2 см; толщина стенки d = 8,8 мм, ширина полки bb = 200 мм.

Проверяем устойчивость колонны относительно материальной оси, для чего определяем

и по λx определяем

где с = 1 – коэффициент условий работы по [1,табл.6].

Предельная гибкость колонны

где

–

коэффициент, учитывающий недонапряжение колонны.

Условие выполняется.

Расчет колонны на устойчивость относительно свободной оси y-y

Коэффициент μy = 2 (принята расчетная схема «консоль»)

Приведенная гибкость ef определяется по [1,табл.7] для колонны с планками

при

Приравнивая находим требуемое значение гибкости относительно свободной оси

Задаюсь

По λy находим радиус инерции

Воспользовавшись приближенными значениями радиусов инерции по [6,табл.11], определяем ширину сечения

Принимаем b = 900 мм.

Расстояние в свету между полками двутавров

Расстояние между ветвями увеличивать не требуется.

Проверка колонны на устойчивость относительно оси у-у.

Расчетная длина ветви

Принимаем расстояние в свету между планками lob = 126 см.

Длина планки bпл принимается равной расстоянию в свету между ветвями плюс напуск на ветви по 30 мм

Высоту планок hпл устанавливают в пределах (0,5…0,8)b=450…720 мм, где b = 900 мм – ширина сечения. Принимаем hпл = 540 мм.

Толщина планок принимается по условиям местной устойчивости и должна быть

Окончательно принимаем планку из листа 76054020 мм.

Все найденные размеры отражены на рис.16.

Рис. 16. Составной стержень колонны на планках

Момент инерции стержня относительно оси у-у

Радиус инерции

Гибкость

где

Приведенная гибкость

По [1,табл.72] в зависимости от ef находим коэффициент продольного изгиба  = 0,848.

Производим проверку

Устойчивость обеспечена.

Недонапряжение составило

6.3 Расчет планок

Расчет соединительных планок сжатых составных стержней выполняется на условную поперечную силу Qfic, принимаемую постоянной по всей длине стержня колонны и определяемую по формуле

где  = 0,848 – коэффициент продольного изгиба, принимаемый для составного стержня в плоскости соединительных элементов.

Поперечная сила, приходящаяся на планку одной грани

Сдвигающая сила в месте прикрепления планки к ветви колонны

Момент, изгибающий планку в ее плоскости,

Приварку планок толщиной tпл = 20 мм к полкам швеллеров производим полуавтоматической сваркой, принимая катет сварного шва kf = 6 мм.

Учитывая, что несущая способность планки больше, чем несущая способность сварного шва с катетом kf ≤ tпл, достаточно проверить прочность сварного шва. Расчет производится на равнодействующую напряжений в шве от изгибающего момента M1 и поперечной силы F.

Так как для полуавтоматической сварки

прочность шва проверяем по металлу шва.

– расчетная длина шва

– момент сопротивления расчетного сечения шва

Напряжение от изгиба

Напряжение от поперечной силы

где.

Проверяем прочность шва

Прочность обеспечена.

6.4 Конструирование и расчет оголовка сквозной колонны

Оголовок состоит из плиты и диафрагмы, подкрепленной горизонтальным ребром жесткости (рис.17).

Толщина диафрагмы td определяется расчетом на смятие от продольной силы N

где – условная длина распределения нагрузки, равная ширине опорного ребра главной балки bh плюс две толщины оголовка колонны (ton принята 25 мм), за минусом толщины диафрагмы (≈2tw) и 40 мм для пропуска швов.

Принимаем td = 36 мм.

Рис. 17. Оголовок сквозной колонны

Высота диафрагмы определяется из условия среза стенок ветвей колонны (tw = 8,8 мм – толщина стенки для принятого двутавра 50Б1).

Принимаем hd = 80 см.

Проверяем диафрагму на срез как короткую балку

где Q = N/2 = 3748/2 = 1874 кН.

Условие прочности выполняется.

Определяем катет сварного шва, обеспечивающего прикрепление диафрагмы к стенке ветвей колонны (расчет по металлу шва)

где – расчетная длина шва, равная высоте диафрагмы за вычетом 1 см, учитывающего дефекты в концевых участках шва.

Принимаем катет шва kf = 8 мм, что отвечает минимальной его величине при полуавтоматической сварке элементов t = 36 мм.

Расчетная длина флангового шва должна быть не более 85βfkf. Проверяем lw = 79 < 850,90,8 = 61,2 см, что не удовлетворяет условию.

Принимаем катет шва kf = 11 мм, проверяем lw = 79 < 850,91,1 = 84,15 см, что удовлетворяет условию.

Толщину горизонтального ребра жесткости

Принимаю ts = 12 мм.

Ширину bs назначаем из условия устойчивости ребра

Принимаем bs = 36 см.

6.5 Конструирование и расчет базы колонны

6.5.1 Определение размеров опорной плиты в плане

Определяем расчетное усилие в колонне на уровне базы с учетом собственного веса колонны

где k = 1,2 – конструктивный коэффициент, учитывающий вес решетки, элементов базы и оголовка колонны. Давление под плитой принимается равномерно распределенным. В центрально-сжатой колонке размеры плиты в плане определяются из условия прочности фундамента

где  – коэффициент, зависящий от характера распределения местной нагрузки по площади смятия (при равномерно распределенной нагрузке  =1);

Rb,loc – расчетное сопротивление бетона смятию, определяемое по формуле

где  = 1 – для бетона класса ниже B25;

Rb = 7,5 МПа для класса бетона B12,5 – расчетное сопротивление бетона сжатию;

b – коэффициент, учитывающий повышение прочности бетона сжатию в стесненных условиях под опорной плитой и определяемый по формуле

Предварительно задаемся b = 1,2.

Принимаю две отдельные плиты (связываются между собой швеллером) под каждую ветвь колонны.

Размеры каждой плиты (ширина B и длина L) назначаются по требуемой площади A’p =Ap/2 = 4167/2 = 2083 см2, увязываются с контуром колонны и согласуются с сортаментом.

Назначаем длину одной плиты

где h = 49,2 см – высота сечения стержня колонны (двутавр 50Б1);

tt = 10 мм – толщина траверсы, принимаемая (8…16 мм);

с = 50 мм – вылет консольной части плиты, принимается предварительно и уточняется в процессе расчета толщины плиты.

Требуемая ширина одной плиты

Принимаем В = 340 мм, L = 630 мм. Площадь одной плиты A’p=2142 см2>2083 см2. Площадь двух плит Ap=4284 см2. Размеры верхнего обреза фундамента устанавливаем на 20 см больше размеров опорной плиты.

Площадь

Коэффициент

6.5.2 Определение толщины опорной плиты

Толщина опорной плиты определяется из условия ее прочности на изгиб как пластинки, опертой на торец колонны, траверс и ребер, от отпора фундамента, равного среднему напряжению под плитой

Для расчета плиты выделяются участки пластинки, опертые по четырем, трем и одной (консольные) сторонам, соответственно обозначенные цифрами 1, 2, 3 (рис.18).

В каждом участке определяются максимальные изгибающие моменты, действующие на полосе шириной 1см, от расчетной равномерно распределенной нагрузки

Рис.18. К расчету опорной плиты

На участке 1, опертом по четырем сторонам

где 1 =– коэффициент, учитывающий уменьшение пролетного момента за счет опирания плиты по четырем сторонам, определяется в зависимости от отношение большей стороны участки b к меньшей a по [6, табл.13].

Значения b и a определяются по рис.18:

b = H – 2tf = 49,2 – 21,2=46,8 см; а = bb/2 – tw/2 = 20/2 – 0,88/2 = 9,56 см; b/а = 46,8/9,56 = 4,895.

При b/a > 2 при опирании плиты на четыре канта изгибающий момент определяется как для однопролетной балочной плиты пролетом а

На участке 2, опертом по трем сторонам

где  – коэффициент, принимаемый в зависимости от отношения закрепленной стороны пластинки b1 к свободной а1 по [6, табл.14].

Отношение сторон b1/a1 = 69/200 = 0,345; при отношении сторон b1/a1 < 0,5 плита рассчитывается как консоль длиной b1 (рис.36)

На консольном участке 3

По наибольшему из найденных для участков плиты изгибающих моментов (участок 2) определяем требуемый момент сопротивления плиты шириной 1 см

откуда

Принимаем лист толщиной 25 мм.

6.5.3 Высота траверсы

Высота траверсы определяется из условия размещения вертикальных швов крепления траверсы к стержню колонны. Катетом шва задаемся в пределах 8…16 мм, но не более 1,2tmin.

Рис. 19. К расчету траверсы и ребра усиления плиты

Принимаем kf = 9 мм. Требуемая длина одного шва, выполненного полуавтоматической сваркой,

Принимаем высоту траверсы с учетом добавления 1 см на дефекты в начале и конце шва ht = 34 см. Проверяется прочность траверсы как однопролетной двухконсольной балки, опирающейся на ветви (полки) колонны и воспринимающей отпорное давление от фундамента (рис.19).

Равномерно распределенная нагрузка на траверсу

где d = B/2 = 34/2 = 17 см – ширина грузовой площади траверсы.

Определяем усилия:

– на опоре

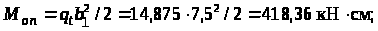
– в пролете

Момент сопротивления траверсы

Проверяем прочность траверсы:

– по нормальным напряжениям от максимального момента

– по касательным напряжениям

– по приведенным напряжениям

Условие не выполняется.

Принимаем высоту траверсы ht = 36 см

Момент сопротивления траверсы

Проверяем прочность траверсы:

– по нормальным напряжениям от максимального момента

– по касательным напряжениям

– по приведенным напряжениям

Условие выполняется.

Требуемый катет горизонтальных швов для передачи усилия (Nt = qtL) от одной траверсы на плиту

где lw = (L–1)+2(b1–1) = (63–1)+2(6,9–1)=73,8 см – суммарная длина горизонтальных швов.

Принимаем kf = 8 мм.

Список литературы

СНиП II-23-81*.Стальные конструкции. Нормы проектирования. /Госстрой России. – М.: ГУП ЦПП, 1998.– 96с.
СНиП 2.01.07-85*. Нагрузки и воздействия. Госстрой России. –М.: ГП ЦПП, 2003.– 44с.
Металлические конструкции. В 3т. Т.1. Элементы конструкций: Учеб. для строит. вузов /В.В. Горев, Б.Ю. Уваров, В.В. Филиппов и др.; Под ред. В.В. Горева.–2-е изд., перераб. и доп. – М.: Высш. шк., 2001.– 551с.: ил.
Металлические конструкции. Общий курс: Учеб. для вузов /Г.С. Ведеников, Е.И. Беленя, В.С. Игнатьева и др.; Под ред. Г.С. Веденикова. –7-е изд., перераб. и доп. – М.: Стройиздат, 1998.– 760с.: ил.
Металлические конструкции. В 3т. Т. Общая часть. (Справочник проектировщика) /Под общ. ред. В.В.Кузнецова. – М.: Изд. – во АСВ, 1998. – 576 с.: ил.
Металлические конструкции. Пособие по проектированию рабочей площадки производственного здания. Составил В.Г. Темников – Иркутск: Изд. ИрГТУ, 2003. 76 с.