Компоновка сборного перекрытия

Содержание

1. Компоновка сборного железобетонного перекрытия

2. Проектирование предварительно напряжённой плиты

2.1 Сбор нагрузок на перекрытие

2.2 Данные для расчёта

2.3 Нагрузки

2.5 Компоновка поперечного сечения панели

2.6 Расчёт полки на местный изгиб

2.7 Расчёт прочности сечений нормальных к продольной оси

2.8 Расчёт прочности по наклонным сечениям

2.9 Расчёт преднапряжённой плиты по предельным состояниям II группы

2.10 Расчёт по образованию трещин нормальных к продольной оси

2.11 Расчёт прогиба плиты

2.12 Расчёт плиты при монтаже

3. Проектирование наразрезного ригеля

3.1 Определение нагрузок

3.1.1 Вычисление изгибающих моментов в расчётной схеме

3.1.2 Перераспределение моментов под влиянием образования пластических шарниров

3.2 Расчёт прочности ригеля по сечениям нормальным к продольной оси

3.3 Расчёт прочности ригеля по сечениям наклонным к продольной оси

3.4 Построение эпюры материалов ригеля в крайнем и среднем пролёте

4. Расчёт прочности колонны

4.1 Сбор нагрузок на колонны

4.2 Определение расчётной продольной нагрузки на колонну

4.3 Определение изгибающих моментов колонны от расчётной нагрузки

4.4 Расчёт прочности колонны первого этажа

4.5 Расчёт консоли колонны

4.6 Расчёт стыка колонны

4.7 Расчёт стыка ригеля с колонной

5. Расчёт и конструирование отдельного железобетонного фундамента

6. Расчёт и конструирование монолитного перекрытия

6.1 Компоновка ребристого монолитного перекрытия

6.2 Расчёт многопролётной плиты монолитного перекрытия

6.2.1 Расчётный пролёт и нагрузки

6.3 Расчёт многопролётной второстепенной балки

6.3.1 Расчётный пролёт и нагрузки

6.3.2 Расчётные усилия

6.3.3 Определение высоты балки

6.3.4 Расчёт прочности по сечениям нормальным к продольной оси

6.3.5 Расчёт прочности второстепенной балки по сечениям наклонным к продольной оси

1. Компоновка конструктивной схемы сборного перекрытия

Ригели поперечных рам – трёхпролётные, на опорах жёстко соединены со средними колоннами, на стены опёрты шарнирно. Плиты перекрытий предварительно напряжённые многопустотные номинальной шириной 1900 мм и 2100 мм; связевые плиты номинальной шириной 2100 мм размещают по рядам колонн.

Рисунок 1 – Компоновка конструктивной схемы сборного перекрытия

2. Расчёт многопустотной плиты по предельным состояниям первой группы

Исходные данные. Многопустотная плита из тяжелого бетона класса В40 опирается поверху на железобетонные ригели каркаса, пролет ригелей – l_>p>=5,9 м. Нормативное значение временной нагрузки 3,5 кПа. Требуется рассчитать и законструировать плиту перекрытия. Класс рабочей арматуры принять А-V.

2.1 Расчет плиты по предельным состояниям первой группы

2.1.1 Расчётный пролёт и нагрузки

Для установления расчётного пролёта плиты предварительно задаёмся размерами сечения ригеля:

h_>p>=(1/12)*l_>p>=(1/12)*590=50 см, b_>p>=0.5*h_>p>=0.4*50=20 см.

При опирании на ригель поверху расчётный пролёт плиты составит:

l_>o>=l-b_>p>/2=6,4–0,2/2=6,3 м.

Подсчёт нагрузок на 1м² перекрытия сводим в таблицу 1.

Таблица 1 – Нормативные и расчётные нагрузки на 1 м² перекрытия

Нагрузка	Нормативная нагрузка, Н/м²	Коэффициент надёжности по нагрузке	Расчётная нагрузка, Н/м²
Постоянная Собственный вес многопустотной плиты с круглыми пустотами	3000	1,1	3300
То же слоя цементного раствора =20 мм (=2200 кг/м³)	440	1,3	570
То же керамических плиток =13 мм (=1800 кг/м³)	240	1,1	264
Итого	3680	-	4134
Временная	3500	1,2	4200
В том числе длительная	2450	1,2	2940
Кратковременная (30%)	1050	1,2	1260
Полная нагрузка	7180	-	8334
В том числе: Постоянная и длительная	6130	-	7074

На 1 м длины плиты шириной плиты 2,1 м действуют следующие нагрузки, Н/м: кратковременная нормативная pⁿ=1050*2,1=2205; кратковременная расчетная р=1260*2,1=2646; постоянная и длительная нормативная qⁿ=6130*2,1=12873; постоянная и длительная расчетная q=7074*2,1=14855,4; итого нормативная qⁿ+pⁿ=12873+2205=15078; итого расчетная q+p=14855,4+2646=17501,4.

2.1.2 Усилия от расчётных и нормативных нагрузок

Расчётный изгибающий момент от полной нагрузки:

M=(q+p)*l²_>0>*_>n>/8=17501,4*6,3²*0.95/8=82487,4Н^.м.

Расчетный изгибающий момент от полной нормативной нагрузки:

Mⁿ=(qⁿ+pⁿ)*l²_>0>*_>n>/8=15078*6,3²*0.95/8=71065,4Н^.м.

То же, от нормативной постоянной и длительной временной нагрузок:

M_>ld>=qⁿ*l²_>0>*_>n>/8=12873*6,3²*0.95/8=60672,9Н^.м.

То же, от нормативной кратковременной нагрузки:

M_>с>_>d>=рⁿ*l²_>0>*_>n>/8=2205*6,3²*0.95/8=10392,6Н^.м.

Максимальная поперечная сила на опоре от расчетной нагрузки:

Q=(q+p)*l_>0>*_>n>/2=17501,4*6,3*0.95/2=52372,9Н.

То же, от нормативной нагрузки:

Qⁿ=(qⁿ+pⁿ)*l_>0>*_>n>/2=15078*6,3*0.95/2=45120,9Н.

То же, от нормативной нагрузки:

Qⁿ_>ld>=qⁿ*l_>0>*_>n>/2=12873*6,3*0.95/2=38522,5Н.

2.1.3 Установление размеров сечения плиты

Плиту рассчитываем как балку прямоугольного сечения с заданными размерами bxh=210х22 см (где b – номинальная ширина, h – высота плиты). Проектируем плиту одиннадцатипустотной. В расчете поперечное сечение пустотной плиты приводим к эквивалентному двутавровому сечению. Заменяем площадь круглых пустот прямоугольниками той же площади и того же момента инерции.

Вычисляем:

h_>1>=0.9*d=0.9*15.9=14.3 см;

h_>f>=h_>f>’=(h-h_>1>)/2=(22–14.3)/2=3.8 см;

тогда приведенная толщина ребер равна:

b_>p>=b=b_>f>’ – n*h_>1>=207–11*14.3=49,7 см,

где b_>f>’=207 см – расчетная ширина сжатой полки.

Приведенная толщина бетона плиты:

h_>red>=h – (n**d²)/4b=22 – (11**15.9²)/(4*207)=11.5 см>10 см.

Рабочая высота сечения h_>0>=22–3=19 см.

Толщина верхней и нижней полок h_>f>=(22–15.9)^.0.5=3 см.

Ширина ребер: средних – 2.9 см, крайних – 3 см.

2.1.4 Характеристики прочности бетона и арматуры

Плита изготавливается из тяжелого бетона класса В40, имеет предварительно напрягаемую рабочую арматуру класса А-VI с электротермическим натяжением на упоры форм. К трещиностойкости плиты предъявляются требования 3 ей категории. Изделие подвергают тепловой обработке при атмосферном давлении.

Бетон тяжёлый класса В40

Призменная прочность бетона нормативная: R_>bn>=R_>b,ser>=29МПа, расчётная R_>b>=22МПа, коэффициент условий работы бетона _>b2>=0.9; нормативное сопротивление при растяжении R_>btn>=R_>bt,ser>=2.1МПа, расчётное R_>bt>=1.4МПа; начальный модуль упругости бетона E_>b>=32.5*10³МПа.

Передаточная прочность бетона R_>bp> устанавливается так, чтобы при обжатии отношение напряжений _>bp>/R_>bp>0.75.

Арматура продольная класса A-VI

Нормативное сопротивление R_>sn>=R_>s,ser>=980МПа,

Расчётное сопротивление R_>s>=225МПа,

Модуль упругости E_>s>=1.9*10⁵МПа.

Предварительное напряжение арматуры назначаем таким образом, чтобы выполнялись условия . При электротермическом способе натяжения:

Принимаем _>sp>=600МПа.

Определяем коэффициент точности натяжения арматуры

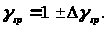
где n – число стержней напрягаемой арматуры, принимаем n=8.

При благоприятных влияниях предварительного напряжения _>sp>=1–0.1= 0,9. При проверке по образованию начальных трещин в верхней зоне плиты '_>sp> =1+0.1=1.1. Значение предварительного напряжения с учётом точности натяжения арматуры составит 0.9*600=540МПа.

2.1.4 Расчёт прочности плиты по сечению, нормальному к продольной оси

При расчёте прочности, сечение плиты принимается тавровым (полка нижней растянутой зоны в расчёт не вводится). Размеры сечения показаны на рисунке 2б. Вычисляем:

Находим

Высота сжатой зоны сечения: следовательно, нейтральная ось проходит в пределах сжатой полки, и сечение рассчитывается как прямоугольное шириной b_>f>^’=207 см.

Вычисляем характеристики сжатой зоны

ω=0,85–0,008·R_>b>=0,85–0,008·22·0,9=0,69

Вычисляем граничную высоту сжатой зоны

ξ_>R>=

где σ_>SR>=R_>s>+400 – σ_>SP>_>2>

σ_>SP>=0,6R_>sn>=0,6·785=471 МПа

σ_>SP2>=γ_>sp>· σ_>SP>·0,7=0,84·471·0,7=276,95 МПа

σ_>SR>=680+400–276,95=803,1 МПа.

Поскольку соблюдается условие <_>R> (0.034<0.43), то расчётное сопротивление арматуры умножается на коэффициент условий работы _>s>_>6>:

где =1.15 – коэффициент, принимаемый равным для арматуры класса A-V.

Требуемую площадь сечения рабочей арматуры определяем по формуле:

где =1–0.5=1–0.5*0.058=0.971.

Принимаем в качестве предварительно напряжённой продольной рабочей арматуры три стержня арматуры класса A-V 316 мм с общей площадью A_>sp>=6,03см². Арматура устанавливается в четвертом слева и крайних рёбрах плиты.

2.3.5 Расчёт прочности плиты по наклонным сечениям

По конструктивным требованиям в многопустотных плитах высотой не более 30 см поперечная арматура не устанавливается, если она не нужна по расчету. Проверим необходимость постановки поперечной арматуры расчетом. Проверяем условие:

Q 0.3_>w1>_>b1>R_>b> b h_>0>,

где Q – поперечная сила на опоре от расчетной нагрузки; Q=52,37кН,

_>w1>=1, так как поперечная арматура отсутствует;

_>b1>=1–0.01R_>b>=1–0.01*22=0.78.

Условие:

52,37<0.3*1*0.78*22*10^-1*49,7*19,

52,37кН<486,13кН, выполняется,

следовательно, прочность плиты по наклонной полосе между наклонными трещинами обеспечена.

Поперечную арматуру в плите можно не устанавливать, если выполняются условия:

а) Q_>max>2.5*R_>bt>*b*h_>0>; Q_>max>=Q.

52,37<2.5*1.4*10^-1*49,7*19,

52,37кН<330,51кН, условие выполняется.

б) Q_>1>M_>b>_>1>/c, Q_>1>=Q_>max>-q_>1>*c=52,37–11,88*0.475=46,73кН,

где с – проекция наклонного сечения, принимаем:

с=2,5h_>0>=2,5*19=47,5 см;

q=g^p*b*_>f>=8,334*1,5*0,95=11,88кН/м,

М_>b1>=_>b4>(1+_>n>)_>b2>R_>bt>*b*h_>0>²;

_>b>_>4>=1.5 – для тяжелого бетона; _>n>=0;

где Р=A_>sp>(_>sp>-100)=5,96*(540–100)*0.1 = 262 кН – усилие предварительного обжатия,

100 МПа – минимальное значение суммарных потерь предварительного напряжения.

Принимаем _>n>=0.5.

М_>b>_>1>=1,5*(1+0,22)*0,9*1,4*10^-1*49,7*19²= 4137 кН*см.

М_>b>_>1>/с=4137/47,5 = 87,09 кН.

Условие Q_>1>М_>b>_>1>/с: 46,73 кН<87,09 кН выполняется, следовательно, поперечную арматуру в плите не устанавливаем.

На приопорных участках длиной l/4 арматуру устанавливаем конструктивно 4 Вр-I с шагом S=h/2=22/2=11 см, в средней части пролёта поперечную арматуру не устанавливаем.

3.2 Расчет плиты по предельным состояниям второй группы

3.2.1 Геометрические характеристики сечения

При расчёте по 2-ой группе предельных состояний в расчёт водится двутавровое сечение плиты (рисунок 2в).

Площадь приведённого сечения:

расстояние от нижней грани до центра тяжести приведённого сечения:

момент инерции сечения:

момент сопротивления сечения:

упругопластический момент сопротивления по растянутой зоне

здесь =1.5 для двутаврового сечения при 2<b_>f>/b=207/49,7=4,2<6,0.

Упругопластический момент по растянутой зоне в стадии изготовления и обжатия W_>pl>’=W_>pl>=20343см³.

Расстояния от ядровых точек – наиболее и наименее удалённой от растянутой зоны (верхней и нижней) – до центра тяжести сечения:

3.2.2 Потери предварительного напряжения

Расчёт потерь выполняем в соответствии с требованиями СНиП 2.03.01–84*. Коэффициент точности натяжения арматуры принимаем _>sp>=1.0.

Потери _>1> от релаксации напряжений при электротермическом натяжении высокопрочных канатов: _>1>=0.03*_>sp>=0.03*600 = 18 МПа.

Потери _>2> от температурного перепада между натянутой арматурой и упорами равны нулю, так как при пропаривании форма с упорами нагревается вместе с изделием.

Потери от деформации анкеров _>3> и формы _>5> при электротермическом способе равны нулю. Поскольку арматура не отгибается, потери от трения арматуры _>4> также равны нулю.

Усилие обжатия

Эксцентриситет силы Р_>1> относительно центра тяжести сечения е_>ор>=у_>0>-а=11–3 = 8 см.

Определим сжимающие напряжения в бетоне:

где Mg=q*l²/8=(2,07*3,0)*6,4²/8 = 31,8 кНм – изгибающий момент в середине пролета плиты от собственного веса,

l=6,4 м – расстояние между прокладками при хранении плиты.

Устанавливаем значение передаточной прочности бетона из условия _>bp>/R_>bp>0.75, но не менее 0.5В (В-класс бетона):

0,78 МПа,

0,5 B=0,5*40 = 20 МПа.

Принимаем R_>bp>=20МПа, тогда:

при расчёте потерь от быстронатекающей ползучести _>6> при

Итак, первые потери _>los>_>1>=_>1>+_>6>=18+0,79=18,79МПа.

С учётом потерь _>los1>:

Р_>1>=А_>sp>(_>sp>-_>los1>)=5,96*(600–18,79)*10^-1=346,4МПа.

Отношение .

Из вторых потерь _>7>…_>11> при принятом способе натяжения арматуры учитываются только потери _>8> от усадки бетона и потери _>9> от ползучести бетона.

Для тяжёлого бетона классов В40 и ниже _>8>= 40 МПа.

Так как _>bp>/R_>bp><0.75 то _>9>=127.9*_>bp>/R_>bp>=112,5*0,029 = 3,26 МПа.

Вторые потери _>los>_>2>=_>8>+_>9>=40+3,26 = 43,26 МПа.

Полные потери _>los>=_>los>_>1>+_>los>_>2>=18,79+43,26=62,05МПа<100МПа, принимаем _>los>= 100 МПа.

Усилие обжатия с учётом полных потерь:

Р_>2>=А_>sp>(_>sp>-_>los>)=5,96*(600–100)*10^-1=298кН.

4.2.3 Расчёт по образованию нормальных трещин

Образование нормальных трещин в нижней растянутой зоне плиты не происходит, если соблюдается условие M_>n>=71,065кН*мM_>crc>_>>(M_>crc> – момент образования трещин):

Поскольку M_>n><M_>crc> (71,065<79,52), то в нижней зоне плиты трещины не образуются.

Проверим, образуются ли начальные трещины в верхней зоне плиты от усилия предварительного обжатия.

Расчётное условие:

здесь R_>bt>_>,>_>p>= 1 МПа – нормативное сопротивление бетона растяжению, соответствующее передаточной прочности бетона R_>bp>=20 МПа;

Р_>1> – принимается с учётом потерь только _>1>, Р_>1>= 346,4 кН;

M_>g> – изгибающий момент в середине пролёта плиты от собственного веса, M_>g>=31,8 кН*м.

Вычисляем: 1.12*346,4*(8–5,72)1*10^-1*20343,5+31,8,

884,57 кН*см<2066,2 кН*см.

Условие выполняется, значит, начальные трещины в верхней зоне плиты от усилия предварительного обжатия не образуются.

4.2.4 Расчёт прогиба плиты

Для однопролётной шарнирно опертой балочной плиты прогиб можно определить по формуле:

где 1/r – кривизна оси элемента при изгибе.

Кривизна оси элемента, где не образуются трещины при длительном действии нагрузки:

где _>b>_>1>= 0.85 – коэффициент, учитывающий снижение жесткости под влиянием неупругих деформаций бетона растянутой зоны;

_>b>_>2> – коэффициент, учитывающий снижение жёсткости (увеличение кривизны) при длительном действии нагрузки под влиянием ползучести бетона сжатой зоны при средней относительной влажности воздуха выше 40%, равна 2;

_>b2> – то же, при кратковременной нагрузке равна 1.

Так как в растянутой зоне плиты трещины не образуются, то кривизна оси (без учета влияния выгиба):

где – кривизна соответственно от кратковременных и от постоянных и длительных нагрузок,

Тогда прогиб будет равен:

От постоянной и длительной временной нагрузок:

Тогда прогиб будет равен:

Тогда полный прогиб будет равен:

4.3 Проверка панели на монтажные нагрузки

Панель имеет четыре монтажные петли из стали класса А-1, расположенные на расстоянии 70 см от концов панели (рисунок 3а). С учётом коэффициента динамичности _>d>=1.4 расчётная нагрузка от собственного веса панели:

где собственный вес панели; b_>п> – конструктивная ширина панели; h_>red> – приведённая толщина панели;  – плотность бетона.

Расчётная схема панели показана на рисунке 3б. Отрицательный изгибающий момент консольной части панели:

Этот момент воспринимается продольной монтажной арматурой каркасов. Полагая, что z_>1>=0.9*h_>0>=0.9*19=17.1 см, требуемая площадь сечения указанной арматуры составляет:

что значительно меньше принятой конструктивно арматуры 316 А-II, А_>s>=5,96 см².

При подъёме панели вес её может быть передан на две петли. Тогда усилие на одну петлю составляет

Площадь сечения арматуры петли

принимаем конструктивно стержни диаметром 14 мм, А_>s>=1,539 см².

3. Проектирование неразрезного ригеля

3.1 Определение нагрузок

Предварительно задаёмся размерами сечения ригеля

Длина ригеля в середине пролёта

Длина крайнего ригеля

Из таблице 1, постоянная нагрузка на 1м²ригеля равна:

– нормативная Па

– расчётная Па

временная нагрузка

– нормативная 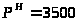Па

– расчётная Па

Нагрузка от собственного веса ригеля:

с учётам коэффициента

с учётом коэффициента

Итого

Временная с учётом коэффициента

Полная расчётная нагрузка

3.1.1 Вычисление изгибающих моментов в расчётной схеме

1) Вычисляем опорные моменты и заносим в таблицу

2) Вычисляем опорные моменты при различных схемах загружения и заносим в таблицу.

Таблица 2 – Ведомость усилий в ригеле

№ п/п	Схема загружения	Опорные моменты
М_>21>	М_>23>	М_>32>
1
2
3
4
№ нагр	Опорные моменты	Пролётные моменты	Поперечные силы
М_>21>	М_>23>	М_>32>	М_>1>	М_>2>	Q_>1>	Q_>21>	Q_>23>
1+2	208,46	109,02	109,02	159,34	12,64	130,61	198,41	82,48
1+3	142,78	149,03	149,03	217,11	83,76	61,75	110,21	157,83
1+4	235,51	181,92	138,36	148,94	50,87	126,22	202,8	157,83
(1+4)	164,85	164,85	132,67	176,96	69,82	137,71	191,31	152,38

Вычисляем пролётные моменты и поперечные силы

1) кН.

кН м.

кНм.

кН

кНм.

2) кН.

кН м.

кНм.

кН

кНм.

3) кН.

кН м.

кНм.

кН

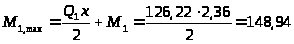кНм.

3.1.2 Перераспределение моментов под влиянием образования пластических шарниров

Наибольший опорный момент уменьшаем на 30% по схеме загружения 1+4

кНм

кНм.

кНм

Находим поперечные силы

кН.

кН м.

кНм.

кНм.кНм.

кН

кН. м.

кНм.

Р
исунок 3 – Эпюры моментов

а) – эпюры по схеме загружения

б) – выравнивающая эпюра

в) – перераспределённая эпюра

3.2 Расчёт прочности ригеля по сечениям нормальным к продольной оси

Высоту сечения ригеля подбираем по опорному моменту М=164,85 кНм при ξ=0,35.

По заданию марка бетона В40, арматура АV. Определяем граничную высоту сжатой зоны.

ξ_>R>=

где =0,85–0,008·22·0,9=0,69

МПа

МПа (<1)

Высота сечения ригеля при ширине сечения 200 мм

Так как b принимается в пределах , то для согласования этих размеров принимаем b=150 мм, тогда

см

Полная высота сечения

см

Подбираем сечение арматуры в различных сечениях ригеля

Сечение в первом пролёте

М=176,96 кНм

α_>m>=

Из таблицы находим η=0,81

А_>s>= см²

Принимаем 4Ø16 АV см²

Сечение во втором пролёте

М = 83,76 кНм

α_>m>=

Из таблицы находим η=0,92

А_>s>= см²

Принимаем 4Ø10 АV см²

Сечение на первой опоре со стороны первого пролёта

М = 235,51 кНм

α_>m>=

Из таблицы находим η=0,715

А_>s>= см²

Принимаем 4Ø20 АV см²

Сечение на первой опоре со стороны второго пролёта

М = 149,03 кНм

α_>m>=

Из таблицы находим η=0,846

А_>s>= см²

Принимаем 4Ø14 АV см²

3.3 Расчёт прочности ригеля по сечениям наклонным к продольной оси

Диаметр поперечных стержней определяют из условия сварки их с продольной арматурой d=20 мм и принимают равным d_>sw>=6 мм. На приопорных участка устанавливаем поперечную арматуру с шагом S=15 см, в середине пролёта S==35 cм.

Принимаем 2 каркаса d_>sw>=6 мм см² арматура класса АIII

МПа

Н/см

Проверяем условие обеспечения прочности сечения

<1075,4→ условие прочности удовлетворяется

Требование см>15 см→ требование удовлетворяется.

Рассчитываем прочность по наклонному сечению:

Для этого вычисляем кНм так каккН/cм<0,56g_>sw>=0,56·1075,4 = 602,22 кН/cм

см<3,33·h_>0>=3,33·44 = 146,52 см

При этом кН>49,9 кН

Поперечная сила в вершине наклонного сечения

137,71·10³-407,3·134,04 = 83,12 кН

Длина проекции наклонного сечения

Условие прочности >83,12→прочность обеспечивается.

3.4 Построение эпюры материалов ригеля в крайнем и среднем пролёте

Рассмотрим сечение первого пролёта

4Ø16 АV см² h_>0>=44cм

кНм

Арматуру 2 Ø16 доводим до опор 2Ø16 обрывается

Определяем момент воспринимаемый сечением арматуры 2Ø16 АV см²

кНм

Сечение во втором пролёте

4Ø10 АV см²

кНм

Арматуру 2 Ø10 доводим до опор и 2Ø10 обрывается

Определяем момент воспринимаемый сечением арматуры 2Ø10 АV

см²

кНм

Сечение на первой опоре со стороны первого пролёта

4Ø20 АV см²

кНм

Арматура 2 Ø20 доводим до опор и 2Ø20 обрывается

Определяем момент воспринимаемый сечением арматуры 2Ø20 АV см²

кНм

Сечение на первой опоре со стороны второго пролёта

4Ø14 АV см²

кНм

Арматура 2 Ø14 доводим до опор и 2Ø14 обрывается

Определяем момент воспринимаемый сечением арматуры 2Ø14 АV см²

кНм

Определяем места теоретического обрыва продольных рабочих стержней и длину их анкеровки.

1029,6 кН/м

Поперечные силы в местах теоретического обрыва стержней определяем по эпюре Q

1) Q_>1>=76,15 кН; d=18

см<20·d=20·1,8=36

2) Q_>2>=89,43 кН; d=18

см<20·d=20·1,8=36

3) Q_>3>=160,78 кН; d=1,8

см<20·d=20·1,8=36

4) Q_>4>=135,63 кН; d=12

см<20·d=20·1,2=24

5) Q_>5>=76,53 кН; d=16

см<20·d=20·1,6 = 32

6) Q_>6>=76,53 кН; d=16

см < 20·d=20·1,6 = 32

Р
ис. 4 Эпюра материалов ригеля

4. Расчёт прочности колонны

4.1 Сбор нагрузок на колонны

Сетка колонн 5,9х6,4 м, высота первого этажа 4,2 м, высота последующих 4,2 м, количество этажей 3. Нормативная нагрузка 3,5 кПа, район строительства – г Кострома. IV – снеговой район.

Бетон В 25 МПа, , арматура АII Мпа

Таблица – Сбор нагрузок на 1 м² на колонну

№ п/п	Наименование нагрузок	Нормативная Нагрузка кН	Коэффициент надёжности	Расчётная нагрузка
1	Покрытие а) вес кровли б) вес ж/б плиты в) вес ригеля	2,11 2,8 0,31	1,1 1,1 1,1	2,32 3,08 0,34
	Итого нагрузка	5,22		5,74
2	Временная от снегового района	1,5	1,4	2,1
3	Перекрытие Вес констр. пола и плиты перекрытия вес ригеля	3,65 0,31	1,1 1,1	4,02 0,34
	Итого постоянная	3,96		4,36
4	Временная на перекрытие длительная кратковременная	3,5 2,45 1,05	1,2 1,2 1,2	4,2 2,94 1,26
	постдлительная нагр. на перекрытие	6,41		7,3

4.2 Определение расчётной продольной нагрузки на колонну

Грузовая площадь равна м²

Собственный вес колонны сечением 30х30 и длиной 4,2 м с коэффициентом надёжности

=10,4

От покрытия

– длительная кН

– кратковременная кН

От перекрытия

– длительная кН

– кратковременная кН

3-й этаж

кН

2-й этаж

кН

1-й этаж

кН

4.3 Определение изгибающих моментов колонны от расчётной нагрузки

Находим при вычисленных размерах ригеля 50х15 см и сечении колонны 30х30.

Отношение погонных жесткостей, вводимых в расчёт.

Определяем максимальные моменты колонны при загружении 1+4 без перераспределения моментов. g=27,96, временная , длительная , кратковременная

При длительной нагрузке кНм; кНм.

При полной нагрузке кНм.

кНм

Разность абсолютных значений опорных моментов в узле рамы от длительных нагрузок кНм, от полной нагрузки кНм.

Изгибающие момента колонны подвала от длительных нагрузок кНм, от полной

кНм

Изгибающие момента колонны 1-го этажа от длительных нагрузок кНм, от полной

кНм

4.4 Расчёт прочности колонны первого этажа

кН; кНм, кНм

Задаёмся =1, =0,025. Предварительно определяем сечение колонны

см²

Сечение колонны принимаем 30х40 с площадью поперечного сечения 900 см²

Рабочая высота сечения см

Эксцентриситет силы

см, случайный эксцентриситет

см.

см. Для расчёта принимаем е=7,07 см.

Момент относительно растянутой арматуры

при длительной нагрузке кНм
_{>при полной нагрузке}> кНм

Определяем гибкость колонны при радиусе инерции

14 см

Для вычисления критической силы находим

- для тяжёлого бетона

_>min> принимаем =0,24

; =0,025

Вычисляем критическую силу по формуле

Вычисляем коэффициент 

см

Определяем граничную высоту сжатой зоны



где



Определяем площадь армирования

Принимаем 4Ø25 А_>s>=19,63 см²

Коэффициент армирования для расчёта брали μ=0,025

→ решение можно считать найденным.

Поперечную арматуру принимаем d=8 мм.

4.5 Расчёт консоли колонны

Р
азмеры площадки консоли колонны определяются от опорного давления ригеля и составляет Q=202,8 кН.

Рис. 5 К расчёту консоли колонны

Принимаем l=20 см, при b_>р>=15 см.

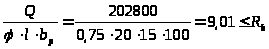=14,5

Вылет консоли с учётом зазора принимаем l_>1>=25 см

Высоту сечения консоли у грани колонны принимают равной , при угле наклона сжатой грани =45 высота консоли у свободного края . Рабочая высота сечения консоли . Поскольку консоль короткая.

Рассчитываем армирование консоли. Консоль армируется продольной и поперечной арматурой. Изгибающий момент у грани колонны кНм. Расчётный изгибающий момент принимаем на 25% больше кНм.

Для определения площади продольной арматуры находим

α_>m>=

Из таблицы находим η=0,963

А_>s>= см²

Принимаем 216 А с см²

Консоль армируют горизонтальными хомутами 6 А с см², с шагом S=10 см (при этом см и ) и отгибами 216  _>>=4,02 см².

Проверяем прочность сечения консоли по условию

;

прочность обеспечена.

4.6 Расчёт стыка колонны

Рассчитываем стык колонны между первым и вторым этажом. Колонны стыкуют сваркой стальных листов между которыми устанавливаются при монтаже центрирующая прокладка толщиной 5 мм. Расчётное усилие в стыке принимаем по усилиям второго этажа N=642,73 кН. Концы колонны усиливают сварными сетками косвенного армирования, т. к. продольная арматура колонн в зоне стыка обрывается. Сварные сетки из арматуры класса А d_>s>=6 мм. Количество сеток не менее 4-х штук.

Находим коэффициент косвенного армирования

где - соответственно количество стержней, площадь сечения и длина стержня вдоль осей х и у (т.е. в продольном и поперечном направлении)

Назначаем размеры ячеек сетки колонны. При размерах сечения шаг сеток должен удовлетворять соотношению . При шаг (мм.) принимаем равным s=55 мм. Число стержней , длина стержня (считая выступы по 10 мм) равна при этом см². площадь сечения одного стержня d=6 мм см², при шаге s=10 см=100 мм косвенный коэффициент армирования равен:

Коэффициент эффективности косвенного армирования

где 

Приведённая призменная прочность бетона

Площадь сечения смятия площадки (пластинки) определяется из условия прочности на смятие см².

Р
ис. 6 Конструкция стыка колонны

Для квадратной пластинки см, принимаем пластинку размером 8х8х0,5 см.

4.7 Расчёт стыка ригеля с колонной

Р
ис. 7 Стык ригеля с колонной

Рассматриваем вариант бетонированного стыка ригеля с колонной, в этом случае изгибающий момент на опоре воспринимается соединительными стержнями в верхней растянутой зоне и бетоном, заполняющим полость между торцом ригеля и колонной. Принимаем для замоноличивания бетон класса B40, стыковые стержни из арматуры А. Изгибающий момент ригеля на грани колонны М=235,51 кН. Ригель сечением 50х15 см, рабочая высота сечения .

α_>m>=

Из таблицы находим η=0,725. Площадь сечения стыковых надопорных стержней

А_>s>= см²

Принимаем арматуру 432 см².

Определяем длину сварных швов стыковых стержней к закладным деталям ригеля. Усилие растяжения в стыке равно:

кН.

Требуемая суммарная длина сварных швов при высоте катета сварного шва мм, где – диаметр стыковых стержней

Расчётное сопротивление сварных швов составит

где 1,3 вводится для обеспечения надёжной работы сварных швов в случае перераспределения опорных моментов вследствии пластических деформаций. При 4-х стыковых стержнях и двусторонних швах длина каждого шва составит:

см

Конструктивное требование см, принимаем .

Находим длину стыковых стержней (складывается из размера сечения колонны, двух зазоров между колонной и торцами ригелей и 2-х длин сварных швов).

см.

Закладная деталь приваривается к верхним стержням каркаса при изготовлении арматурных каркасов. Приняв ширину закладной детали равной ширине ригеля 150 мм и расчётное сопротивление металла растяжению , находим её толщину.

см, принимаем толщину при этом площадь пластины равна см².

Длина закладной детали принимается из условия приварки верхних и нижних опорных стержней каркасов и не менее см, принимаем см.

5. Расчёт и конструирование отдельного железобетонного фундамента

Фундамент для колонны принимаем сборный, стаканного типа. Размеры фундамента принимаем в зависимости от геологических условий места строительства в разделе «Расчёт оснований и фундаментов»

Принимаем бетон класса B20, арматуру класса А.

Высота фундамента составляет , размеры квадратного фундамента в плане 2,7х2,7 м.

Рабочая высота сечения м.

Давление на грунт от расчётной нагрузки по  ГПС составляет

кПа.

Определяем изгибающие моменты в сечениях

кНм.

Площади сечений арматуры

см²

Принимаем нестандартную сетку с одинаковой в обоих направлениях рабочей арматурой 1510 А с шагом s=14 см. см².

Процент армирования расчётного сечения

6. Расчёт и конструирование монолитного перекрытия

6.1 Компоновка ребристого монолитного перекрытия

Проектируем монолитное ребристое перекрытие с продольными главными балками и поперечными второстепенными балками. При этом пролёт между осями рёбер равен (второстепенные балки располагаем через пролёта главной балки). Предварительно задаёмся размерами сечений балок:

главная балка см. Принимаем см, см, принимаем см.

второстепенная балка см. Принимаем см, см, принимаем см.

6.2 Расчёт многопролётной плиты монолитного перекрытия

Рис. 8 Монолитная плита ребристого перекрытия

6.2.1 Расчётный пролёт и нагрузки

Бетон класса В25 МПа, МПа.

Арматура класса А 6 МПа в сварной рулонной сетке.

Расчётный пролёт плиты равен расстоянию в свету между гранями рёбер в средних пролётах м.

В крайних пролётах при опирании плиты на наружнюю стену м

где м – привязка оси к внутренней грани стенки.

м – величина опирания плиты на стену.

Расчётный пролёт плиты в продольном направлении м.

где 0,25 – ширина главной балки.

Отношение пролётов - плита рассчитывается как работающая в коротком направлении.

Таблица – Нагрузки на 1 м² монолитного перекрытия

№ п/п	Нагрузки	Р^н, кПа	Коэффициент надёжности _>f>	P, кПа
1	Постоянная а) собственный вес плиты (мм) б) вес покрытия пола	1,5 0,85	1,1 1,1	1,65 0,94
	Итого постоянная	2,35		2,59
2	Временная	3,5	1,2	4,2

Полная расчётная нагрузка кПа.

Для расчёта многопролётной плиты выделяем полосу шириной 1 м, при этом расчётная нагрузка на 1 м длины с учётом коэффициента кПа.

Изгибающие моменты балки определяем как для многопролётной неразрезной балки шириной 100 см с пролётами, равными шагу второстепенных балок с учётом перераспределения моментов.

Рис. 9 К расчёту плиты ребристого монолитного перекрытия

В средних пролётах и на средних опорах

кНсм

В первом пролёте

кНсм

На первой промежуточной опоре

кНсм

Средние пролёты плиты окаймлены по контуру монолитно связанными с ними балками и под влиянием возникающих распоров изгибающие моменты уменьшаются на 20%, если условие не соблюдается и момент на средней опоре не надо уменьшать на 20%.

6.2.2 Подбор сечений продольной арматуры

В средних пролётах и на средней опоре см

кНсм

α_>m>=

Из таблицы находим η=0,985

А_>s>= см²

Принимаем сетку 36 А -см²и соответствующую сетку с шагом 100–200 мм в продольном и поперечном направлении.

В первом пролёте

кНсм

α_>m>=

Из таблицы находим η=0,975

А_>s>= см²

Принимаем сетку 56 А -см²и соответствующую сетку с шагом 100–200 мм в продольном и поперечном направлении.

На первой промежуточной опоре. Сечение работает как прямоугольное.

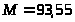кНсм

α_>m>=

Из таблицы находим η=0,983

А_>s>= см²

Принимаем сетку 56 А -см²– две гнутые сетки по 36 в каждой.

6.3 Расчёт многопролётной второстепенной балки

6.3.1 Расчётный пролёт и нагрузки

Расчётный момент второстепенной балки равен расстоянию в свету между главными балками для средних пролётов.

где мм – ширина сечения главной балки.

В крайних пролётах

где мм – величина опирания на стенку второстепенной балки.

Расчётные нагрузки на 1 м длины второстепенной балки.

постоянная от веса плиты и пола кН/м.
постоянная для балки сечением 20х40 кН/м.
с учётом кН/м.
временная с учётом коэффициента кН/м.
полная кН/м.

Р
ис. 10 К расчёту второстепенной балки

6.3.2 Расчётные усилия

Изгибающие моменты балки определяем как для многопролётной неразрезной балки с учётом перераспределения моментов.

В средних пролётах и на средних опорах

кНсм

В первом пролёте

кНсм

На первой промежуточной опоре

кНсм

Отрицательный момент во втором пролёте на расстоянии от опоры определяется по формуле

где - коэффициент определяемый в зависимости от отношения можно принять равным 40% от момента на промежуточной опоре.кНсм.

Поперечные силы:

на крайней опоре кН
на первой промежуточной опоре кН
справа от опоры кН

6.3.3 Определение высоты балки

Высоту сечения определяем по опорному моменту при , поскольку на опоре момент определяют с учётом образования пластического шарнира. Находим .На опоре момент отрицательный – полка ребра в растянутой зоне. Сечение работает как прямоугольное с шириной ребра см.