Класична лінійна регресія

ЛАБОРАТОРНА РОБОТА №1

ТЕМА: КЛАСИЧНА ЛІНІЙНА РЕГРЕСІЯ

Мета: Дослідити метод побудови загальної лінійної регресії та провести аналіз її основних характеристик

Задача: Навчитися отримувати оцінки параметрів загальної лінійної регресії за допомогою 1МНК, визначати статистичні властивості окремих оцінок і моделі в цілому, будувати точковий та інтервальний прогнози за допомогою отриманої моделі. Дослідити альтернативні способи оцінки параметрів лінійної регресії.

Завдання: Для даних з варіанту перевірити гіпотезу про лінійну залежність між змінними Y і X_>1>, X_>2>, X_>3>.

Необхідно:

Побудувати загальну лінійну модель і оцінити коефіцієнти регресії за допомогою оператора 1МНК.

Оцінити значущость окремих коефіціентів регресії і всієї моделі в цілому.

Побудувати точковий та інтервальний прогноз на 3 періоди.

Розрахувати оцінки коефіціентів регресії методом покрокової регресії.

Результати надати у звіті в письмовому вигляді.

Звіт містить дані варіанту, проміжні розрахунки, кінцеві результати кожного етапу дослідження з необхідними поясненнями і висновками

КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ

1. Економетрична модель дає кількісну оцінку кореляційно-регресійного зв'язку між економічними показниками, один чи кілька з яких є залежними (Y), а решта — незалежними змінними (X), тому часто економетричні моделі називаються регресій ними моделями, або просто регресіями.

Припустимо, що істинний зв’язок між Y і Х є лінійним, тобто

_>0> + _>1>X_>1 >+ _>2>X_>2> + ……. + _>m>X_>m>+

або у матричному вигляді:

Y = X + ,

де Y- вектор залежних змінних моделі;

Х – матриця незалежних змінних моделі;

 - вектор відхилень моделі;

 - вектор параметрів моделі

Y = , Х = ,  = ,  =

Розглянемо його оцінку за допомогою лінійної регресійної моделі:

= b_>0> + b_>1>X_>1 >+ b_>2>X_>2> + ……. + b_>m>X_>m>

Оцінки параметрів цієї регресії знаходяться з умови:

(1)

де е – вектор залишків моделі,

.

Продиференціювавши (1) по b_>j> і прирівнявши відповідні часткові похідні по b_>j> до 0, отримаємо такий вираз:

,

домноживши вираз зліва на , отримуємо вираз для знаходження вектора b:

Цей вираз називається основним оператором оцінювання параметрів лінійної моделі, а елементи вектора b є оцінками коефіцієнтів лінійної регресії.

6. Якщо виконуються всі необхідні умови для застосування 1МНК, то оцінки параметрів економетричної моделі мають такі властивості:

1) незміщеності; 3) ефективності;

2) обґрунтованості; 4) інваріантності.

7. Одним з важливих завдань економетричного моделювання — оцінити прогнозне значення залежної змінної за умови, що пояснювальні змінні задані на перспективу. На основі економетричної моделі можна отримати точковий та інтервальний прогнози залежної змінної на перспективу.

8. Незміщена оцінка точкового прогнозу запишеться так:

M[У_>0>(Х_>0>)]=Х_>0> B,

де Х_>0> — заданий рівень пояснюючої змінної на перспективу;

Y_>0> — точковий прогноз залежної функції на основі економетричної моделі.

9. Дисперсія прогнозу дорівнює:

його стандартна помилка :

10. Довірчий інтервал для прогнозних значень:

t_>> - значення t-крітерію при n-m ступенях свободи і рівні значущості .

11. З огляду на залежність між оцінками параметрів моделі та коефіцієнтами парної кореляції можна запропонувати альтернативну оцінку параметрів 1 МНК на основі покрокової регресії, ідея якої базується на існуванні залежності між оцінками параметрів моделі та коефіцієнтами парної кореляції. Ця залежність пропорційна до відношення середньоквадратичних відхилень залежної та незалежної змінних.

12. Опишемо алгоритм пошагової регресії.

Крок 1. Усі вхідні дані стандартизують:

де y* - нормалізована залежна змінна;

х* - нормалізовані незалежні змінні.

Крок 2. Знаходять кореляційну матрицю (матриця парних коефіцієнтів кореляції):

r* = ,

де - парні коефіцієнти кореляції між Y і незалежними змінними Х,

де n – кількість спостережень;

- парні коефіцієнти кореляції між Х_>j> i X_>i> :

.

Крок 3. Вибирають . Відповідну незалежну змінну x_>j> включають в лінійну модель, для якої за допомогою 1МНК знаходять оцінки параметрів:

де  - оцінки параметрів моделі, яка будується на основі нормалізованих даних.

Крок 4. Серед тих, що залишилися, значень вибирається максимальний і в модель вводиться наступна незалежна змінна x_>l>.

.

Оцінюються параметри за допомогою відношення:

r = r_>xy>,

де r – матриця парних коефіцієнтів кореляції між незалежними змінними;

r_>yx> - вектор парних коефіцієнтів кореляції між залежною та незалежними змінними.

Звідси оператор оцінювання параметрів моделі:

Якщо немає обмеження на кількість введених змінних, обчислення виконуються до тих пір, поки не будуть включені всі змінні.

Зв’язок між оцінками параметрів моделі на основі нормалізованих і ненормалізованих змінних запишеться таким чином:

.

13. Тіснота зв’язку загального впливу від незалежних змінних на залежну визначається коефіцієнтами детермінації і множинної кореляції. Коефіцієнт детермінації без урахування числа ступенів свободи

з урахуванням ступенів свободи:

.

14. Коефіцієнт детермінації показує, на скільки процентів варіація залежної змінної визначається варіацією пояснюючих (незалежних) змінних.

Коефіцієнт кореляції є інваріантною оцінкою коефіцієнта детермінації. Він характеризує тісноту зв'язку між залежною і пояснювальними змінними. Визначається як корінь квадратний від R².

15. Оскільки коефіцієнти детермінації і кореляції є вибірковими характеристиками, то їх числові значення також перевіряються на значущість згідно зі статистичними гіпотезами. Для перевірки значущості коефіцієнта кореляції використовується t-критерій.

Нульова гіпотеза: значення коефіцієнту кореляції несуттєво відрізняється від 0.

Розрахункове значення критерію визначається як:

Якщо розрахункове значення цього критерію t не менше за критичне (табличне) t_>таб> при вибраному рівні довіри  і ступені свободи n - m, тобто t t_>таб> , нульова гіпотеза відхиляється і відповідний коефіцієнт кореляції є достовірним.

16. Гіпотеза про істотність зв'язку між залежною і незалежною змінними може бути перевірена з допомогою F-критерію. Нульова гіпотеза: всі коефіцієнти регресії несуттєво відрізняються від 0, тобто Н_>0>: b_>0> = b_>1> = …….. =b_>m> = 0.

Розрахункове значення F-критерію визначається за формулою:

або в альтернативному запису:

Розрахункове значення порівнюється з табличним F_>таб >_> >при n-m i m-1ступенях свободи та вибраному рівні довіри . Якщо F  F_>таб> , нульова гіпотеза відхиляється і істотність моделі підтверджується, в протилежному випадку – відхиляється.

17. Гіпотезу про значущість кожного з параметрів b_>j> економетрічної моделі можна виконати за допомогою t-крітерію. Нульова гіпотеза: b_>j>_> >несуттєво відрізняються від 0, тобто H_>0>: b_>j> = 0. Розрахункове значення t-критерію:

де c_>jj> – діагональний елемент j-ї строки (стовпця) матриці ,

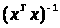- стандартна помилка оцінки j-го параметра моделі.

Якщо t t_>таб> , нульова гіпотеза відхиляється і відповідний коефіцієнт регресії є достовірним.

18. На основі t-критерію і стандартної помилки будуються граничні інтервали для оцінок параметрів моделі:

де t_>> - табличне значення t-статистики з рівнем довіри  та ступенями свободи n-m.

ПРИКЛАД ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ

Нехай маємо змінні:

- середньомісячна зарплата, ум. од.;

- продуктивність праці, ум. од.;

- фондомісткість продукції ум. од;

- виконання норми виробітку,%

Гіпотеза, що пропонується для перевірки - середньомісячна зарплата лінійно залежить від продуктивності праці, фондомісткості продукції та виконання норми виробітку.

Позначимо Y - середньомісячна зарплата, X_>1> - продуктивність праці, X_>2> - фондомісткість продукції, X_>3> - виконання норми виробітку/

Вихідні дані наведено в таблиці.

номер цеху	середньомісячна з/п,Y	Продуктивність праці, X>1>	ФондомісткістьX>2>	Норма виробітку, X>3>
1	45	265	0,2	130
2	42	236	0,04	127
3	50	257	0,3	151
4	55	279	0,2	149
5	40	226	0,1	140
6	70	350	0,1	141
7	56	278	0,25	152
8	57	262	0,03	188
9	55	269	0,15	120
10	53	250	0,32	126

Матриця Х доповнюється стовбцем одиниць для врахування коефіцієнта регресії b_>0>:

1. Оцінимо параметри регресії за допомогою 1МНК.

Підготуємо необхідні проміжні матриці:

Використовуючи оператор оцінювання МНК, отримуємо

 Рівняння регресії має вигляд:

Y = -23,83+0,23X_>1>+9,018X_>2>+0,097X_>3>

Ця модель має бути проаналізована на значущість в цілому (2), а також на значущість кожного коефіцієнта регресії зокрема (3).

2. Перевірка значущості моделі

Значущість всієї моделі в цілому будемо проводити для рівня значущості =0,05 за допомогою F-крітерія при (m-1) і (n-m) ступенях свободи. Розрахункове значення F-критерію розраховується по формулі:

де ,

Y – спостеріганні значення фактора (вихідні дані),

n – число спостережень,

m – число оцінюваних параметрів.

Нульова гіпотеза для перевірки значущості моделі: Н_>0>: b_>0> = b_>1> = …… = b_>m>= 0.

Проведемо необхідні попередні розрахунки.

Використовуючи вихідну матрицю Х і побудовану модель, отримуємо розрахункові Yp:

Y_>p> = X*B^T і залишки е = Y - Y_>p> :

Сума квадратів відхилень значень регресії від середнього та сума залишків дорівнює:

583,5752 ,

Табличне значення для (m-1), (n-m) F-критерію (0,95) = 4,76. Оскільки F_>p>>F_>табл >, модель можна вважати статистично значимою. (нульова гіпотеза відхиляється).

Далі оцінюєтья значущість кожного з параметрів b_>j>.за допомогою t-статистики.

3. Оцінка значущості окремих коефіцієнтів регресії.

Гіпотезу про значущість кожного з параметрів b_>j> економетрічної моделі можна виконати за допомогою t-крітерію. Нульова гіпотеза, найбільш поширена притестуванні економетричної моделі - bj_> >несуттєво відрізняються від 0, тобто H_>0>: b_>j> = 0. Поширеність такої постанови нульової гіпотези – в тому, що якщо вона підтверджується, то це має означати, що відповідний X_>j> статистично незначущо впливає на Y, його вплив з високою вірогідністю дорівнює 0, залежності між Y та Х практично немає і відповідна змінна повинна бути виключена з моделі. Виключенням є випадок, коли при незначущому b_>j> залежність між X і Y таки існує, але нелінійна. В цьому випадку треба змінити специфікацію моделі (надати їй іншу аналітичну форму).

Розрахункове значення t-критерію:

де S_>bj> – стандартна помилка коефіцієнта b_>j>,

c_>jj> – діагональний j-й елемент матриці С=

Визначимо значення стандартних помилок коефіцієнтів регресії S_>bj> як корінь з дисперсії коефіцієнта b_>j>:

Для отримання оцінок дисперсії D_>j> розрахуємо дисперсійно-коваріаційну матрицю (іноді її називають коваріаційною).

Розраховується вона за формулою

,

де - дисперсія залишків

Матрицю С= ми маємо.

, де

n – кількість спостережень, n=10

m – кількість оцінюваних параметрів моделі, m=4.

Стандартне відхилення залишків = 4,912352.

Отримуємо:

=

На діагоналі коваріаційної матриці отримуємо дисперсії коефіцієнтів регресії b_>j>:

D(b_>0>) = 318,9421,

D(b_>1>)=0,002358,

D(b_>2>)=272,2121,

D(b_>3>)=0,007489

Визначимо значення стандартних помилок коефіцієнтів регресії S_>bj>:

S_>b0> = = 17,85895,

S_>b1> == 0,048839,

S_>b2> = = 16,49885,

S_>b3> == 0,086537

17,85895

0,048839

16,49885

0,086537

S_>b> =

Розрахункове значення t-статистики отримуємо для кожного коефіцієнта:

t_>b0> = b_>0> / S_>b0> = -23,83/ 17,85895 = -1,33433 і т. п.

-1,33433

4,658181

0,546609

1,121298

t_>p> =

Розрахункові значення t-статистики порівнюються за абсолютною величиною з табличним t_>10-4 >= 1,943. Параметр вважається статистично значимим (нульова гіпотеза не підтверджується), якщо

Це означає, що в нашому випадку тільки b_>1> є статистично значущим і суттєво впливає на модель.

Довірчі інтервали для оцінок регресії будуються за формулою:

b>0> =-23,829834,699

b>1> =0,22750,0949

b>2> =9,01842332,0573

b>3> =0,0970340,1681

:

4. Якість побудованої моделі можна визначити за допомогою коефіцієнта детермінації:

,

Його значення показує, що на 85,8073% варіацію змінної Y можна пояснити варіацією пояснювальних змінних Х.

5. Тіснота зв’язку між Y і X для множинної регресії визначається за допомогою коефіцієнтів кореляції трьох типів:

коефіцієнта множинної кореляції R (визначається як корінь з коефіцієнта детермінації) – показує тісноту зв’язку між Y і всією множиною пояснювальних зміннихX (1 на модель) ;

парних коефіцієнтів кореляції r, що знаходяться в кореляційній матриці r* і характеризують тісноту зв’язку між Y та окремим X_>j>_> >._> >Вони діляться на два типи:

а) парні коефіцієнти кореляції між Y та окремим X_>j>_> >

б) парні коефіцієнти кореляції між окремими X_>k> і X_>j>_> > r_>XkXj>_> > _> >(їх для моделі існує m*m);

частинних коефіцієнтів кореляції, що також характеризують тісноту зв’язку між Y та окремим X_>j>_> >, але при умові, що інші незалежні змінні сталі, тобто їх варіація не впливає на залежність між Y та Х:

де R_>kj> – алгебраїчне доповнення до (j,k)-го елемента кореляційної матриці r;

R_>kk> та R_>jj> – відповідні діагональні елементи цієї матриці.

За вимогами роботи треба розрахувати коефіцієнт множинної кореляції R:

R =

де R² – коефіцієнт детермінації;

0,926322 – тіснота зв’язку між Y і X для нашої регресії є досить великою.

Його значущість перевіряється також за допомогою t-статистики (нульова гіпотеза – R незначущо відрізняється від 0). В цьому випадку розрахункове значення крітерію визначається за формулою:

Розрахункое значення t-статистики порівнюється за абсолютною величиною з табличним t_>10-4 >= 1,943. Оскільки розрахункове значення більше, коефіцієнт кореляції є статистично значущим.

4. Побудова прогнозу по регресійній моделі

Точковий прогноз. Задані прогнозні Х_>01>, Х_>02>, Х_>03> для певного 0-го періоду. Прогнозне значення Y_>0 >для цього періоду розраховується по формулі:

Y_>0> =

Якщо Х_>01> = 252, Х_>02>=0,35, а Х_>03> = 128 (задаються дослідником або визначаються по продовженню тенденції їх зміни), то точковий прогноз на 0-й період складе:

Y_>0> = = -23,83+0,23 * 252 + 9,02 0,35 + 0,10*128 = 49,07704,

чи в матричному вигляді:

Y = B^Т*X_>0>=49,07704

Де В – матриця оцінок параметрів моделі. Його стандартна похибка складає

16,60574

Інтервальний прогноз визначається як

=49,07704 1,943*24,1312*= =49,07704 11,58627