Взаимозаменяемость продовольственных продуктов: масла животного и масла растительного. Их потребление
тема: Взаимозаменяемость продовольственных продуктов: масла животного и масла растительного. Их потребление.
Этап 1 Постановочный
Целью этой работы является изучение взаимозаменяемости продовольственных товаров: масла животного и масла растительного. А затем построение модели, которую можно было бы использовать для прогнозирования взаимозаменяемости товаров.
Этап 2 Априорный
Изучив сложившуюся ситуацию на рынке продовольственных товаров, я пришла к выводу, что взаимозаменяемость вышеуказанных продуктов зависит от цент на эти продукты, от национальных предпочтений, от удаленности от производства, сезонных особенностей употребления этих продуктов.
Итак, результативный признак Y – потребление животного масла кг., фактор Х – потребление растительного масла кг.
Этап 3 Информационный
Для изучения влияния именно фактора Х (потребление растительного масла), постараемся отобрать в выборку однородные участки, т.е. с примерно одинаковыми характеристиками, и за один и тот же период времени.
В выборку отобрано 55 регионов РФ, расположенных в Южном федеральном округе, Приволжском федеральном округе, Уральском федеральном округе, Сибирском федеральном округе и Дальневосточном федеральном округе на январь – февраль 2007 года.
Источник статистических данных – сайт Госкомстата РФ, распечатки прилагаются.
|
№ |
У (потребление животного масла), кг |
Х (потребление растительного масла), кг |
|
Республика Адыгея |
50,8 |
138,4 |
|
Республика Дагестан |
50,8 |
147,5 |
|
Республика Ингушетия |
46,3 |
113 |
|
Кабардино-Балкарская Республика |
65,1 |
167 |
|
Республика Калмыкия |
45,5 |
105,6 |
|
Карачаево-Черкесская Республика |
66,9 |
167,2 |
|
Республика Северная Осетия - Алания |
76,1 |
198,7 |
|
Краснодарский край |
83,1 |
252,1 |
|
Ставропольский край |
63,9 |
197 |
|
Астраханская область |
108,4 |
217,8 |
|
Волгоградская область |
91,5 |
243,1 |
|
Ростовская область |
86,5 |
242,1 |
|
Республика Башкортостан |
105,6 |
261,3 |
|
Республика Марий Эл |
64,4 |
149,4 |
|
Республика Мордовия |
59,5 |
151,1 |
|
Республика Татарстан |
118,5 |
266,8 |
|
№ |
У (потребление животного масла), кг |
Х (потребление растительного масла), кг |
|
Удмуртская Республика |
68,1 |
172,7 |
|
Чувашская Республика |
55,9 |
149,7 |
|
Пермский край |
118,9 |
294,5 |
|
Кировская область |
53 |
168,3 |
|
Нижегородская область |
80,2 |
227,2 |
|
Оренбургская область |
74,4 |
209,6 |
|
Пензенская область |
82,8 |
183,8 |
|
Самарская область |
85,2 |
237,1 |
|
Саратовская область |
90,5 |
190,3 |
|
Ульяновская область |
80,3 |
196,7 |
|
Курганская область |
68,6 |
194 |
|
Свердловская область |
104,2 |
285,1 |
|
Тюменская область |
173,3 |
455 |
|
Ханты-Мансийский авт.округ-Югра |
221,4 |
547,8 |
|
Ямало-Ненецкий авт. округ |
195,9 |
546,1 |
|
Челябинская область |
87 |
230,8 |
|
Республика Алтай |
63,7 |
154,7 |
|
Республика Бурятия |
80,2 |
190,4 |
|
Республика Тыва |
41 |
88 |
|
Республика Хакасия |
66,9 |
171,8 |
|
Алтайский край |
66,4 |
202,9 |
|
Забайкальский край |
79,9 |
167,3 |
|
Агинский Бурятский авт. округ |
73,2 |
162,8 |
|
Красноярский край |
103,2 |
276,9 |
|
Иркутская область |
89,5 |
210,3 |
|
Усть-Ордынский Бурятский авт. округ |
43,7 |
82,7 |
|
Кемеровская область |
93,3 |
258,4 |
|
Новосибирская область |
90,5 |
229,9 |
|
Омская область |
102,7 |
272,3 |
|
Томская область |
107 |
273,5 |
|
Республика Саха (Якутия) |
116,6 |
254,6 |
|
Камчатский край |
90,8 |
293,2 |
|
Приморский край |
73,9 |
208,3 |
|
Хабаровский край |
83,5 |
294 |
|
Амурская область |
56,4 |
185,2 |
|
Магаданская область |
99 |
290,6 |
|
Сахалинская область |
113,4 |
372,2 |
|
Еврейская автономная область |
65,5 |
174 |
|
Чукотский авт. округ |
108,2 |
285,8 |
Предварительный анализ статистических данных
Основные расчёты были проведены с помощью программы MathCAD (распечатки прилагаются).
(Или: Для удобства вычислений в ходе решения будем достраивать исходную таблицу данных до вспомогательной таблицы (см. расчетную таблицу ниже), округляя и занося в неё промежуточные результаты).
Поле корреляции и линия регрессии
Сначала построим поле корреляции – точки с координатами (х>i>, у>i>), и по их расположению сформулируем предположение о связи Y(потребление животного масла) и X(потребление растительного масла).
Визуальный анализ полученного поля корреляции показывает, что точки располагаются вдоль некоторой воображаемой возрастающей прямой линии, причём достаточно плотно, слабо рассеиваясь около неё.
Т.е. можно сказать, что прослеживается тесная прямая (положительная) зависимость, т.к. чем больше потребление растительного масла, тем больше потребление животного масла, которое зависит от сезонных особенностей.
Также можно заметить, что варьирование (дисперсия) потребление животного масла сильнее при малом потреблении растительного масла, а при большем потреблении – дисперсия потребления животного масла мала. Следовательно, можно предположить, что в модели будет гетероскедастичность.
Проверим наши предположения аналитически, с помощью расчётов на следующих этапах.
Основные характеристики выборки
Средние значения:
и
.
Стандартные отклонения:
и
(где
и
).
Итак, в данной выборке рассматриваются взаимозаменяемость потребления растительного масла в среднем на 225,275 кг. со стандартным отклонением 91,273 кг., потребления животного масла в среднем составила 86,02 кг. со стандартным отклонением 33,777 кг.
Линейный коэффициент корреляции:
(где
).
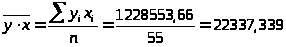Это подтверждает сделанные ранее выводы.
Т.к.
,
то взаимозаменяемость животного
масларастительного
масла действительно можно считать
линейной. Эта линейная зависимость
положительна. Теснота связи очень
сильная. А значит, линейная парная
регрессионная модель вполне подойдёт
для исследования и описания
взаимозаменяемость животного
масларастительного
масла.
Этап 4 Спецификация и параметризация
Линейная парная регрессионная модель
На основе предыдущих этапов можем с большой уверенностью предположить, что взаимозаменяемость животного масла и растительного масла – линейна.
Тогда для моделирования используем
линейную парную регрессионную модель
для генеральной совокупности.
Для выборки модель также линейна:
.
Найдём объяснённую часть модели
- линейное уравнение регрессии
по выборке:
.
Для этого нужно найти коэффициенты
регрессии а>0>
и а>1>,
являющиеся оценками параметров >0>
и >1>
линейной модели. А затем оценим случайную
составляющую
с помощью остатков e>i>
и проверим выполнение для них предпосылок
МНК.
Этап 5 Идентификация
Для построения модели используем классический подход - метод наименьших квадратов МНК.
Из системы нормальных уравнений:
находим коэффициенты регрессии
а>0>
и а>1>.
Все необходимые числовые значения
рассчитаны ранее (см. расчетную таблицу),
подставим их в систему нормальных
уравнений:
ему
нормальных уравнений: бюджет льуплений
от налога на прибыль предприятий о с
увеличением размера среднемесячной
зарплаты Х н
и решим её относительно а>0>,
а>1>.
Получим коэффициенты
регрессии: а>0>=6,622
и
.
Итак, уравнение
регрессии имеет вид:
.
Коэффициент а>0>=6,622 формально интерпретируется как взаимозаменяемость потребление животного масла, равным нулю, т.е. при х=0. Это вполне имеет смысл. Т.о., взаимозаменяемость животного масла в среднем в январе – декабре 2007 г. составляла 6,622 кг.
А коэффициент
показывает, что полученная линейная
связь взаимозаменяемости потребления
животного масла (результативного
признака Y)
и растительного масла (фактора Х) –
положительна, то есть при увеличении
потребления растительного масла на 1
кг. от среднего значения, то потребление
животного масла вырастит на 0,352 от
среднего значения.
В декартовой системе координат ХОУ на поле корреляции строим и график линии регрессии по найденному уравнению.
Действительно, видим, что точки поля корреляции плотно расположены вдоль прямой регрессии. А значит, построенная линейная модель хорошо описывает стат. данные. Проведём подробный анализ её качества.
Этап 6 Верификация
Линейный коэффициент корреляции
Вычислим его по другой формуле, проверим правильность расчётов:
- совпадает с вычисленным ранее
(небольшое различие – из-за округления).
Коэффициент детерминации
По свойству:
.
Он показывает, что вариация результативного признака Y (потребление животного масла) на 90,6% объясняется вариацией фактора X (потребление растительного масла). То есть потребление животного масла на 78,6% обусловлены взаимозаменяемостью растительного масла. А в остальном – на 9,4% потребления животного масла обусловлено колебаниями и изменениями других факторов и условий.
Т.е., подтвердилось предположение о взаимозаменяемости потребления животного масла и растительного масла.
Средний коэффициент эластичности
Для линейной регрессии:
.
Средний коэффициент эластичности показывает, что в среднем при увеличении потребления животного масла на 1% от своего среднего значения, потребление растительного масла увеличится в среднем на 0,923% от своего среднего значения.
Эластичность взаимозаменяемых
товаров достаточно велика, что вполне
согласуется со сложившейся ситуацией
на рынке продовольствия в РФ. Чем выше
продажа растительного масла, тем сильнее
и заметнее растет продажа животного
масла. Проверим правильность вычислений:
(см. расчётную табл. - действительно).
Оценка статистической значимости коэффициентов регрессии и коэффициента корреляции
Оценим статистическую значимость полученных коэффициентов регрессии а>0> и а>1>, коэффициента корреляции r>ух> с помощью t-критерия Стьюдента на уровне значимости =0,05.
Эта проверка проводится по единой схеме, с помощью гипотез.
Выдвигается нулевая гипотеза
Н>0> о случайной
природе полученного коэффициента, о
незначимом его отличии от нуля, то есть
гипотеза Н>0>
состоит в том, что коэффициент=0.
Альтернативная ей гипотеза Н>1
>состоит в том, что
неслучайно, то есть полученный коэффициент
статистически значим. Чтобы опровергнуть
гипотезу Н>0>
и подтвердить гипотезу Н>1
>должно выполняться
неравенство
на уровне значимости
и с (n–2)
степенями свободы, где n
– количество наблюдений, уровень
значимости – вероятность совершить
ошибку, отвергнув гипотезу Н>0>,
когда она верна.
Для а>1>:
Н>0>: а>1>=0,
Н>1>:
.
Рассчитаем стандартную ошибку
коэффициента регрессии а>1>
–
.
Потребуется сделать промежуточные
вычисления: подставляя фактические
значения х>i>
в уравнение регрессии найдем смоделированные
значения
,
затем вычислим разность между фактическими
и смоделированными значениями, т.е.
остатки
,
затем возведём остатки в квадрат е>i>2
и просуммируем; результаты представлены
в расчетной таблице. Теперь подставим
необходимые данные в формулу для расчёта
:
и t-статистики
по модулю:
.
Затем сравним наблюдаемое
значение
с табличным значением t-критерия
Стьюдента. Табличное значение по таблице
распределения Стьюдента на уровне
значимости =0,05
с n–2=55-2=53
степенями свободы:
t>табл>=2,01.
Наблюдаемое значение t-статистики
превышает табличное значение t-критерия:
22 > 2,01, то
есть выполнено неравенство
,
а значит, гипотеза Н>0>
о случайной природе полученного
коэффициента отвергается и принимается
альтернативная ей гипотеза Н>1>,
свидетельствующая в 95% случаев о>
>статистической значимости
полученного коэффициента регрессии
а>1>.
Т.о., можно считать, что взаимозаменяемость
товаров подтвердилась и статистически
установлена.
Для а>0>:
Н>0>: а>0>=0,
Н>1>:
.
Рассчитаем стандартную ошибку
коэффициента регрессии а>0>>
>–
.
Все необходимые цифры уже имеются в
расчетной таблице, подставим эти данные
в формулу:
,
а затем рассчитаем t-статистику
по модулю:
.
Сравнивая рассчитанное значение с табличным значением t-критерия Стьюдента на уровне значимости =0,05 с n–2=55-2=53 степенями свободы: t>табл>=2,01,где 2<t>a>>0>< 3 (t>табл > >t>a>>0>) можно сделать вывод, что коэффициент регрессии а>0>> >можно признать статистически значимым в 90% случаев.
Для r>ух>:
Н>0>: r>ух>=0,
Н>1>:
.
Для этого рассчитаем стандартную
ошибку коэффициента корреляции r>ух>>
>–
:
и t-статистику
по модулю:
.
Сравнивая рассчитанное значение с табличным значением t-критерия Стьюдента на уровне значимости =0,05 с n–2=55-2=53 степенями свободы: t>табл>=2,01, можно сделать вывод о> >статистической значимости полученного коэффициента корреляции r>ух>> >в 95% случаев, предполагаемая взаимозаменяемость товаров подтвердилась.
Проверим правильность вычислений:
,
действительно 2222,7.
Доверительные интервалы для параметров регрессионной модели >0> и >1>
Доверительный интервал для >0>
с надежностью =1-:
.
Выбрав уровень значимости =0,05,
получаем надежность =0,95.
Все необходимые цифровые значения уже
рассчитаны ранее, тогда
,
откуда получаем (0,4312; 12,813).ыберемрительной
вероятностью ров регрессионной модели
Доверительный интервал для >1>
с надежностью =1-:
.
При выбранной надежности =0,95:
,
откуда (0,32; 0,384).
Таким образом, с надежностью 95% можно утверждать, что истинное значение параметра >0> будет заключено в пределах от 0,4312 до 12,813, а истинное значение параметра >1> - в границах от 0,32 до 0,384.
Следует отметить, что доверительные
интервалы узкие, т.к. значения стандартных
ошибок
и
малы. А это подтверждает, что другие
факторы оказывают несущественное
влияние на покупательскую способность
товаров. Основным фактором является
выбранный фактор Х – замена растительным
маслом. Значит, точность модели будет
вполне приемлемой.
Оценка качества уравнения регрессии в целом
F-критерий Фишера
Выдвигается нулевая гипотеза
Н>0> о
статистической незначимости уравнения
регрессии. Альтернативная ей гипотеза
Н>1 >о
статистической значимости. Чтобы
опровергнуть гипотезу Н>0>
и подтвердить гипотезу Н>1
>должно выполняться
неравенство
.
Рассчитаем наблюдаемое значение
F-критерия
(воспользуемся свойством для линейной
парной регрессии):
.
Табличное значение по таблице
распределения Фишера на уровне значимости
=0,05
с k>1>=1
и k>2>=n–2=23-2=21
степенями свободы:
F>табл>=4,03.
Наблюдаемое значение F–критерия
превышает табличное: 510,83 >
4,03, то есть выполнено неравенство
,
а значит, гипотеза Н>0>
о случайной природе полученного уравнения
регрессии отклоняется в пользу гипотезы
Н>1>,
свидетельствующей в 95% случаев о>
>его статистической
значимости и взаимозаменяемости товаров.
Уравнение по данным выборки можно
признать надежным и значимым, доказывающим
наличие исследуемой зависимости.
Оценка аппроксимации модели
Потребуется сделать промежуточные
вычисления: остатки е>i>
разделим на фактические значения у>i>,
полученные частные от этих делений
возьмем по модулю
и просуммируем; результаты представлены
в расчетной таблице.
Средние ошибки аппроксимации:
,
.
Ошибки почти совпадают и равны 25%.
В среднем смоделированные значения взаимозаменяемость животного масла отклоняются от фактических на 9-12%. Подбор модели к фактическим данным можно оценить как не точный, так как средняя ошибка аппроксимации превышает 20%.
Но, учитывая высокое качество модели и сильную линейную зависимость между Y (потребление животного масла) и Х (потребление растительного масла), эту модель можно использовать для прогнозирования с осторожностью.
Т.к. большую погрешность. Только при этом следует помнить, что в некоторых случаях прогнозы могут быть вполне точны, а в некоторых содержать немаленькую погрешность, до 12% в среднем.
Этап 7 Выводы, предложения. Прогнозирование
Прогнозирование по полученному уравнению регрессии
Полученные оценки уравнения регрессии не позволяют использовать его для качественного прогноза взаимозаменяемости товаров. Как уже говорилось, точность модели невысока. Можно её использовать лишь для того, чтобы составить приблизительное мнение о взаимозаменяемости и только в рассмотренный период.
Пусть прогнозное значение фактора
х=300 кг (при
этом реальное потребление животного
масла в январе-феврале 2007 г. - 100 кг.)
Точечный прогноз:
кг.
Как видим, прогноз непригоден, сильно завышен.
Пусть прогнозное значение фактора
х=90 кг (при
этом реальная потребление животного
масла в январе-феврале 2007 г. - 43 кг.))
Точечный прогноз:
кг.
Как видим, в этом случае прогноз занижен, но более-менее соответствует действительности, особенно если учесть, что его погрешность 9-12%. Можно сделать поправку на эту погрешность, и тогда получим 32,902 кг., тоже не равно реальному значению. Реальное значение 43 кг., оказалось как раз между ними. Но как это угадать при неизвестном значении Y (продажа животного масла)?
Доверительный интервал для
средней продажи животного масла при
условии, при условии взаимозаменяемости
растительным маслом, х=90
км с надежностью =0,95:
,
где стандартная ошибка для
средних значений:
.
И даже этот доверительный интервал продаж животного масла от 34,242 до 42,362 кг. не включает в себя реального значения, занижает прогноз.
Доверительный интервал для
индивидуальной продажи животного масла
при условии, при условии взаимозаменяемости
растительным маслом, х=90
кг с надежностью =0,95:
,
где стандартная ошибка для индивидуальных значений:
.
В этот интервал продажи животного масла попало. Но интервал получился очень широким.
Таким образом, если продажа растительного масла равнялась 90 кг, то продажа животного масла в январе - феврале 2007 г. могла составлять от 15,374 до 61,23 кг. Этот интервал определяет границы, за пределами которых могут оказаться не более 5% значений цен, которые могли быть зафиксированы для взаимозаменяемых товаров.
Выводы, сделанные ранее о прогнозах по этой модели подтвердились. Ни точечный, ни интервальный прогноз не отличаются точностью, и с трудом пригодны для практического использования в отдельных случаях.
Расчетная таблица
-
№
x>i>2
y>i> x>i>
y>i>2
e>i>
e>i>2
Республика Адыгея
19154,56
7030,72
2580,64
4,5388
20,601
0,08934646
Республика Дагестан
21756,25
7493
2580,64
7,742
59,939
0,15240157
Республика Ингушетия
12769
5231,9
2143,69
0,098
0,010
0,00211663
Кабардино-Балкарская Республика
27889
10871,7
4238,01
0,306
0,094
0,00470046
Республика Калмыкия
11151,36
4804,8
2070,25
-1,7068
2,913
0,03751209
Карачаево-Черкесская Республика
27955,84
11185,68
4475,61
-1,4236
2,027
0,02127952
Республика Северная Осетия - Алания
39481,69
15121,07
5791,21
0,4644
0,216
0,0061025
Краснодарский край
63554,41
20949,51
6905,61
12,2612
150,337
0,14754753
Ставропольский край
38809
12588,3
4083,21
12,066
145,588
0,18882629
Астраханская область
47436,84
23609,52
11750,56
-25,1124
630,633
0,23166421
Волгоградская область
59097,61
22243,65
8372,25
0,6932
0,481
0,00757596
Ростовская область
58612,41
20941,65
7482,25
5,3412
28,528
0,06174798
Республика Башкортостан
68277,69
27593,28
11151,36
-7,0004
49,006
0,06629167
Республика Марий Эл
22320,36
9621,36
4147,36
-5,1892
26,928
0,08057764
Республика Мордовия
22831,21
8990,45
3540,25
0,3092
0,096
0,00519664
Республика Татарстан
71182,24
31615,8
14042,25
-17,9644
322,720
0,15159831
Удмуртская Республика
29825,29
11760,87
4637,61
-0,6876
0,473
0,01009692
Чувашская Республика
22410,09
8368,23
3124,81
3,4164
11,672
0,06111628
Пермский край
86730,25
35016,05
14137,21
-8,614
74,201
0,07244743
Кировская область
28324,89
8919,9
2809
12,8636
165,472
0,24270943
Нижегородская область
51619,84
18221,44
6432,04
6,3964
40,914
0,07975561
Оренбургская область
43932,16
15594,24
5535,36
6,0012
36,014
0,08066129
Пензенская область
33782,44
15218,64
6855,84
-11,4804
131,800
0,13865217
Самарская область
56216,41
20200,92
7259,04
4,8812
23,826
0,05729108
Саратовская область
36214,09
17222,15
8190,25
-16,8924
285,353
0,18665635
Ульяновская область
38690,89
15795,01
6448,09
-4,4396
19,710
0,05528767
Курганская область
37636
13308,4
4705,96
6,31
39,816
0,09198251
№
x>i>2
y>i> x>i>
y>i>2
e>i>
e>i>2
Свердловская область
81282,01
29707,42
10857,64
2,7772
7,713
0,02665259
Тюменская область
207025
78851,5
30032,89
-6,518
42,484
0,03761108
Ханты-Мансийский авт. округ-Югра
300084,84
121282,92
49017,96
-21,9524
481,908
0,09915266
Ямало-Ненецкий авт. округ
298225,21
106980,99
38376,81
2,9492
8,698
0,01505462
Челябинская область
53268,64
20079,6
7569
0,8636
0,746
0,00992644
Республика Алтай
23932,09
9854,39
4057,69
-2,6236
6,883
0,04118681
Республика Бурятия
36252,16
15270,08
6432,04
-6,5572
42,997
0,0817606
Республика Тыва
7744
3608
1681
-3,402
11,574
0,08297561
Республика Хакасия
29515,24
11493,42
4475,61
0,1956
0,038
0,00292377
Алтайский край
41168,41
13472,56
4408,96
11,6428
135,555
0,17534337
Забайкальский край
27989,29
13367,27
6384,01
-14,3884
207,026
0,1800801
Агинский Бурятский авт. округ
26503,84
11916,96
5358,24
-9,2724
85,977
0,12667213
Красноярский край
76673,61
28576,08
10650,24
0,8908
0,794
0,00863178
Иркутская область
44226,09
18821,85
8010,25
-8,8524
78,365
0,0989095
Усть-Ордынский Бурятский авт. округ
6839,29
3613,99
1909,69
-7,9676
63,483
0,18232494
Кемеровская область
66770,56
24108,72
8704,89
4,2788
18,308
0,04586066
Новосибирская область
52854,01
20805,95
8190,25
-2,9532
8,721
0,03263204
Омская область
74147,29
27965,21
10547,29
-0,2284
0,052
0,00222395
Томская область
74802,25
29264,5
11449
-4,106
16,859
0,03837383
Республика Саха (Якутия)
64821,16
29686,36
13595,56
-20,3588
414,481
0,17460377
Камчатский край
85966,24
26622,56
8244,64
19,0284
362,080
0,20956388
Приморский край
43388,89
15393,37
5461,21
6,0436
36,525
0,08178078
Хабаровский край
86436
24549
6972,25
26,61
708,092
0,31868263
Амурская область
34299,04
10445,28
3180,96
15,4124
237,542
0,2732695
Магаданская область
84448,36
28769,4
9801
9,9132
98,272
0,10013333
Сахалинская область
138532,84
42207,48
12859,56
24,2364
587,403
0,21372487
Еврейская автономная область
30276
11397
4290,25
2,37
5,617
0,03618321
Чукотский авт. округ
81681,64
30923,56
11707,24
-0,9764
0,953
0,00902403
Сумма
3256815,82
1228553,66
469716,49
0
5938,511
5,036
Проверка выполнения предпосылок МНК
Предпосылка 2. О гомоскедастичности остатков.
На Этапе 3 по полю корреляции и характеру стат. данных было сделано предположение о наличии гетероскедастичности. Проверим его с помощью теста Голдфельда-Квандта.
Упорядочиваем выборку по возрастанию фактора Х.
|
№ |
У (продажа животного масла) |
Х (продажа растительного масла) |
|
Усть-Ордынский Бурятский авт. округ |
43,7 |
82,7 |
|
Республика Тыва |
41 |
88 |
|
Республика Калмыкия |
45,5 |
105,6 |
|
Республика Ингушетия |
46,3 |
113 |
|
Республика Адыгея |
50,8 |
138,4 |
|
Республика Дагестан |
50,8 |
147,5 |
|
Республика Марий Эл |
64,4 |
149,4 |
|
Чувашская Республика |
55,9 |
149,7 |
|
Республика Мордовия |
59,5 |
151,1 |
|
Республика Алтай |
63,7 |
154,7 |
|
Агинский Бурятский авт. округ |
73,2 |
162,8 |
|
Кабардино-Балкарская Республика |
65,1 |
167 |
|
Карачаево-Черкесская Республика |
66,9 |
167,2 |
|
Забайкальский край |
79,9 |
167,3 |
|
Кировская область |
53 |
168,3 |
|
Республика Хакасия |
66,9 |
171,8 |
|
Удмуртская Республика |
68,1 |
172,7 |
|
Еврейская автономная область |
65,5 |
174 |
|
Пензенская область |
82,8 |
183,8 |
|
Амурская область |
56,4 |
185,2 |
|
Саратовская область |
90,5 |
190,3 |
|
Республика Бурятия |
80,2 |
190,4 |
|
Курганская область |
68,6 |
194 |
|
Ульяновская область |
80,3 |
196,7 |
|
Ставропольский край |
63,9 |
197 |
|
Республика Северная Осетия - Алания |
76,1 |
198,7 |
|
Алтайский край |
66,4 |
202,9 |
|
№ |
У (продажа животного масла) |
Х (продажа растительного масла) |
|
Приморский край |
73,9 |
208,3 |
|
Оренбургская область |
74,4 |
209,6 |
|
Иркутская область |
89,5 |
210,3 |
|
Астраханская область |
108,4 |
217,8 |
|
Нижегородская область |
80,2 |
227,2 |
|
Новосибирская область |
90,5 |
229,9 |
|
Челябинская область |
87 |
230,8 |
|
Самарская область |
85,2 |
237,1 |
|
Ростовская область |
86,5 |
242,1 |
|
Волгоградская область |
91,5 |
243,1 |
|
Краснодарский край |
83,1 |
252,1 |
|
Республика Саха (Якутия) |
116,6 |
254,6 |
|
Кемеровская область |
93,3 |
258,4 |
|
Республика Башкортостан |
105,6 |
261,3 |
|
Республика Татарстан |
118,5 |
266,8 |
|
Омская область |
102,7 |
272,3 |
|
Томская область |
107 |
273,5 |
|
Красноярский край |
103,2 |
276,9 |
|
Свердловская область |
104,2 |
285,1 |
|
Чукотский авт. округ |
108,2 |
285,8 |
|
Магаданская область |
99 |
290,6 |
|
Камчатский край |
90,8 |
293,2 |
|
Хабаровский край |
83,5 |
294 |
|
Пермский край |
118,9 |
294,5 |
|
Сахалинская область |
113,4 |
372,2 |
|
Тюменская область |
173,3 |
455 |
|
Ямало-Ненецкий авт. округ |
195,9 |
546,1 |
|
Ханты-Мансийский авт. округ-Югра |
221,4 |
547,8 |
2. Полученную упорядоченную
выборку делим на 3 примерно одинаковые
части
.
Тогда 8 первых наблюдений, соответствующих
малым значениям Х (потребление
растительного масла), и 8 последних,
соответствующих большим значениям Х
(потребление растительного масла),
оставляем. А 17 центральных данных удаляем
из рассмотрения.
3. Сформировались две подвыборки:
-
№
У (потребление животное масло)
Х (потребление растительное масло)
Усть-Ордынский Бурятский авт. округ
43,7
82,7
Республика Тыва
41
88
№
У (потребление животное масло)
Х(потребление растительное масло)
Республика Калмыкия
45,5
105,6
Республика Ингушетия
46,3
113
Республика Адыгея
50,8
138,4
Республика Дагестан
50,8
147,5
Республика Марий Эл
64,4
149,4
Чувашская Республика
55,9
149,7
Республика Мордовия
59,5
151,1
Республика Алтай
63,7
154,7
Агинский Бурятский авт. округ
73,2
162,8
Кабардино-Балкарская Республика
65,1
167
Карачаево-Черкесская Республика
66,9
167,2
Забайкальский край
79,9
167,3
Кировская область
53
168,3
Республика Хакасия
66,9
171,8
Удмуртская Республика
68,1
172,7
Еврейская автономная область
65,5
174
№
У (потребление животное масло)
Х(потребление растительное масло)
Краснодарский край
83,1
252,1
Республика Саха (Якутия)
116,6
254,6
Кемеровская область
93,3
258,4
Республика Башкортостан
105,6
261,3
Республика Татарстан
118,5
266,8
Омская область
102,7
272,3
Томская область
107
273,5
Красноярский край
103,2
276,9
Свердловская область
104,2
285,1
Чукотский авт. округ
108,2
285,8
Магаданская область
99
290,6
Камчатский край
90,8
293,2
Хабаровский край
83,5
294
Пермский край
118,9
294,5
Сахалинская область
113,4
372,2
Тюменская область
173,3
455
Ямало-Ненецкий авт. округ
195,9
546,1
№
У (потребление животное масло)
Х (потребление растительное масло)
Ханты-Мансийский авт. округ-Югра
221,4
547,8
4. По известной процедуре МНК строим уравнения линейной парной регрессии для каждой из этих частей.
Получаем для первой части:
,
для последней части:
.
Уже видим, что коэффициенты и а>0>, и а>1> в этих уравнениях заметно отличаются. Это говорит о неоднородности вариации стат. данных, а, значит, о гетероскедастичности.
5. Находим остатки для каждого из этих уравнений, возводим их в квадрат и суммируем:
-
Первая часть выборки
№
Потребление животного масла
Потребление растительное масло
e>i>
e>i>2
Усть-Ордынский Бурятский авт. округ
43,7
82,7
39,061
-4,639
21,521
Республика Тыва
41
88
40,717
-0,283
0,080
Республика Калмыкия
45,5
105,6
46,218
0,718
0,516
Республика Ингушетия
46,3
113
48,531
2,231
4,976
Республика Адыгея
50,8
138,4
56,469
5,669
32,139
Республика Дагестан
50,8
147,5
59,313
8,513
72,475
Республика Марий Эл
64,4
149,4
59,907
-4,493
20,187
Чувашская Республика
55,9
149,7
60,001
4,101
16,817
Республика Мордовия
59,5
151,1
60,438
0,938
0,881
Республика Алтай
63,7
154,7
61,563
-2,137
4,565
Агинский Бурятский авт. округ
73,2
162,8
64,095
-9,105
82,900
Кабардино-Балкарская Республика
65,1
167
65,408
0,308
0,095
Карачаево-Черкесская Республика
66,9
167,2
65,470
-1,430
2,044
Забайкальский край
79,9
167,3
65,501
-14,399
207,319
Кировская область
53
168,3
65,814
12,814
164,198
Республика Хакасия
66,9
171,8
66,908
0,008
0,000
Удмуртская Республика
68,1
172,7
67,189
-0,911
0,830
Еврейская автономная область
65,5
174
67,595
2,095
4,391
Сумма
1060,2
2631,2
1060,2
0,000
635,932
№
Употребление животного масла
потребление растительного масла
e>i>
e>i>2
Краснодарский край
83,1
252,1
92,935
9,835
96,725
Республика Саха (Якутия)
116,6
254,6
93,872
-22,728
516,556
Кемеровская область
93,3
258,4
95,297
1,997
3,987
Республика Башкортостан
105,6
261,3
96,384
-9,216
84,936
Республика Татарстан
118,5
266,8
98,446
-20,054
402,168
Омская область
102,7
272,3
100,508
-2,192
4,806
Томская область
107
273,5
100,958
-6,042
36,510
Красноярский край
103,2
276,9
102,232
-0,968
0,936
Свердловская область
104,2
285,1
105,306
1,106
1,224
Чукотский авт. округ
108,2
285,8
105,569
-2,631
6,923
Магаданская область
99
290,6
107,368
8,368
70,031
Камчатский край
90,8
293,2
108,343
17,543
307,763
Хабаровский край
83,5
294
108,643
25,143
632,174
Пермский край
118,9
294,5
108,831
-10,069
101,394
Сахалинская область
113,4
372,2
137,960
24,560
603,196
Тюменская область
173,3
455
169,002
-4,298
18,477
Ямало-Ненецкий авт. округ
195,9
546,1
203,155
7,255
52,631
Ханты-Мансийский авт. округ-Югра
221,4
547,8
203,792
-17,608
310,040
Сумма
2138,6
5780,2
2138,600
0,000
3250,477
6. Находим отношение большей
суммы квадратов остатков к меньшей, оно
подчиняется F-распределению
Фишера. В данном случае
,
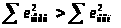поэтому
.
7. Сравниваем его с табличным значением F-критерия Фишера на уровне значимости с (k-1) и (k-1) степенями свободы, где k – объёмы оставшихся частей выборки.
На уровне значимости =0,05
с 17 и 17 степенями свободы табличное
значение
.
8. Выдвигаем гипотезу Н>0> об отсутствии гетероскедастичности (выполнении предпосылки 2). Альтернативная ей Н>1> о наличии гетероскедастичности (нарушении предпосылки 2).
9. Т.к. наблюдаемое значение
превышает табличное:
,
то мы вынуждены принять гипотезу о
наличии гетероскедастичности, подтвердив
свои предположения о нарушении предпосылки
2.
Возможно, этим объясняется большая ошибка аппроксимации.
Т.к. F>e> не намного превышает F>табл>, то можно сказать, что последствия гетероскедастичности выражены несильно, и несильно сказываются на качестве модели. В данном случае эффективнее будет пренебречь этим несильным нарушением предпосылки 2, чем корректировать модель.
Предпосылка 3 О некоррелированности остатков
Т.к. выборка – пространственная, то для таких выборок нарушения этой предпосылки обычно несвойственно, т.к. не участвует фактор времени. Но чтобы убедиться в этом проверим Автокорреляцию остатков хотя бы 1-го уровня.
Полученные остатки сместим на 1 наблюдение – получим остатки 1-го уровня.
-
№
e>i>
e>i-1>
e>i>* e>i-1>
Республика Адыгея
4,5388
Республика Дагестан
7,742
4,5388
35,139
Республика Ингушетия
0,098
7,742
0,759
Кабардино-Балкарская Республика
0,306
0,098
0,030
Республика Калмыкия
-1,7068
0,306
-0,522
Карачаево-Черкесская Республика
-1,4236
-1,7068
2,430
Республика Северная Осетия - Алания
0,4644
-1,4236
-0,661
Краснодарский край
12,2612
0,4644
5,694
Ставропольский край
12,066
12,2612
147,944
Астраханская область
-25,1124
12,066
-303,006
Волгоградская область
0,6932
-25,1124
-17,408
Ростовская область
5,3412
0,6932
3,703
Республика Башкортостан
-7,0004
5,3412
-37,391
Республика Марий Эл
-5,1892
-7,0004
36,326
Республика Мордовия
0,3092
-5,1892
-1,605
Республика Татарстан
-17,9644
0,3092
-5,555
Удмуртская Республика
-0,6876
-17,9644
12,352
Чувашская Республика
3,4164
-0,6876
-2,349
Пермский край
-8,614
3,4164
-29,429
Кировская область
12,8636
-8,614
-110,807
Нижегородская область
6,3964
12,8636
82,281
Оренбургская область
6,0012
6,3964
38,386
Пензенская область
-11,4804
6,0012
-68,896
Самарская область
4,8812
-11,4804
-56,038
Саратовская область
-16,8924
4,8812
-82,455
Ульяновская область
-4,4396
-16,8924
74,995
Курганская область
6,31
-4,4396
-28,014
Свердловская область
2,7772
6,31
17,524
Тюменская область
-6,518
2,7772
-18,102
Ханты-Мансийский авт. округ-Югра
-21,9524
-6,518
143,086
Ямало-Ненецкий авт. округ
2,9492
-21,9524
-64,742
№
e>i>
e>i-1>
e>i>* e>i-1>
Челябинская область
0,8636
2,9492
2,547
Республика Алтай
-2,6236
0,8636
-2,266
Республика Бурятия
-6,5572
-2,6236
17,203
Республика Тыва
-3,402
-6,5572
22,308
Республика Хакасия
0,1956
-3,402
-0,665
Алтайский край
11,6428
0,1956
2,277
Забайкальский край
-14,3884
11,6428
-167,521
Агинский Бурятский авт. округ
-9,2724
-14,3884
133,415
Красноярский край
0,8908
-9,2724
-8,260
Иркутская область
-8,8524
0,8908
-7,886
Усть-Ордынский Бурятский авт. округ
-7,9676
-8,8524
70,532
Кемеровская область
4,2788
-7,9676
-34,092
Новосибирская область
-2,9532
4,2788
-12,636
Омская область
-0,2284
-2,9532
0,675
Томская область
-4,106
-0,2284
0,938
Республика Саха (Якутия)
-20,3588
-4,106
83,593
Камчатский край
19,0284
-20,3588
-387,395
Приморский край
6,0436
19,0284
115,000
Хабаровский край
26,61
6,0436
160,820
Амурская область
15,4124
26,61
410,124
Магаданская область
9,9132
15,4124
152,786
Сахалинская область
24,2364
9,9132
240,260
Еврейская автономная область
2,37
24,2364
57,440
Чукотский авт. округ
-0,9764
2,37
-2,314
-0,9764
Сумма от 2-го по 55-й
-4,3056
1,2099
620,554
Ср. знач.
-0,080
0,022
11,4917331
Станд. откл.
10,36
10,486
Чтобы оценить отсутствие или наличие Автокорреляции 1-го уровня, выясним, есть ли зависимость между остатками модели и остатками 1-го уровня. Из-за смещения останется на 1 значение меньше – 22: со 2-го по 23-е наблюдение. Вычислим коэффициент корреляции между e>i> и e>i>>-1> по его известной формуле:
(где
).
Итак, коэффициент корреляции показывает, что зависимость слабая. Т.е. автокорреляция остатков 1-го уровня слабая. И т.к. выборка пространственная, то этим небольшим нарушением предпосылки 3 можно пренебречь.
Предпосылка 4 О некоррелированности значений фактора и остатков
Построим поле корреляции между фактором Х и остатками е.
По этому расположению точек
делаем вывод о том, ни закономерности,
ни систематического смещения их не
наблюдается.
Рассчитываем коэффициент
корреляции между фактором Х и остатками
е (по
обычной формуле):
.
Значит, фактор Х и остатки е – некоррелированы. Предпосылка 4 не нарушена.
Предпосылки 1 и 5. О нормальном распределении остатков с нулевым матем. ожиданием
По значениям остатков модели построим интервальный вариационный ряд частот. Значения остатков изменяются от min(е)= --25,1124 до max(е)=24,2364. Тогда нижней границей будет -25, а верхней 24, длина всего этого интервала 25+24=49. Его удобно разбить на 7 интервалов. Пусть будет 7 интервалов, их длины 49/7=7. Считаем сколько значений е>i> попадает в каждый из них. И выписываем интервальный вариационный ряд в виде таблицы:
-
Границы
[-25; -18)
[-18; -11)
[-11; -4)
[-4; 3)
[3; 10)
[10; 17)
[17; 24)
Частоты
3
3
11
19
11
5
3
Строим по нему гистограмму частот.
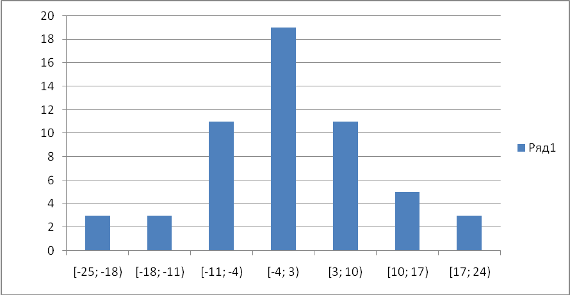
На этом же графике построим график кривой плотности нормального распределения (в соответствующем масштабе) с матем. ожиданием = 0 и сравним форму гистограммы и нормальной кривой.
Для данной выборки можно увидеть, что гистограмма частот остатков более-менее близка по форме к нормальной кривой. Но говорить уверенно о том, что остатки точно распределены нормально, нельзя. Возможно, при большем объёме выборки форма гистограммы была бы более понятной и однозначной.
В данном же исследовании на основании этого графика примем предположение о нормальности остатков. И будем считать, что предпосылки 1 и 5 не нарушены.
Выводы:
Высоко статистически значимые
коэффициенты регрессии а>0>
и а>1>,
коэффициент корреляции
r>ух>
свидетельствуют о наличии сильной
положительной взаимозаменяемости
товаров. Это подтверждается и проверкой
качества уравнения регрессии по
F-критерию
Фишера. Т.е., можно считать, что наличие
взаимозаменяемости статистически
доказано, направление и общая тенденция
отражена уравнением регрессии верно и
согласуется с состоянием рынка
продовольственных товаров. Значения
стандартных ошибок
и
для коэффициентов а>0>
и а>1>
малы, и доверительные интервалы для
параметров модели >0>
и >1>
не широки, а также высокое значение
коэффициента детерминации R2
указывают, что взаимозаменяемость
потребления животного масла растительным
маслом доказана. Влияние же других
экономических (и случайных, в том числе)
факторов – намного менее существенно.
Но средняя ошибка аппроксимации свидетельствует, что в среднем смоделированные данные отличаются от фактических на 9-12%. И в данном исследовании этот уровень можно признать условно приемлемым и только для изученного периода.
В данной модели обнаружена гетероскедастичность остатков. Она обусловлена рыночной ситуацией. Но она несильно нарушает предпосылку 2. Поэтому принято решение, не подвергать модель излишней корректировке, которая вряд ли улучшит её качество.
По результатам проверки остальных предпосылок МНК можно считать, что они выполнены, или, по крайней мере, их негативные последствия минимальны. Для более однозначного ответа требуется увеличение выборки.
Всё это означает, что применение полученного уравнения на другие периоды или другие регионы, и пр. для качественного и реального прогнозирования возможно только с определёнными поправками. И было бы целесообразным для повышения прогностической силы и практической ценности этой модели добавление в нее других факторов, изучение данных и за другие периоды.
Рекомендации по улучшению качества этой модели:
Увеличить выборку для повышения точности.
Добавить в модель и другие факторы (напр., цены на эти продукты, национальные предпочтения, удаленность от производства, сезонные особенности употребления этих продуктов и т. д.), чтобы улучшить аппроксимацию модели.
Внести корректировку для периода времени, чтобы модель была применима не только для изученного периода, ни и для других лет.
Из-за гетероскедастичности можно построить 5 модели: для каждого федерального округа.
1