Анализ временных рядов (работа 1)

РЕФЕРАТ

АНАЛИЗ ВРЕМЕННЫХ РЯДОВ

План

ВВЕДЕНИЕ

ГЛАВА 1. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ

1.1 ВРЕМЕННОЙ РЯД И ЕГО ОСНОВНЫЕ ЭЛЕМЕНТЫ

1.2 АВТОКОРРЕЛЯЦИЯ УРОВНЕЙ ВРЕМЕННОГО РЯДА И ВЫЯВЛЕНИЕ ЕГО СТРУКТУРЫ

1.3 МОДЕЛИРОВАНИЕ ТЕНДЕНЦИИ ВРЕМЕННОГО РЯДА

1.4 МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

1.5 ПРИВЕДЕНИЕ УРАВНЕНИЯ ТРЕНДА К ЛИНЕЙНОМУ ВИДУ

1.6 ОЦЕНКА ПАРАМЕТРОВ УРАВНЕНИЯ РЕГРЕССИИ

1.7 АДДИТИВНАЯ И МУЛЬТИПЛИКАТИВНАЯ МОДЕЛИ ВРЕМЕННОГО РЯДА

1.8 СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ

1.9 ПРИМЕНЕНИЕ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ К СТАЦИОНАРНОМУ ВРЕМЕННОМУ РЯДУ

1.10 АВТОКОРРЕЛЯЦИЯ ОСТАТКОВ. КРИТЕРИЙ ДАРБИНА- УОТСОНА

Введение

Почти в каждой области встречаются явления, которые интересно и важно изучать в их развитии и изменении во времени. В повседневной жизни могут представлять интерес, например, метеорологические условия, цены на тот или иной товар, те или иные характеристики состояния здоровья индивидуума и т. д. Все они изменяются во времени. С течением времени изменяются деловая активность, режим протекания того или иного производственного процесса, глубина сна человека, восприятие телевизионной программы. Совокупность измерений какой-либо одной характеристики подобного рода в течение некоторого периода времени представляют собой временной ряд.

Совокупность существующих методов анализа таких рядов наблюдений называется анализом временных рядов.

Основной чертой, выделяющей анализ временных рядов среди других видов статистического анализа, является существенность порядка, в котором производятся наблюдения. Если во многих задачах наблюдения статистически независимы, то во временных рядах они, как правило, зависимы, и характер этой зависимости может определяться положением наблюдений в последовательности. Природа ряда и структура порождающего ряд процесса могут предопределять порядок образования последовательности.

Цель работы состоит в получении модели для дискретного временного ряда во временной области, обладающей максимальной простотой и минимальным числом параметров и при этом адекватно описывающей наблюдения.

Получение такой модели важно по следующим причинам:

    она может помочь понять природу системы, генерирующей временные ряды;

    управлять процессом, порождающим ряд;

    ее можно использовать для оптимального прогнозирования будущих значений временных рядов;

Временные ряды лучше всего описываются нестационарными моделями, в которых тренды и другие псевдоустойчивые характеристики , возможно меняющиеся во времени , рассматриваются скорее как статистические, а не детерминированные явления. Кроме того, временные ряды, связанные с экономикой , часто обладают заметными сезонными, или периодическими , компонентами; эти компоненты могут меняться во времени и должны описываться циклическими статистическими (возможно, нестационарными) моделями.

Пусть наблюдаемым временным рядом является y>1>, y>2>, . . ., y>n>. Мы будем понимать эту запись следующим образом. Имеется Т чисел, представляющих собой наблюдение некоторой переменной в Т равноотстоящих моментов времени. Эти моменты для удобства пронумерованы целыми числами 1, 2, . . .,Т. Достаточно общей математической (статистической или вероятностной) моделью служит модель вида:

y>t> = f(t) + u>t >, t = 1, 2, . . ., T.

В этой модели наблюдаемый ряд рассматривается как сумма некоторой полностью детерминированной последовательности {f(t)}, которую можно назвать математической составляющей, и случайной последовательности {u>t>}, подчиняющейся некоторому вероятностному закону. ( И иногда для этих двух составляющих используются соответственно термины сигнал и шум). Эти компоненты наблюдаемого ряда ненаблюдаемы; они являются теоретическими величинами. Точный смысл указанного разложения зависит не только от самих данных, но частично и оттого, что понимается под повторением эксперимента, результатом которого являются эти данные. Здесь используется так называемая «частотная» интерпретация. Полагается, что, по крайней мере, принципиально можно повторять всю ситуацию целиком, получая новые совокупности наблюдений. Случайные составляющие , кроме всего прочего, могут включать в себя ошибки наблюдений.

В данной работе рассмотрена модель временного ряда, в которой на тренд накладывается случайная составляющая, образующая случайный стационарный процесс. В такой модели предполагается, что течение времени никак не отражается на случайной составляющей. Точнее говоря, предполагается, что математическое ожидание (то есть среднее значение) случайной составляющей тождественно равно нулю, дисперсия равна некоторой постоянной и что значения u>t> в различные моменты времени некоррелированны. Таким образом, всякая зависимость от времени включается в систематическую составляющую f(t). Последовательность f(t) может зависеть от некоторых неизвестных коэффициентов и от известных величин, меняющихся со временем. В этом случае её называют «функцией регрессии». Методы статистических выводов для коэффициентов функции регрессии оказываются полезными во многих областях статистики. Своеобразие же методов, относящихся именно к временным рядам, состоит в том, что здесь исследуются те модели, в которых упомянутые выше величины, меняющиеся со временем, являются известными функциями t.

Глава 1. Анализ временных рядов

1.1 Временной ряд и его основные элементы

Временной ряд –это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:

    факторы, формирующие тенденцию ряда;

    факторы, формирующие циклические колебания ряда;

    случайные факторы.

При различных сочетаниях в изучаемом процессе или явлении этих факторов зависимость уровней ряда от времени может принимать различные формы. Во-первых, большинство временных рядов экономических показателей имеют тенденцию, характеризующую долговременное совокупное воздействие множества факторов на динамику изучаемого показателя. Очевидно, что эти факторы, взятые в отдельности, могут оказывать разнонаправленное влияние на исследуемый показатель. Однако в совокупности они формируют его возрастающую или убывающую тенденцию.

Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку деятельность ряда отраслей экономики и сельского хозяйства зависит от времени года. При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой временного ряда.

Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой(положительной или отрицательной) случайной компоненты.

В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Основная задача статистического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем чтобы использовать полученную информацию для прогнозирования будущих значений ряда. [5, стр.76]

1.2 Автокорреляция уровней временного ряда и выявление его структуры

При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.

Количественно её можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.

Одна из рабочих формул для расчёта коэффициента автокорреляции имеет вид:

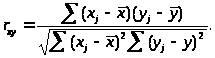(1.2.1)

В качестве переменной х мы рассмотрим ряд y>2>, y>3>, … , y>n>; в качестве переменной у – ряд y>1>, y>2>, . . . ,y>n>> – 1> . Тогда приведённая выше формула примет вид:

(1.2.2)

где

Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями у>t>> >и y>t>> – 1 >и определяется по формуле

(1.2.3)

где

Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Некоторые авторы считают целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило – максимальный лаг должен быть не больше (n/4).

Отметим два важных свойства коэффициента автокорреляции.

Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.

Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержит положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.

Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. Порядков называют автокорреляционной функцией временного ряда. График зависимости её значений от величины лага (порядка коэффициента корреляции) называется коррелограммой.

Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а, следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, то есть при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.

Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка τ, ряд содержит циклические колебания с периодичностью в τ моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической, сезонной компоненты.

1.3 Моделирование тенденции временного ряда

Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда.

Пусть имеются следующие фактические уровни ряда:

у>1>, у>2>, . . ., у>n>>.>

Характер изменения этих уровней, то есть движения динамического ряда, может быть различным. Нашей задачей является нахождение такой простой математической формулы, которая давала бы возможность вычислить теоретические уровни. Основное требование, предъявляемое к этой формуле, состоит в том, что уровни, исчисленные по ней, должны воспроизводить общую тенденцию фактических уровней.

Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:

    линейный тренд: y>t> = a>0> + a>1>t;

    гипербола: y>t> =a>0> + a>1>/t;

    экспоненциальный тренд: y>t> = e a + bt ;

    тренд в форме степенной функции: y>t> = atb;

    парабола второго и более порядков:

y>t >= a>0> + a>1>t + a>2 >t 2 + . . . +a>k >t k .

Аналитическое выравнивание есть не что иное, как удобный способ описания эмпирических данных.

Общие соображения при выборе типа линии, по которой производится аналитическое выравнивание , могут быть сведены к следующим:

    Если абсолютные приросты уровней ряда по своей величине колеблются около постоянной величины, то математической функцией, уравнение которой можно принять за основу аналитического выравнивания, следует считать прямую линию:

y>t> = a>0> + a>1 >t,

где y>t>> >считается как у, выровненный по t.

2) Если приросты приростов уровней, то есть ускорения, колеблются около постоянной величины, то за основу аналитического выравнивания, следует принять параболу второго порядка:

y>t> = a>0 >+ a>1 >t + a>2 >t 2 .

Показатели а>0>, а>1> и а>2> представляют собой в каждом отдельном случае выравнивания постоянные величины, называемые параметрами: а>0 >–начальный уровень; а>1> – начальная скорость ряда и а>2> – ускорение или вторая скорость.

3) Если уровни изменяются с приблизительно постоянным относительным приростом, то выравнивание производится по показательной (экспонентной функции):

y>t> = a>0> a>1>t.

В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путём сравнения коэффициентов автокорреляции первого порядка, рассчитанным по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни y>t> и y >t>> –1 >тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.

При обработке информации на компьютере выбор вида уравнения тенденции обычно осуществляется экспериментальным методом , то есть путём сравнения величины остаточной дисперсии D>ост>, рассчитанной при разных моделях. Имеют место отклонения фактических данных от теоретических (у – у>t>). Величина этих отклонений и лежит в основе расчёта остаточной дисперсии:

(1.3.1)

Чем меньше величина остаточной дисперсии, тем лучше данное уравнение подходит к исходным данным.

1.4 Метод наименьших квадратов

Для нахождения аналитического уравнения, по которому производится выравнивание уровней временного ряда, применяют различные способы. Один из таких способов – метод наименьших квадратов - основан на требовании о том, чтобы сумма квадратов отклонений фактических данных от выровненных была наименьшей:

(у>1 >– у>1>)2 + (у>2> – у>2>)2 + . . . + (у>n> – y>n>)2 = S.

S должно быть наименьшим (минимальным)

Принцип, положенный в основу метода наименьших квадратов, может быть записан в сжатом математическом виде следующим образом:

∑ (y – y>t>)2 = min. (1.4.1)

Из курса математического анализа известно, что при нахождении минимума функции нужно найти частные производные и приравнять их к нулю. Найдём минимум функции, используя уравнение параболы.

Имеем:

∑ (y – y>t> )2 = S; (1.4.2)

заменяем:

y>t> = a>0 >+ a>1 >t + a>2 >t 2

и получаем:

∑( y - a>0 >- a>1 >t - a>2 >t 2 )2 = S.

Находим частные производные функции S сначала по параметру а>0>, а затем по а>1> и а>2>, и приравниваем их к нулю.

;

; (1.4.3)

.

Преобразовывая, получаем:

;

; (1.4.4)

> > .

Полученная система называется системой нормальных уравнений для нахождения параметров а>0> , а>1> и а>2> при выравнивании по параболе второго порядка.

При выравнивании по показательной функции y>t> = a>0> a>1>t параметры а>0> и а>1> определяются по методу наименьших квадратов отклонений логарифмов путём решения системы нормальных уравнений:

; (1.4.5)

.

1.5 Приведение уравнения тренда к линейному виду

Если тренд представляет собой нелинейную функцию, то методы линейного регрессионного анализа для оценки его параметров неприменимы. Но к некоторым нелинейным функциям мы можем применить такие преобразования, которые приведут нас к линейному уравнению.

Если наш тренд представлен степенной линией регрессии, то есть он имеет вид:

y>t> = a>0>ta1, (1.5.1)

то логарифмируя обе части равенства, получим:

ln y>t> = ln a>0> + a>1> ln t.

Отсюда видно, что, введя новые переменные

z = ln y>t> , x = ln t,

мы получим уравнение вида

z = b>0> +a>1>x,

где b>0> = ln a>0>. Это обычное линейное уравнение.

Если линия тренда – парабола второго порядка

y>t> = a>0 >+ a>1 >t + a>2 >t 2 ,

то заменой вида:

х>1> = t, x>2> = t 2,

мы получим линейную функцию двух переменных:

y>t> = a>0 >+ a>1 >х>1> + a>2 >х>2> .

Оценку параметров такой функции можно провести методами линейного регрессионного анализа для множественной регрессии. [5, c.29]

Далее приведём основные понятия регрессионного анализа, которые используются для оценки параметров.

1.6 Оценка параметров уравнения регрессии

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции r>yt>. Существуют разные модификации формулы линейного коэффициента корреляции. Некоторые из них приведены ниже:

, (1.6.1)

или


. (1.6.2)

Как известно, линейный коэффициент корреляции находится в пределах:

-1 ≤ r>yt> ≤ 1.

Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в её линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю ещё не означает отсутствия связи между признаками.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции r>yt>2, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у>t>, объясняемую регрессией, в общей дисперсии результативного признака:

(1.6.3)

где

общая дисперсия результативного признака у;

остаточная дисперсия, определяемая, исходя из уравнения регрессии

у>t> = f(t).

Соответственно величина 1 – r 2 характеризует долю дисперсии у, вызванную влиянием остальных, не учтённых в модели факторов.

Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции R:

(1.6.4)

Иначе, индекс корреляции можно выразить как

Величина данного показателя находится в границах:

0 ≤ R ≤ 1,

чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надёжно найденное уравнение регрессии.

Парабола второго порядка, как и полином более высокого порядка, при лианеризации принимает вид уравнения множественной регрессии. Если же нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого в этом случае совпадёт с индексом корреляции.

Иначе обстоит дело, когда преобразования уравнения в линейную форму связаны с зависимой переменной. В этом случае линейный коэффициент корреляции по преобразованным значениям признаков даёт лишь приближённую оценку тесноты связи и численно не совпадает с индексом корреляции. Так, для степенной функции у>х> = ахb после перехода к логарифмически линейному уравнению lny = lna + blnx может быть найден линейный коэффициент корреляции не для фактических значений переменных х и у, а для их логарифмов, то есть r>lnylnx>. Соответственно квадрат его значения будет характеризовать отношение факторной суммы квадратов отклонений к общей, но не для у, а для его логарифмов:

.

Между тем при расчёте индекса корреляции используются суммы квадратов отклонений признака у, а не их логарифмов. С этой целью определяются теоретические значения результативного признака, то есть , как антилогарифм рассчитанной по уравнению величины и остаточная сумма квадратов как . Индекс корреляции определяется по формуле

В знаменателе расчёта R2>yx> участвует общая сумма квадратов отклонений фактических значений у от их средней величины, а в расчёте r2>lnx>> >>lny> участвует . Соответственно различаются числители и знаменатели рассматриваемых показателей:

- в индексе корреляции и

- в коэффициенте корреляции.

Вследствие близости результатов и простоты расчётов с использованием компьютерных программ для характеристики тесноты связи по нелинейным функциям широко используется линейный коэффициент корреляции.

Несмотря на близость значений R и r или R и r в нелинейных функциях с преобразованием значения признака у, следует помнить, что если при линейной зависимости признаков один и тот же коэффициент корреляции характеризует регрессию, как следует помнить, что если при линейной зависимости признаков один и тот же коэффициент корреляции характеризует регрессию как , так и , так как, то при криволинейной зависимости для функции y=j(x) не равен для регрессии x=f(y).

Поскольку в расчёте индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину для нелинейных связей называют индексом детерминации.

Оценка существенности индекса корреляции проводится, так же как и оценка надёжности коэффициента корреляции.

Индекс корреляции используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:

где - индекс детерминации;

n – число наблюдений;

m – число параметров при переменных х.

Величина m характеризует число степеней свободы для факторной суммы квадратов, а ( n – m - 1) – число степеней свободы для остаточной суммы квадратов.

Для степенной функции m = 1 и формула F – критерия примет тот же вид, что и при линейной зависимости:

Для параболы второй степени y = a>0> + a>1> x + a>2> x2 +εm = 2 и

(1.6.5)

Расчёт F-критерия можно вести и в таблице дисперсионного анализа результатов регрессии, как это было показано для линейной функции.

Индекс детерминации можно сравнивать с коэффициентом детерминации для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации меньше индекса детерминации. Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.

Практически, если величина разности между индексом детерминации и коэффициентом детерминации не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия R2, вычисленных по одним и тем же исходным данным, через t – критерий Стьюдента:

(1.6.6)

m >|>>R>>- >>r>>|> - ошибка разности между R2и r2, определяемая по формуле

Если t> факт> >t> табл> , то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически, если величина t < 2, то различия между R>yx> и r>yx> несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.

1.7 Аддитивная и мультипликативная модели временного ряда

Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания.

Простейший подход- расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда. Общий вид аддитивной модели следующий:

Y= T + S + E.

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой, сезонной и случайной компонент. Общий вид мультипликативной модели выглядит так:

Y = T∙S∙E.

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой, сезонной и случайной компонент. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение аддитивной и мультипликативной моделей сводится к расчету значений трендовой, циклической и случайной компонент для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

    Выравнивание исходного ряда методом скользящей средней.

    Расчет значений сезонной компоненты.

    Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной или мультипликативной модели.

    Аналитическое выравнивание уровней и расчет значений тренда с использованием полученного уравнения тренда.

    Расчет полученных по модели значений или

    Расчет абсолютных и относительных ошибок.

Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.[5, c. 67]

1.8 Стационарные временные ряды

После удаления тенденции (тренда) из временного ряда мы получим стационарный временной ряд. Его можно рассматривать как выборку Т последовательных наблюдений через равные промежутки времени из существенно более продолжительной (генеральной последовательности случайных величин. При этом статистические выводы делаются относительно вероятностной структуры генеральной последовательности. Такую последовательность удобно считать простирающейся неограниченно в будущее и, возможно, в прошлое. Последовательность случайных величин у>1>, у>2>, . . . или . . ., у>-1>, у>0>, у>1>, . . . называется случайным процессом с дискретным параметром времени.

Несмотря на полную произвольность вероятностных моделей последовательностей случайных величин, полезно отличать случайные процессы от множества случайных величин этого процесса, учитывая понятие времени. Грубо говоря, в случайном процессе наблюдения, разделённые небольшими промежутками времени, близки по значениям в отличие от наблюдений, далеко отстоящих друг от друга во времени. Более того, модель значительно упрощается после расширения конечной последовательности наблюдений до бесконечной.

Одним из таких упрощений является свойство стационарности. Будем считать, что поведение множества случайных величин с вероятностной точки зрения не зависит от времени.

Случайный процесс y(t) с непрерывным параметром времени можно определить для 0 ≤ t < ∞ или -∞ < t < ∞ и рассматривать с привлечением вероятностной меры на пространстве функций y(t). Выборка из такого процесса состоит из наблюдений в конечном числе точек времени , или из непрерывных наблюдений в интервале времени.

Наблюдение процесса, часто называемое реализацией, есть точка в соответствующем бесконечномерном пространстве, где определена вероятностная мера. Вероятность определяется на некоторых множествах, называемых измеримыми. Этот класс множеств включает вместе с любым множеством его дополнение, а также объединение и пересечение счётного числа множеств этого класса; вероятностная мера на этом классе множеств определяется таким образом, что вероятность объединения непересекающихся множеств равна сумме вероятностей отдельных множеств.

Практически мы интересуемся вероятностями, которые связаны с конечным числом случайных величин. Эти вероятности включают в себя функцию совместного распределения. [24, c. 88]

1.9 Применение быстрого преобразования Фурье к стационарному временному ряду

Одно из назначений преобразования Фурье- выделять частоты циклических составляющих временного ряда, содержащего случайную компоненту.

Пусть число данных N представимо в виде N = N>1> N>2>. Тогда можно записать

t = t>1> + (t> 2>-1)N>1 >, t>1 >= 1, . . ., N>1> , t>2 >= 1, . . ., N>2> ;

j = j>1> + j> 2>N>2 >, j>1 >= 0, . . ., N>2> – 1 , j>2 >= 0, . . ., N>1> - 1;

Отметим, что a>N>> – >>j> = a>j> и b>N>> – >>j> = - b>j> . Искомые коэффициенты являются соответственно действительной и мнимой частями суммы:

(1.9.1)

Для их отыскания вычислим сначала величины

Для каждой пары ( j>1>, t>1> ) , j>1> = 0, . . ., N>2> – 1 и t>1> = 0, . . ., N>1> . Поскольку

и ,

то существует около N>1>N>2>/2 = N/2 таких пар. После этого находятся действительная и мнимая части суммы (1.9.1):

для j = 0,1, . . ., [N/2]. Число операций умножения приближённо равно N>2>N в первых суммах и 2N>1>N во вторых суммах, так что число операций умножения в целом составляет примерно N (N>2> + 2N>1>). В то же время число произведений в определении коэффициентов a>j> и b>j> , j=0,1, . . ., [N/2] примерно равно N2. [20, c.98], [21, c.78]

1.10 Автокорреляция остатков. Критерий Дарбина- Уотсона

Для каждого момента (периода) времени t = 1 : N значение компоненты >t> для аддитивной модели определяется как

,

где - сумма циклической и трендовой компонент, а для мультипликативной модели:

где - произведение циклической и трендовой компонент.

Ошибки измерений нам неизвестны, а известны лишь эмпирические остатки.

Рассматривая последовательность остатков как временной ряд , можно построить график их зависимости от времени. В соответствии с предпосылками метода наименьших квадратов остатки >t>> >должны> >быть случайными. Однако при моделировании временных рядов часто встречаются ситуация, когда остатки содержат тенденцию или циклические колебания. Это свидетельствует о том, что каждое следующее значение остатков зависит от предшествующих. В этом случае говорят о наличии автокорреляции остатков.

Автокорреляция остатков может быть вызвана следующими причинами, имеющими различную природу. Во-первых, иногда она связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака. Во-вторых, в ряде случаев причину автокорреляции остатков следует искать в формулировке модели. Модель может не включать фактор, существенное воздействие на результат, влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени t. Кроме того, в качестве таких существенных факторов могут выступать лаговые значения переменных, включённых в модель.

Либо модель не учитывает несколько второстепенных факторов, совместное влияние которых на результат существенно в виду совпадения тенденций их изменения или фаз циклических колебаний.

Существует два наиболее распространённых метода определения автокорреляции остатков. Первый метод – это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции. Второй метод – использование критерия Дарбина – Уотсона.

Дж. Дарбин и Г. Уотсон построили таблицы, дающие нижние и верхние пределы порогов значимости. Эти таблицы достаточны для большинства конкретных ситуаций. Рассмотрим логические основания критерия .

Выражение

(1.10.1)

представляет собой «отношение фон Неймана», применённое к остаткам оценки. Этот критерий имеет эффективность аналогичную таковой для критерия r>1>, первого коэффициента автокорреляции остатков. Из предыдущей главы известно, что этот критерий будет особенно мощным, если ошибки следуют авторегрессинному процессу первого порядка. Таким образом, он, по-видимому, хорошо приспособлен для экономических моделей.

Значение d в выборке зависит одновременно от последовательности z>t> и от значений >t>( для t = 1,2, . . . ,N). Однако Дарбин и Уотсон показали, что для заданных значений >t>> >значение d обязательно заключено между двумя границами d> >>U> и d> >>L>> >, не зависящими от значений, принимаемых z>t> , и являющимися функциями лишь чисел N , именно d> >>L>  d  d> >>U>.

Для некоторых значений последовательности z>t> границы d> >>U> и d> >>L>> >могут достигаться. Интервал [d> >>L> ,d> >>U>> >] является, следовательно, наименьшим из возможных, если не принимать во внимание точные значения z>t>.

Границы d> >>U> и d> >>L>> >представляют случайные величины, распределение которых можно определить с помощью точных гипотез относительно распределения >t>.

Для практического использования таблицы полученное значение d* следует сравнить с d>1> и d>2>.

а) Если d* < d>1>, то вероятность столь малого значения наверняка меньше . Гипотеза независимости отбрасывается.

б) Если d* > d>2>, то вероятность столь малого значения наверняка больше . Гипотеза независимости не отбрасывается.

в) Если d> 1>  d*  d> 2 >, то приведённые таблицы оставляют вопрос открытым. Возможно, что гипотезу независимости при уровне значимости  следует отбросить. Однако этого нельзя узнать без изучения закона распределения вероятностей d> >для последовательности переменных z>t> . Практически в этом случае часто довольствуются указанием на то , что значение d* попадает в область неопределённости критерия.

В настоящее время принято приводить значение d* вместе с регрессиями для временных рядов и указывать на расположение этого значения относительно d> 1> и d> 2 .>

Есть несколько существенных ограничений на применение критерия Дарбина – Уотсона.

Во-первых, он неприменим к моделям, включающим в качестве независимых переменных лаговые значения результативного признака, то есть к моделям авторегрессии. Для тестирования на автокорреляцию остатков моделей авторегрессии используется критерий h Дарбина.

Во-вторых, методика расчёта и использования критерия Дарбина - Уотсона направлена только на выявление автокорреляции остатков первого порядка. При проверке остатков на автокорреляцию более высоких порядков следует применять другие методы.

В-третьих, критерий Дарбина – Уотсона даёт достоверные результаты только для больших выборок.