Взаимодействия двух радикально пульсирующих пузырьков газа в жидкости
МИНЕСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ТАТАРСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
Математический факультет
Кафедра вычислительной математики, информатики и методики ее преподавания
КУРСОВАЯ РАБОТА
взаимодействия двух радиально пульсирующих пузырьков газа в жидкости
Выполнил студент 146 группы: Вафин А.А.
Научный руководитель: д. ф. – м. н. Аганин А. А.
Казань – 2007
Содержание
Введение
Постановка задачи в рамках уравнений динамики жидкости
Математическая модель взаимодействия пузырьков
Методика решения
Исследование взаимодействия двух радиально пульсирующих пузырьков газа в жидкости
Заключение
Литература
Приложение. (Программа расчета).
Введение
К настоящему времени довольно хорошо изучена динамика отдельного пузырька газа в жидкости. Полученные в этом отношении результаты имеют важное теоретическое и прикладное значение. Вместе с тем, в реальных жидкостях, как правило, присутствует не один, а множество пузырьков, так что свойства жидкостей существенно зависят от особенностей взаимодействия между пузырьками. В силу большей сложности этот вопрос является менее изученным, хотя он и имеет важное прикладное значение.
В данной курсовой работе исследуется взаимодействия двух радиально пульсирующих пузырьков газа в жидкости ранние выведенной математической модели. В принципе, такое взаимодействие можно изучать и на основе широко известных уравнений Навье-Стокса методом прямого численного моделирования. Однако такой подход пока не используется в силу больших потребностей компьютерного времени даже на современных компьютерах с высоким быстродействием. В модели, использующейся в курсовой работе, жидкость считается невязкой несжимаемой, пузырьки – осесимметричными. Пузырьки расположены сносно. Их общая ось симметрии направлена вертикально вдоль действия силы тяжести. Пузырьки совершают нелинейные радиальные колебания, а скорости их вертикального пространственного перемещения считаются малыми. Используются три системы отсчета, одна неподвижная и две подвижные. В качестве неподвижной системы приняты декартовые координаты, а в качестве подвижных систем – сферические координаты. Начало отсчета радиальных координат в подвижных сферических системах отсчета связано с центрами пузырьков. Поверхности каждого из пузырьков представляются в виде ряда по поверхностным сферическим гармоникам нулевой, второй, третьей, четвертой и т.д. степеней. При этом сферическая гармоника нулевой степени описывает радиальную составляющую поверхности пузырька, а гармоники второй, третьей и т.д. степеней – отклонения от сферической формы в виде соответствующей гармоники (второй степени – эллипсоидальные отклонения, третьей – грушеобразные и т.д.).
Созданная математическая модель представляет собой систему обыкновенных дифференциальных уравнений второго порядка относительно радиусов пузырьков, пространственного положения их центров и амплитуды отклонений от сферической формы пузырьков в виде сферических поверхностных гармоник. При выводе этих уравнений используются частные решения уравнения Лапласа в сферической системе координат и интеграл Коши-Лагранжа.
Постановка задачи в рамках уравнений динамики жидкости
Рассматривается динамика двух газовых пузырьков в неограниченном объеме невязкой несжимаемой жидкости. Динамика жидкости описывается уравнениями
 ,
,
 .
(1)
.
(1)
Здесь
 –
время эйлеровых (неподвижных) систем
координат
–
время эйлеровых (неподвижных) систем
координат
 ,
,
 ,
,
 (нижний индекс
(нижний индекс
 означает частную производную),
означает частную производную),
 –
вектор скорости,
–
вектор скорости,
 –
плотность жидкости,
–
плотность жидкости,
 –
давление,
–
давление,
 ,
,
 ,
,  ,
,  –направляющие
векторы пространственных координат.
Здесь и далее, если не оговорено противное,
по повторяющимся индексам предполагается
суммирование (здесь от 1 до 3).
–направляющие
векторы пространственных координат.
Здесь и далее, если не оговорено противное,
по повторяющимся индексам предполагается
суммирование (здесь от 1 до 3).
П
Рис.1
узырьки расположены вдоль вертикальной оси неподвижной декартовой системы координат
неподвижной декартовой системы координат
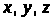 (рис.1).
(рис.1). 
На поверхности каждого пузырька выполняются следующие условия:
кинематическое
 ,
(2)
,
(2)
и динамическое
 .
(3)
.
(3)
Здесь
 –
скорость точки поверхности пузырька,
–
скорость точки поверхности пузырька,
 –
нормаль к поверхности пузырька, верхние
знаки указывают на отношение к внешней
(+) и внутренней (–) сторонам поверхности.
–
нормаль к поверхности пузырька, верхние
знаки указывают на отношение к внешней
(+) и внутренней (–) сторонам поверхности.
Газ в пузырьках принимается гомобарическим (с однородным распределением давления) с давлением, изменяющимся по закону (Ван-дер-Ваальса)
 ,
(4)
,
(4)
где
 –
начальное давление газа в пузырьке,
–
начальное давление газа в пузырьке,
 –
текущий и начальный объемы пузырька,
–
текущий и начальный объемы пузырька,
 –
постоянная,
–
постоянная,
 –
показатель адиабаты.
–
показатель адиабаты.
На бесконечном удалении от
пузырьков давление жидкости
 совершает гармонические колебания
совершает гармонические колебания
 ,
(5)
,
(5)
где
 –
статическое давление в жидкости,
–
статическое давление в жидкости,
 ,
,
 –
амплитуда и частота колебаний.
–
амплитуда и частота колебаний.
Рассматриваются случай, когда форма пузырьков в интересующем промежутке времени остается относительно близкой к сферической.
Математическая модель взаимодействия пузырьков
В пятом приближении относительно
 уравнения динамики двух газовых пузырьков
в вязкой сжимаемой жидкости представляют
собой систему, состоящую из четырех
дифференциальных уравнений относительно
радиусов пузырьков
уравнения динамики двух газовых пузырьков
в вязкой сжимаемой жидкости представляют
собой систему, состоящую из четырех
дифференциальных уравнений относительно
радиусов пузырьков
 ,
координат их центров
,
координат их центров







 ;
;






 ;
;




 ;
;





 ;
;
Методика решения
Имея четыре уравнения второго порядка относительно радиуса и положения центра пузырьков. Вводим замену, чтобы избавится от второго порядка, и запишем уравнения 1 ого порядка:

Получаем систему 8-и уравнений 1-го порядка относительно радиуса, положения центра пузырьков, скорость изменения радиусов и положения центра пузырьков.







 ;
;
 (
(
 )/
)/ ;
;

 /
/ ;
;

 /
/ ;
;

 /
/ ;
;

 /
/ ;
;

 /
/ ;
;








 ;
;
 (
(
 )/
)/ ;
;
 (
( )/
)/ ;
;
 (
( )/
)/ ;
;

 /
/ ;
;

 /
/ ;
;
 (
( )/
)/ ;
;






 ;
;

 /
/ ;
;
 0;
0;
 (
( )/
)/ ;
;
 (
( )/
)/ ;
;

 /
/ ;
;
 (
( )/
)/ ;
;






 ;
;

 /
/ ;
;
 0;
0;
 (
( )/
)/ ;
;
 (
( )/
)/ ;
;

 /
/ ;
;
 (
( )/
)/ ;
;

Отсюда получаем данные уравнения в следующем виде:

Решим уравнение методом последовательных приближений.
В нулевом приближении данные уравнения записываются относительно радиуса и положения центра пузырьков.

Подставляя выражения, находим уравнения нулевого приближения:


В первом приближении уравнения записываются относительно радиуса, положения центра пузырьков, скорость изменения радиусов и положения центра пузырьков. Полученное первое приближение добавляем к нулевому приближению. И так находим до пятого приближения.









Исходя из этого, можем записать следующую систему:

Полученные дифференциальные уравнения решаются методом Дортсмана–Принса восьмой степени точности. (Программа приведена ниже).
Исследование взаимодействия двух радиально пульсирующих пузырьков газа в жидкости
Для учета влияния вязкости и сжимаемости жидкости проводим следующую модификацию математической модели. (По аналогии с работой Дойникова[?]).
С учетом сжимаемости жидкости получим следующие уравнения:










 ;
;





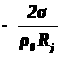




 ;
;
Решение для нулевого приближения для одного пузырька





 ;
;
Вводим замены:
 ;
;
 ;
;
 ;;
;;
 =
= =
= ;
;
 - начальное давление газа в
пузырьке;
- начальное давление газа в
пузырьке;
 ;
-давление газа в пузырьке.
;
-давление газа в пузырьке.


А - константа Ван-дер-Ваальса;
 -
коэффициент поверхностного натяжения;
-
коэффициент поверхностного натяжения;
 - давление газа в пузырьке;
- давление газа в пузырьке;
 - статическое давление в
жидкости;
- статическое давление в
жидкости;
 -
Начальный радиус пузырька;
-
Начальный радиус пузырька;
R - Радиус пузырька;
 - Центр пузырька;
- Центр пузырька;
u - Вектор скорости жидкости;
 -давление
в жидкости на большом удалении от
пузырька, где
-давление
в жидкости на большом удалении от
пузырька, где
 -
амплитуда и частота колебаний давления.
Рассматривается лишь один период
колебаний (
-
амплитуда и частота колебаний давления.
Рассматривается лишь один период
колебаний ( ).
).

 -
Плотность жидкости;
-
Плотность жидкости;
 -
Скорость звука в жидкости;
-
Скорость звука в жидкости;
 -
Кинематический коэффициент вязкости
-
Кинематический коэффициент вязкости
 - расстояние между пузырьками.
- расстояние между пузырьками.





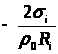 ;
;






 ;
;
Обозначим слагаемые и сомножители
через:
 ,
,
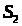 ,
, ,
, ,
, :
:

 ;
;

 ;
;

 ;
;


 ;
;

 ;
;




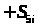
 ;
;


 ;
;
Добавляем второе уравнение:

 =0
=>
=0
=>

 ;
;

 ;
;
Добавляем уравнение второго пузырька





 ;
;
 ;
;
 ;
;
 ;
;
 =
= =
= ;
;





 ;
;






 ;
;

 ;
;

 ;
;

 ;
;


 ;
;

 ;
;





 ;
;


 ;
;
Добавляем второе уравнение:

 =0
=>
=0
=>

 ;
;

 ;
;
Решение для первого приближения одного пузырька

 ;
;
 ;
;








 ;
;





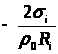 ;
;

 (
(



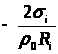
 );
);
 ;
;


Добавляем уравнение второго пузырька

 ;
;
 ;
;








 ;
;







 ;
;
 ;
;


Решение для второго приближения одного пузырька


 ;
;


 /
/

 ;
;

 ;
;

 (
(



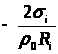

 );
);
 ;
;

 ;
;
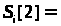

Добавляем уравнение второго пузырька


 ;
;





 ;
;

 ;
;







 ;
;








 ;
;
 ;
;



Решение для третьего приближения одного пузырька



 ;
;



 )/
)/

 ;
;

 ;
;

 ;
;






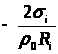


 ;
;
 ;
;

 ;
;

 ;
;


Добавляем уравнение второго пузырька



 ;
;






 ;
;



 ;
;








 ;
;








 ;
;
 ;
;
 ;
;
 ;
;


Решение для четвертого приближения одного пузырька




 ;
;




 )/
)/

 ;
;

 ;
;

 ;
;

 ;
;






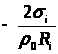



 ;
;
 ;
;

 ;
;

 ;
;

 ;
;


Добавляем уравнение второго пузырька




 ;
;







 ;
;

 ;
;

 ;
;

 ;
;









 ;
;










 ;
;
 ;
;
 ;
;
 ;
;




Решение для пятого приближения одного пузырька





 ;
;





 )/
)/

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;






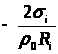




 ;
;
 ;
;

 ;
;

 ;
;

 ;
;

 ;
;


Добавляем уравнение второго пузырька





 ;
;








 ;
;

 ;
;

 ;
;



 ;
;










 ;
;










 ;
;
 ;
;
 ;
;
 ;
;






Для исследования добавляем вязкость и решаем уравнение:






 ;
;






 ;
;
где
 ,
(j
= 1, i
= 2);
,
(j
= 1, i
= 2);
 - Кинематический коэффициент
вязкости;
- Кинематический коэффициент
вязкости;
 ,
,
 ,
,
 ,
,
 ,
,

Вводим замену, чтобы избавится от второго порядка, и запишем уравнения 1 ого порядка:




Для первого уравнения:
 ;
;

 =
= ;
;






 ;
;





 ;
;

 ;
;
 0;
0;

 ;
;

 ;
;

 ;
;

 ;
;
Для второго уравнения:
 ;
;

 =
= ;
;






 ;
;





 ;
;

 ;
;
 0;
0;

 ;
;

 ;
;

 ;
;

 ;
;

|
Рис.1. Изменение радиуса пузырька и положения его центра во времени. |