Імітаційна модель взаємодії підприємства з ринком

ВСТУП

На сучасному етапі Українська держава здійснює перехід до ринкової системи господарювання, в зв’язку з чим постає дуже актуальним питання технологій діяльності підприємства на ринку. Повільність та негаразди пов’язані з цим процесом можна пояснити тим, що більшість підприємців та полісі-мейкерів (особи, що приймають політичні рішення) не усвідомлюють того, що кожний суб’єкт ринку взаємопов’язаний з будь-яким іншим, а отже має вплив фактично на всю ринкову систему. Протиріччя, що виникають внаслідок неврахування цього факта й спричиняють наявну важкість ринкових реформ в державі. Ці протиріччя не дають нормально спрацьовувати об’єктивним ринковим законам, а отже більшість підприємців намагаються якомога швидше отримати якнайбільший прибуток і зберегти за рахунок швидкості мобільність капіталу.

Якщо абстрагуватися від українських реалій, стає очевидним, що на сучасному етапі розвитку світової спільноти успішна діяльність в будь-якій галузі міжлюдських відносин залежить від глобальності сприйняття цієї галузі. Кожна така галузь є системою, що складається не тільки з великих структурних одиниць, які суттєво впливають на процеси, що відбуваються в системі, але й з великої кількості дрібних учасників. Неприйняття до уваги цих дрібних учасників може призвести до фатальних помилок в визначенні тенденцій подальшого розвитку системи. Наслідки таких помилок можуть бути дуже різними. Якщо взяти конкретно економічні системи, це може бути, як збанкрутування невеличкого підприємства, так і розпад економіки країни внаслідок помилок на рівні державних рішень або потужних фінансових інститутів.

Які б не були думки з цього приводу, дуже велику роль в економічних системах відіграють закони ринку, зокрема їх математичне вираження. Ось тут на допомогу фінансисту, маркетологу або спреціалісту в іншій галузі економічних знань прийде на допомогу потужний аппарат сучасної математичної науки. Тобто, якщо є залежності, які можливо виразити математично, досить нескладно оцінити стан та процеси, що відбуваються в системі, а також спрогнозувати її подальший розвиток.

Таким чином, завданням моделі, що ми її будемо будувати є оцінка наявної ситуації та впливу чинників ринку на розвиток системи або її суб’єкта і таким чином визначити тенденції розвитку системи за конкретних значень параметрів ринку. Модель побудована в суворій відповідності із економічними законами, для того щоб якомога точніше прогнозувати процес розвитку існуючої системи з конкретними параметрами. Параметрами нашої моделі будуть лише основні чинники, що впливають на діяльність підприємства та обсяг її пропозиції :

• місткість ринку ;

• дефіцит ринку ;

• ціна рівноваги ;

• постійні та змінні витрати ;

• тривалість виробничого цикла підприємства ;

• початковий обсяг пропозиції .

Тут треба зазначити, що, взагалі кажучи, жодна модель, скільки б факторів ринку вона не враховувала, не здатна кількісно передбачити наслідки змін в системі. Тобто застосування математичних моделей є панацеєю від усіх неприємностей та несподіванок, які так часто трапляються на ринку.

Але, безумовно, позитивною стороною моделей є зниження ризиків в діяльності підприємства майже до рівня форс-мажорних обставин, тобто вони дозволяють отримати точні та однозначні тенденції розвитку. Отже побудова і використання моделей в роботі підприємства є дуже важливою складовою управлінського процесу на ньому.

Повертаючись до ситуації в Україні зазначимо, що необхідним на даний час є створення і формування громадської думки щодо використання математичних моделей в економіці, особливо на рівні потужних фінансових інститутів та стратегічних державних рішень, які стосуються розвитку ринкових відносин. За таких умов можуть бути зроблені важливі й виважені кроки з реформування економіки до довгоочікуваної стабілізації та економічного зростання.

Звичайно, побудована модель є досить простою і не відповідатиме вимогам ринку. Проте за її допомогою вже можна отримати дуже цікаві закономірності розвитку підприємств на ринках від чистої конкуренції до чистої монополії.

Ця модель може бути використана в процесі вивчення економічних дисциплін, як ділова гра. Також вона відкрита для доопрацювання і вдосконалення і створення на її базі більш детальної і потужної моделі.

1. Опис моделі.

В

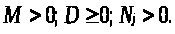
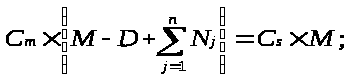
основі побудови даної моделі лежить припущення, що стосується загального обсягу реалізації продукту на ринку, як-то : поточний обсяг реалізації продукції дорівнює обсягу реалізації за умови, що ринок знаходиться в стані економічної рівноваги (економічна рівновага характеризується збалансованістю попиту і пропозиції усіх ресурсів системи):

Д

е :

М, [ одиниця / час] - місткість ринку, тобто обсяг товарної маси, що може бути реалізований на конкретному товарному ринку ( ринку даного продукту) за певний проміжок часу за певних умов ( рівні цін, насиченості ринку і т. п.);

D, [ одиниця / час] - дефіцит ринку - недостача продукції і послуг, викликана недостатнім обсягом їх виробництва або невиправданим складом ( асортиментом) випуску або необгрунтованістю співвідношень у структурі цін і прибутків;

N, одиниця / час - пропозиція j-го суб'єкта ринку;

n - кількість пропозицій;

См, [грн./ одиниця] - поточна ринкова ціна;

Cs, [грн. / одиниця] - рівноважна ринкова ціна.

Природньо, у даному випадку важливим є тільки характер даного припущення - зниження поточної ринкової ціни при збільшенні пропозиції і навпаки. Таку тенденцію будемо описувати ціновим коефіцієнтом ринку С. З (1.1) випливає :

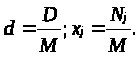
Очевидно, що перша похідна ( r = 1 ) завжди від'ємна, тобто, як уже було сказано, при збільшенні пропозиції ціна буде падати. Крім того, у випадку, коли ринок знаходиться в стані рівноваги, тобто товарний дефіцит дорівнює сукупній ринковій пропозиції, ціновий коефіцієнт C буде дорівнювати 1 ( С = 1), тобто на ринку встановлюється ціна рівноваги. У випадку, коли пропозиція перевищує товарний дефіцит, ціна починає падати і при необмеженому зростанні пропозиції прямує до нуля. Якщо ж попит перевищує пропозицію на величину товарного дефіциту, то ціновий коефіцієнт C стає більше 1 ( С>1 ), і з ростом дефіциту ціна збільшується, що створює сприятливу економічну кон'юнктуру для виробників споживчих товарів. Графік цінового коефіцієнта C показаний на малюнку 1.1 : а) d=0; =0;

б) d=0; =0,5;

в) d=0,25; =0;

г) d=0,25; =0,5,

де

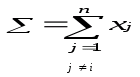
сумарна ринкова пропозиція без урахування пропозиції i-гo суб'єкта ринку.

Для побудови даної моделі необхідно також ввести поняття собівартості продукції - грошовий вираз витрат на виробництво і реалізацію продукції. Собівартість, як відомо, безпосередньо впливає на кінцеві економічні результати господарювання, в її основі лежать витрати виробництва. Витрати будь-якого підприємства за певний період часу дорівнюють вартості ресурсів, що було витрачено на виробництво певної кількості продукції чи послуг. Існують два підходи до визначення витрат: бухгалтерський та економічний. Бухгалтерський враховує тільки ті, що мають форму грошових платежів. Економічне розуміння витрат базується на обмеженості ресурсів і можливості їх альтернативного використання.

Економічні витрати дорівнюють сумі нормального прибутку, явних ( бухгалтерських) та неявних витрат. Неявні витрати можуть бути представлені як грошові платежі, які підприємство може отримати при більш ефективному використанні ресурсів. Нормальний прибуток - це мінімальна винагорода, яку підприємство повинно отримати за розвиток даного виду бізнесу. Наведемо деякі класифікації витрат, а саме:

1. За місцем у системі керування:
а) виробничі витрати;
б) невиробничі витрати ( загальні витрати фірми).

2. Ступеня їхньої відслідкованості:
а) прямі витрати;
б) непрямі витрати.

3.Часу їх дебетування відносно надходжень від реалізацій:

а) витрати, що входять у виробничу собівартість;

б) витрати періоду.

4.Динаміки їхніх функціональних змін:
а) змінні витрати;
б) постійні витрати.

5.Ступеня їх усереднення:
а) повні витрати;
б) витрати, що входять в питому собівартість.

6. Їхньої значимості для планування:
а) регульовані і нерегульовані витрати;
б) нормативні витрати;
в) прирістні витрати;
г) витрати минулого періоду;
д) наявні виплати;
е) значимі витрати ( майбутнього періоду);
ж) витрати, що входять до альтернативної вартості.

Проте, із погляду рівноважного аналізу для нас важливі тільки постійні і змінні витрати, оскільки рівноважний аналіз є об'єктом ряду припущень, що обмежують, як-от:

1. Усі витрати повинні підрозділятися на змінні і постійні;

2. Величина змінних витрат на одиницю продукції повинна залишатися постійною;

3. Повинен бути один вид продукту й одна структура продажу;

4. Обсяг виробництва повинен залишатися єдиним чинником, що впливає на величину перемінних витрат.

Отже, ми будемо розглядати витрати тільки як змінні, пов'язані з ростом обсягу продукції, що виробляється, і постійні, що характеризують ефективність керування і не пов'язані з ростом обсягу продукції.

У змінні витрати входять усі прямі матеріальні витрати (сировина, матеріали, паливо й електроенергія на технологічні цілі і т. п. ) і трудові витрати ( оплата праці робочих із відрахуваннями на соціальні потреби ).

До постійних витрат відносяться: амортизація виробничого устаткування, оплата праці управлінського складу, витрати на утримання помешкань і технічне обслуговування устаткування, витрати на маркетингові дослідження і рекламу, придбання нових технологій і т п.. п.

Отже, для побудови даної моделі будемо розглядати витрати тільки як постійні і змінні.

Виходячи з цього, можна записати формулу собівартості на одиницю продукції:

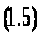
Тут Ai - змінні витрати на одиницю продукції i-го суб'єкта ринку;

Bi - постійні витрати i-го суб'єкта ринку;

Ni - поточний обсяг випуску продукції i-го суб'єкта ринку.

А

оскільки має місце (1.2):

Тоді вираз (4) можна переписати у вигляді:

У ході подальшої побудови моделі доцільніше розглядати приведену величину функції собівартості i-го суб'єкта ринку, тому що раніше отриманий вид даної функції не дозволяє порівнювати її із ціновим коефіцієнтом, що необхідно для аналізу прибутку, оскільки ми одержали несумірні величини. Будемо розглядати відношення:

З (1.2) і (1.6) одержимо:

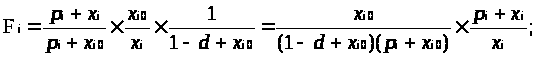
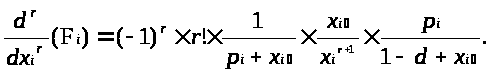
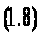
Тут :

x_>I0> > 0 - постійна величина, що позначає мінімальний стартовий рівень пропозиції при n=1 ( за умови відсутності конкурентів), іншими словами, це такий обсяг випуску продукції, при якому підприємство почне отримувати прибуток від своєї діяльності. Таким чином, величина обсяга виробленої продукції в початковий момент часу не повинна бути менше x_>I0>, оскільки в іншому випадку це буде збитково для підприємства. Значення x_>I0> безпосередньо залежить від величини витрат підприємства. І незважаючи на те, що цей параметр визначений як "вхідний" у даній моделі, його можна визначити, знаючи ситуацію, що склалася на ринку (місткість ринку, його дефіцит і сукупна пропозиція) і функцію собівартості підприємства, тобто С і F_>i>. .

p_>I>_> > - параметр конкурентноздатності i-го суб'єкта ринку, він характеризується величиною відношення постійного капіталу до змінного:

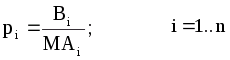
Знак першої похідної (1.8) від'ємний, що означає зниження собівартості при збільшенні величини пропозиції і навпаки. Графік Fi показаний на малюнку 1.2:

а) d = 0,2; x_>I0> = 0,1; p_>I> = 0,06;

б) d = 0,2; x_>I0> = 0,1; p_>I> = 0,08;

в) d = 0,2; x_>I0> = 0,2 p_>I> = 0,5.

На малюнку 1.3 зображений конкретний приклад розташування кривих С і Fi. Крива С : а) d = 0,2; Σ = 0,06. Крива Fi: б) d = 0,2; x_>I0 >= 0,1; p_>I> = 0,06. Графіки С і Fi мають дві точки перетину x_>I0> і x_>IF>. У діапазоні x_>I0> < x_>I>_> >< x_>IF> величина ( C-Fi ) буде додатньою. Це означає, що в даному діапазоні значень x_>I> собівартість i-гo суб'єкта ринку буде менше ринкової ціни, тобто здійснюючи випуск продукції у вищевказаних межах підприємство буде отримувати прибуток, виробляючи ж продукцію на рівні x_>I0> або x_>IF> - підприємство буде лише покривати свої витрати, ну а в усіх інших випадках воно буде зазнавати збитків.

Для того, щоб визначити, як же співвідносяться між собою точки x_>I>_>0> і x_>IF>, прирівняємо праві частини співвідношень (1.2) і (1.7):

Вирішуючи рівняння (1.10) при n=1, одержимо наступне:

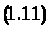
У деяких окремих випадках Fi має такі значення:

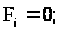
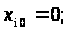
Отже, ми нарешті впритул підійшли до того, щоб ввести основне рівняння, що імітує динаміку виробництва групи підприємств, що функціонують на ринку, і що дозволяє продемонструвати як деякі ефекти конкурентної боротьби, так і ряд можливостей керування нею:

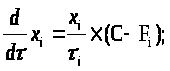
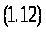
Тут: [ час ] - поточний час;

 _>i> [ час ] - тривалість виробничого циклу.

Дане рівняння дозволяє зробити наступне припущення: швидкість зміни пропозиції пропорційна швидкості зміни прибутку. Дійсно, вираз ( С - Fi ) позначає прибуток ( збиток ) підприємства. У випадку, коли ця величина додатня ( підприємство отримує прибуток в даний момент часу ), похідна x_>I> буде також додатньою, що означає успіх підприємства на ринку, тобто збільшення обсягів виробництва підприємства в наступному виробничому циклі. В іншому випадку ( підприємство зазнає збитків) похідна буде від'ємною, а отже темпи виробництва будуть поступово знижуватися, що згодом при відсутності заходів з боку підприємства ( або держави), спрямованих на його вихід із критичного становища, може привести до банкрутства.

Крім того, варто відмітити, що права частина рівняння (1.12) складається з двох множників. Перший відповідає додатньому зворотному зв'язку суб'єкта ринку на самого себе, тобто створює його експоненціальне зростання. Другий обмежує це зростання. З урахуванням (1.2), (1.7), (1.12) систему диференціальних рівнянь динаміки ринку можна записати в такий спосіб:

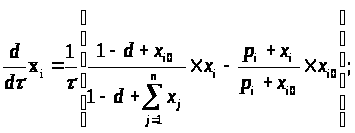
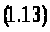
Систему диференціальних рівнянь (1.13) можна записати й у дискретному вигляді:

k = 0, 1, 2,...- дискретний час.

Такий запис дозволяє запрограмувати дану систему для зручностей аналізу.

Запропонована система диференціальних рівнянь (1.13), незважаючи на граничну простоту, демонструє основні принципи функціонування економічних систем і керування ними, виявляє і дозволяє аналізувати такі явища як банкрутство, залежність динаміки виробництва від податкової політики держави і ряду інших чинників, демонструє можливості економічних методів керування виробництвом, дозволяє планувати й оцінювати їхню стратегію.

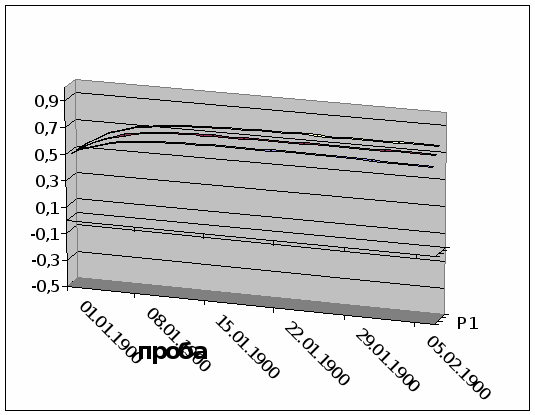
Графік системи рівнянь (1.13) приведений на малюнку 1.4 :

n = 5; d = 0,4:

а) x_>i0> = 0,01; p_>i> = 0,0l; х_>i>(t0) = 0,5;  = 1;

б) x_>i0> = 0,065; p_>i> = 0,008; х_>i>(t0) = 0,4;  = 0,8;

в) x_>i0> = 0,0065; p_>i> = 0,0l5; х_>i>(t0) = 0,1;  = 1;

г) x_>i0> = 0,005; p_>i> = 0,0l5; х_>i>(t0) = 0,065;  = 0,7;

д) x_>i0> = 0,01; p_>i> = 0,025; х_>i>(t0) = 0,25;  = 1.

2. Аналіз впливу параметрів системи x_>i>_>0 >, x_>i> (_>0> ), d на обсяг пропозиції x_>i> і-го суб'єкта ринку.

Як уже було показано на малюнку 1.4 еволюція системи (1.13), при повній відсутності керування або в результаті некомпетентного керування приходить до монополізму (n = 1). У розглянутій системі з n підприємств відбувається конкурентна боротьба. У результаті виживає тільки одине, усі інші стають неплатоспроможними. Від чого ж залежить успіх того або іншого підприємства? Спробуємо з'ясувати це шляхом аналізу розглядаємої моделі, а точніше проаналізувавши динаміку змін параметрів x_>i>_>0 >, x_>i> (_>0> ), d. Для спрощення аналізу простежимо динаміку зміни вищевказаних параметрів на прикладі одного підприємства, тобто перевіримо як буде змінюватися рівень пропозиції підприємства в залежності від зміни того або іншого параметра при фіксованих інших.

Дуже важливу роль відіграє параметр x_>i>_>0>. Ця величина разом з величиною х_>if>_> > визначає ліву та праву границі інтервалу беззбитковості виробництва для того чи іншого суб’єкта ринку (при умові відсутності конкурентів). Цей результат було отримано в першій частині даної роботи, однак не було сказано жодного слова про те, що в залежності від параметра конкурентоспроможності р точка x_>i>_>0> може визначати праву або ліву границі. Взагалі кажучи, це очевидно випливає з виразу (1.11). Подивимось, коли ж саме параметр x_>i>_>0> визначає праву границю, а коли ліву. З формули (1.11) випливає, що існує таке р*:

що як тільки р < р*  x_>i>_>0 >< x_>if>_> >(x_>i>_>0 >визначає праву границю інтервалу беззбитковості);
як тільки р < p*  x_>i>_>0 > > x_>if>_> > (x_>i>_>0 > визначає ліву границю інтервалу беззбитковості).

Оскільки величини x_>i>_>0 > та x_>if> визначають інтервал беззбитковості, то цілком очевидним є той факт, що якщо підприємство буде працювати за межами цього інтервалу, то воно збанкрутує.

Однак повернемось до аналізу параметру х_>i>_>0> та інтервалу [ x_>i>_>0>; x_>if>]. Очевидно, що, чим ширше цей інтервал, тим нижче розташована крива собівартості по відношенню до кривої цінового коефіцієнту на графику, тим більший прибуток отримує підприємство. Крім того, маленька величина x_>io> означає, що підприємство може стартувати навіть при дуже невеликому початковому капіталі і при цьому не терпітиме збитків. В якості прикладу можна навести ринок дефіцитних товарів. Величина d на такому ринку досить велика, що є причиною дуже високих цін, в той час як витрати на виробництво цих товарів в середньому можуть бути невеликими. Подібний приклад не може свідчити про ефективність ведення діяльності, він говорить лише про інтуіцію власника даного підприємства, який вчасно і вдало вклав гроші, іншими словами “влучив”. Однак, тривалий час така ситуація не зберігатиметься. "Прибутковість" ринку приверне увагу багатьох підприємств, і товар перестане бути дефіцитним. І в такому випадку уціліють лише ті підприємства, які через ефективне керування та використання ресурсів, зможуть реально знизити собівартість своєї продукції. Ну, а якщо величина x_>i>_>0> = 0, то яким би не був рівень виробництва ( звичайно, він повинен бути відмінним від нуля, инакше це означає, що підприємство взагалі не веде ринкової діяльності ), підприємство завжди буде отримувати прибуток. Підводячи підсумок, можна відмітити, що між величиною товарної пропозиції підприємства та параметром х_>i>_>0> простежується зворотній зв’язок: чим менший мінімальний стартовий рівень пропозиції х_>i>_>0> може собі дозволити підприємство при інших фіксованих умовах, тим краще воно функціонує, тим більший обсяг випуску продукції х_>i> воно може проводити. Подібна ситуація представлена на малюнку 2.1:

а) d = 0,2 ; p_>i>_> >= 0,015 ; _>i> = 1 ; х_>i>_>0> = 0,01 ; х_>i>_>0>(_>0>) = 0,4;

б) d = 0,2 ; p_>i> = 0,015 ; _>і> = 1 ; х_>i>_>0 > = 0,025 ; х_>i>_>0>(_>0>) = 0,4;

в) d = 0,2 ; p_>і> = 0,015 ; _>і> =1; х_>i>_>0> = 0,05 ; х_>i>_>0 >(_>0>) = 0,4;

г) d = 0,2 ; p_>i> = 0,015 ; _>i>= 1; х_>i>_>0 >= 0,012 ; х_>i>_>0>(_>0>) = 0,4;

д) d = 0,2 ; p_>і> = 0,015 ; _>і> =1; х_>i>_>0> = 0,015 ; х_>i>_>0 >(_>0>) = 0,4.

Розглянемо вплив зміни тривалості виробничого цикла  (при фіксованих інших параметрах) на обсяг пропозиції і-го суб’єкта ринку х_>i>. Чим коротше виробничий цикл товара, тим скоріше будуть обертатися вкладені у виробництво кошти. Так, якщо підприємству вдається скоротити свій виробничий цикл ( при незмінних інших показниках господарської діяльності ), то його прибуток збільшиться. А оскільки дана модель побудована, виходячи з припущення про те, що швидкість зміни пропозиції пропорційна швидкості зміни прибутку, то логічно зробити такий висновок : чим менше тривалість виробничого цикла підприємства, тим більше обсяг виробництва продукції. Іншими словами, хто швидше крутиться, той “крутіше”. Дана ситуація илюструється малюнком 2.2:

а) d = 0,2 ; p_>i>_> >= 0,015 ; _>i> = 1 ; х_>i>_>0> = 0,001 ; х_>i>_>0>(_>0>) = 0,4;

б) d = 0,2 ; p_>i> = 0,015 ; _>і> = 0,9 ; х_>i>_>0 > = 0,001; х_>i>_>0>(_>0>) = 0,4;

в) d = 0,2 ; p_>і> = 0,015 ; _>і> =0,8; х_>i>_>0> = 0,001; х_>i>_>0 >(_>0>) = 0,4;

г) d = 0,2 ; p_>i> = 0,015 ; _>i>= 0,7; х_>i>_>0 >= 0,001; х_>i>_>0>(_>0>) = 0,4;

д) d = 0,2 ; p_>і> = 0,015 ; _>і> =0,5; х_>i>_>0> = 0,001 ; х_>i>_>0 >(_>0>) = 0,4.

В завершенні аналізу впливу параметрів системи на обсяг пропозиції необхідно також сказати про дефіцит ринку d. З ростом дефіциту на той чи інший товар, ціна на нього також буде змінюватися в сторону збільшення. Це означає, що прибуток, який отримує підприємство, буде збільшуватись. Отже, чим більший дефіцит на ринку, тим краще на ньому працювати підприємству.

3. Знаходження оптимального обсягу випуску продукції.

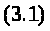
Як було встановлено раніше точки перетину графіків цінового коефіціенту та витрат співвідносяться наступним чином :

Беззбитково працювати підприємство може лише в області обмеженій точками перетину х_>i0 ><х_>i> <х_>i>_>f>_> >. При інших значеннях х_>i> діяльність підприємства буде збитковою через перевищення витрат над ціною. Важливим показником для підприємства є обсяг випуску при якому буде досягатися максимальний прибуток. Для знаходження оптимального обсягу виробництва (пропозиції) розглянемо добуток обсягу виробництва х_>i> на різницю між ціною та собівартістю:

З точки зору графічної інтерпритації це означає, що необхідно знайти прямокутник, одна сторона якого буде дорівнювати величині віпуску продукції x_>i>, а друга - різниці між ринковою ціною та собівартістю, тобто прибутку на одиницю продукції при такому обсязі виробництва, при цьому площа прямокутника повинна бути максимальною.

Знайдемо похідну цього виразу та прирівняємо її до нуля. Звідси отримаємо вираз для оптимального значення обсягу виробництва (пропозиції) і-го підприємства:

Цей вираз визначає такий об’єм пропозиції (виробництва) і-того підприємства, при якому величина прибутку цього підприємства буде максимальною. Але підприємству не завжди доцільно намагатися максимізувати прибутки в конкретний момент часу, тому що притримуючись такої стратегії можна втратити частину ринку. Така стратегія може бути застосована у випадку, коли підприємство зацікавлене в отриманні максимального прибутку в короткий термін з подальшим виходом з ринку. Наприклад, компанії терміново потрібні значні фінансові ресурси для покращення свого становища на основному ринку (підриву позицій конкурентів). Для цього вона може інвестувати кошти в інший бізнес, вклавши основну частину в оборотний капітал – закупівля сировини та матеріалів. При цьому звівши до мінімуму капітальні вкладення – придбавши не найкраще, а можливо й не нове обладнання. Це дасть змогу при необхідності вийти з ринку з найменшими втратами і швидко. Вираз “при необхідності” використано не випадково, оскільки обставини можуть скластися таким чином, що новий ринок буде більш привабливим і компанія взагалі переорієнтує свою діяльність.

З іншого боку, коли метою підприємства є тривале знаходження на даному ринку, така стратегія є недоцільною. В таких випадках компанії скоріше прийдеться відмовитися від ідеї швидко “відбити” вкладені кошти на користь зміцнення своїх позицій та збільшення долі ринку. Адже пануваня на ринку варте того, щоб трохи зачекати.

4. Кількість підприємств на ринку.

Розглянемо параметр конкурентноздатності підприємства р. Цей параметр характеризується структурою витрат підприємства. Під структурою витрат розуміється процентне співвідношення постійних і змінних витрат. Так, якщо валові витрати виробничих підприємств “А” і “В” співвідносяться в такий спосіб:

	підприємство “А”	підприємство “В”
Постійні витрати	35%	60%
Змінні витрати	65%	40%
Валові витрати	100%	100%

то можна зробити висновок, що ці підприємства мають різну структуру витрат.

Типовою причиною такої різниці може бути те, що підприємство “А” має менший ступінь автоматизації і, отже, великою потребою у використанні ручної праці. Постійні витрати фірми “А” на амортизацію виплату відсотків на капітал, використаний на придбання устаткування, та інше в зв'язку з цим будуть достатньо невеликі, у той час як змінні витрати на оплату праці, навпаки, значними. З підприємством “В” справа полягає протилежною образом: значна частка постійних витрат у складі валових може свідчити про високий ступінь автоматизації, гарній підготовці кадрів, у тому числі й управлінського персоналу, і відповідно про незначні змінні витрати на оплату ручної праці. Очевидно, що підприємство “В” у даному випадку є більш конкурентоспроможним, ніж підприємство “А”. Подібна ситуація і характеризується його великим параметром конкурентноздатності р (при фіксованих інших параметрах).

Крім того, можна відзначити, що існують такі складові валових витрат, що не підлягають керуванню з боку керівництва підприємства, наприклад, податки, обов'язкові відрахування в соціальні фонди. І чим вище будуть їхні процентні ставки, тим складніше буде працюватися підприємству. Подібні витрати включаються в змінні витрати, а отже з їхнім ростом величина параметра р буде зменшуватися.

Розглянемо випадок чистої конкуренції. Спробуємо знайти зв’язок між параметром конкурентоспроможності р_>і> та кількістю підприємств на ринку n при умові, що всі інші параметри системи сталі та на ринку працює n однакових підприємств, тобто вони мають однакові параметри р_>і >= p, х_>i>_>0 >= х_>0>, х_>i>(t0) = x(t0), _>i>. В цьому випадку рівні пропозиції всіх підприємств однакові і графіки, що ілюструють динаміку їх пропозицій однакові і зливаються в одну лінію (малюнок 4.1 ).

Проаналізуємо більш докладно цю ситуацію. Зі збільшенням кількості компаній на конкретному ринку, доля прибутку кожної з них буде зменшуватись. Оскільки будь-який ринок обмежений, то з зростанням його насиченості, при рівних можливостях підприємства, що працюють на ньому, будуть змушені ділити прибуток між собою на рівні частини, тобто чим більше суб’єктів, тим менша доля ринку припадає на кожного. Очевидно, що при деякій їх кількості, діяльність кожного з них стане збитковою.

Д
ля знаходження зв’язку між n та p_>i> розглянемо граничний випадок, коли графіки виробничих затрат та цінового коефіціента мають лише одну спільну точку (мал. 4.2). В цьому випадку замінимо у виразі (1.2):

Вираз (1.2) матиме вигляд:

Прирівняємо виробничі затрати F та ціновий коефіціент C:

З цього рівняння отримуємо квадратне рівняння для точок перетину х. Оскільки нас цікавить випадок дотику, тобто коли рівняння має один розв’язок, прирівняємо дискримінант до нуля. Отримаємо вираз:

Легко бачити, що вираз для n має вигляд:

Отже, ми отримали залежність між параметром конкурентоспроможності р_>і> та кількістю підприємств на ринку n. Взагалі конкурентоспроможність характеризує його якості у порівнянні з аналогічними товарами інших виробників і можливість продаватися на ринку за ціною не нижчою за середньоринкову. Більш конкурентоспроможний товар краще відповідає вимогам ринку і виробляється та продається, як правило, з меншими затратами. Існує багато шляхів зменшення витрат. Наприклад, підвищенням ефективності керування та використання ресурсів, впровадженням нових ресурсозберігаючих технологій, автоматизація процесу виробництва. Все це характеризується параметром р_>і>. Дійсно, чим більше р_>і >, тим ефективніше працює підприємство,бо його витрати на одиницю продукції менші.

На малюнку 4.3 зображено графік залежності n від p, при х_>0 >= ; d = 0,2. А на малюнку 4.4 графік логарифмічної залежності. Можемо бачити, що при p0 кількість підприємств, що можуть працювати на ринку одночасно і отримувати прибуток, безмежно зростає. При збільшенні p до безмежності гранична кількість підприємств прямує до певного значення.

Граничне значення n в цьому випадку дорівнює:

Мінімум функції (4.4) дорівнює 1. З формули (4.4) випливає, що значення р в цій точці дорівнює:

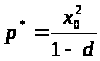
Це є те граничне значення параметру конкурентоспроможності, при якому відбувається перехід з області малих підприємств в область великих при збільшенні р.

Тобто, якщо р<p^* то ми маємо справу з малими суб’єктами ринку(на графіку зліва від мінімуму). Це можуть бути приватні підприємці або дрібні торгівельні фірми. В якості прикладу можна розглянути речовий ринок. Як відомо, на ньому працюють багато ідентичних суб’єктів (продавців), що пропонують однотипні товари. Постійні витрати складає щомісячна платня за торгівельне місце, що є малою порівняно з обсягом закупок товару (змінні витрати), наслідком чого є мала величина параметру р_>і>. Для цієї області характерним є те, що при зменшенні р кількість підприємств може збільшуватись майже необмежено. Безперечно, доля кожного з суб’єктів ринку, а отже і прибуток, будуть зменшуватись.

З іншого боку, при р>p^* ми маємо справу з великими підприємствами (на графіку зправа від мінімуму). Як видно, кількість абсолютно ідентичних підприємств, що працюють на конкретному ринку, росте зі збільшенням параметру конкурентоспроможності кожного з них. Це є закономірним з огляду на те, що зі збільшенням р зростає ефективність виробництва, тобто темп зменшення змінних витрат перевищує зростання постійних, і більша кількість підприємств має змогу одночасно працювати і отримувати прибуток на ринку. Прибуток на одиницю продукції визначається як різниця між ціною та середніми витратами на одиницю продукції. Це характерно для високотехнологічних галузей народного господарства.

Характерним для цієї області є існування і єдиність границі функції (15). Існування границі пояснюється тим, що ефективність виробництва не можна безмежно підвищувати. Легко бачити, що:

Граничні випадки зображені на малюнку 4.5 (d=1) і 4.6 (d=0). В першому випадку, при d=1, отримуємо :

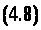
В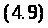

другому випадку, при d=0, отримуємо:

Отже, в якості висновку можна додати, що у випадку, коли дефіцит на ринку дорівнює 1 (d=1), туди можуть входити підприємства з будь-якими значеннями параметру конкуренто-спроможності ( р ). Адже ринок порожній і конкурентів немає. Саме час входити і отримувати надприбутки. Безумовно, кількість підприємств, які можуть одночасно входити на ринок е є безмежною і про це яскраво говорить малюнок 4.5. Але як свідчить статистика, одночасний вхід на новий ринок кількох підприємств відбувається дуже рідко. Завжди хтось намагається бути першим!

А от у випадку, коли ринок вже заповнений (d=0), успішний вхід можливий тільки на такі ринки, де працюючі підприємства мають р<p* . Цей факт пояснюється тим, що коли р<p* , ми маємо справу практично з ринком чистої конкуренції і поява на ньому нового підприємства лише трішки знизить долю ринку кожного з вже працюючих. До кардинальних змін така подія не призведе, звісно за умови, що всі інші параметри лишаються незмінними. Зовсім інша річ відбувається на ринку, коли р>p* . В цьому випадку більше ніж одному тут робити нічого і малюнок 4.6 яскраво ілюструє це. Звісно, якщо ви маєте нову технологію, що здатна зменшити ваші витрати, а з ними і величину р, тоді вперед, спробуйте задавити монополіста!

5. Дослідження моделі при малих значеннях р.

Проаналізуємо більш докладно ситуацію, коли значення параметру конкурентоспроможності підприємств малі, тобто р<p^* (див. вираз 4.6). Як відзначалося раніше, на такому ринку можуть працювати, наприклад, приватні підприємці або дрібні торговці. Це є висококонкурентний ринок, де підприємства цілком залежать від ситуації на ринку. При таких умовах постійні витрати необхідно зводити до мінімуму, а більшу частину витрат складають змінні. Це характерно для ринків товарів широкого вжитку, продовольчих товарів та товарів першої необхідності.

На малюнку 5.1 зображена данаміка 5-ти підприємств з наступними параметрами: d = 0,2;

а) x_>i0> = 0,01; p_>i> = 0,000l2; х_>i>(t0) = 0,03;  = 0,8;

б) x_>i0> = 0,01; p_>i> = 0,000l; х_>i>(t0) = 0,06;  = 0,8;

в) x_>i0> = 0,01; p_>i> = 0,00008; х_>i>(t0) = 0,05;  = 0,8;

г) x_>i0> = 0,01; p_>i> = 0,00006; х_>i>(t0) = 0,04;  = 0,8;

д) x_>i0> = 0,01; p_>i> = 0,0000l; х_>i>(t0) = 0,03;  = 0,8.

Як видно з графіку, виживає підприємство д), яке має найменше значення параметру конкурентоспроможності р = 0,00001. Це свідчить про те, що умовою успішної діяльності підприємства на такому ринку є максимальна мобільність капіталу. Іншими словами, як тільки компанія починає збільшувати долю основних фондів в структурі капіталу, вона ризикує втратити можливість адекватно та швидко реагувати на зміни в ринковій ситуації.

Прикладом такого ринку можуть бути дрібні продавці на стихійних базарах, скажімо жінки, що продають різноманітні пиріжки, булочки та інші продукти харчування. За умови знаходження джерела більш дешевої сировини (борошно, цукор, дріжжі та ін.) такий торговець має змогу знизити ціну на свій товар, при цьому через зменшення змінних витрат його параметр конкурентоспроможності збільшиться. Ті торговці, що не зможуть знизити свої витрати, будуть змушені вийти з ринку через збитковість діяльності за старою схемою. На ринку залишаться лише ті, хто знайде шляхи для пристосування до нових умов. З цього видно, що кількість продавців на ринку з високою конкуренцією зменшується з ростом параметру конкурентоспроможності.

У випадку ж, коли ніхто інший не зможе пристосуватися до нового ринку, цей ринок може перетворитися на монополію. Значення параметра конкурентоспроможності монополіста визначається виразом (4.6). В такій ситуації з боку держави буде застосовано регулювання цін та інші антимонопольні заходи, щоб дати змогу працювати і отримувати прибуток на ринку іншим підприємцям.

Розглянемо випадок, коли на ринок входить новий суб’єкт. Оскільки бар’єр входу на цей ринок невисокий, то вхід на нього не викличе великих складностей. При цьому незначно зменшиться доля ринку кожного з суб’єктів господарювання.

З наведених прикладів видно, що зі збільшенням параметру конкурентоспроможності кількість одночасно працюючих на ринку підприємств зменшується (малюнок 4.4 при р<p^* ).

Дослідимо область беззбиткової діяльності на такому ринку (малюнок 1.3). Як видно з малюнку, область беззбитковості ( ціна перевищує витрати ) обмежена справа точкою x_>i>_>0> .

Як було зазначено вище, границі інтервалу беззбитковості зв’язані співвідношенням :

Очевидно, що при р<p^*  x_>i>_>0> < x_>if> і точка x_>i>_>0> є стійким рішенням системи (1.13). Доведемо цей факт, для випадку n=1.

З

апишемо результат лінеаризації системи (1.13) :

П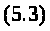
ідставивши в (5.2) x_>i> = x_>i>_>0> отримаємо :

Л
інійне диференційне рівняння (5.3) стійке, якщо:

Це еквівалентно наступному співвідношенню:

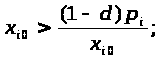
Для тих значень р, що ми розглядаємо (р<p^*), цей вираз є істиною. Отже, при відсутності конкурентів, обсяг виробництва будь-якого підприємства прямуватиме до x_>i>_>0> . Це можна бачити на малюнку 5.1, де обсяг виробництва підприємства, що вижило після збанкрутування всіх інших, встановлюється на рівні x_>i>_>0> .

І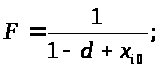
снує граничний випадок, коли параметр р дуже низький. Це проілюстровано на малюнку 5.2 (р=0,0000001; n=1): виробничі витрати, починаючи з дуже малих об’ємів встановлюється на постійному рівні. З формули (1.7) легко отримати вираз для цього граничного значення:

Висновки.

В даній дипломній роботі була побудована імітаційна модель взаємодії підприємства з ринком, що дозволяє прогнозувати обсяги вироництва в будь-який момент в майбутньому. Проаналізувавши отриману модель, можна стверджувати, що прогнози отримані при застосуванні моделі співпадають з тим, що можна отримати з економічної теорії для системи, що діє згідно з ринковими законами.

Детально було досліджеено ринок на якому діють підприємства з низьким рівнем параметра конкурентоспроможності, тобто бар’єр входу невисокий і процес виникнення нових підприємств на ньому не викликає труднощів. Прикладом такого ринку можуть слугувати стихійні базари. В ході дослідження було виявлено, що на такому ринку найкращому становищу знаходиться той підприємець, який має нижчий рівень параметра конкурентоспроможності.

Для застосування моделі на практиці, можна використовувати існуючі в економіці методики обчислення місткісті та дефіциту ринка, внутрішніх показників підприємства – постійних та змінних витрат, рівня беззбитковості та інших. Використавши в моделі ці дані для певної галузі отримаємо прогноз динаміки обсягу виробництва для цієї галузі. Важливим є те, що динаміку можна прослідкувати при різних варіантах розподілення витрат на кожному підприємстві.

Такий прогноз необхідний для успішного керівництва підприємством, особливо при прийнятті рішень, наслідки від яких проявляться лише в майбутньому.

Графічне представлення динаміки легко може бути отримане за допомогою прикладних програмних засобів (в дипломній роботі для цього використовується Excel).

Звичайно, модель не є ідеальною, бо не враховує всі можливі фактори, що реально існують і суттєво впливають на систему (державне регулювання, коливання курсів валют, зміна банківських відсотків за кредит та інш.). Найбільш ефективною отримана модель буде для підприємств, працюючих на ринках з мінімальним втручанням держави. Структура побудованої моделі дозволяє вводити нові параметри, за допомогою яких може бути врахований вплив будь-яких факторів, що нас цікавлять. Це забезпечує можливості розвитку та вдосконалення моделі в майбутньому та дослідження за допомогою неї більш складних систем.

начальное условие	предприятие 1	предприятие 2	предприятие 3
Xi0	0,007	0,007	0,007
Pi	0,019	0,019	0,019
Xi(t0)	0,5	0,5	0,5
ti	1	0,8	0,7
d	0,2	0,2	0,2
n	8

0,4998806	0,499851	0,499829
0,5356084	0,544507	0,550863
0,564094	0,580812	0,592924
0,5864824	0,609817	0,626916
0,603892	0,632699	0,654005
0,6173178	0,650587	0,675383
0,6275995	0,664476	0,69214
0,6354236	0,675207	0,705218
0,6413401	0,683466	0,715401
0,6457829	0,689804	0,723325
0,6490914	0,694657	0,729496
0,6515291	0,698367	0,734315
0,6532993	0,701199	0,738094
0,6545587	0,703357	0,741075
0,6554272	0,705001	0,743446
0,655997	0,70625	0,74535
0,6563381	0,707199	0,746899
0,6565044	0,707919	0,748178
0,6565368	0,708463	0,749251
0,6564664	0,708874	0,750168
0,6563171	0,709183	0,750968
0,6561069	0,709414	0,751678
0,6558497	0,709586	0,752322
0,6555558	0,709712	0,752915
0,6552333	0,709804	0,753471
0,6548882	0,709869	0,754
0,6545252	0,709914	0,754509
0,6541477	0,709944	0,755003
0,6537584	0,709961	0,755488
0,6533594	0,709969	0,755966
0,652952	0,70997	0,756441
0,6525375	0,709965	0,756913
0,6521168	0,709955	0,757385
0,6516905	0,709942	0,757857
0,6512591	0,709926	0,758331
0,6508229	0,709908	0,758807
0,6503823	0,709888	0,759285
0,6499374	0,709866	0,759767
0,6494885	0,709842	0,760252
0,6490355	0,709818	0,760741
0,6485786	0,709792	0,761234
0,6481178	0,709765	0,76173
0,6476531	0,709737	0,762231
0,6471846	0,709708	0,762736
0,6467122	0,709678	0,763246
0,646236	0,709648	0,76376
0,645756	0,709616	0,764278
0,6452721	0,709584	0,764801
0,6447843	0,709551	0,765329
0,6442926	0,709517	0,765861
0,643797	0,709482	0,766399
0,6432974	0,709446	0,766941
0,6427938	0,709409	0,767488
0,6422862	0,709372	0,768039
0,6417746	0,709333	0,768596
0,6412589	0,709294	0,769158
0,6407391	0,709253	0,769725
0,6402151	0,709212	0,770297
0,639687	0,70917	0,770874
0,6391547	0,709127	0,771456
0,6386182	0,709083	0,772044
0,6380774	0,709038	0,772636
0,6375323	0,708992	0,773234
0,6369829	0,708945	0,773838
0,6364291	0,708897	0,774447
0,6358709	0,708848	0,775061
0,6353083	0,708798	0,775681
0,6347413	0,708746	0,776307
0,6341697	0,708694	0,776938
0,6335936	0,708641	0,777575
0,6330129	0,708586	0,778218
0,6324276	0,708531	0,778866
0,6318377	0,708474	0,77952
0,6312431	0,708416	0,78018
0,6306438	0,708357	0,780846
0,6300398	0,708297	0,781518
0,6294309	0,708236	0,782197
0,6288173	0,708173	0,782881
0,6281987	0,708109	0,783571
0,6275753	0,708044	0,784268
0,6269469	0,707978	0,78497
0,6263136	0,707911	0,785679
0,6256752	0,707842	0,786395
0,6250318	0,707772	0,787117
0,6243833	0,7077	0,787845
0,6237297	0,707627	0,78858
0,6230709	0,707553	0,789322
0,6224069	0,707477	0,79007
0,6217376	0,707401	0,790825
0,6210631	0,707322	0,791586
0,6203832	0,707242	0,792355
0,6196979	0,707161	0,79313
0,6190073	0,707078	0,793913
0,6183111	0,706994	0,794702
0,6176095	0,706908	0,795498
0,6169023	0,706821	0,796302
0,6161896	0,706732	0,797113
0,6154712	0,706642	0,797931
0,6147471	0,70655	0,798756
0,6140174	0,706457	0,799589
0,6132819	0,706361	0,800429
0,6125405	0,706265	0,801277
0,6117934	0,706166	0,802133
0,6110403	0,706066	0,802996
0,6102813	0,705964	0,803866
0,6095163	0,70586	0,804745
0,6087453	0,705755	0,805631
0,6079682	0,705648	0,806526
0,607185	0,705539	0,807428
0,6063957	0,705428	0,808339
0,6056001	0,705315	0,809257
0,6047982	0,705201	0,810184
0,6039901	0,705085	0,811119
0,6031756	0,704966	0,812062
0,6023547	0,704846	0,813014
0,6015273	0,704724	0,813975
0,6006934	0,7046	0,814944
0,599853	0,704473	0,815921
0,5990059	0,704345	0,816908
0,5981522	0,704215	0,817903
0,5972919	0,704082	0,818907
0,5964247	0,703948	0,81992
0,5955507	0,703811	0,820942
0,5946699	0,703673	0,821973
0,5937822	0,703532	0,823013
0,5928875	0,703388	0,824063
0,5919858	0,703243	0,825122
0,591077	0,703095	0,82619
0,5901611	0,702945	0,827268
0,5892381	0,702793	0,828356
0,5883078	0,702638	0,829453
0,5873702	0,702481	0,83056
0,5864253	0,702321	0,831677
0,5854729	0,702159	0,832803
0,5845132	0,701995	0,83394
0,5835459	0,701828	0,835087
0,582571	0,701659	0,836244
0,5815886	0,701487	0,837411
0,5805984	0,701312	0,838589
0,5796005	0,701135	0,839777
0,5785949	0,700955	0,840976
0,5775813	0,700772	0,842185
0,5765599	0,700587	0,843406
0,5755305	0,700399	0,844637
0,5744931	0,700208	0,845879
0,5734475	0,700014	0,847131
0,5723938	0,699818	0,848395
0,571332	0,699618	0,849671
0,5702618	0,699416	0,850957
0,5691833	0,699211	0,852255
0,5680964	0,699003	0,853565
0,567001	0,698791	0,854886
0,5658972	0,698577	0,856218
0,5647847	0,698359	0,857563
0,5636636	0,698139	0,858919
0,5625338	0,697915	0,860287
0,5613952	0,697688	0,861668
0,5602477	0,697458	0,863061
0,5590914	0,697225	0,864466
0,557926	0,696988	0,865883
0,5567516	0,696748	0,867313
0,5555682	0,696504	0,868755
0,5543755	0,696257	0,870211
0,5531736	0,696007	0,871679
0,5519624	0,695753	0,87316
0,5507418	0,695496	0,874654
0,5495118	0,695235	0,876161
0,5482722	0,69497	0,877682
0,5470231	0,694702	0,879216
0,5457643	0,69443	0,880763
0,5444957	0,694154	0,882324
0,5432174	0,693874	0,883899
0,5419292	0,693591	0,885488
0,540631	0,693303	0,88709
0,5393229	0,693012	0,888707
0,5380046	0,692717	0,890338
0,5366762	0,692417	0,891983
0,5353375	0,692114	0,893642
0,5339886	0,691807	0,895317
0,5326292	0,691495	0,897005
0,5312594	0,691179	0,898709
0,529879	0,690859	0,900428
0,5284881	0,690535	0,902161
0,5270864	0,690206	0,90391
0,525674	0,689873	0,905674
0,5242507	0,689536	0,907454
0,5228165	0,689194	0,909249
0,5213713	0,688847	0,91106
0,519915	0,688496	0,912886
0,5184475	0,68814	0,914729
0,5169688	0,68778	0,916587
0,5154788	0,687414	0,918462
0,5139774	0,687044	0,920353
0,5124644	0,68667	0,922261
0,51094	0,68629	0,924185
0,5094038	0,685905	0,926126
0,507856	0,685515	0,928084
0,5062963	0,685121	0,930059
0,5047247	0,684721	0,932052
0,5031411	0,684316	0,934061
0,5015455	0,683905	0,936088
0,4999376	0,68349	0,938132
0,4983176	0,683069	0,940195
0,4966852	0,682642	0,942275
0,4950404	0,682211	0,944373
0,4933831	0,681773	0,94649
0,4917132	0,68133	0,948624
0,4900306	0,680882	0,950778
0,4883353	0,680428	0,952949
0,4866271	0,679968	0,95514
0,4849059	0,679502	0,95735
0,4831717	0,67903	0,959578
0,4814243	0,678553	0,961826
0,4796638	0,678069	0,964094
0,4778899	0,67758	0,96638
0,4761026	0,677084	0,968687
0,4743018	0,676582	0,971013
0,4724874	0,676074	0,97336
0,4706593	0,675559	0,975727
0,4688174	0,675038	0,978114
0,4669616	0,674511	0,980521
0,4650919	0,673977	0,982949
0,4632081	0,673436	0,985399
0,4613101	0,672889	0,987869
0,4593978	0,672335	0,99036
0,4574712	0,671774	0,992873
0,4555301	0,671207	0,995407
0,4535744	0,670632	0,997963
0,4516041	0,67005	1,000541
0,449619	0,669462	1,00314
0,447619	0,668866	1,005762
0,4456041	0,668263	1,008407
0,4435741	0,667652	1,011074
0,441529	0,667035	1,013763
0,4394685	0,66641	1,016476
0,4373927	0,665777	1,019212
0,4353014	0,665136	1,021971
0,4331945	0,664488	1,024753
0,4310719	0,663833	1,02756
0,4289336	0,663169	1,03039
0,4267793	0,662497	1,033244
0,424609	0,661818	1,036122
0,4224226	0,66113	1,039025
0,42022	0,660434	1,041952
0,418001	0,65973	1,044904
0,4157656	0,659018	1,047881
0,4135137	0,658297	1,050883
0,4112451	0,657568	1,053911
0,4089597	0,65683	1,056964
0,4066574	0,656083	1,060043
0,4043382	0,655328	1,063147
0,4020018	0,654564	1,066278
0,3996483	0,653791	1,069436
0,3972774	0,653009	1,072619
0,394889	0,652218	1,07583
0,3924831	0,651418	1,079068
0,3900596	0,650608	1,082332
0,3876182	0,649789	1,085625
0,385159	0,648961	1,088944
0,3826817	0,648123	1,092292
0,3801863	0,647275	1,095667
0,3776726	0,646418	1,099071
0,3751406	0,64555	1,102503
0,3725901	0,644673	1,105964
0,370021	0,643786	1,109454
0,3674332	0,642889	1,112972
0,3648265	0,641981	1,11652
0,3622008	0,641064	1,120098
0,3595561	0,640136	1,123705
0,3568922	0,639197	1,127342
0,3542089	0,638248	1,131009
0,3515062	0,637288	1,134707
0,3487839	0,636317	1,138436
0,3460419	0,635335	1,142195
0,3432801	0,634342	1,145985
0,3404984	0,633338	1,149807
0,3376966	0,632323	1,15366
0,3348746	0,631297	1,157545
0,3320323	0,630259	1,161462
0,3291695	0,62921	1,165411
0,3262862	0,628149	1,169392
0,3233821	0,627076	1,173406
0,3204573	0,625991	1,177454
0,3175115	0,624895	1,181534
0,3145446	0,623786	1,185648
0,3115565	0,622665	1,189795
0,308547	0,621532	1,193977
0,3055161	0,620387	1,198192
0,3024636	0,619228	1,202442
0,2993894	0,618058	1,206726
0,2962932	0,616874	1,211046
0,2931751	0,615678	1,2154
0,2900349	0,614468	1,21979
0,2868724	0,613246	1,224216
0,2836876	0,61201	1,228677
0,2804801	0,610761	1,233175
0,2772501	0,609499	1,237708

????????? ???????	??????????? 1	??????????? 2	??????????? 3
Xi0	0,01	0,007	0,01
Pi	0,019	0,015	0,025
Xi(t0)	0,5	0,4	0,3
ti	1	0,8	1
d	0,2	0,2	0,2
n	8
0,4997944	0,399788	0,299794
0,5233796	0,436522	0,328451
0,5393531	0,467795	0,354859
0,5488872	0,494038	0,379277
0,5531352	0,515844	0,402017
0,5531348	0,533845	0,4234
0,5497714	0,54864	0,443726
0,5437751	0,560762	0,463262
0,5357346	0,570667	0,482236
0,5261174	0,57873	0,50084
0,5152907	0,58526	0,519234
0,5035412	0,590501	0,537547
0,491092	0,594648	0,555884
0,4781162	0,597851	0,57433
0,4647487	0,60023	0,592951
0,4510947	0,601874	0,611798
0,4372371	0,602854	0,630911
0,4232412	0,603223	0,650322
0,4091596	0,603021	0,670052
0,395035	0,602277	0,690117
0,3809025	0,601017	0,710525
0,3667916	0,599255	0,731283
0,3527275	0,597007	0,752392
0,3387322	0,594283	0,773847
0,3248251	0,591091	0,795646
0,3110235	0,58744	0,817778
0,2973435	0,583335	0,840234
0,2837997	0,578784	0,863002
0,2704056	0,573793	0,886067
0,257174	0,56837	0,909414
0,2441169	0,562523	0,933025
0,2312455	0,556259	0,956882
0,2185704	0,549589	0,980966
0,2061017	0,542522	1,005255
0,1938486	0,53507	1,029728
0,1818199	0,527244	1,054362
0,1700237	0,519058	1,079134
0,1584676	0,510525	1,104019
0,1471584	0,501661	1,128994
0,1361025	0,492481	1,154034
0,1253054	0,483001	1,179113
0,1147722	0,473239	1,204206
0,1045072	0,463212	1,229287
0,094514	0,452938	1,254331
0,0847959	0,442437	1,279312
0,075355	0,431728	1,304206
0,0661933	0,42083	1,328986
0,0573118	0,409764	1,35363
0,0487112	0,398548	1,378111
0,0403913	0,387203	1,402408
0,0323514	0,37575	1,426497
0,0245904	0,364207	1,450356
0,0171064	0,352595	1,473964
0,0098972	0,340933	1,497301
0,00296	0,32924	1,520346
-0,0037086	0,317535	1,543082
-0,0101121	0,305835	1,565492
-0,0162547	0,294159	1,587558
-0,022141	0,282523	1,609265
-0,0277757	0,270944	1,630601
-0,033164	0,259437	1,651552
-0,0383115	0,248017	1,672105
-0,0432238	0,236698	1,692252
-0,0479068	0,225494	1,711982
-0,0523667	0,214417	1,731288
-0,0566098	0,203478	1,750162
-0,0606425	0,192689	1,7686
-0,0644715	0,182059	1,786596
-0,0681032	0,171597	1,804147
-0,0715443	0,161312	1,82125
-0,0748017	0,151211	1,837904
-0,0778819	0,141301	1,85411
-0,0807916	0,131587	1,869866
-0,0835376	0,122074	1,885176
-0,0861264	0,112767	1,90004
-0,0885644	0,103669	1,914463
-0,0908582	0,094784	1,928448
-0,093014	0,086112	1,942
-0,0950381	0,077657	1,955124
-0,0969364	0,069418	1,967825
-0,0987149	0,061397	1,980111
-0,1003795	0,053592	1,991987
-0,1019356	0,046004	2,003462
-0,1033888	0,038632	2,014542
-0,1047443	0,031473	2,025237
-0,1060072	0,024526	2,035553
-0,1071825	0,017789	2,0455
-0,1082749	0,011258	2,055086
-0,109289	0,004932	2,064321
-0,1102292	-0,00119	2,073214
-0,1110998	-0,00712	2,081772
-0,1119047	-0,01285	2,090007
-0,1126478	-0,0184	2,097926
-0,1133329	-0,02375	2,10554
-0,1139635	-0,02893	2,112857
-0,1145429	-0,03392	2,119887
-0,1150744	-0,03874	2,126639
-0,1155609	-0,04339	2,133121
-0,1160055	-0,04788	2,139343
-0,1164108	-0,0522	2,145313
-0,1167795	-0,05637	2,15104
-0,1171139	-0,06039	2,156533
-0,1174166	-0,06426	2,161799
-0,1176896	-0,06798	2,166847
-0,117935	-0,07157	2,171686
-0,1181549	-0,07502	2,176322
-0,118351	-0,07834	2,180763
-0,1185251	-0,08153	2,185017
-0,1186789	-0,0846	2,18909
-0,1188138	-0,08755	2,192991
-0,1189313	-0,09039	2,196725
-0,1190328	-0,09312	2,200299
-0,1191196	-0,09574	2,203719
-0,1191928	-0,09825	2,206993
-0,1192536	-0,10067	2,210125
-0,1193029	-0,10299	2,213121
-0,1193418	-0,10522	2,215987
-0,1193711	-0,10736	2,218728
-0,1193918	-0,10942	2,22135
-0,1194046	-0,11139	2,223858
-0,1194102	-0,11328	2,226255
-0,1194092	-0,1151	2,228548
-0,1194025	-0,11684	2,23074
-0,1193904	-0,11852	2,232836
-0,1193736	-0,12012	2,234839
-0,1193526	-0,12166	2,236754
-0,1193278	-0,12313	2,238585
-0,1192997	-0,12455	2,240335
-0,1192687	-0,12591	2,242007
-0,1192351	-0,12721	2,243606
-0,1191992	-0,12845	2,245134
-0,1191614	-0,12965	2,246594
-0,119122	-0,1308	2,24799
-0,1190812	-0,13189	2,249324
-0,1190393	-0,13295	2,250598
-0,1189964	-0,13396	2,251816
-0,1189529	-0,13492	2,25298
-0,1189088	-0,13585	2,254093
-0,1188643	-0,13674	2,255156
-0,1188196	-0,13759	2,256172
-0,1187748	-0,13841	2,257143
-0,11873	-0,13919	2,25807
-0,1186854	-0,13994	2,258957
-0,1186411	-0,14066	2,259804
-0,118597	-0,14135	2,260614
-0,1185534	-0,142	2,261388
-0,1185103	-0,14264	2,262128
-0,1184677	-0,14324	2,262834
-0,1184258	-0,14382	2,26351
-0,1183844	-0,14437	2,264155
-0,1183438	-0,14491	2,264772

начальное условие	предприятие 1	предприятие 2	предприятие 3
Xi0	0,007	0,007	0,007
Pi	0,019	0,019	0,019
Xi(t0)	0,5	0,5	0,5
ti	1	0,8	0,7
d	0,2	0,2	0,2
n	8
0,4998806	0,499851	0,499829
0,5356084	0,544507	0,550863
0,564094	0,580812	0,592924
0,5864824	0,609817	0,626916
0,603892	0,632699	0,654005
0,6173178	0,650587	0,675383
0,6275995	0,664476	0,69214
0,6354236	0,675207	0,705218
0,6413401	0,683466	0,715401
0,6457829	0,689804	0,723325
0,6490914	0,694657	0,729496
0,6515291	0,698367	0,734315
0,6532993	0,701199	0,738094
0,6545587	0,703357	0,741075
0,6554272	0,705001	0,743446
0,655997	0,70625	0,74535
0,6563381	0,707199	0,746899
0,6565044	0,707919	0,748178
0,6565368	0,708463	0,749251
0,6564664	0,708874	0,750168
0,6563171	0,709183	0,750968
0,6561069	0,709414	0,751678
0,6558497	0,709586	0,752322
0,6555558	0,709712	0,752915
0,6552333	0,709804	0,753471
0,6548882	0,709869	0,754
0,6545252	0,709914	0,754509
0,6541477	0,709944	0,755003
0,6537584	0,709961	0,755488
0,6533594	0,709969	0,755966
0,652952	0,70997	0,756441
0,6525375	0,709965	0,756913
0,6521168	0,709955	0,757385
0,6516905	0,709942	0,757857
0,6512591	0,709926	0,758331
0,6508229	0,709908	0,758807
0,6503823	0,709888	0,759285
0,6499374	0,709866	0,759767
0,6494885	0,709842	0,760252
0,6490355	0,709818	0,760741
0,6485786	0,709792	0,761234
0,6481178	0,709765	0,76173
0,6476531	0,709737	0,762231
0,6471846	0,709708	0,762736
0,6467122	0,709678	0,763246
0,646236	0,709648	0,76376
0,645756	0,709616	0,764278
0,6452721	0,709584	0,764801
0,6447843	0,709551	0,765329
0,6442926	0,709517	0,765861
0,643797	0,709482	0,766399
0,6432974	0,709446	0,766941
0,6427938	0,709409	0,767488
0,6422862	0,709372	0,768039
0,6417746	0,709333	0,768596
0,6412589	0,709294	0,769158
0,6407391	0,709253	0,769725
0,6402151	0,709212	0,770297
0,639687	0,70917	0,770874
0,6391547	0,709127	0,771456
0,6386182	0,709083	0,772044
0,6380774	0,709038	0,772636
0,6375323	0,708992	0,773234
0,6369829	0,708945	0,773838
0,6364291	0,708897	0,774447
0,6358709	0,708848	0,775061
0,6353083	0,708798	0,775681
0,6347413	0,708746	0,776307
0,6341697	0,708694	0,776938
0,6335936	0,708641	0,777575
0,6330129	0,708586	0,778218
0,6324276	0,708531	0,778866
0,6318377	0,708474	0,77952
0,6312431	0,708416	0,78018
0,6306438	0,708357	0,780846
0,6300398	0,708297	0,781518
0,6294309	0,708236	0,782197
0,6288173	0,708173	0,782881
0,6281987	0,708109	0,783571
0,6275753	0,708044	0,784268
0,6269469	0,707978	0,78497
0,6263136	0,707911	0,785679
0,6256752	0,707842	0,786395
0,6250318	0,707772	0,787117
0,6243833	0,7077	0,787845
0,6237297	0,707627	0,78858
0,6230709	0,707553	0,789322
0,6224069	0,707477	0,79007
0,6217376	0,707401	0,790825
0,6210631	0,707322	0,791586
0,6203832	0,707242	0,792355
0,6196979	0,707161	0,79313
0,6190073	0,707078	0,793913
0,6183111	0,706994	0,794702
0,6176095	0,706908	0,795498
0,6169023	0,706821	0,796302
0,6161896	0,706732	0,797113
0,6154712	0,706642	0,797931
0,6147471	0,70655	0,798756
0,6140174	0,706457	0,799589
0,6132819	0,706361	0,800429
0,6125405	0,706265	0,801277
0,6117934	0,706166	0,802133
0,6110403	0,706066	0,802996
0,6102813	0,705964	0,803866
0,6095163	0,70586	0,804745
0,6087453	0,705755	0,805631
0,6079682	0,705648	0,806526
0,607185	0,705539	0,807428
0,6063957	0,705428	0,808339
0,6056001	0,705315	0,809257
0,6047982	0,705201	0,810184
0,6039901	0,705085	0,811119
0,6031756	0,704966	0,812062
0,6023547	0,704846	0,813014
0,6015273	0,704724	0,813975
0,6006934	0,7046	0,814944
0,599853	0,704473	0,815921
0,5990059	0,704345	0,816908
0,5981522	0,704215	0,817903
0,5972919	0,704082	0,818907
0,5964247	0,703948	0,81992
0,5955507	0,703811	0,820942
0,5946699	0,703673	0,821973
0,5937822	0,703532	0,823013
0,5928875	0,703388	0,824063
0,5919858	0,703243	0,825122
0,591077	0,703095	0,82619
0,5901611	0,702945	0,827268
0,5892381	0,702793	0,828356
0,5883078	0,702638	0,829453
0,5873702	0,702481	0,83056
0,5864253	0,702321	0,831677
0,5854729	0,702159	0,832803
0,5845132	0,701995	0,83394
0,5835459	0,701828	0,835087
0,582571	0,701659	0,836244
0,5815886	0,701487	0,837411
0,5805984	0,701312	0,838589
0,5796005	0,701135	0,839777
0,5785949	0,700955	0,840976
0,5775813	0,700772	0,842185
0,5765599	0,700587	0,843406
0,5755305	0,700399	0,844637
0,5744931	0,700208	0,845879
0,5734475	0,700014	0,847131
0,5723938	0,699818	0,848395
0,571332	0,699618	0,849671
0,5702618	0,699416	0,850957
0,5691833	0,699211	0,852255
0,5680964	0,699003	0,853565
0,567001	0,698791	0,854886
0,5658972	0,698577	0,856218
0,5647847	0,698359	0,857563
0,5636636	0,698139	0,858919
0,5625338	0,697915	0,860287
0,5613952	0,697688	0,861668
0,5602477	0,697458	0,863061
0,5590914	0,697225	0,864466
0,557926	0,696988	0,865883
0,5567516	0,696748	0,867313
0,5555682	0,696504	0,868755
0,5543755	0,696257	0,870211
0,5531736	0,696007	0,871679
0,5519624	0,695753	0,87316
0,5507418	0,695496	0,874654
0,5495118	0,695235	0,876161
0,5482722	0,69497	0,877682
0,5470231	0,694702	0,879216
0,5457643	0,69443	0,880763
0,5444957	0,694154	0,882324
0,5432174	0,693874	0,883899
0,5419292	0,693591	0,885488
0,540631	0,693303	0,88709
0,5393229	0,693012	0,888707
0,5380046	0,692717	0,890338
0,5366762	0,692417	0,891983
0,5353375	0,692114	0,893642
0,5339886	0,691807	0,895317
0,5326292	0,691495	0,897005
0,5312594	0,691179	0,898709
0,529879	0,690859	0,900428
0,5284881	0,690535	0,902161
0,5270864	0,690206	0,90391
0,525674	0,689873	0,905674
0,5242507	0,689536	0,907454
0,5228165	0,689194	0,909249
0,5213713	0,688847	0,91106
0,519915	0,688496	0,912886
0,5184475	0,68814	0,914729
0,5169688	0,68778	0,916587
0,5154788	0,687414	0,918462
0,5139774	0,687044	0,920353
0,5124644	0,68667	0,922261
0,51094	0,68629	0,924185
0,5094038	0,685905	0,926126
0,507856	0,685515	0,928084
0,5062963	0,685121	0,930059
0,5047247	0,684721	0,932052
0,5031411	0,684316	0,934061
0,5015455	0,683905	0,936088
0,4999376	0,68349	0,938132
0,4983176	0,683069	0,940195
0,4966852	0,682642	0,942275
0,4950404	0,682211	0,944373
0,4933831	0,681773	0,94649
0,4917132	0,68133	0,948624
0,4900306	0,680882	0,950778
0,4883353	0,680428	0,952949
0,4866271	0,679968	0,95514
0,4849059	0,679502	0,95735
0,4831717	0,67903	0,959578
0,4814243	0,678553	0,961826
0,4796638	0,678069	0,964094
0,4778899	0,67758	0,96638
0,4761026	0,677084	0,968687
0,4743018	0,676582	0,971013
0,4724874	0,676074	0,97336
0,4706593	0,675559	0,975727
0,4688174	0,675038	0,978114
0,4669616	0,674511	0,980521
0,4650919	0,673977	0,982949
0,4632081	0,673436	0,985399
0,4613101	0,672889	0,987869
0,4593978	0,672335	0,99036
0,4574712	0,671774	0,992873
0,4555301	0,671207	0,995407
0,4535744	0,670632	0,997963
0,4516041	0,67005	1,000541
0,449619	0,669462	1,00314
0,447619	0,668866	1,005762
0,4456041	0,668263	1,008407
0,4435741	0,667652	1,011074
0,441529	0,667035	1,013763
0,4394685	0,66641	1,016476
0,4373927	0,665777	1,019212
0,4353014	0,665136	1,021971
0,4331945	0,664488	1,024753
0,4310719	0,663833	1,02756
0,4289336	0,663169	1,03039
0,4267793	0,662497	1,033244
0,424609	0,661818	1,036122
0,4224226	0,66113	1,039025
0,42022	0,660434	1,041952
0,418001	0,65973	1,044904
0,4157656	0,659018	1,047881
0,4135137	0,658297	1,050883
0,4112451	0,657568	1,053911
0,4089597	0,65683	1,056964
0,4066574	0,656083	1,060043
0,4043382	0,655328	1,063147
0,4020018	0,654564	1,066278
0,3996483	0,653791	1,069436
0,3972774	0,653009	1,072619
0,394889	0,652218	1,07583
0,3924831	0,651418	1,079068
0,3900596	0,650608	1,082332
0,3876182	0,649789	1,085625
0,385159	0,648961	1,088944
0,3826817	0,648123	1,092292
0,3801863	0,647275	1,095667
0,3776726	0,646418	1,099071
0,3751406	0,64555	1,102503
0,3725901	0,644673	1,105964
0,370021	0,643786	1,109454
0,3674332	0,642889	1,112972
0,3648265	0,641981	1,11652
0,3622008	0,641064	1,120098
0,3595561	0,640136	1,123705
0,3568922	0,639197	1,127342
0,3542089	0,638248	1,131009
0,3515062	0,637288	1,134707
0,3487839	0,636317	1,138436
0,3460419	0,635335	1,142195
0,3432801	0,634342	1,145985
0,3404984	0,633338	1,149807
0,3376966	0,632323	1,15366
0,3348746	0,631297	1,157545
0,3320323	0,630259	1,161462
0,3291695	0,62921	1,165411
0,3262862	0,628149	1,169392
0,3233821	0,627076	1,173406
0,3204573	0,625991	1,177454
0,3175115	0,624895	1,181534
0,3145446	0,623786	1,185648
0,3115565	0,622665	1,189795
0,308547	0,621532	1,193977
0,3055161	0,620387	1,198192
0,3024636	0,619228	1,202442
0,2993894	0,618058	1,206726
0,2962932	0,616874	1,211046
0,2931751	0,615678	1,2154
0,2900349	0,614468	1,21979
0,2868724	0,613246	1,224216
0,2836876	0,61201	1,228677
0,2804801	0,610761	1,233175
0,2772501	0,609499	1,237708

4