Затухание ЭМВ при распространении в средах с конечной проводимостью (работа 2)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Харьковский национальный университет
им. В.Н. Каразина
Радиофизический факультет
КУРСОВАЯ РАБОТА
ПО ЭЛЕКТРОДИНАМИКЕ
«Затухание ЭМВ при распространении в средах с конечной проводимостью»
Руководитель:
Колчигин Н.Н.
Студент группы РР-32
Бойко Ю.В.
Харьков 2004
Содержание
Введение 4
Основная часть 5
1. Вывод уравнений для плоских волн 5
2. Связь характеристик распространения с параметрами среды 9
3. Вычисление затухания в данной среде 14
Список использованной литературы 15
ЗАДАНИЕ
1.Изучить общие сведения и формулы.
2.Построить зависимость электрической компоненты поля от глубины проникновения.
3.Вычислить затухание на глубине Н=0,5 м, =10 м, в пресной воде (=80, =10-3 См/м)
Введение
Распространение электромагнитных волн широко рассматривается в литературе, но в ней большое внимание уделяется распространению волн в диспергирующих средах и законам геометрической оптики. В данной работе рассматривается связь характеристик распространения с параметрами среды и затухание элекромагнитных волн в средах с конечной проводимостью
Основная часть
1. Вывод уравнений для плоских волн
Рассмотрим электромагнитный
волновой процесс, векторы
 и
и
 которого
могут быть представлены в виде
которого
могут быть представлены в виде
 =
= (,t),
(,t),
 =
= (,t)
(1.1)
(,t)
(1.1)

Рис. 1.1. Направление распространения плоской волны
Здесь (рис. 1.1.)
 есть расстояние от начала
координатной системы до плоскости
есть расстояние от начала
координатной системы до плоскости

а
 является постоянным единичным вектором.
Так как производные по координатам
будут равны
является постоянным единичным вектором.
Так как производные по координатам
будут равны
 и т. д., то
и т. д., то

 (1.2)
(1.2)
 (1.3)
(1.3)

Следовательно, для плоской волны уравнения Максвелла принимают вид

 (1.4)
(1.4)
 ,
,

Последние два уравнения
означают независимость проекций
 и
и
 на направление распространения от
координаты ,
т. е. E>>
=const
и H>>=const
в данный момент времени. Исследуем их
поведение во времени. Для этого второе
уравнение (1.4) умножим скалярно на
на направление распространения от
координаты ,
т. е. E>>
=const
и H>>=const
в данный момент времени. Исследуем их
поведение во времени. Для этого второе
уравнение (1.4) умножим скалярно на
 :
:

Так как

то
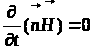
и


или
 ,
т.е. dH>>>
>= 0, H>>
= const. Для исследования
поведения E>>
умножим скалярно первое из уравнений
(1.4) на
,
т.е. dH>>>
>= 0, H>>
= const. Для исследования
поведения E>>
умножим скалярно первое из уравнений
(1.4) на
 :
:

Так как
 ,
получаем
,
получаем

Прибавим к этому равенству





Следовательно, при конечной компонента E>> экспоненциально убывает со временем, т. е. статическое электрическое поле не может поддерживаться внутри проводника.
Найдем уравнения для
 и
и
 отдельно.
Для этого продифференцируем по t
первое из уравнений (1.4)
отдельно.
Для этого продифференцируем по t
первое из уравнений (1.4)


Найдем
 из второго из уравнений (1.4),
продифференцировав его по :
из второго из уравнений (1.4),
продифференцировав его по :

Получаем


откуда

 ,
так как
,
так как


Отсюда следует
 (1.6)
(1.6)
Аналогично
 >
> (1.7)
>
> (1.7)
Эти уравнения можно решить методом
разделения переменных, идем решение
для комплексной амплитуды Е поля
 ,
Положив
,
Положив
E=f>1>()f>2>()
Получаем

 (1.8)
(1.8)
Общее решение для f>1> будет

Частное решение для f>2> возьмем в виде

Таким образом, решением
для
 будет выражение
будет выражение

Решая уравнение (1.7),
получим аналогичное решение для


Подставив эти значения во второе из уравнений (1.4), получим

откуда

Так как в этом равенстве может принимать любые значения, коэффициенты при экспонентах должны равняться нулю:


Поэтому

 (1.9)
(1.9)
Отсюда следует (
 )=0
(так как (
)=0
(так как ( [
[
 ])=0),
т. е. векторы
])=0),
т. е. векторы
 и
и
 ортогональны
к направлению
ортогональны
к направлению
 и друг к другу.
и друг к другу.
2. Связь характеристик распространения с параметрами среды
Установим связь между р и k. Из (1.8) получим

 (2.1)
(2.1)
Если задана периодичность в пространстве, т. е. k, то р можно найти из уравнения (2.1)

Тогда
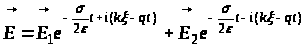
где

Распространение возможно, если q действительно. Волновой процесс, в котором поверхности равных амплитуд и поверхности равных фаз являются плоскостями, называется плоской волной. Простейшим случаем плоской волны является плоская однородная волна. В плоской однородной волне плоскости равных амплитуд совпадают с плоскостями равных фаз. Фазовая скорость такой волны будет равна

Если
 ,
то q
— мнимое, и распространения нет:
существует
,
то q
— мнимое, и распространения нет:
существует
пространственная периодичность по и монотонное затухание. Начальная форма волны не смещается вдоль оси , волновое явление вырождается в диффузию.
Частный случай временной зависимости р = i. Тогда

 (2.2)
(2.2)
Таким образом, при
 волновое число k
комплексно. Обозначим k=+i,
где
— фазовая константа,
— коэффициент затухания. Тогда
волновое число k
комплексно. Обозначим k=+i,
где
— фазовая константа,
— коэффициент затухания. Тогда


 (2.3)
(2.3)
Следовательно, при р=i
имеет место волновой процесс с затуханием,
если
 .
.
Исследуем фазовую скорость волны в среде с конечными и . Поскольку волновое число комплексно: k=+i, имеем

( >2
>считаем равным нулю).
>2
>считаем равным нулю).
В общем случае
 >1>
также комплексно:
>1>
также комплексно:
 ,
,

где , ,
 ,
— действительные
числа. Отсюда получаем выражение фазовой
скорости
,
— действительные
числа. Отсюда получаем выражение фазовой
скорости

Действительно, так как
 представляет скорость, с которой
движется плоскость постоянной фазы
представляет скорость, с которой
движется плоскость постоянной фазы
 =const
=const
то

откуда

Для определения степени затухания и фазовой скорости нужно вычислить и . Из уравнений (2.3) получаем


Введем обозначение

тогда

или

Здесь нужно оставить знак +, так как — действительное число
 (2.4)
(2.4)
Аналогично получим для
 (2.5)
(2.5)
Отсюда находим фазовую скорость
 (2.6)
(2.6)
Зависимость фазовой скорости от частоты сложная: если , , не зависят от частоты, то с увеличением фазовая скорость увеличивается, т. е. в сложной волне гармоники убегают вперед.
Рассмотрим зависимость
поглощения ,
определяемого равенством (2.5), от
электрических характеристик среды.
Член
 представляет отношение
представляет отношение
 ,
так как
,
так как
 .
Следовательно,
.
Следовательно,

Но
 ,
поэтому при tg<<1
,
поэтому при tg<<1


Ограничившись двумя членами разложения, получим
 (2.7)
(2.7)
Следовательно, по поглощению волны можно определить tg:



при
 (единица
длины) получаем
(единица
длины) получаем
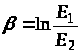
Измеряется в неперах

или в децибелах

где P — мощность.
В случае малых tg зависимость от частоты пренебрежимо мала, так как
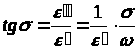

В случае tg>> 1 формулы (2.4), (2.5) можно упростить и привести к виду

Фазовая скорость

3. Вычисление затухания в данной среде
Электромагнитная волна =10м проникает в воду пресного водоема (=80, =10-3См/м) на глубину 0,5м.


 ,
tg<<1
,
tg<<1


 1/м
1/м
 ,
на глубине 0,5 м
,
на глубине 0,5 м
Список использованной литературы
Семенов А.А. Теория электромагнитных волн.-М.: Изд-во МГУ,1968.
Вайнштейн Л.А. Электромагнитные волны.-М.:Сов.Радио, 1957.
Баскаков С.И. Электродинамика и распространение волн.-М.: Высш.шк., 1992.
Бреховских Л.М. Волны в слоистых средах.-М.: Наука ,1973.
Тамм И.Е. Основы теории электричества.-М.: Наука, 1989.