Теоретические основы алгоритмизации процесса обучения младших школьников

Теоретические основы алгоритмизации процесса обучения младших школьников

Введение

Важнейшей задачей педагогической науки является совершенствование планирования процесса обучения в целом и повышение эффективности управления познавательной деятельностью учащихся.

Поиски оптимальных путей управления обучением вылились в создание новой системы учебной работы, названной программированным обучением, одной из составляющих которого является алгоритмизация.

В настоящее время наука и техника развиваются настолько быстро, что своевременное обобщение потока научной информации без применения кибернетических средств представляет значительную трудность.

Не менее сложным является сообщение учащимся знаний, так как их объем из года в год увеличивается, тогда как сроки и методы обучения остаются неизменными. В связи с этим все большее число преподавателей приходит к выводу о недостаточности традиционных способов обучения и необходимости их совершенствования на основе новейших достижений науки и техники.

В школах уже появились компьютеры, но этого недостаточно. Самый лучший вариант оснастить подобным оборудованием каждый кабинет и включить элементы работы на компьютере в учебные программы по всем предметам. Но для этого необходима техническая база. В настоящее время в начальных классах возможно использовать только элементы программированного и алгоритмизированного обучения. Поэтому тема данной работы является актуальной сегодня.

Разработкой программирования и алгоритмизации в обучении занимались такие ученые, как П. Я. Гальперин, Л. Н. Ланда, Н. Ф. Талызина. В своих работах и исследованиях они доказывали эффективность программированного обучения и алгоритмизации.

Цель курсовой работы – теоретическое обоснование необходимости алгоритмизации процесса обучения младших школьников.

В соответствии с целью определены следующие задачи:

- определить сущность понятия «программированное обучение» и «алгоритмизация»;

- выявить основные виды алгоритмов;

- определить особенности работы с различными видами алгоритмов.

Глава 1. Теоретические основы алгоритмизации процесса обучения младших школьников

1.1. Сущность программированного обучения

В психолого-педагогических исследованиях обычное, или традиционное обучение считается плохо управляемым. По мнению большинства отечественных ученых и педагогов, основными недостатками традиционного обучения выступают следующие:

1. Усредненный общий темп изучения материала.

2. Единый усредненный объем знаний, усваиваемых учащимися.

3. Непомерно большой удельный вес знаний, получаемых учащимися в готовом виде через учителя без опоры на самостоятельную работу по приобретению этих знаний.

4. Почти полное незнание учителем хода усвоения учащимися сообщаемых знаний (нет внутренней обратной связи и слабая внешняя обратная связь).

5. Недостаточное стимулирование познавательной активности учащихся, опора в основном на учителя.

6. Преобладание словесных методов изложения знания, создающих объективные предпосылки рассеивания внимания.

7. Затрудненность самостоятельной работы учащихся с учебником из-за недостаточной расчлененности учебного материала, сухости языка, почти полного отсутствия эмоционального воздействия.

Возникновение программированного обучения связано с попыткой устранить эти и другие недостатки обычного обучения.

Программированное обучение – это система последовательных действий (операций), выполнение которых ведет к заранее запланированному результату.[6,37].

Значительную роль в формировании программированного обучения сыграл известный психолог Б.Ф.Скиннер, который в 1954 г. призвал педагогическую общественность повысить эффективность преподавания за счет управления процессом обучения, построения его в полном соответствии с психологическими знаниями о нем.

Основным постулатом теории Б.Ф.Скиннера служит тезис о том, что результат предшествующего действия (вернее — его психологический эффект) влияет на последующее поведение [6,87]. Следовательно, самим поведением можно управлять путем подбора определенных вознаграждений (подкреплений) верных действий, стимулируя, таким образом, дальнейшее поведение в ожидаемом русле.

В качестве центрального понятия для построения программированного обучения выступает категория управления. Как отмечает Н.Ф.Талызина, «истинная проблема заключается в том, чтобы на всех ступенях образования обучение было с хорошим управлением, включая и начальную школу и даже дошкольные учреждения» [8, с. 54].

Б.Ф.Скиннер и его последователи выявили законы, по которым формируется поведение, и на их основе сформулировали законы научения:

1. Закон эффекта подкрепления: если связь между стимулом и реакцией сопровождается состоянием удовлетворения, то прочность связей нарастает, и наоборот. Отсюда вывод: в процессе обучения нужно больше положительных эмоций.

2. Закон упражнений: чем чаще проявляется связь между стимулом и реакцией, тем она прочнее (все данные получены экспериментальным путем).

3. Закон готовности: на каждой связи между стимулом и реакцией лежит отпечаток нервной системы в ее индивидуальном, специфическом состоянии.[6,45].

В основу технологии программированного обучения Б. Ф. Скиннер положил два требования:

1) уйти от контроля и перейти к самоконтролю;

2) перевести педагогическую систему на самообучение учащихся.

В основе концепции программированного обучения лежат общие и частные дидактические принципы последовательности, доступности, систематичности, самостоятельности. Эти принципы реализуются в ходе выполнения главного элемента программированного обучения — обучающей программы, представляющей собой упорядоченную последовательность задач. Для программированного обучения существенно наличие «дидактической машины» (или программированного учебника). В этом обучении в определенной мере реализуется индивидуальный подход как учет характера освоения обучающимся программы. Однако главным остается то, что процесс усвоения, выработки умения управляется программой.

Программированное обучение в конце 60-х — начале 70-х гг. получило новое развитие в работах Л.Н. Ланды, который предложил алгоритмизировать этот процесс.

Алгоритм есть правило (обратное утверждение неправомерно), предписывающее последовательность элементарных действий (операций), которые в силу их простоты однозначно понимаются, исполняются всеми; это система указаний (предписаний) об этих действиях, о том, какие из них и как надо производить Алгоритмический процесс — это система действий (операции с объектом, он есть не что иное, как последовательное и упорядоченное выделение в том или ином объекте определенных его элементов. Одним из преимуществ алгоритмизации обучения является возможность формализации и модельного представлении этого процесса.

Преимущества управления, программирования в образовательном процессе наиболее полно и теоретически обоснованно представлены в обучении, основанном на психологической теорю поэтапного формирования умственных действий П. Я. Гальперина.[4,65].

В теории П. Я. Гальперина процесс формирования умственные действий проходит 5 этапов:

1. Предварительное ознакомление с действием, с условиями его выполнения.

2. Формирование действия в материальном виде с развертыванием всех входящих в него операций.

3. Формирование действия во внешней речи.

4. Формирование действия во внутренней речи.

5. Переход действия в глубокие свернутые процессы мышления[4,76].

Совместно с Н.Ф.Талызиной П.Я.Гальперин реализовал эту теорию на практике в процессе обучения. Исходными теоретическими постулатами послужили следующие положения, разработанные в отечественной психологии Л. С. Выготским, С. Л. Рубинштейном, А.Н.Леонтьевым:

— всякое внутреннее психическое есть превращенное, интерио-ризированное внешнее; сначала психическая функция выступает как интерпсихическая, затем как интрапсихическая;

— психика (сознание) и деятельность суть единство, а не тождество: психическое формируется в деятельности, деятельность регулируется психическим (образом, мыслью, планом);

— психическая, внутренняя деятельность имеет ту же структуру, что и внешняя, предметная;

— психическое развитие имеет социальную природу: развитие человеческих индивидов пошло не путем развертывания внутреннего, наследственно заложенного видовым опытом, а путем усвоения внешнего общественного опыта, закрепленного в средствах производства, в языке;

— деятельностная природа психического образа позволяет рассматривать в качестве его единицы действие. Отсюда следует, что и управлять формированием образов можно только через посредство тех действий, с помощью которых они формируются[4,65].

П. Я. Гальперин поставил перед обучением принципиально новые задачи: описать любое формируемое действие совокупностью его свойств, подлежащих формированию; создать условия для формирования этих свойств; разработать систему ориентиров, необходимых и достаточных для управления правильностью формирования действия и избегания ошибок. П.Я.Гальперин разграничил две части осваиваемого предметного действия: его понимание и умение выполнить. Первая часть играет роль ориентировки и названа ориентировочной, вторая — исполнительной. П.Я.Гальперин придавал особое значение ориентировочной части, считая ее и «управляющей инстанцией»; позднее он назовет ее «штурманской картой».[4,123]

В результате проведенных П.Я.Гальпериным и его учениками исследований было установлено, что:

а) вместе с действиями формируются чувственные образы и понятия о предметах этих действий. Формирование действий, образов и понятий составляет разные стороны одного и того же процесса. Более того, схемы действий и схемы предметов могут в значительной мере замещать друг друга в том смысле, что известные свойства предмета начинают обозначать определенные способы действия, а за каждым звеном действия предполагаются определенные свойства его предмета;

б) умственный план составляет только один из идеальных планов. Другим является план восприятия. Возможно, что третьим самостоятельным планом деятельности отдельного человека является план речи. Во всяком случае, умственный план образуется только на основе речевой формы действия;

в) действие переносится в идеальный план или целиком, или только в своей ориентировочной части. В этом последнем случае исполнительная часть действия остается в материальном плане и, меняясь вместе с ориентировочной частью, в конечном счете превращается в двигательный навык;

г) перенос действия в идеальный, в частности умственный, план совершается путем отражения его предметного содержания средствами каждого из этих планов и выражается многократными последовательными изменениями формы действия;

д) перенос действия в умственный план, его интериоризация составляют только одну линию его изменений. Другие, неизбежные и не менее важные линии составляют изменения: полноты звеньев действия, меры их дифференцировки, меры овладения ими, темпа, ритма и силовых показателей. Эти изменения, во-первых, обусловливают смену способов исполнения и форм обратной связи, во-вторых, определяют достигнутые качества действия. Первые из этих изменений ведут к преобразованию идеально выполняемого действия в нечто, открываемое в самонаблюдении как психический процесс; вторые позволяют управлять формированием таких свойств действия, как гибкость, разумность, сознательность, критичность и т.д. [11,17]. Основной характеристикой выполняемых действий П.Я.Гальперин считал разумность.

Теория поэтапного формирования умственных действий явилась фундаментом разработанного Н.Ф.Талызиной нового направления — программирования учебного процесса. Его цель — определение исходного уровня познавательной деятельности обучающихся, новых формируемых познавательных действий; содержания обучения как системы умственных действий, средств, т.е. действий, направленных на усвоение широкого крута знаний по третьему типу ориентировки (в плане развернутой речи); пяти основных этапов формирования умственных действий, на каждом из которых к действиям предъявляются свои требования; разработка алгоритма (системы предписаний) действий; обратная связь и обеспечение на ее основе регуляции процесса научения.[4,124].

Существенными для реализации направления программирования обучения являются общие характеристики действий: по форме (материальное, внешнеречевое, речь «про себя», умственное);

по степени обобщенности; по мере развернутости; по мере освоения и тому, дается ли действие в готовом виде или осваивается самостоятельно.

В действии выделяются ориентировочные, исполнительные и контрольные функции. Согласно Н.Ф.Талызиной, «любое действие человека представляет собой своеобразную микросистему управления, включающую 'Управляющий орган" (ориентировочная часть действия), исполнительный, "рабочий орган" (исполнительная часть действия), следящий и сравнивающий механизм (контрольная часть действия)» [8, 66].

Центральным звеном формирования умственных действий является его ориентировочная основа, характеризуемая полнотой, обобщенностью и степенью самостоятельного освоения действий. Третий тип ориентировочной основы действий (в развернутой речи), отличаясь оптимумом полноты, обобщенности, самостоятельности, обеспечивает наивысшую эффективность формирования умственных действий.

Соотнося между собой существующие подходы к обучению, Н.Ф.Талызина отмечает, что по сравнению с бихевиористской теорией программирования теория поэтапного формирования умственных действий «строит наиболее рациональную структуру (систему познавательных действий)»; это подлинное управление развитием человека. В то же время эта теория служит примером последовательного воплощения деятельностного подхода к обучению.

В целом программированное обучение характеризуется совокупностью пяти признаков/принципов:

1) наличия поддающейся измерению цели учебной работы и алгоритма этой цели;

2) расчлененности учебной части на шаги, связанные с соответствующими дозами информации, которые обеспечивают выполнение каждого шага;

3) завершения каждого шага самопроверкой, результаты которой дают возможность судить о том, насколько он успешен, и предложения студенту достаточно эффективного средства для этой самопроверки, а если требуется, то и соответствующего корректирующего воздействия;

4) использования автоматического, полуавтоматического (матрицы, например) устройства;

5) индивидуализации обучения (в достаточных и доступных пределах).

Особая роль принадлежит созданию соответствующих программированных пособий. Программированные пособия отличаются от традиционных тем, что в последних программируется лишь учебный материал, а в программированных — не только учебный материал, но и его усвоение, и контроль за ним. При обучении очень важно вовремя отметить образование смысловых барьеров. Они возникают, когда учитель, оперируя определенными понятиями, подразумевает одно, а ученики понимают другое.

Минимизация и преодоление смысловых барьеров — одна из трудно разрешаемых проблем обучения. В этой связи дидактическое обеспечение программированного обучения обязательно включает обратную связь: внутреннюю (к обучаемому) и внешнюю (к преподавателю).

Материальной основой программированного обучения является обучающая программа, которая представляет собой специально созданное на основе пяти отмеченных выше принципов пособие. В этом пособии, как уже говорилось, программируется не только учебный материал, но и его усвоение (понимание и запоминание), а также контроль. Обучающая программа выполняет ряд функций преподавателя:

— служит источником информации;

— организует учебный процесс;

— контролирует степень усвоения материала;

— регулирует темп изучения предмета;

— дает необходимые разъяснения;

— предупреждает ошибки и т.д.[7,105].

Действие обучаемого, как правило, немедленно контролируется ответами. Если действие выполнено правильно, то обучаемому предлагается перейти к следующему шагу. При неверном действии в обучающей программе обычно разъясняются характерные ошибки, допущенные обучаемыми.

Таким образом, обучающая программа — это опосредованная материальная реализация алгоритма взаимодействия учащегося и преподавателя, которая имеет определенную структуру. Она начинается со вступительной части, в которой преподаватель непосредственно обращается к ученику, указывая цель данной программы. Кроме того, во вступительной части должна быть некая «завлекалочка», чтобы заинтересовать ученика, а также краткая инструкция по выполнению программы.[7,51].

Основная часть обучающей программы состоит из нескольких шагов. Они бывают ознакомительными, ознакомительно-тренировочными или тренировочными. Каждый шаг может включать несколько кадров, если это компьютерная программа. На одном дается краткая, поддающаяся измерению информация и затем задание или вопрос, чтобы ученик мог дать свое решение, ответить на поставленный вопрос, т.е. совершить какую-то операцию Такой кадр называется информационно-операционным. Если ученик ответил правильно, высвечивается информация, подтверждающая правильность его ответа, и дается стимул для дальнейшей работы. Если ученик ответил неточно или неверно, появляется кадр с наводящими вопросами или разъясняющей его ошибку информацией.

Заключительная часть обучающей программы носит обобщающий характер: приведение в систему сообщенного в основной части материала, инструкция по проверке обобщенных данных (самопроверка или проверка преподавателем).

Если обучающая программа безмашинная (сейчас это уже редко практикуется, поскольку есть ЭВМ), то рекомендуется составлять методическую записку для преподавателя. Она включает спецификацию обучающей программы и рекомендации преподавателю для правильного использования обучающей программы и учета ее результатов. Спецификация — это следующие указания:

1. Назначение программы: вуз, колледж, семестр, специальность, характеристика исходного уровня продвинутости учеников (что они должны знать и уметь, чтобы выполнить данную программу).

2. Цель программы: чему и с использованием какого материала научится ученик в результате выполнения заданной программы.

3. Время, необходимое на выполнение программы.

4. Характеристика программы по степени массовости (фронтальная, индивидуально-групповая), по специфике протекания учебного процесса (ознакомительная, тренировочная, ознакомительно-тренировочная), цели (вид деятельности: устно, письменно), по месту выполнения (аудиторная, домашняя, лабораторная), отношению к обучающим устройствам (машинная, безмашинная).

5. Отношение к другим обучающим программам и непрограммированным пособиям (т.е. что было до нее и что будет после нее).[7,97].

Особенностью этого вида обучения заключается в том, что ученик работает самостоятельно в посильном режиме и результат заданий фиксируется, при этом осуществляется индивидуальный подход к каждому ученику.

1.2. Алгоритмизация обучения

Среди психологических исследований, направленных на совершенствование учебного процесса, важное место принадлежит разработке способов алгоритмизации обучения.Всякий мыслительный процесс состоит из ряда умственных операций. Чаще всего многие из них не осознаются, а иногда о них просто не подозревают. Психологи подчеркивают, что для эффективного обучения эти операции надо выявить и специально им обучать. Это не менее необходимо, чем обучение самим правилам. Без овладения операционной стороной мышления знание правил сплошь и рядом оказывается бесполезным, ибо ученик не в состоянии их применить. В данном случае выполнение умственных действий аналогично выполнению действий трудовых. В самом деле, выполнить ту или иную трудовую задачу, например сделать деталь, невозможно, не производя тех или иных трудовых операций. Точно так же нельзя решить грамматическую, математическую, физическую, вообще любую интеллектуальную задачу, не совершив ряда интеллектуальных операций. Если бы это было не так, если бы, например, для грамотного письма достаточно было одного знания правил, то в школе не было бы неуспевающих по русскому языку.(6,37).

Под алгоритмом обычно понимают точное, общепонятное описание определенной последовательности интеллектуальных операций, необходимых и достаточных для решения любой из задач, принадлежащих к некоторому классу.[5,63].

Психологи исследуют несколько видов алгоритмов. Основное внимание было обращено на исследование алгоритмов распознавания (т. е. таких алгоритмов, которые предписывают, что и как надо делать, чтобы распознать, к какому классу принадлежит данный объект). Это вполне естественно, если учесть роль процесса распознавания в школьной практике. В самом деле, любые преобразования, которые должен осуществлять ученик, включают в себя в качестве компонента, а часто и специальной задачи распознавание принадлежности определенному классу. Специальное обучение процессам распознавания и выяснение возможностей их алгоритмизации становятся поэтому важной задачей обучения.[10,27].

Насколько это актуально, говорит, например, анализ ошибок, возникающих при решении грамматической задачи.

Грамматическая ошибка—показатель неумения решить грамматическую задачу. Исследование показывает, что учащиеся, которые хорошо помнят все правила, делают ошибки именно потому, что не знают, как эти правила применять, не знают соответствующих методов действий и рассуждений. Не зная общих методов решения грамматических задач, учащиеся не могут дать полного ответа на вопрос, что и в какой последовательности надо делать, чтобы распознать данное грамматическое явление (например, является ли данноепредложение сложносочиненным или сложноподчиненным).Психологи отмечают большую разнородность приемов решения одной и той же задачи разными учащимися. Было замечено также, что, разбирая какое-либо предложение, ученик идет одним путем, разбирая следующее, аналогичное,— другим, хотя самом деле метод действия в обоих случаях должен быть общим, единым. В связи с этим у учащихся часто возникает неуверенность в своих действиях и решениях.Часто ошибки возникают оттого, что учащиеся знают и применяют лишь часть операций, необходимых для распознавания того или иного грамматического явления, или пользуются ими не в той последовательности, в которой необходимо.[3,34].

Обучение алгоритмам можно производить по-разному. Можно, например, давать учащимся алгоритмы в готовом виде, чтобы они могли их просто заучивать, а затем закреплять во время упражнений. Но можно и так организовать учебный процесс, чтобы алгоритмы «открывались» самими учащимися. Этот способ, наиболее ценный в дидактическом отношении, требует, однако, больших затрат времени. Сначала учебные алгоритмы разрабатывались главным разом на материале грамматики русского языка, затем в «орбиту» алгоритмического подхода стали включаться другие учебные предметы.

Составив алгоритмы анализа (распознавания), скажем, синтаксических явлений, ученые начали обучать им учащихся так же, как алгоритмам деления или умножения в арифметике. При этом применение алгоритма к решению синтаксической задачи с такой же необходимостью должно было приводить к определению правильной пунктуации, с какой применение алгоритма деления двух чисел приводит к получению правильного частного. Обучающий эксперимент начинался с так называемого «логического урока», во время которого на простых примерах школьников подводили к пониманию отношений, лежащих в основе распознавания тех или иных синтаксических явлений. Затем усвоение этих отношений закреплялось в ходе алгоритмизованного разбора конкретного синтаксического явления.[16,19].

В целях оперативного контроля за усвоением алгоритма ученые предложили ввести особым образом составленные тетради для самостоятельных работ. Для этих тетрадей были разработаны специальные типы заданий-упражнений. Их специфика состоит в том, что, выполняя такие задания, ученик должен расчленить процесс решения на отдельные операции, а затем с необходимостью все их производить, ясно и четко осознавая каждую из них. Ученик не может уклониться от выполнения необходимой работы, поскольку он должен фиксировать в тетради результаты каждой операции (все они строго пронумерованы и расположены в определенном порядке).

Благодаря ведению таких тетрадей учитель имеет возможность значительную часть работы по контролю осуществлять прямо на уроке, в то время, когда учащиеся выполняют задание. Результаты эксперимента оказались достаточно убедительны.[14,64].

Не оспаривая эффективность такого способа обучения, его оппоненты выдвигают все же ряд возражений. Высказывается опасение, что обучение алгоритмам может привести к стандартизации мышления, к подавлению творческих сил детей. Но, отвечают сторонники алгоритмизации, надо воспитывать не только творческое мышление. Огромное место в обучении занимает выработка различных автоматизированных действий — навыков. Эти навыки — необходимый компонент творческого процесса, без них он просто невозможен. Далее, обучение алгоритмам не сводится к заучиванию их. Оно предполагает и самостоятельное открытие, построение и формирование алгоритмов, а это есть творческий процесс. Таким образом, алгоритмизация может быть прекрасным средством обучения творческому мышлению. Наконец, алгоритмизация охватывает далеко не весь учебный процесс, а лишь те его компоненты, где она представляется целесообразной.

Неверно представлять дело и так, будто алгоритмизация, автоматизируя некоторые стороны учебной деятельности, в какой-то мере умаляет роль учителя. Учитель, по убеждению сторонников этого способа обучения, был и останется главной фигурой в обучении. На нем по-прежнему будут лежать функции организации коллектива и воспитания учеников. Влияние его личности не сможет заменить никакое алгоритмизованное пособие или обучающая машина. Неосновательно и мнение, что алгоритмы представляют собой некоторый сверхпрограммный материал, осложняющий учебный процесс. Дополнительная нагрузка и трудности для учащихся создаются не тогда, когда в их умственную деятельность вносится определенный порядок и система, а когда эти порядок и система отсутствуют.

1.3. Алгоритм и его основные виды.

Алгоритм — одно из важнейших понятии информатики. Алгоритм —точное, однозначно понимаемое предписание о выполнении в указанной последовательности операций (действии), приводящих к решению любой из задач, принадлежащих к некоторому классу (или типу). Предписываемые операции (действия) должны быть доступны адресату. Они могут быть как элементарными (простейшими), так и сложными, основанными на элементарных. К алгоритмам предъявляются требования:

однозначности предписываемых действий и операций;

результативности, предполагающей, что при выполнении конечного числа операций будет получен искомый результат;

массовости, означающей, что алгоритм применим к решению целого класса задач. [6,39]

В процессе решения задачи по алгоритму должны присутствовать: само предписание, состоящее из указаний (команд) о выполнении действий или операций над определёнными объектами и обычно фиксированное (в виде схем, слов, знаков) на тех или иных материальных носителях; система-исполнитель (человек или машина), к которой эти указания адресованы и которая их выполняет; объекты, на которые направлены действия или операции которые под их воздействием преобразуются.

Примером алгоритма может служить известный способ сложения двух чисел «столбиком». Этот алгоритм можно представить в виде системы указаний: выделить в слагаемых разряды единиц и сложить единицы, если полученная сумма меньше 10, записать её в разряде единиц под нижним числом, если сумма больше или равна 10, записать в разряде единиц только кол-во единиц; выделить в слагаемых разряд десятков и записать полученный при сложении единиц десяток над разрядом десятков 1-го (верхнего) слагаемого; сложить десятки и т. д. Аналогичные указания даются для сложения единиц других разрядов числа. Системой-исполнителем данного алгоритма может быть как ЭВМ, так и человек.

В теорию и практику обучения понятие алгоритма вошло в кон. 50-х гг. в связи с развитием программированного обучения и применением обучающих машин.

Участие человека в учебном процессе накладывает ряд ограничений на использование алгоритмов. При создании алгоритма для ЭВМ составителю алгоритма точно известен набор доступных ей операций. Возможности человека определяются его предыдущим приобретённым опытом, творческими данными и др. индивидуальными факторами, которые полностью учесть практически невозможно. Поэтому при разработке алгоритмов для человека требования конструктивности и результативности алгоритмов выполняются с известным приближением. Алгоритмы, предназначенные для использования их человеком, иногда называют предписаниями алгоритмического типа, а чаще — просто предписаниями. Возможность решения задач с помощью таких предписаний носит вероятностный характер и зависит от целого ряда индивидуальных особенностей исполнителя (его интеллектуального уровня, внимания, эмоционального состояния и др.)

Алгоритм - такое предписание, которое определяет содержание и последовательность операций, превращающих исходные данные в искомый результат [9,16].

Согласно теории В.П.Беспалько, основными свойствами алгоритма являются:

1 .Определенность (простота и однозначность операций).

2.Массовость (приложимость к целому классу задач).

3.Результативность (обязательное подведение к ответу).

4.Дискретность (членение на элементарные шаги)"[7,15].

Не следует алгоритм обучения путать с машинными алгоритмами - в них логические операции должны быть предельно элементарными;

- шаги алгоритма обучения строятся с учетом фактического уровня развития учащихся и их предшествующей подготовки;

- в алгоритмах обучения последовательность операций иногда определяется не логико-грамматическими или логико-математическими, а чисто дидактическими принципами;

- алгоритм обучения допускает большую свободу в характере использования его учащимися (его предписания могут применяться по-разному).

В этом состоит отличие алгоритмов обучения от машинных алгоритмов

Таким образом, алгоритмом обучения называют такое логическое построение, которое вскрывает содержание и структуру мыслительной деятельности ученика при решении задач данного типа и служит практическим руководством для выработки навыков или формирования понятий.

В процессе обучения существуют такие разновидности алгоритмов:

- алгоритмы поиска, которые обеспечивают правильное вычленение признаков и безошибочное, быстрое выявление в тексте тех мест, где надо применять один из разрешающих алгоритмов;

- разрешающие алгоритмы, служащие разграничению сходных написаний, категорий и форм.

Разрешающие алгоритмы строятся по принципу задач с одним или несколькими альтернативными вопросами. Алгоритмы разрешения разнородны по объему: от 3-4 шагов до 30-40 и более.

Алгоритм с широким охватом правил можно назвать обобщающими. Они обобщают серию однородных правил. Основное преимущество обобщающих алгоритмов состоит в том, что они помогают с самого начала изучения материала формировать правильные и полные обобщения, учат школьников тому, как наиболее экономно и правильно находить ответ при решении учебно-познавательных задач. Эффективность использования обобщающих алгоритмов в значительной степени определяется их простотой и доступностью, уровнем сходства всех способов описания моделей в общей цепочке: правило - алгоритм - схема устного рассуждения образцы устного рассуждения, графическая фиксация умственных действий. Все эти действия оказывают эффективное воздействие лишь в комплексе, поэтому "опора только на образцы обоснования правил или только на схемы алгоритмических предписаний заметно снижает эффективность обучения рациональным приемам применения знаний.[12,27].

В существующей практике обучения орфографии наиболее часто применяются модели ДИХОТОМИЧЕСКОГО АЛГОРИТМА - в форме дерева признаков с альтернативными ответами: "да" - "нет". Используя дихотомические алгоритмы, ученик мысленно продвигается сверху вниз, постепенно осуществляя операции выбора из двух возможных вариантов: "да" или "нет", и таким образом приходит к правильному выводу. Реже используются модели политомических алгоритмов, которые выполняют функции как распознающих, так и разрешающих предписаний. Эти модели очень полезны при формировании умений и навыков.

При обучении политомическая модель предписания облегчает работу учащихся на этапе применения знаний, однако не устраняет многих затруднений, с которыми они сталкиваются в процессе работы с дихотомическими алгоритмами.

Опыт применения описанных Е.Т.Шатовой моделей предписаний показал, что политомический алгоритм более нагляднее и компактнее, лучше просматривается и запоминается.[10,10].

Но по-нашему мнению, в начальных классах предпочтительней другие виды алгоритмов, так как младшие школьники не в состоянии охватить общую картину, обозначенную в политомическом алгоритме. Им легче проследить логику работы по правилу с помощью дихотомического предписания.

Там, где возможно, предписания дихотомического и политомического типов заменяют моделями типа алгоритм-формула. Алгоритм-формула представляет собой определенную систему знаков (букв, цифр, кратких графических обозначений), отражающих структуру и содержание как орфографических правил, так и приемов и образцов их применения. Именно такая модель оказалась более эффективной.

Покажем на конкретном примере один из вариантов методики построения и ввода алгоритма - формулы применительно к теме "Буквы Е и И в падежных окончаниях существительных". Вначале учащимся предлагается "чистая" таблица, которая заполняется под руководством учителя в процессе эвристической беседы и в итоге приобретает следующий вид:

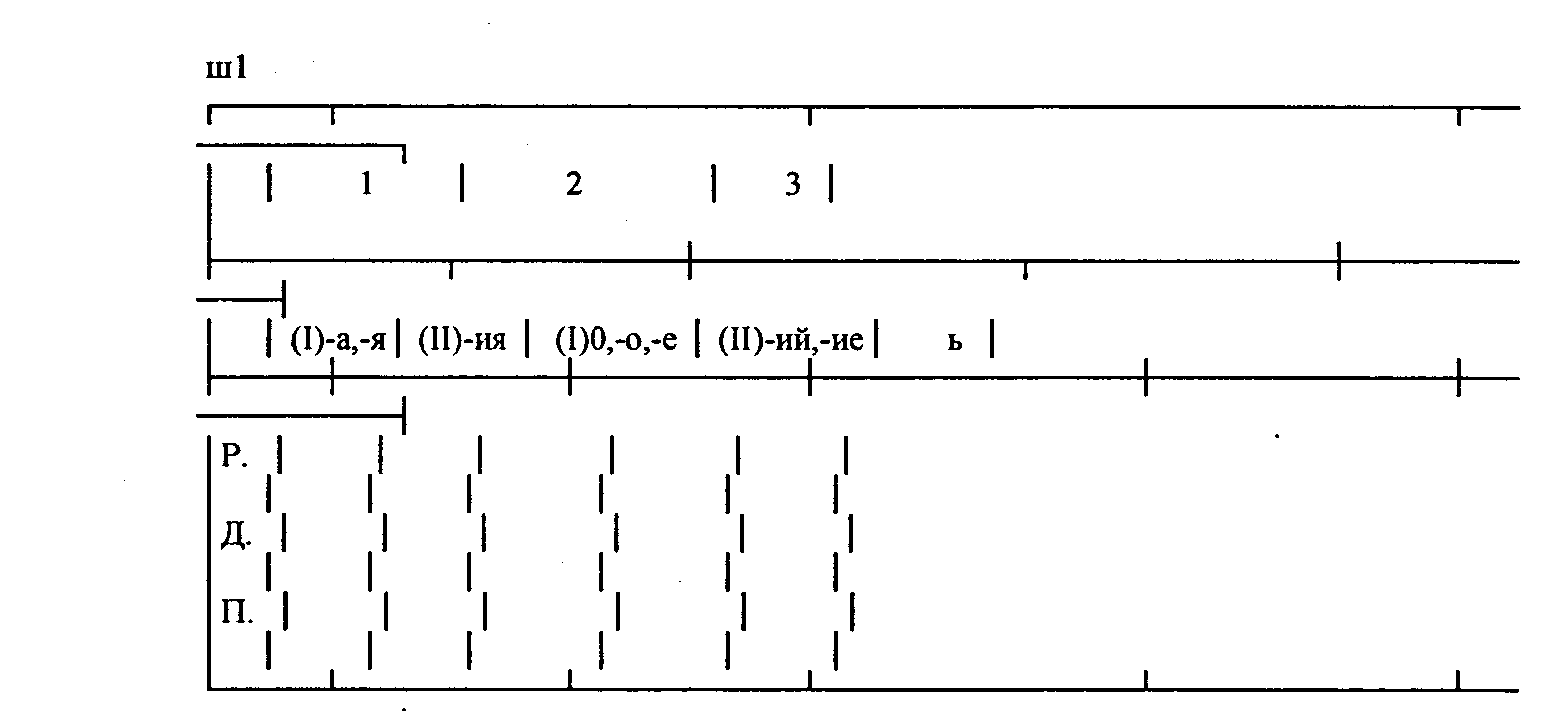
В результате совместной работы учителя и учащихся вначале вводится формула обобщенного правила правописания буквы Е (условное название - правило-формула). Ход мыслей при построении, а затем и при чтении формулы данного правила для учащихся предельно ясен: опираясь на таблицу, они продвигаются сверху вниз - от склонения (первый ярус) к группе (второй ярус) и затем к падежам и окончаниям.

Форма суждения должна ориентировать учащихся на выполнение умственных действий по принципу: "Вначале объясни ("если то-то..."), а затем запиши ("пишу так-то...")", что очень важно для формирования мотивированных обобщений на этапе первичного обучения материала.

Учебная задача - это цель познавательной деятельности; она всегда содержит вопрос (определяющая часть задачи), условия выполнения, порядок выполнения (план решения или алгоритм) и результат решения - ответ. Метод решения грамматике - орфографических задач применяется ко всем проверяемым орфограммам, но типы задач и порядок их решения различны. Рассмотрим составные элементы задачи и ее решение на примере.

Вопрос, то есть осознание цели того, что должно быть получено. Для проверки слова "весы" [в'исы] задача - это выяснение, какую букву надо написать после "в" для обозначения гласного звука.

Условия: отсутствие ударения (безударный гласный в корне слова). Важно подчеркнуть положение безударного гласного звука - он стоит в корне слова : "вес-".

Порядок выполнения (алгоритм): выделение безударного гласного - определение его места в морфеме (в данном случае - в корне) - подбор проверочного слова с проверяемым гласным. В данном примере проверочное слово - "вес".

Вывод: проверка подтвердила, что в корне слова "вeсы" следует писать букву "е": "весы".

М. Р. Львов, М. Разумовская указывают, что: "Решая орфографическую задачу, школьник должен совершить следующие действия:

во-первых, увидеть орфограмму в слове, словосочетании, тексте;

во-вторых, определить ее вид: проверяемая или нет; если да, то к какой грамматике - орфографической теме относится; вспомнить правило;

в-третьих, определить способ решения задачи в зависимости от типа орфограммы, от соответствующего правила;

в-четвертых, определить "шаги", ступени решения и их последовательность, то есть составить (обычно восстановить в памяти) алгоритм решения задачи;

в-пятых, решить задачу, то есть выполнить последовательные действия по алгоритму, не пропустив ни одного и не совершив ошибки ни на одной из ступеней; получить результат - вывод о правильности написания;

в-шестых, написать слово в соответствии с решением задачи и осуществить самопроверку.[4, 21]

Такова в общих чертах структура действий учащегося, проверяющего орфограмму с помощью правил методом решения задачи. Действия очень сложны для 8-9- летнего ребенка. Как правило, несоблюдение указанного порядка приводит к ошибкам.

Несколько иной порядок действий описан Н.Н. Алгазиной:

1) ученик должен обнаружить орфограмму (опознавательный этап анализа);

2) установить, какое орфографическое правило необходимо применить в данном случае (выборочный этап анализа);

3) решить вопрос о конкретном написании, выделив существенные признаки, необходимые и достаточные для применения орфографического правила (заключительный этап анализа)"[2,34].

Идеи моделирования и алгоритмизации умственной деятельности учащихся все более проникают в школьную практику. В помощь учащимся создаются памятки, указания в виде плаката-инструкции, где даны 3-4 рекомендации в нужной последовательности.

Обучение использованию алгоритмов проходит в 3 этапа.

1 .Подготовительный этап - подготовка базы для работы с новым материалом , актуализация навыков, на которых основано применение алгоритма, формирование нового навыка. Учащиеся должны быть подготовлены к выполнению всех элементарных операций алгоритма.

Время, отведенное на эту работу, зависит от уровня подготовленности учащихся.

Без этого этапа упражнения по алгоритму могут привести к закреплению ошибок.

2.Основной этап:

а) начинается с момента объяснения правила. Класс должен активно участвовать в составлении и записи алгоритма. Учитель проводит бесед)', в результате которой на доске появляется запись алгоритма. Она облегчает понимание и усвоение алгоритма.

б) далее по схеме разбираются 2-3 примера.

в) раздаются карточки с алгоритмами или работа ведется по общей таблице.

Содержание перечитывается одним учеником. Затем выполняются тренировочные упражнения (сначала - коллективно, затем - самостоятельно). Необходима жесткая фиксация умственных действий (например, в форме таблицы).

г) развернутое комментирование (карточки закрываются)

д) дети стараются не использовать карточки и комментарии (но при необходимости пользуются).

Тренировочный материал на этом этапе: упражнения учебника, специально подобранные слова и тексты, запись под диктовку и самостоятельно из учебника (словосочетания, предложения или выборочные слова).

З.Этап сокращения операций.

На этом этапе происходит процесс автоматизации навыка: некоторые операции совершаются параллельно, некоторые - интуитивным путем, без напряжения памяти. Процесс свертывания происходит неодновременно и разными путями у разных учащихся.

Своевременному свертыванию алгоритма способствуют сокращенные комментарии и образцы. Комментарии эффективны тогда, когда скрывают в себе стройную логическую систему, когда они связаны между собой общими признаками и имеют определенную последовательность.

Проблемы работы с обобщающими алгоритмами примерно те же.

Для улучшения усвоения модели алгоритма существуют специальные приемы:

1) выполнить дома упражнения по алгоритму и постараться запомнить последовательность операций;

2) письмо с использованием алгоритма без схемы, одному из учащихся можно предложить задавать альтернативные вопросы, а другому - отвечать на них;

3) вопросы учащихся типа: "что будем писать при двух ответах "да", при четырех "нет"?

Вспомогательный алгоритм не требует особых приемов работы. Они просты и усваиваются без наглядных схем и карточек. Например, на уроках русского языка строятся они на основе анализа грамматическою значения и грамматических форм слова. Сначала идет различение слов по значению (предмет: кто? что?). Одновременно - практические навыки в определении грамматических форм: число (один-много), лицо (я-ты-он) и т.д. Потом алгоритм на определение частей речи:

1) Установи связь слов.

2) Что обозначает слово?

3) Что обозначает его окончание (суффикс)?

4) Как изменяется слово?

5) На какие вопросы оно отвечает?

Система работы по алгоритмам предполагает прежде всего овладение алгоритмами поиска. Существуют алгоритмы курса. Которые охватывают все изученные правила орфографии, указывают на главные типы орфограмм и обязывают учащихся к всесторонней проверке текста. Каждый пункт этого алгоритма развертывается в самостоятельный алгоритм поиска, те, в свою очередь, иногда тоже распадаются на алгоритмы поиска.

При использовании такого алгоритма могут быть следующие упражнения:

1) направленный, или выборочный, орфографический разбор с различными задачами:

- обозначить соответствующими цифрами все орфограммы прямо под строчками;

- обозначить орфограммы выборочно ( например, лишь с цифрами 3,4,5 );

- комментированное письмо с одновременным обозначением цифрами соответствующих орфограмм;

- упражнение с записью слов по рубрикам или строчкам, соответствующим пунктам этого алгоритма.

Важно, чтобы в составлении алгоритма участвовал весь класс, чтобы дети запомнили построенную модель применения правила.

"Обучаясь письму таким образом, ученик каждое слово анализирует фонетически и по составу. Это приучает его замечать все виды орфограмм, обнаруживать, где надо писать, как слышишь, где проверять правилом, где зрительно или на слух вспоминать написание. Особенно полезны такие упражнения для посредственно успевающих и отстающих учеников [13.с.23].

Таблицы с успехом могут заменить более экономные графические средства:

- точки;

- стрелки;

- вопросы;

- опорные слова;

- буквенные обозначения, представленные перед контрольными словами, после них и на полях. В результате темпы работы ускоряются. Но перейти к построчной (нетабличной) форме фиксации нельзя, прежде чем учащиеся не овладеют навыками четкой мыслительной деятельности.

Выводы по главе.

1. Программированное обучение - система учебной работы с преимущественно опосредованным программным управлением познавательной деятельностью учащихся.

2. Программное обучение является качественно новой дидактической системой. Она возникает на стыке кибернетики и педагогики. Программированное обучение использует кибернетические принципы для управления педагогическим процессом.

3. Появление идей программированного обучения привело к необходимости явного выделения в содержании обучения учебных алгоритмов (их часто называют алгоритмическими предписаниями). Учебные алгоритмы служат предметом усвоения для учащихся, а часто и средством обучения, показывающим какие действия и в каком порядке должны выполнять учащиеся, чтобы усвоить знания.

4. Выявление или построние в содержаниии и процессе обучения алгоритмов и представления их в какой-либо форме пошаговой программы деятельностью учения или преподавания называется алгоритмизацией обучения. В деятельности учащихся в прцессе учения и учителей в процессе преподования можно различать два принципиально различных способа решения возникающих в этих прцессах задач: алгоритмический. Когда субъект выполняет свою деятельность в соответствии с известным ему алгоритмом, определяющим четкую последовательность элеметнатрных для данного субъекта операций по решению любой задачи из класса; эвристический, когда главная составная часть его деятельности состоит в поисках плана или метода решения данной задачи. Как правило эти два способа деятельности в обучении не различаются и осуществляются в совметном едином процессе.

5. Психологическое значение алгоритмизации обучения состоит в том, что она способствует явному различению учащимися содержательной и операциональной сторон изучаемых знаний и овладению общим способом решения широкого класса задач, а также явному выделению из процесса овладения умственными действиями ее ориентировочной основы, благодаря чему значительно повышается эффективность обучения.

Список литературы

Амонашвили Ш. А. Воспитательная и образовательная функция оценки учения школьников./Ш. А. Амошошвили - М., 1984.,с.427

Амонашвили Ш. А, Обучение. Оценка. Отметки. / Ш. А Амонашвили - М.:Знание, 1980.с. 376

Амтаниус М. Психолого-педагогические основы контроля в учебном процессе. / М Амтаниус - М.: Изд-во МГУ, 1978, с.184

Баранов С. П. Принципы обучения. - М.: Просвещение, 1981.с.354

Беспалько В. П. Слагаемые педагогической технологии. / В. П. Баранов — М.: Педагогика, 1989.

Берг А.И. Кибернетика и обучение // Природа. - 1966. - №11. – с.34

Беспалько В.П. Педагогика и прогрессивные технологии обучения. /В.П. Беспалько - М., 1995.

Беспалько В.П. Программированное обучение. Дидактические основы. / В.П. Беспалько - М-,1971.с.34.

Беспалько В.П. Элементы теории управления процессом обучения. /В.П Беспалько - М.,1971.с.132.

Болдырев Н. И.. Педагогика. / Н. И Болдырев - М.: Просвещение, 1968.с.147

Болотпина Л. Р. Педагогика. / Л. Р Болотпина - М.: Просвещение, 1987 с.261.

Воронцов А.Б. Некоторые подходы к вопросу контроля и оценки учебной деятельности учащихся // Начальная школа, 2003 - № 7.- с.25

Гальперин П.К. К теории программированного обучения. /П.К Гальперин - М.,1967.

Лайда Л. Н. Алгоритмизация в обучении. / Л. Н. Лайда - М.: Просвещение, 1966.

Молибог А.Г. Программированное обучение. / А.Г. Молибог - М., 1967.

Педагогика / Под ред. П.И.Пидкасистого. / - М.: РПА, 1996.

Пеннер Д. И. и др. О методике составления программированных заданий // Физика в школе. -1973. - № 2 –с.76.

Розенберг Н.М. Информационная культура в содержании общего образования // Советская педагогика. - 1991. — №3. – с.24.

Селевко Г. К. Современные образовательные технологии. / Г. К Селевко – М., 1998- с.256

Талызина Н.Ф. Контроль и его функции в учебном процессе - /Советская педагогика -1989. - №3. – с.5.

Талызина Н.Ф. Управление процессом усвоения знаний. / Н.Ф Талызина. - МГУ, 1975.с.97.

Талызина Н.Ф. Формирование познавательной деятельности младших школьников. / Н.Ф Талызина - М., 2002 c.348.

Для подготовки данной применялись материалы сети Интернет из общего доступа