Определение цены заемного капитала (работа 1)
Определение цены заемного капитала
Олег Лытнев
В общем случае цена капитала – это полная доходность соответствующего финансового инструмента. В реальности цена, которую платит предприятие за привлекаемый капитал, может не совпадать с величиной доходности, получаемой инвестором. С одной стороны, у покупателя капитала возникают дополнительные расходы по привлечению ресурсов (эмиссионные издержки, комиссионные брокерам и банкам и т.п.), которые увеличивают цену этих ресурсов. С другой – издержки эмитента по выплате доходов инвесторам в некоторых случаях исключаются из суммы налогооблагаемой прибыли. Поэтому фактическая цена капитала для предприятия может оказаться ниже доходности, выплачиваемой инвесторам. Рассмотрим, как учитываются эти факторы при оценке заемного капитала.
Для привлечения долгосрочного заемного капитала предприятия эмитируют облигации. Ценой такого капитала для предприятий является полная доходность облигаций с учетом дополнительных расходов эмитента по размещению своих обязательств. Иными словами, процедура определения цены заемного капитала в основном идентична методике расчета полной доходности облигаций, рассмотренной в параграфе 5.3 настоящего пособия. Различия заключаются в необходимости учета дополнительных эмиссионных издержек. Еще одна особенность оценки заемного капитала состоит в том, что предприятие-эмитент имеет право относить сумму доходов, выплачиваемых по облигациям, на себестоимость своей продукции (услуг), уменьшая тем самым базу обложения налогом на прибыль. Возникающий при этом эффект “налогового щита” снижает цену капитала для эмитента. Для количественного измерения величины данного эффекта полную доходность облигации умножают на выражение (1 – t), где t – ставка налога на прибыль.
Таким образом, определение цены заемного капитала производится в два этапа: сначала рассчитывается полная доходность облигации (с учетом расходов по эмиссии), а затем полученный результат корректируется на величину влияния эффекта налогового щита. Например, предприятие планирует разместить трехлетние купонные безотзывные облигации номиналом 5 тыс. рублей. Купонная ставка составит 20% годовых с выплатой 2 раза в год. Размещение облигаций предполагается произвести по курсу 97% от номинала, расходы на эмиссию составят 3% от фактически вырученной суммы. Все поступления от продажи облигаций предприятие получит до начала 1-го года (нулевой период); все выплаты по облигациям будут производиться в конце каждого полугодия. Прогнозный денежный поток от данной финансовой операции (в расчете на 1 облигацию) будет иметь следующий вид (табл. 6.2.1). Величина притока в 0-й период представляет собой курсовую стоимость облигации 4,85 тыс. рублей (5 * 0,97), уменьшенную на сумму расходов по эмиссии 0,15 тыс. рублей (4,85 * 0,03).
Таблица 6.2.1
Денежный поток от размещения 3-летнего облигационного займа, тыс. руб.
|
0 период |
1 год |
2 год |
3 год |
|||
|
30 июня |
31 декабря |
30 июня |
31 декабря |
30 июня |
31 декабря |
|
|
+4,7 |
-0,5 |
-0,5 |
-0,5 |
-0,5 |
-0,5 |
-5,5 |
Для нахождения полной доходности данной финансовой операции применим формулу (5.2.2):
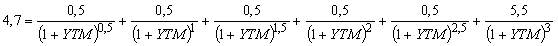
Решив полученное уравнение относительно YTM, получим полную доходность к погашению займа 24,177%. Если предприятие уплачивает налог на прибыль по ставке 30%, то цена капитала с учетом налоговой защиты (Kd) будет равна:
Kd = 0,24177 * (1 – 0,3) = 16,924%
Таким образом, предприятие сможет привлечь долгосрочный заемный капитал по цене 16,924% годовых. Вычисление YTM требует использования компьютера или специальных таблиц – книг доходности. Однако, для нахождения приближенной величины полной доходности можно воспользоваться упрощенной формулой (5.2.3). В качестве параметра CF в этом выражении указывается сумма годового купона (1 тыс. руб. в нашем примере), буквой N обозначается номинал облигации (5 тыс. руб.), а буквой P – ее продажная цена, уменьшенная на сумму расходов по размещению (4,7 тыс. руб.). Переменная n означает срок облигации (в нашем примере 3 года). Подставив эти значения в формулу (5.2.3), получим:

Расхождение в 1,5 процентных пункта (24,177 – 22,68) является довольно значительным, но оно объясняется еще и тем, что при использовании приближенной формулы не была учтена фактическая периодичность выплаты купона (2 раза в год). Если бы по условию займа купонные выплаты производились только 1 раз в год (по 1 тыс. рублей), то YTM такого денежного потока составила бы 22,982%, то есть всего на 0,3 процентных пункта больше приближенного значения полной доходности (22,982 – 22,68). После налоговой корректировки это расхождение стало бы еще меньше:
(22,982 * 0,7) – (22,68 * 0,7) = 0,21 процентных пункта.
В параграфах 3.4 и 5.3 были рассмотрены различные виды облигаций, в том числе бескупонные, вечные, отзывные, конвертируемые. В реальности существует еще более широкое разнообразие инструментов долгового финансирования. Особенности этих инструментов влияют на способы расчета цены привлекаемого заемного капитала. Например для дисконтных облигаций (облигаций с нулевым купоном) следует использовать формулу расчета сложной эффективной процентной ставки (2.2.15), для вечных облигаций – формулу (5.3.3). Чтобы не запутаться в математических выражениях, надо хорошо усвоить простое правило: цена заемного капитала – это всегда полная доходность соответствующего финансового инструмента. В большинстве случае ее можно рассчитать как IRR денежного потока, порождаемого данным инструментом. Самое важное, правильно спрогнозировать денежный поток – определить размер и очередность каждой ожидаемой выплаты. Рассчитав внутреннюю норму доходности потока, надо не забыть скорректировать ее на величину эффекта налогового щита.
Предположим, что вместо эмиссии купонной облигации, предприятие предпочтет разместить дисконтный инструмент с таким же номиналом и на аналогичный срок. Первичная продажа облигаций будет производиться по курсу 60, а через три года предприятие вернет инвесторам номинальную стоимость облигаций. Расходы по эмиссии составят те же 3% от фактической выручки. То есть, в нулевом периоде предприятие получит 2,91 тыс. рублей (5 * 0,6 * 0,97), а в конце третьего года должно будет заплатить 5 тыс. рублей. Применив формулу (2.2.15), получим:

Но этот же самый результат можно получить, рассчитав полную доходность как IRR денежного потока (+2,91; 0; 0; -5):

И в этом случае YTM = 19,773%. С учетом налоговой защиты цена капитала составит:
Kd = 0,19773 * (1 – 0,3) = 13,841%
Вообще говоря, юридическая форма обязательств, возникающих у предприятия в процессе привлечения заемного капитала, имеет для него меньшее значение, чем структура денежных потоков, обусловленных данным процессом. Поэтому с финансовой точки зрения нет принципиальных различий между, например, эмиссией облигаций и получением долгосрочного банковского кредита. И в том, и в другом случае цена привлекаемого капитала будет определяться полной доходностью операции, которая, в свою очередь, целиком и полностью зависит от структуры соответствующего денежного потока. Предположим, что банк согласен выдать предприятию трехлетний кредит в сумме 4,7 млн. рублей. В течение его срока предприятие будет каждые 6 месяцев выплачивать банку проценты в сумме 500 тыс. рублей, а по окончании срока возвратит 5 млн. 500 тыс. рублей. Возникающий в результате этой операции денежный поток абсолютно идентичен графику, представленному в табл. 6.2.1, соответственно цена данного займа составит для предприятия те же самые 16,924%. Следовательно, для определения цены капитала, получаемого в форме долгосрочных банковских кредитов, должна применяться рассмотренная выше методика.
Например, предприятие получает в банке 10 млн. рублей на 1,5 года под номинальную ставку 22% годовых с ежемесячным реинвестированием начисленных процентов. По условиям кредитного договора уплата банку начисленных процентов должна производиться ежеквартально в течение всего срока ссуды. По окончании срока предприятие должно вернуть банку основную сумму долга. Таким образом, каждые три месяца предприятие должно будет выплачивать банку по 560,15 тыс. рублей (расчеты выполнены по формуле (2.2.13) с параметрами: P = 10000 тыс. руб., n = 0,25 года (1 квартал = 1/4 или 3/12 года), m = 12, j = 22%). Последняя выплата в конце срока составит 10560,15 тыс. рублей (10000 + 560,15). Полуторагодовой период включает в себя 6 кварталов, следовательно денежный поток по данной операции будет иметь вид: (+10000; -560,15; -560,15; -560,15; -560,15; -560,15; -10560,15). YTM этого потока найдем из формулы (5.2.2):

Она составит 24,36%. Так как проценты по банковскому кредиту включаются в состав себестоимости продукции, скорректируем полученный результат на эффект налогового щита:
Kd = 0,2436 * (1 – 0,3) = 17,052%
Цена заемного капитала составит в этом случае 17,052%.
Предположим теперь, что банк согласен на получение всей суммы начисленных процентов в конце срока ссуды, то есть он не настаивает на ежеквартальной выплате процентов. Сначала рассчитаем по формуле (2.2.13) наращенную сумму кредита к концу его срока:

Тогда денежный поток будет иметь вид (+10000; -13868,17). По формуле (2.2.15) находим, что его уравнивает эффективная процентная ставка 24,36%, то есть для предприятия этот вариант абсолютно равнозначен предыдущему и периодичность выплаты начисленных процентов не оказывает влияния на цену привлекаемого капитала. Точно такой же результат будет получен, если рассчитать сложную эффективную процентную ставку, эквивалентную номинальной ставке 22% годовых. По формуле (39) в табл. (2.2.3) получаем:

Следовательно, оба варианта погашения процентов по кредиту обусловливают одну и ту же цену заемного капитала: 24,36% или 17,052% с учетом налогообложения.
Список литературы
Для подготовки данной применялись материалы сети Интернет из общего доступа