Создание начального вращения в прыжках стопорящим действием конька о лед и закручиванием тела

Создание начального вращения в прыжках стопорящим действием конька о лед и закручиванием тела

Кандидат педагогических наук, доцент В.И. Виноградова? Московский государственный технический университет "МАМИ", Москва

Самый распространенный способ создания начального вращения в прыжках в фигурном катании - закручивание тела. Это основной способ в прыжках "петля", "тулуп", "лутц" и "валлей" и вспомогательный - в прыжке "cальхов". Стопорящее же действие конька о лед для создания начального вращения в большей или меньшей степени встречается во всех прыжках. Стопорящее действие конька - основной способ создания начального вращения в прыжке "аксель", сопутствующий - в прыжках "cальхов", "петля" и вспомогательный - в прыжках "тулуп", "флип" и "лутц" [2].

Для описания двигательных действий в прыжках построим механическую модель фигуриста. Туловище фигуриста моделируем конусом с вершиной в точке его опоры о лед и основанием радиуса Rк у плеч. Естественно, что такая модель приемлема только в том случае, когда форма туловища фигуриста приближается к конической. Считаем, что перед отрывом фигуриста ото льда его руки разведены в противоположных направлениях параллельно поверхности льда и моделируются однородными стержнями. Ось x фигуриста отклонена от нормали z к поверхности льда на угол a. Предполагаем, что вес частей тела фигуриста, головы, двух рук и туловища известен. Обозначим вес этих частей тела соответственно РГ, РР и РТ. Весовые доли соответственно kГ, kР, kТ.

Предполагаем, что фигурист скользит с известной скоростью n, стопорящее действие конька о лед происходит с силой F, а группировка рук в момент отрыва фигуриста ото льда происходит мгновенно.

Для построения математической модели создания начального вращения стопорящим действием конька о лед в общем центре масс о.ц.м. фигуриста прикладывается самоуравновешенная система двух сил, линия действия которых параллельна линии действия силы F стопорящего действия конька о лед. Из полученной таким oбpaзом системы сил, эквивалентной начальной по действию на фигуриста, выделяется пара сил, которая и создает начальное вращение.

Начальную скорость w вращения фигуриста в прыжке находим, используя теорему об изменении кинетической энергии вращения:

,

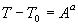где Т0 и Т - кинетическая энергия вращения фигуриста в начальный и произвольный моменты времени стопорящего действия конька о лед, Аа - работа пары сил вращения фигуриста.

Учитывая, что в начальный момент времени стопорящего действия конька о лед кинетическая энергия вращения фигуриста равна нулю (Т0=0), а в произвольный момент времени определяется выражением

, получим:

.

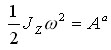(1)

Работу пары сил вращения определяем как работу силы стопорящего действия конька о лед при повороте фигуриста на угол j перед его отрывом ото льда

.

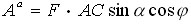Подставляя выражение для работы Аа в уравнение (1), после несложных преобразований получим формулу для определения скорости w вращения фигуриста в момент его отрыва ото льда:

.

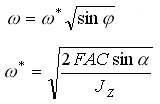(2)

Нами получено и выражение для определения силы F стопорящего действия конька о лед по экспериментальным динамическим параметрам

,

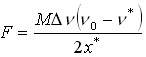(3)

где М - масса фигуриста, v=v0-v*, n0 и n* - скорости его о.ц.м. в момент начала стопорящего действия конька о лед и соответственно его отрыва ото льда, x* - длина следа стопорящего действия конька о лед.

Положение о.ц.м. фигуриста на его оси x, то есть величина АС, определяется на основании свойств системы параллельных сил веса его головы РГ, веса рук РР и веса туловища РТ.

AC = (1-kТ)LТ +kГ r,

(4)

где LТ и r - соответственно длина туловища и радиус головы.

Для принятой механической модели фигуриста определяется ее момент инерции JZ относительно нормали к поверхности льда:

JZ = JZГ + JZP + JZT;

(5)

где JZГ, JZP и JZT - моменты инерции относительно нормали z головы, рук и туловища фигуриста, которые выражаются через антропометрические параметры фигуриста.

Подставляя (3), (4) и (5) в (2), получим в аналитической форме выражение для угловой скорости вращения фигуриста перед отрывом ото льда до группировки:

.

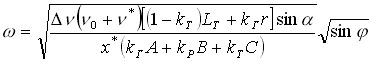(6)

В момент отрыва ото льда фигурист группируется и вращается вокруг своей оси x. Предполагается, что группировка увеличивает только массу туловища фигуриста и не изменяет его форму и объем. При этом условии находится осевой момент инерции Jx :

.

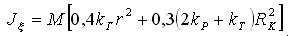(7)

В полете после группировки кинетический момент фигуриста не изменяется:

,

(8)

где 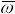- скорость вращения фигуриста в полете после группировки.

Подставляем (5), (6) и (7) в (8) и получаем многопараметрическую зависимость скорости 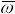вращения фигуриста в полете, которая создается стопорящим действием конька о лед:

.

Если начальное вращение создается еще и закручиванием тела фигуриста, то его кинетический момент К увеличивается:

,

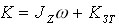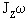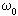где - кинетический момент фигуриста до группировки, который создается стопорящим действием конька о лед; КЗТ - кинетический момент фигуриста до группировки, который создается закручиванием тела и определяется нами [1] через скорость вращения плеч перед его отрывом ото льда:

.

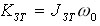Закон сохранения кинетического момента фигуриста в полете при создании начального вращения в прыжках стопорящим действием конька о лед и закручиванием тела принимает вид:

,

где 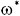- начальная скорость вращения фигуриста после группировки.

Из этого закона, опуская промежуточные математические выкладки, получаем многопараметрическое аналитическое выражение для определения скорости w* вращения фигуриста в полете, которая создается совместно стопорящим действием конька о лед и закручиванием тела:

,

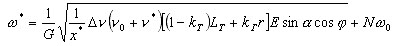где E = kГ A + kP B + kT C,

N = (0,4)kГ r2 + (8/3)kP LP2 +(0,25) kT RК2;

,

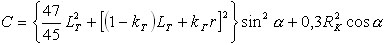Rк и Lр - соответственно радиус основания конуса и длина руки.

Наиболее существенными динамическими параметрами, как показали расчеты, которые влияют на скорость вращения фигуриста в полете и, следовательно, на многооборотность исполняемых прыжков, являются угол 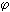поворота фигуриста, длина 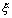* следа при стопорящем действии конька о лед, угол a отклонения фигуриста от нормали к поверхности льда, разность скоростей скольжения в моменты начала и конца стопоряще го действия конька о лед и скорость 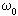вращения плеч фигуриста в момент отрыва его ото льда.

Фигурист знает, что естественное стремление к повороту на угол 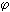= 90° при отрыве ото льда значительно усложняет технику исполнения прыжка. Однако он должен знать, что можно значительно уменьшить угол 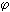, упростить исполнение прыжка и незначительно потерять в скорости вращения. Так, например, при 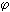= 50° потеря в скорости вращения не превышает 12%.

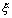Сокращение длины * следа стопорящего действия конька о лед приводит к увеличению скорости вращения в полете. Сокращение длины 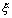* следа с 0,5 до 0,1 м может привести к увеличению скорости вращения в полете в 2 раза.

Увеличение угла a отклонения фигуриста от нормали к поверхности льда приводит к увеличению момента пары сил, которая создает начальное вращение фигуриста. Увеличение этого угла может в 3 раза увеличить скорость вращения фигуриста в полете.

Увеличение скорости 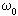вращения плеч в 4 раза позволяет увеличить скорость вращения фигуриста в полете в 2-3 раза.

Таким образом, моделирование двигательных действий фигуриста при исполнении прыжков позволяет количественно оценить влияние параметров на многооборотность прыжков и научно обоснованно ориентировать усилия тренера и фигуриста при организации тренировочного процесса.

Влияние как динамических, так и антропометри ческих параметров на увеличение многооборотности прыжков можно оценить по приведенным в статье формулам у любого конкретного фигуриста.

Список литературы

1. Виноградова В.И. Движение фигуриста при создании начального вращения в прыжках закручиванием тела //Теор. и практ. физ. культ. 1993, №1, с. 13-16.

2. Мишин А.Н. Биомеханика движений фигуриста. - М.: ФиС, 1976. - 141 с.

Для подготовки данной применялись материалы сети Интернет из общего доступа