Расчет привода швейной иглы

1

Санкт-Петербургский Государственный Институт Сервиса и Экономики

Кафедра “Технология ремонта транспортных средств”

Расчетно-пояснительная записка к

курсовому проекту по основам

конструирования и проектирования

Тема: Расчет привода иглы швейной машины

Студент: Чиркунов А.В.

Группа: 721

Специальность: 0608

Руководитель проекта: Петрова Л.Б.

Санкт-Петербург

1999 год

ОГЛАВЛЕНИЕ:

1. Расчет привода иглы швейной машины. 3

1.1. Структура привода иглы. 3

1.2. Выбор иглы. 3

1.3. Расчет иглы на прочность. 4

1.4. Выбор геометрических параметров кпм. 5

1.5. Кинематический анализ кривошипно-ползунного механизма. 6

1.5.1. Задачи анализа. 6

1.5.2. Построение плана механизма. 6

1.5.3. Построение плана скоростей. 6

1.5.4. Построение плана ускорений. 9

1.6. Расчет уравновешивающего момента. 11

1.7. Расчет мощности двигателя для привода механизма иглы. 12

2. Условия для расчетов. 13

3. Литература. 14

1. Расчет привода иглы швейной машины.

1. Структура привода иглы.

В швейных машинах для обеспечения поступательного движения иглы преду­сматривается привод, состоящий из электродвигателя, клиноременной передачи и кривошипно-ползунного механизма.

В кривошипно-ползунный механизм входят: главный вал на двух подшипниках скольжения; кривошип, соединенный пальцем с шатуном; поводок, связанный с од­ной стороны с игловодителем стопорным винтом, а с другой стороны с ползуном, перемещающимся в направляющих.

Ползун предназначен для снижения нагрузки на игловодитель от кривошипа.

Внизу игловодителя, движущегося в двух направляющих, предусмотрен игло­держатель со стопорным винтом.

Кривошипно-ползунный механизм предназначен для преобразования вращатель­ного движения в поступательное и в швейных машинах может быть исполнен в од­ном из трех вариантов. Во всех вариантах кривошип совершает вращательное движе­ние и обязательно соединен со стойкой – неподвижным звеном; ползун совершает поступательное движение, контактирует с неподвижным звеном; шатун совершает плоское или плоско-параллельное движение, являющееся комбинацией вращатель­ного и поступательного движения, со стойкой непосредственно не связан.

Основным является центральный кривошипно-ползунный механизм, у него про­должительность рабочего и холостого хода одинаковая. У смещенного механизма продолжительность рабочего хода иглы больше продолжительности холостого. Для снижения температуры иглы исполняют кривошипно-ползунный механизм с верх­ним расположением шатуна, т.к. у него средняя скорость иглы ниже, чем у механиз­мов с нижним расположением шатуна.

1. Выбор иглы.

Основным рабочим органом швейной машины является игла. Она предназначена для прокола материала, проведения через него верхней нити и образования петли-на­пуска.

Игла состоит из колбы для крепления иглы в игловодителе; лезвия, являющегося рабочей частью иглы; и острия для прокола материала. В лезвии выполнены ушко для заправки верхней нити, короткий желобок для образования петли и длинный же­лобок для предотвращения верхней нити от перетирания.

Все иглы согласно ГОСТу 7322-55 имеют номера с №60 по №300. Номер иглы соответствует диаметру лезвия в мм, умноженному на 100. Так игла №90 имеет диа­метр лезвия 0,9 мм.

При выборе номера иглы следует ориентироваться на сшиваемые ткани и мате­риалы согласно таблице:

Ткани и материалы	Номер иглы
Шелковые типа сорочечной, вискозной	75 – 90
Шелковые с лавсаном	75 –90
Синтетические типа капрона	75 – 90
Чистошерстяные легкие, шерстяные с лавсаном, штапельные и хлоп­чатобумажные с лавсаном	85 – 110
Шерстяные камвольные и тонкосуконные	85 – 130
Шерстяные типа драпа, ворсовые	90 – 130
Грубосуконные, шелковые плащевые прорезиненные односторонние, мех искусственный	90 – 130
Шинельные, многослойные и тяжелые	130 – 210

Для расчетов курсовой работы нам предложена ткань хлопчатобумажная с лав­саном, т.о. выберем иглу №90.

Длина иглы и ее отдельных частей является основным конструктивным парамет­ром, обеспечивающим выполнение технологического процесса сшивания материалов и входящим в число исходных данных для выполнения прочностных расчетов игл. Угол заточки иглы .

Общая длина лезвия иглы от острия до колбы:

l_>1>=L-(l_>2>+l_>3>) мм (1.1)

L – общая длина иглы: в универсальных швейных машинах L=38 мм

l_>2 >– длина колбы, выступающая из игловодителя: в зависимости от лапки принимает-

ся l_>2>=8-9 мм

l_>3> – длина колбы, закрепляемой в игловодителе, мм

l_>3>=5d мм (1.2)

d – диаметр иглы, мм

Иглы изготавливаются из стальной углеродистой отожженной проволоки марки И3 класса А ГОСТ 5468-60. После изготовления подвергаются закалке до твердости по Роквеллу HRC_>54-60>.

Мы выбрали иглу №90, следовательно d=0,9 мм, примем длину l_>2>=8,5 мм, длина l_>3>=4,5 мм. Тогда общая длина лезвия, согласно формуле (1.1) l_>1>=25 мм

3. Расчет иглы на прочность.

Чем меньше диаметр лезвия иглы, тем меньше вероятность повреждения сши­ваемых тканей. Однако слишком тонкая игла под действием усилия прокола может изогнуться и даже сломаться. Поэтому, чтобы удостовериться в правильности выбора номера иглы и длины ее лезвия, выполняется проверочный расчет иглы на продоль­ный изгиб и на сжатие.

Если усилие прокола P не превышает некоторой предельной величины P_>кр.>, то игла будет испытывать обычное сжатие и ее ось останется прямолинейной. Если уси­лие прокола достигнет предельной величины силы P=P_>max>+P_>кр.>, то она изогнется.

Условие устойчивости иглы по продольному изгибу:

P<[P] (1.3)

где [P] – допускаемое усилие.

(1.4)

где n_>уст.> – коэффициент запаса устойчивости: для стали n_>уст.>=1,8 – 3,0.

Критическая сила:

(1.5)

где Е – модуль упругости материала иглы: для стали Н/мм²

 - коэффициент приведения длины иглы: для данного случая =2

I_>min> – момент инерции ослабленного сечения иглы

мм⁴ (1.6)

В нашем случае I_>min>0,0185 мм²

P_>кр.>14,607 Н

[P]7,3 Н

По нашему условию Р=5,5 Н  Р<[P].

Вывод: выбранная игла подходит по условию устойчивости иглы по продоль­ному изгибу.

Условие прочности иглы по напряжениям сжатия:

(1.7)

где [_>сж>] – допускаемое напряжение на сжатие: для стали И3 [_>сж>]=60 – 90 Н/мм²

F_>min> – площадь поперечного сечения в ушке иглы

F_>min>0,385 d ² мм² (1.8)

В нашем случае F_>min>0,312 мм²

_>сж>17,6 Н/мм²

Отсюда мы видим: _>сж > [_>сж>], следовательно выбранная нами игла подходит по условию прочности иглы по напряжениям сжатия.

Общий вывод: выбранная нами игла пригодна.

4. Выбор геометрических параметров кривошипно-ползунного механизма.

Для центральных механизмов радиус кривошипа:

r=l_>AB>=0,5 S_>o> м (1.9)

где S_>o>- общий ход иглы, равный сумме перемещения иглы от крайнего верхнего по-

ложения до начала входа иглы в материал и перемещения в материале.

Длина шатуна вычисляется по формуле: l = l_>BC >= r/ м (1.10)

По нашему условию S_>o>=м, а =0,38; таким образом r=м, а l0,039

5. Кинематический анализ кривошипно-ползунного механизма.

1. Задачи анализа.

Исходными данными для кинематического анализа являются: схема механизма, длина звеньев и закон движения входного звена (кривошипа).

Задачи кинематического анализа:

• Построение плана положений звеньев механизма.

• Определение линейных скоростей и ускорений точек звеньев.

• Определение угловых скоростей и ускорений звеньев.

2. Построение плана механизма.

Для кинематического исследования строится кинематическая схема механизма, на которой изображается ряд положений всех звеньев механизма (план механизма).

План механизма строится в некотором масштабе. Если кривошип r=l_>AB> на плане механизма изображается отрезком в мм, то длина этого отрезка называется мас­штабным значением длины кривошипа. Тогда истинное значение длины кривошипа:

м (1.11)

где k_>l> – масштаб длин (масштаб плана механизма).

м/мм (1.12)

Масштаб длин соответствует числу метров истинной длины звеньев в одном миллиметре чертежа и является размерной величиной, в отличие от чертежных мас­штабов.

В выбранном масштабе вычисляются длины отрезков на чертеже, соответствую­щих остальным звеньям:

мм (1.13)

На основании исходных данных зададим величину отрезка 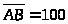мм, тогда масштаб механизма k_>l>=0,00015 м/мм, а длина отрезка соответствующего шатуну мм.

Проведем траекторию движения точки В, радиусом 100 мм, и разделим ее на 8 частей. Примем крайнее левое положение кривошипа за нулевое. По ходу движения присвоим номера положениям кривошипа. Для нахождения положений ползуна, соотвотствующих положениям кривошипа, из точек В_>0>, В_>1>, etc., радиусом проводим дуги до пересечения с прямой АС. Соединяя соответствующие точки, показываем кривошип и шатун в различных положениях. Для одного из положений (в нашем случае для первого) на звеньях укажем центры масс тяжести S_>1> (для кривошипа) и S_>2> (для шатуна). =50 мм; =91 мм.

3. Построение плана скоростей.

План скоростей позволяет вычислить линейную скорость любой точки звеньев, угловую скорость звеньев и служит основой для нахождения уравновешивающего

момента по способу профессора Н.Е. Жуковского.

Определим для первого положения линейную скорость точек A, B, C, S_>1>, S_>2> и угловую скорость шатуна _>2>. Входным является кривошип АВ, вращающийся с угловой скоростью _>1>=const, Частота вращения n_>1>=2500 об/мин.

Точка В является общей для звеньев 1 и 2. Звено 1 совершает вращательное движение. Следовательно величина скорости точки В:

м/с (1.14)

где - угловая скорость кривошипа, 1/с;

l_>AB> – истинная длина кривошипа, м;

n_>1> – частота вращения кривошипа, об/мин

Исходя из нашего условия V_>B>=3,93 м/с

Вектор скорости характеризуется точкой приложения (в точке В), линией действия (по касательной к траектории в точке В, либо перпендикулярно кривошипу АВ) и направлением (по часовой стрелке согласно направлению вращения кривошипа).

Точка С принадлежит звеньям 2 и 3 и движется вдоль прямой АС вместе со звеном 3. Следовательно, линия действия вектора скорости известна, а модуль и направление неизвестны. Точки В и С принадлежат одному звену – шатуну ВС, поэтому между скоростями этих точек есть определенная связь.

Шатун ВС в абсолютном движении относительно неподвижного звена – стойки совершает плоское (плоскопараллельное) движение. Которое можно представить в виде сумм двух простых движений: переносного (поступательного) и относительного (вращательного). При поступательном движении точки описывают одинаковые траектории, любая прямая, принадлежащая звену, остается параллельной самой себе, скорости всех точек равны между собой и параллельны, а угловая скорость равна нулю.

(1.15)

Однако, в абсолютном движении относительно стойки точка С движется вместе с ползуном вдоль прямой АС, поэтому действительной положение точки С определяет- ся относительным вращательным движением шатуна ВС вокруг точки В. Поэтому абсолютная скорость точки С:

(1.16)

где V_>BC> – относительная скорость точки С при повороте шатуна ВС вокруг точки В.

Примем точку В за полюс, т.к. нам известны все характеристики вектора скорости ; у вектора скорости известна только линия действия, расположенная перпендикулярно радиусу вращения ВС; у вектора скорости известна тоже только линия действия.

Для определения векторов скорости и решим векторное уравнение (1.16). План скоростей как раз и представляет собой графическое решение векторных уравнений.

Для построения плана скоростей задается его масштаб:

(1.17)

где P_>V3>b – длина отрезка, изображающего на плане скоростей скорость точки В, мм

Пусть P_>V3>b=130 мм, тогда k_>v>=0,03

Из полюса на плане скоростей P_>V3> откладываем отрезок прямой перпендикулярно звену АВ_>3> в сторону его движения. Затем через точку b линию действия вектора вращательной скорости перпендикулярно звену В_>3>С_>3>, а из полюса P_>V3> параллельно траектории точки С_>3> при поступательном движении проводим линию действия вектора абсолютной скорости до пересечения с линией действия вектора скорости в точке с. Отрезок соответствует абсолютной скорости точки С, отрезок - вращательной скорости точки С вокруг В. Модули этих скоростей:

м/с

м/с

Направления векторов скоростей и определяются согласно векторному уравнению (1.16).

Для определения какой-либо промежуточной точки звена (центра тяжести S_>2 > звена ВС) используют свойство подобия:

мм

Отрезок откладываем на плане скоростей от точки b в такую сторону, чтобы последовательность точек на звене ВС соответствовала последовательности точек на плане скоростей. Соединив точку S_>2> c полюсом плана, получим отрезок , соответствующий в масштабе плана скоростей скорости точки S_>2>.

м/с

Аналогично находится модуль точки S_>1>:

м/с

Скорость точки А, принадлежащей кривошипу 1 и стойке, равна нулю, и на плане скоростей будет совпадать с полюсом плана скоростей.

На основании плана скоростей находим мгновенное значение модуля и направления угловой скорости _>2> шатуна. Согласно уравнению (1.14) модуль угловой скорости:

1/с

Для определения направления угловой скорости _>2 >вектор скорости с плана скоростей мысленно переносится в точку С и увязывается направление вращательной скорости с направлением угловой скорости _>2 > шатуна.

Аналогичным образом строятся остальные планы скоростей и находятся скорости точек:

V_>BС1>=2,25 м/с V_>C1>=2,76 м/с

V_>BС2>= V_>C2>=

V_>BС4>= V_>C4>=

V_>BС5>=2,79 м/с V_>C5>=3,6 м/с

V_>BС6>= V_>C6>=

V_>BС7>=3,12 м/с V_>C7>=4,02 м/с

V_>BС0>= V_>C0>=

4. Построение плана ускорений.

План ускорений позволяет определить линейное ускорение любой точки всех звеньев, угловое ускорение звеньев является основой для вычисления инерционных факторов в силовом расчете механизма.

Точка В описывает криволинейную траекторию, следовательно, полное (абсолютное) ускорение складывается из двух составляющих:

(1.18)

где - вектор нормального (центростремительного) ускорения

- вектор касательного ускорения

Модуль касательного ускорения:

(1.19)

где _>1> – угловое ускорение кривошипа 1.

, т.к. по условию _>1>=const

Следовательно, полное ускорение точки В:

(1.20)

Модуль нормального ускорения:

(1.21)

В нашем случае 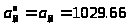м/с². Линия действия ускорения совпадает с радиусом (звеном 1 - кривошипом), и направленно это ускорение к центру вращения (полюсу).

На основании предыдущего раздела 1.5.3. абсолютное ускорение точки С:

(1.22)

где - ускорение точки С во вращательном движении звена ВС вокруг полюса В.

Ускорение точки С по аналогии с уравнением (1.18) может быть представлено в виде сумм двух составляющих:

(1.23)

где - вектор нормального ускорения точки С в ее вращательном движении

вокруг полюса В.

- вектор касательного ускорения

Модуль нормального ускорения по аналогии с уравнением (1.21):

м/с²

Линия действия вектора совпадает с шатуном 2, направленно это ускорение к точке В_>1>.

Для вектора касательного ускорения известна только линия действия, расположенная перпендикулярно нормальному ускорению , т.е. звену ВС. Точка С совершает поступательное движение вместе с ползуном, поэтому линия действия полного ускорения параллельна траектории точки С при поступательном движении. Уравнение (1.23) содержит две неизвестных величины, поэтому его можно решить графическим путем.

Возьмем за полюс плана ускорений точку P_>a3>, а отрезок пусть будет равен 150 мм (длина отрезка, соответствующая на плане ускорений ускорению точки В). Тогда масштаб плана ускорений:

Длина отрезка, изображающая на плане ускорений ускорение :

мм

Из полюса ускорений P_>a3> проводим луч параллельный звену АВ_>3>, и на нем в направлении к точке А откладываем отрезок , соответствующий ускорению точки В. Из конца этого отрезка – точки В – проводим луч и откладываем на нем в сторону точки В_>3> отрезок , соответствующий, согласно уравнению (1.23), вектору ускорения . Перпендикулярно отрезку проводим луч, а из полюса плана P_>a3> проводим другой луч ло пересечения с первым в точке с. Длина отрезка соответствует в заданном масштабе плана ускорению , отрезок - ускорению . Модули этих ускорений:

м/с²

м/с²

В соответствии с уравнением (1.23) показываем направления всех векторов ускорения.

Ускорения для промежуточных точек определяются по свойству подобия. , а . Таким образом мм. Откуда получим:

м/с²

м/с²

Модуль углового ускорения шатуна 2 можно вывести из формулы (1.19):

1/с²

Перенесем вектор ускорения с плана ускорений в точку С_>3> плана механизма, и увидим, что угловое ускорение _>2> направлено против часовой стрелки.

6. Расчет уравновешивающего момента.

При расчете мощности двигателя необходимо знать величину уравновешивающего (движущего) момента, приложенного к главному валу для обеспечения заданного закона его движения (_>1>=const). Решить поставленную задачу можно методом профессора Н.Е. Жуковского.

Согласно теореме профессора Н.Е. Жуковского, если силу, приложенную к какой-либо точке звена механизма, перенести параллельно самой себе в одноименную точку повернутого на 90^о плана скоростей, то момент этой силы относительно полюса плана скоростей будет пропорционален ее мощности.

На основании общего уравнения динамики:

(1.24)

где Ni – мощность i-той внешней силы;

Nuj – мощность j-той силы инерции.

В соответствии с теоремой профессора Н.Е. Жуковского уравнение (1.24) равносильно уравнению моментов сил относительно полюса повернутого плана скоростей:

(1.25)

По условию нам дано, что m_>3>=0,035 кг (масса поступательно движущихся частей кривошипно-ползунного механизма), масса кривошипа (исходя из того, что в 1 мм содержится 2 грамма) m_>1>=0,03 кг, масса шатуна (исходя из того, что в 1 мм содержится 2,5 грамма) m_>2>=0,0975 кг, сила полного сопротивления =5,5 Н.

Момент инерции шатуна относительно центра масс S_>2> можно определить по зависимости:

(1.26)

Вычерчиваем план механизма в первом положении без изменения масштаба, т.е. k_>l>=0,00015 м/мм.

Определяем силовые факторы, приложенные к звеньям.

Силы тяжести:

G_>1>=m_>1>g=0,29 Н

G_>2>=m_>2>g=0,96 H

G_>3>=m_>3>g=0.34 H

Все звенья движутся с ускорением, следовательно, к ним приложены силы инерции:

(1.27)

где - вектор полного ускорения центра масс.

Знак минус в уравнении (1.27) означает, что сила инерции и ускорение центра масс направлены в разные стороны.

Модули сил инерции:

Н

Н

Н

Момент инерционных сил, приложенных к шатуну 2:

(1.28)

Знак минус показывает, что направления момента инерционных сил и углового ускорения разные.

Момент инерции шатуна, согласно уравнению (1.26):

Момент инерционных сил, согласно уравнению (1.28): . Направлен этот момент по часовой стрелке.

Момент инерционных сил и уравновешивающий момент заменим парами сил.

Н

(1.29)

Составляющие силы прикладываем перпендикулярно звену ВС в шарниры В, С и в такую сторону, чтобы они создали момент М_>U>_>2> того же направления (по часовой стрелке). Произвольно задавая направление уравновешивающего момента в сторону вращения кривошипа, прикладываем составляющие силы в шарниры А и В так, чтобы они образовали уравновешивающий момент против часовой стрелки.

Прикладываем в соответствующих точках звеньев силы тяжести, силу полезного сопротивления и силы инерции, ориентируясь на направления векторов ускорения центров масс по плану ускорений.

Строим повернутый на 90^о по часовой стрелке план скоростей, прикладываем к нему в соответствующих точках все силы.

Уравнение моментов всех сил, относительно полюса плана скоростей:

Откуда мы можем найти =5,13 Н.

Уравновешивающий (движущий) момент:

(1.30)

где =1,3 – 1,5 – коэффициент, учитывающий влияние сил трения во во вращатель-

ных и поступательных парах.

М_>ур>=0,11

7. Расчет мощности двигателя для привода механизма иглы.

Мощность на главном валу, необходимая для привода механизма иглы:

Вт

Требуемая мощность двигателя:

Вт

где _>рп>=0,94 – 0,96 – КПД клиноременной передачи.

Определив требуемую мощность для привода остальных механизмов швейной машины, можно выбрать электродвигатель.

2. Условия для расчетов.

Сила полного сопротивления, Н	5,5
n>1>,> >об/мин	2500
е, м	0
m>3>, кг	0,035
Общий ход иглы, м	0,03
Материал	Хлопчатобумажная ткань с лавсаном.
	135о
	0,38

Масса кривошипа расчитывается из расчета, что в одном мм кривошипа содержится 2 гр; в одном мм шатуна – 2,5 гр.

3. Литература.

1. Вильщиков Н.М. и др. Расчет и проектирование машин швейного производства. Л. “Машиностроение”, 1973, 344 с.

2. Червяков Ф.И., Николаенко А.А., Швейные машины, М. “Машиностроение”, 1976, 416 с.

3. Кинасошвили Р.С., Сопротивление материалов, М. “Наука”, 1975, 384 с.

4. Артоболевский И.И., Теория механизмов и машин, М., “Наука”, 640 с.

5. Боронин Н.Н., ТММ, Разделы “Силовой анализ плоского механизма” и “Кинематический синтез кулачкового механизма”, методические указания к решению задач, Л. ЛФ МТИ, 1985, 32 с.