СТАТИСТИКА (работа 11)
Министерство по налогам и сборам Российской Федерации
В
с е р о с с и й с к а я г о с у д а р с т в
е н н а я н а л о г о в а я а к а д е м и я
СТАТИСТИКА
КОНТРОЛЬНая работа
Выполнила: студентка группы К4
Фак-та Управления
Могученко Анна Павловна
Проверил: Соколин В.П.
Москва – 2001
Задача 1
Требуется определить значения следующих показателей:
1. Средняя трудоемкость изготовления изделия
2 Средний уровень выработки
3. Средний уровень оплаты труда
4. Средний уровень фондоотдача
Рассчет в таблицах 1,2,3,4.
Методические указания
Расчёт средних по результатам группировки.
Данные для расчета и анализа средних величин могут быть представлены в сгруппированном виде, когда для каждого значения усредняемого признака Х сообщается частота его повторения. В этих случаях средняя величина рассчитывается по обычным формулам средних взвешенных (арифметических либо гармонических). Если в сгруппированных данных указывается не конкретное значение признака Х по каждой группе, а лишь интервал его изменения, то в этом случае необходимо получить среднее значение признака по каждой группе. А далее используются обычные формулы средних взвешенных. Если же средние значения признака в группах определить по имеющимся сведениям нельзя, то их заменяют условно значениями центра интервалов. В результате получают ряд распределения, аналогичный дискретному, где в качестве значений дискретного признака будут выступать центры интервалов а>i>>, >а в качестве весов признака F>i > - количество элементов ряда для интервала i.
Таким образом, расчет средней арифметической делают по формуле

Показатель себестоимости является вторичным признаком, так как он задан на единицу первичного признака (объем продукции, выраженный абсолютной величиной) и может быть представлен как отношение двух первичных признаков, а именно затрат на производство и объём продукции:
С = ЗП / ОП, где С — себестоимость, ЗП — затраты на производство, ОП —. объем продукции.
Следовательно, для расчета средней себестоимости по каждому предприятию следует вычислить среднюю взвешенную. Нужно выбрать: арифметическую или гармоническую?
Выбор вида средней усредняемого признака выполняется по следующим правилам.
1. Если в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя величина вычисляется непосредственно по этой формуле.
2. Если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателя её логической формулы, а значения числителя не известны, но могут быть найдены как произведения этих показателей, то средняя должная вычисляться по формуле средней арифметической взвешенной.
3. Если известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя вычисляется по формуле средней гармонической.
Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности — носители признака, а произведения этих единиц на значения признака (т. е. m = X*f). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т. д.) предприятиям, рабочим, занятым изготовлением одного итого же вида продукции, одной и той же детали, изделия.
Общее требование к формуле расчета среднего значения состоит в том, чтобы все этапы расчета имели реальное содержательное значение. Полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения усредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный с усредняемым. Этот итоговый показатель является определяющим в том смысле, что его связь с индивидуальным значением признака определяет способ расчета средней величины.
Расчет средних через показатели структуры
Средние арифметические и средние гармонические могут быть как простыми, так и взвешенными. Веса в формулах средних показывают повторяемость данного значения признака.
Величина средней зависит не от самих абсолютных значений весов отдельных элементов, а от пропорций между ними. Поэтому вместо абсолютных значений для взвешивания можно брать веса вариантов, выраженные в долях единицы или в процентах. Допустим, что требуется вычислить среднюю величину для некоторой совокупности вариантов (x>1> + x>2>+...+ x>n>) с соответствующими частотами (n>1> + n>2>+...+ n>n>). Отношения отдельных частот n>1>, n>2> и т. д. к сумме частот представляют доли рi отдельных вариантов из всей совокупности или удельные веса этих вариантов (частности).
Можно
записать, что X = X1*p1+Х2* р2+...+Хп*рп= ∑х>i>
* р>i> ;
т. е. мы от абсолютных значений весов
частот перешли к относительным
(частностям).
Из этого свойства вытекает очень важное практическое правило. Если неизвестны абсолютные значения весов, но известны пропорции между ними, то мы можем пользоваться этими пропорциями для взвешивания. Допустим, что одно предприятие будет выпускать продукт по цене 10 руб., а второе - этот же продукт по цене 15 руб. Неизвестно точно, сколько продукции выпустит каждое предприятие, но известно, что второе предприятие выпустит продукции в 2 раза больше, чем первое. Тогда можно вычислить среднюю цену так: х = (10 *1 + 15 *2) / 3= 13,3 руб.
То же правило применяется в тех случаях, когда неизвестны абсолютные величины весов, но известны какие-то другие значения, которые связаны с этими весами. Вместо абсолютных значений можно брать эти производные величины. Например, если известно, что на первом предприятии в 2 раза больше рабочих, чем на втором, то можно условно предположить, что и продукции первое предприятие выпускает больше, чем второе тоже вдвое.
Если удельные веса заданы не в долях, а в процентах, тогда:

где р - удельный вес каждого варианта в процентах.
Средняя трудоемкость изготовления изделия одного и того же вида несколькими рабочими (t):
г
де
t,
— трудоемкость изготовления
единицы продукции конкретным рабочим;
d(Q)— доля рабочего в общем объеме произведенной продукции;
d(T) — доля рабочего в общих затратах рабочего времени.
Средняя трудоёмкость изготовления изделия
Таблица1
|
Рабочий |
Трудоёмкость
изготовления изделия, |
Центральное
значение интервала, |
Объем продукции, штук |
Доля рабочего в общем объеме произведенной продукции, % |
Затраты
рабочего времени, |
Доля
рабочего в общих затратах рабочего
времени, |
|
1 |
2 |
3 |
4 |
6 |
5 |
7 |
|
1. |
9-12 |
10,5 |
30 |
35 |
350 |
20 |
|
2. |
12-15 |
13,5 |
26 |
26 |
160 |
29 |
|
3. |
15-18 |
16,5 |
32 |
23 |
390 |
34 |
|
4. |
18 — 21 |
19,5 |
47 |
16 |
280 |
17 |
|
Итого: |
--- |
135 |
100 % |
1180 |
100 % |
|
|
Средняя
трудоёмкость изготовления изделия,
|
15,67 |
14,11 |
14,30 |
14,29 |
1)
2)
2
.
Средний уровень выработки
продукции в единицу рабочего
времени (W).
Рассчитывается он по формулам
где W—уровень выработки для отдельного объекта (предприятия, цеха, участка, рабочего);
d(Т) — доля данного объекта (предприятия, цеха, участка, рабочего) в общих по всей совокупности затратах рабочего времени;
d(Q) — доля объекта i в общем выпуске продукции.
Средний уровень выработки на одного рабочего
Таблица 2
|
Рабочий |
Выработка
на одного рабочего, |
Центральное
значение интервала, |
Объем продукции, штук |
Доля рабочего в общем объеме произведенной продукции, % |
Затраты
труда рабочего, |
Доля
рабочего в общих затратах труда
рабочего, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1. |
7 - 8 |
7,5 |
15 |
34 |
14 |
34 |
|
2. |
8 - 9 |
8,5 |
29 |
29 |
26 |
11 |
|
3. |
9 - 10 |
9,5 |
38 |
19 |
37 |
26 |
|
4. |
10 - 11 |
10,5 |
57 |
18 |
54 |
29 |
|
Итого: |
-- |
139 |
100 |
131 |
100 |
|
|
Средняя выработка на
одного рабочего, |
--- |
9,9 |
9,0 |
9,7 |
9,0 |
1)
2)
3. Средний уровень оплаты труда (Т):

,где f — уровень оплаты в единицу времени на объекте i;
d(Т) — доля объекта i. в общих трудозатратах;
d(F)—доля объекта i в общем суммарном фонде оплаты труда.
Средний уровень оплаты труда рабочего
Таблица 3
|
Рабочий |
Уровень
оплаты труда рабочего, |
Центральное
значение интервала, |
Фонд оплаты труда, тыс. руб. |
Доля рабочего в общем Фонде оплаты труда, % |
Затраты
труда рабочего, |
Доля
рабочего в общих затратах труда
рабочего, |
|
1 |
2 |
3 |
4 |
6 |
5 |
7 |
|
1. |
1 – 3 |
2 |
16 |
18 |
18 |
29 |
|
2. |
3 – 5 |
4 |
29 |
34 |
27 |
34 |
|
3. |
5 – 7 |
6 |
64 |
29 |
16 |
11 |
|
4. |
7 - 9 |
8 |
159 |
19 |
19 |
26 |
|
Итого: |
-- |
268 |
100 |
80 |
100 |
|
|
Средний уровень оплаты
труда рабочего, |
--- |
5,88 |
4,05 |
5,44 |
4,68 |
1)
2)


4
.
Средний уровень фондоотдачи (Н):
где Н — уровень фондоотдачи (стоимость произведенной продукции, руб.) на 1 руб. основных производственных фондов по объекту (отрасли, предприятию) i;
d(G) — доля объекта i в общей стоимости фондов по всей изучаемой совокупности;
d(Q) — доля объекта i в общем выпуске продукции.
Средний уровень фондоотдачи
Таблица 4
|
Вид оборудования |
Уровень
фондоотдачи, |
Центральное
значение интервала, |
Объем произведенной продукции, тыс. руб. |
Доля оборудования в общей стоимости фондов, % |
Стоимость основных производственных фондов, тыс. руб. |
Доля
оборудования в общем объеме выпуска
продукции, |
|
1 |
2 |
3 |
4 |
6 |
5 |
7 |
|
А. |
1 – 3 |
2 |
164 |
31 |
325 |
18 |
|
Б. |
3 – 5 |
4 |
117 |
24 |
450 |
19 |
|
В. |
5 – 7 |
6 |
133 |
12 |
250 |
31 |
|
Г. |
7 - 9 |
8 |
221 |
33 |
300 |
32 |
|
Итого: |
-- |
635 |
-- |
1325 |
||
|
Средний уровень фондоотдачи |
--- |
3,45 |
4,94 |
5,30 |
4,37 |
1)

2)
1. Средняя трудоёмкость изготовления изделия
d(Q)1=30:135=0,22; d(Q)2=26:135= 0,19 ;d(Q)3 = 32:135=0,24 ; d(Q)4=47:135=0,35

d(T)1=350:1180=0,3; d(T)2=160:1180=0,14; d(T)3=390:1180=0,33; d(T)4=280:1180=0,24

2. Средний уровень выработки на одного рабочего
d(Q)1=15:139=0,11; d(Q)2=0,21; d(Q)3=0,27; d(Q)4=0,41

d(T)1=14:131=0,11; d(T)2=0,20; d(T)3=0,28; d(T)4=0,41

3. Средний уровень оплаты труда рабочего
d(T)1=18:80=0,23; d(T)2=0,34; d(T)3=0,20; d(T)4=0,24

d(F)1= 16:628=0,06; d(F)2= 0,11; d(F)3=0,24; d(F)4=0,59

 1/0,17=5,88
1/0,17=5,88
4. Средний уровень фондоотдачи
d(G)1=164:635=0,26; d(G)2=0,18; d(G)3=0,21; d(G)4=0,35

d(Q)1=325:1325=0,25; d(Q)2=0,34; d(Q)3=0,19; d(Q)4=0,23

Задача 2.
ПОКАЗАТЕЛИ, ХАРАКТЕРИЗУЮЩИЕ ТЕНДЕНЦИЮ РЯДА ДИНАМИКИ
По данным о численности работников предприятия по годам определить показатели, характеризующие тенденцию развития данного явления во времени:
1. Абсолютные приросты базисные (накопленные) и цепные (годовые).
2. Темпы роста базисные и цепные.
3. Темпы прироста базисные и цепные.
4. Абсолютное значение одного процента прироста; темп наращивания одного процента.
5. Средний абсолютный прирост; средний темп роста.
6. Постройте график базисных и цепных темпов роста.
Сделайте выводы на основании расчетов о тенденции динамики численности работников предприятия.
Рассчет показателей в таблице 5.
Методические указания
1. Абсолютным приростом в статистике называется разность двух уровней ряда динамики. Абсолютный прирост характеризует размер увеличения или уменьшения уровня ряда динамики за определенный период времени. Абсолютный прирост определяется для двух произвольных уровней динамики ряда -- смежных или крайних уровней.
Величина этого показателя за смежные периоды или моменты времени рассчитывается по формуле
∆х
= X>i>
–
X>i>>-1>,
где ∆Х - абсолютный прирост;
X>i>
- любой уровень ряда, начиная от
второго;
X>i>>-1>
- уровень, непосредственно
предшествующий уровню X>i>.
Абсолютный прирост (базисный) определяется по формуле:
∆х = Xi – X1 где X1 – начальный (базисный) уровень ряда
За период в целом абсолютный прирост определяется по формуле ∆Х = Хп – X1 , где X1 - начальный уровень ряда; Хп - конечный его уровень.
2. Для характеристики относительной скорости изменения уровня ряда динамики в единицу времени используются показатели темпа роста и темпа прироста.
Темпом роста Кр называется отношение одного уровня ряда динамики к другому уровню, принятому за базу сравнения. Темпы роста обычно выражаются либо в процентах, либо в виде простых отношений. Темпы роста выраженные в виде простых отношений, называются коэффициентами роста.
Отдельные значения уровня ряда динамики могут быть выражены к одному и тому же уровню (обычно начальному) или к предшествующему уровню. В первом случае база будет постоянной, во втором - переменной. Темпы роста, исчисленные к постоянной базе, называются цепными.
Базисные темпы роста рассчитываются по формуле Кр = Xi:/X1
Цепные темпы роста рассчитываются по формуле Кр = Xi:/ Xi-1
Отношение абсолютного прироста к уровню, принятому за базу, называется темпом прироста.
Численность работников на предприятии за 1995 - 2000 гг. Таблица5
|
Годы |
Численн Работн. чел. |
Абсолютный прирост, чел. |
Темпы роста, % |
Темпы прироста, % |
Абсолютная величина 1-го-% прироста |
|||
|
Цепной |
базисный |
цепной |
базисный (к 1997 году) |
цепной |
базисный |
|||
|
1995 |
1300 |
---------- |
-------- |
------------ |
100 |
------- |
-------- |
-------- |
|
1996 |
1350 |
1350-1300=50 |
1350-1300=50 |
1350/1300*100= 104 |
1350/1300*100= 104 |
4,0 |
4,0 |
13,50 |
|
1997 |
1380 |
1380-1350=30 |
1380-1300=80 |
1380/1350*100= 102 |
1380/1300*100= 106 |
2,0 |
6,0 |
13,80 |
|
1998 |
1400 |
1400-1380=20 |
1400-1300=100 |
1400/1380*100=101 |
1400/1300*100=108 |
1,0 |
8,0 |
14,0 |
|
1999 |
1600 |
1600-1400=200 |
1600-1300=300 |
1600/1400*100=114 |
1600/1300*100=123 |
14,0 |
23,0 |
16,0 |
|
2000 |
1700 |
1700-1600=100 |
1700-1300=400 |
1700/1600*100=106 |
1700/1300*100=131 |
6,0 |
31,0 |
17,0 |
3. Относительные величины динамики, кроме показателей темпа роста, абсолютный прирост, характеризуются такими показателями: темп прироста и абсолютная величина одного процента прироста.
Темп
прироста определяется
путем деления абсолютного прироста на
абсолютную величину, характеризующую
изучаемое явление за предыдущий
период.
или темп прироста можно
определить путем вычитания из каждого
темпа роста единицы, если темп роста
выражен в коэффициентах, или 100%
- если темп роста выражен
в процентах.
Темпы прироста показывают прирост или снижение (изменение) явления по сравнению со 100%.
Коэффициент, или темп прироста, ∆Кприр. , как базисный, так и цепной, определяется по формулам, если
• показатели темпов исчислены в процентах: ∆Кприр. =Кр - 100%
• показатели темпов исчислены в коэффициентах: ∆Кприр. =Кр -1.
При вычислении граф 8 и 7 табл. 16 использована формула исчисления показателей темпов роста в процентах, т.е. ∆Кприр. =Кр - 100%.
4. Абсолютное значение одного процента прироста
Показатель абсолютного значения одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах. В буквенном выражении этот показатель может быть представлен в виде следующего соотношения:
(Xi - Xi – 1) / ∆Кприр. *100, где ∆Кприр. - цепной рост прироста.
Так как ∆Кприр. = (Xi - Xi –1) / Хi –1, то из приведенного выше соотношения нетрудно установить, что абсолютное значение одного процента прироста равно 0,01 предшествующего уровня.
Показатель абсолютного значения одного процента прироста играет весьма важную роль в экономическом анализе.
5. Исчислим средние показатели, характеризующие динамический ряд, т.е. изменение численности работников предприятия в среднем за 6 лет. Этими показателями являются средние или среднегодовые абсолютные приросты и средние или среднегодовые темпы роста. Исчисляются они по следующим формулам:



Среднегодовой темп роста исчислили по формуле через значения уровней ряда. Но для расчета этого показателя может применяться и другая формула - средняя геометрическая. Она основана на перемножении цепных темпов роста (так как проценты и коэффициенты никогда не суммируются, что является грубой ошибкой, их можно только перемножать):
Между цепными и базисными темпами роста существует следующее правило (взаимосвязь): произведение цепных темпов роста равно конечному базисному.
В нашем примере можно обойтись без перемножения, а взять из табл.5 последнее значение базисного темпа роста (отношение уровня 2000 г. к уровню 1995 г.). Оно равно 131,0%, или в коэффициентах 1,310.. Из этого числа извлекаем корень пятой степени и получаем 1,0554 , или 105,54%.
 1,0554
1,0554
Зная среднегодовой темп роста, можно определить среднегодовой темп прироста по формуле

Розничный товарооборот за период с 1995г. по 2000 г. в среднем возрастал за год на 5,54% (в абсолютном выражении - на 17 чел.).
6. На основании исчисленных темпов роста (базисных и цепных) построим график (рис..1).
7. На основании расчетов и графика сделаем следующие выводы. Рассмотрим базисные темпы роста. Так, численность работников предприятия в 2000 г. по сравнению с 1995 г. возросла на 131%; в 1996,1997,1998 гг. численность возрастает довольно плавно и не значительно на 104,106,108 % соответственно.
Цепные показатели указывают на рост или снижение значения по сравнению с предшествующим годом. Так, в 1996г по сравнению с базисным возрасла на 104%. 1997 и 1998гг – тенденция к уменьшению численности. В 1999 г. по сравнению с 1998 резко подскачила численность (114%), а в 2000г. опять упал до 106%.

Задача 3
СЕЗОННЫЕ КОЛЕБАНИЯ. МЕТОД ПОСТОЯННОЙ СРЕДНЕЙ
По данным о выгрузке вагонов по отделению железной дороги (тыс. усл. ваг.) :
1) измерить сезонные колебания выгрузки вагонов по отделению железной дороги ( тыс. усл. ваг.), применяя соответствующую формулу индекса сезонности:
2) показатели сезонной волны изобразить графически;
3) на основе синтезированной модели сезонной волны сделайте прогноз объёмов выгрузки вагонов по отделению железной дороги (тыс. усл. ваг.) по месяцам 2001 г. возможного объёма работы в 500 (тыс. усл. ваг.).
Рассчеты представлены в таблице 6.
Методические указания
Сезонными называются периодические колебания, возникающие под влиянием смены времени года.
На изменение уровней ряда динамики внутри года (внутригодовой динамики) оказывают влияние периодические колебания, случайные отклонения и тренд, т.е. общая тенденция развития ряда динамики
Если изучаются сезонные колебания за отдельный год, то обычно тренд не принимается во внимание и отклонения месячных 30-дневных уровней исчисляются от среднемесячного уровня за год.
Для измерения сезонных колебаний важное значение имеет форма сезонной волны, изучаемая с помощью индекса сезонности.
Существует несколько методов расчета индекса сезонности.
Для
рядов внутригодовой динамики, в которых
повышающий или понижающий тренд
отсутствует или незначителен,
средний
индекс сезонности
определяется отношением месячных
уровней
к среднемесячному за год по следующей формуле:

Применение этой формулы для расчетов индекса сезонности носит название способа постоянной средней, так как базой сравнения для всех эмпирических уровней анализируемого ряда динамик является общий средний уровень.
Сезонные колебания выгрузки вагонов по отделению железной дороги (тыс. усл. ваг.)
Таблица 6
|
Г |
1997 |
1998 |
1999 |
Всего
за 3 года |
В
среднем за 3 года |
Индекс
сезонности |
Отклонение
от среднего |
Квадрат
отклонения |
Прогноз
на 2001 г. |
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Январь |
36,3 |
32,1 |
37,3 |
105,70 |
35,23 |
98,35 |
-0,59 |
0,35 |
40,98 |
|
Февраль |
33,2 |
30,0 |
32,2 |
95,40 |
31,80 |
88,78 |
-4,02 |
16,16 |
36,99 |
|
Март |
34,0 |
33 |
42 |
109,00 |
36,33 |
101,42 |
-0,51 |
0,26 |
42,26 |
|
Апрель |
41,9 |
35,8 |
40,9 |
118,60 |
39,53 |
112,30 |
3,71 |
13,76 |
46,79 |
|
Май |
36,8 |
29,1 |
36,8 |
102,70 |
36,57 |
102,09 |
0,75 |
0,56 |
42,54 |
|
Июнь |
42,3 |
30,9 |
40,3 |
113,50 |
37,83 |
105,61 |
2,01 |
4,04 |
44,01 |
|
Июль |
35,3 |
31,4 |
35,3 |
102,00 |
34,00 |
94,92 |
-1,82 |
3,31 |
39,55 |
|
Август |
35,0 |
29,3 |
34 |
98,30 |
32,77 |
91,49 |
-3,05 |
9,30 |
38,12 |
|
Сентябрь |
33,7 |
32,5 |
33,7 |
99,90 |
33,30 |
92,96 |
-2,52 |
6,35 |
38,74 |
|
Октябрь |
36,9 |
35,6 |
34,9 |
107,40 |
35,80 |
99,94 |
-0,02 |
0 |
41,64 |
|
Ноябрь |
35,3 |
34,7 |
35,3 |
105,30 |
35,10 |
97,99 |
-0,72 |
0,52 |
40,83 |
|
Декабрь |
43,7 |
38,2 |
42,7 |
124,6 |
41,53 |
115,94 |
5,71 |
32,60 |
48,31 |
|
Итого: |
444,4 |
392,6 |
445,4 |
1282,40 |
429,79 |
100,0 |
--- |
87,21 |
500,76 |
|
В среднем |
37,03 |
32,72 |
37,12 |
106,87 |
35,82 |
--- |
41,67 |
Рассмотрим применение метода постоянной средней на примере данных таблицы 6.
Данные графы 1 берутся из таблицы исходных данных. Данные граф 2 и 3 остаются неизменными по всем вариантам расчета задания.
В графе 4 табл. 6 сначала суммируются данные по месяцам за три года: для января у>i> =36,3+32,1+37,3=105,7 и т.д.
По формуле
простой средней арифметической для
каждого месяца в графе
5
табл. 6 находим
среднее значение выгрузки в среднем
за три года:
для января
=105,7 : 3 = 35,23
тыс. усл. ваг. и т.д.
В

 итоговой строке "В среднем" графы
5 определен также по
формуле средней арифметической простой
знаменатель формулы индекса сезонности
в виде общего для всего ряда динамики
среднего уровня
за год:
итоговой строке "В среднем" графы
5 определен также по
формуле средней арифметической простой
знаменатель формулы индекса сезонности
в виде общего для всего ряда динамики
среднего уровня
за год:
=429,79
: 12 = 35,82
тыс. усл. ваг.
Этот общий средний уровень и используется в качестве постоянной базы сравнения при определении средних индексов сезонности, которые определены в графе 6 табл. 6: за январь i>si>> >= 35,23 : 35,82 * 100=96,03 %.
М
ерой
сезонных колебаний является среднее
квадратическое отклонение
К
оэффициент
сезонной колеблемости будет:
Характер сезонных колебаний показан на рис. 2. На графике видно, что сезонные колебания выгрузки вагонов характеризуются довольно-таки резким спадом в феврале (-9,57) и тут же резким скачком в марте (+12,64), еще один скачек в декабре (+17,95). В другие месяцы повышения и понижения гладкие.
На основе значений сезонной волны по месяцам выполним прогноз выгрузки вагонов по месяцам 2001 г., если общий объем работы равен за год 500 тыс. усл. вагонов.
Сначала определим средний месячный за год объем выгрузки:
Y = 500 : 12 = 41,67 тыс. усл. ваг.
Прогноз
объемов выгрузки вагонов на каждый
месяц требует полученную сумму
41,67 умножить на значения
соответствующих индексов сезонности
для каждого месяца.
Например, для
января 41,67
*0,9835 = 40,98тыс. усл. ваг.
Полученные результаты расчетов помещены в графе 9 табл.6.
Общая сумма реализации за все 12 месяцев равна исходной сумме 500 тыс. усл. ваг, что свидетельствует о правильности проведенных расчетов.

Задача 4.
СЕЗОННЫЕ КОЛЕБАНИЯ. МЕТОД СКОЛЬЗЯЩЕЙ СРЕДНЕЙ
По данным о выгрузке вагонов по отделению железной дороги (тыс. усл. ваг.) табл.6,7
1) определите характер общей тенденции динамики выгрузки вагонов по отделению железной дороги (тыс. усл. ваг.);
2) применяя соответствующую формулу среднего индекса сезонности, измерить сезонные колебания выгрузки вагонов по кварталам данного четырёхлетия;
3) показатели сезонной волны внутригодового цикла изобразить графически;
4) сделайте краткие выводы.
Рассчет в таблице 7,8.
Методические указания
1. При изучении сезонных колебаний за ряд лет в которых наблюдается повышающий или понижающий тренд применяется методика скользящей средней.
В этом случае индекс сезонности за период определяется отношением эмпирических уровней за период времени к среднему за тот же период по следующей сглаженному у>Ĉi> формуле:

Применение этой формулы для расчетов индекса сезонности носит название способ скользящей средней.
В основу методов положено определение по исходным данным теоретических уровней, в которых случайные колебания погашаются (сглаживаются), а основная тенденция развития явления выражается в виде некоторой плавной линии
В практике встречаются случаи, когда уровень ряда динамики не обнаруживает явно выраженной тенденции роста или падения. Примером этому могут служить нижеприводимые данные о выгрузке вагонов. Чтобы охарактеризовать в подобных случаях основное направление изменения уровня ряда, применяют различные приемы и способы, в частности прибегают к укрупнению интервалов и механическому или аналитическому сглаживанию.
Подсчитав на основе исходных данных количество выгруженных вагонов за каждый квартал года, получим новый ряд динамики.
Этот новый ряд динамики отчетливо показывает, что объем выгрузки вагонов постепенно увеличивается, чего нельзя было сказать на основе месячных данных. Укрупнение интервалов позволило, таким образом, выявить в данном конкретном случае основное направление в изменении уровня ряда динамики.
Расчет базисных темпов роста в табл.7 представлен за четырехлетний период. Он показывает некоторый рост выгрузки вагонов по годам. Так, во втором году по сравнению с первым годом реализация возросла на 6,0% , в третьем году - на 10,7% , в четвертом на 11,0%.
Среднегодовой темп роста

Средний темп прироста равен 5,37% и свидетельствует о незначительной тенденции роста.
|
Выгрузка вагонов по отделению железной дороги (тыс.усл.ваг.) Таблица 7 |
|||||||||
|
Месяц |
1 год |
2 год |
3 год |
4 год |
квартал |
1 год |
2 год |
3 год |
4 год |
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Январь |
32,10 |
32,80 |
37,30 |
36,30 |
I |
95,10 |
98,60 |
111,50 |
103,50 |
|
Февраль |
30,00 |
31,90 |
32,20 |
33,20 |
|||||
|
Март |
33,00 |
33,90 |
42,00 |
34,00 |
|||||
|
Апрель |
35,80 |
39,50 |
40,90 |
41,90 |
II |
99,80 |
111,10 |
114,00 |
121,00 |
|
Май |
29,10 |
36,20 |
36,80 |
36,80 |
|||||
|
Июнь |
34,90 |
35,40 |
36,30 |
42,30 |
|||||
|
Июль |
31,40 |
32,40 |
35,30 |
34,30 |
III |
93,20 |
101,40 |
103,00 |
103,00 |
|
Август |
29,30 |
34,30 |
34,00 |
35,00 |
|||||
|
Сентябрь |
32,50 |
34,70 |
33,70 |
33,70 |
|||||
|
Октябрь |
35,60 |
34,60 |
34,90 |
36,90 |
IV |
111,50 |
112,50 |
113,90 |
116,10 |
|
Ноябрь |
35,70 |
36,30 |
35,30 |
35,30 |
|||||
|
Декабрь |
40,20 |
41,60 |
43,70 |
43,90 |
|||||
|
Итого: |
399,60 |
423,60 |
442,40 |
443,60 |
|
399,60 |
423,60 |
442,40 |
443,60 |
|
В среднем |
35,55 |
32,72 |
37,12 |
36,97 |
|
99,90 |
105,90 |
110,60 |
110,90 |
|
Базисные темпы роста |
|
|
|
|
|
100,00 |
106,01 |
110,71 |
111,01 |
Расчет индекса сезонности
Таблица 8
|
Периоды |
Исходные уровни, тыс. усл. ваг., у>i> |
Скользящие средние, у>с> |
Индекс сезонности, isi |
||
|
Год |
Квартал |
||||
|
1 |
I. |
95,1 |
-- "" -- |
---- |
--- |
|
II. |
99,8 |
(95,1+ 99,8+ 93,2) / 3 = |
96,00 |
1,0392 |
|
|
III. |
93,2 |
(99,8+93,2+111,5) / 3 = |
101,50 |
0,9182 |
|
|
IV. |
111,5 |
и т. д. |
101,10 |
1,1029 |
|
|
2 |
I. |
98,6 |
-- "" -- |
107,10 |
0,9209 |
|
II. |
111,1 |
-- "" -- |
103,70 |
1,0714 |
|
|
III. |
101,4 |
-- "" -- |
108,30 |
0,9360 |
|
|
IV. |
112,5 |
-- "" -- |
108,50 |
1,0372 |
|
|
3 |
I. |
111,5 |
-- "" -- |
112,70 |
0,9896 |
|
II. |
114,0 |
-- "" -- |
109,50 |
1,0411 |
|
|
III. |
103,0 |
-- "" -- |
110,30 |
0,9338 |
|
|
IV. |
113,9 |
(103+113,9+103,5) / 3 = |
106,80 |
1,0700 |
|
|
I. |
103,5 |
(113,9+103,5+121) / 3 = |
112,80 |
0,9200 |
|
|
4 |
II. |
121,0 |
(103,5+121+103) / 3 = |
109,17 |
1.1100 |
|
III. |
103,0 |
(121+103+116,1) / 3 = |
113,37 |
0.9100 |
|
|
IV. |
116,1 |
------ |
---- |
----- |
2. Данные за каждый квартал
используем для расчета индекса сезонности
в табл. 8. Скользящие средние определим
за каждые три последовательные квартала.
Полученное значение скользящей средней
относится к середине интервала. При
вычислении каждой новой средней исключаем
начальный член интервала и присоединяем
очередной уровень ряда: первая скользящая
средняя у1 = (у1 +у2 + у3): 3;
вторая скользящая средняя у2 = (у2 +
у3 + у4): 3 и т. д.
3
.
Тенденцию и колебания наглядно показывает
график рис.
3 . На оси абсцисс отражается время, на
оси ординат –
средний индекс сезонности, который
рассчитывается за каждый квартал
исследуемого периода:
i>si> - сумма значений индексов всех одноименных кварталов за весь период,а n - число лет .
Средние индексы для контрольного примера имеют следующие значения:
I
квартал = (0,9209 + 0,9896 + 0,9200) : 3 = 0,9535
II
квартал = (1,0392 + 1,0714 + 1,0411 + 1,1100) : 4
=1,0654
III
квартал = (0,9182 + 0,9360 + 0,9338 + 0,9100) : 4 = 0,9245
IV
квартал = (1,1029 + 1,0372 + 1,0700) : 3 = 1,0700
4. График сезонной волны выгрузки вагонов показывает, что наибольший объем работы выполняется ежегодно в четвертом квартале с превышением среднегодового значения на 7,0 % и во втором квартале с ростом объема на 6,54 % над среднегодовым значением.

Задача 5.
ПРАКТИКА ИНДЕКСНОГО МЕТОДА
По данным о продаже товаров на оптовом рынке вычислите:
1) общий индекс цен;
2) общий индекс физического объема товарной массы;
3) общий индекс товарооборота в фактических ценах.
4) покажите взаимосвязь индексов в относительном и абсолютном выражениях.
Расчет выполнен в таблице 9,
Методические указания.
Товарооборот в фактических ценах
Таблица 9
|
Товары |
Продано товаров в фактических ценах, млн. руб. |
Индивидуальный
индекс цен, |
Товарооборот
в сопоставимых ценах, млн. руб. |
|
|
Базисный
период, |
Отчетный
период, |
|||
|
1 |
2 |
3 |
4 |
5 |
|
Э. |
200 |
250 |
1,4 |
250:1,4=178,57 |
|
И. |
390 |
600 |
1,19 |
600 : 1,19 = 504,2 |
|
Н. |
430 |
760 |
1,35 |
760 : 1,35 = 562,96 |
|
Итого: |
1020 |
1610 |
--- |
1245,73 |
Определим общий индекс цен
По исходной информации в табл. 9 невозможно исчислить товарооборот в сопоставимых ценах p>0>q>1 > Поэтому воспользоваться формулой агрегатного индекса цен нельзя. Но по условиям задания даны индивидуальные индексы цен i>p>.
Агрегатный индекс цен можно преобразовать в средний из индивидуальных, введя в агрегатный индекс цен значение индивидуального и получив средний гармонический индекс цен.

В агрегатный
индекс цен в знаменатель вместо p>0>
подставим его значение (p>0
> =p>1>
/ i>p>)>
>и получим:
Товарооборот в сопоставимых ценах в табл. 22 (графа 5) будет знаменателем формулы. Его значение получим, разделив товарооборот отчетного периода по каждой группе p>1>q>1 >на соответствующий индивидуальный индекс i>p>.
Определим общий индекс цен:
Товарооборот за счет изменения (роста) цен возрос на 29,24%. Абсолютный прирост товарооборота за счет изменения цен

pq(p)= p>1>q>1> -p>1>q>1> / i>p> = 1610 – 1245,73 = 364,27 млн. руб.
Полученная сумма говорит о том, что был допущен перерасход средств за счет роста цен на 29,24%.
Определим индекс физического объема товарной массы.
По исходной информации в табл.9 невозможно воспользоваться формулой агрегатного индекса физического объема товарной массы.
Агрегатный индекс можно преобразовать в средний из индивидуальных, введя в агрегатный индекс значение индивидуального индекса цен и получив средний индекс.

Вывод. Товарооборот за счет изменения физической массы возрос на 22,13%. Абсолютный прирост товарооборота за счет изменения физической массы
pq(q) = p>1>q>1> / i>p> - p>0>q>0> = 1245,73 - 1020 = 225,73 млн. руб.
Индекс товарооборота в фактических ценах.

Вывод. Товарооборот за счет изменения двух факторов: цен и физической массы возрос на 57,84 %.
Абсолютный прирост товарооборота за счет изменения этих же двух факторов
p q (p, q) = p>1 >q>1> - p>0 >q>0> = 1610 – 1020 = 590 млн. руб.
Выявим взаимосвязи индексов.
В относительном выражении Ipq = Ip * Ig .
Полученные значения индексов подтверждают правильность расчетов из соотношения: 1,5784 = 1,2924 * 1,2213
Товарооборот в отчетном периоде по сравнению с базисным
возрос на 57,84 %, в том числе за счет изменения цен - на 29,24% и за счет изменения физической массы - на 22,13 %.
Взаимосвязь в абсолютном выражении
pq
(p,q)
= pq
(p)
+ pq
(q)
=
= 364,27 млн. руб. + 225,73 млн.
руб. = 590 млн. руб.
Вывод. В абсолютной сумме товарооборот в отчетном периоде по сравнению с базисным возрос на 590 млн. руб., в том числе за счет изменения цен он возрос на 364,27 млн. руб. и за счет изменения физической массы - на 225,73 млн. руб.
Задача 6.
СТАТИКА ПРОИЗВОДИТЕЛЬНОСТИ ТРУДА
Выполнить расчет:
1) индекса производительности труда;
2) влияния на среднюю выработку изменения уровней выработки на отдельных предприятиях и изменение их доли в общеих затратах труда;
3) По итогам расчета таблицы 10 дать краткий анализ изменения средней производительности труда на предприятиях.
Расчет выполнен в таблице 10.
Методические указания.
В статистике рассчитывают два показателя, характеризующие уровень производительности труда.
Первый определяется по формуле: = q/T,
где - уровень производительности труда; q - количество произведенной продукции; Т - затраты труда на изготовление этой продукции.
Второй определяется по формуле: t =T/q,
где t - затраты живого труда на единицу продукции.
Первый показатель называется показателем "выработка", второй - показателем "трудоемкость".
В зависимости от способа исчисления объема продукции статистика различает следующие методы измерения производительности труда: 1) натуральный; 2) стоимостной (ценностной); 3) трудовой.
В настоящем задании рассматривается натуральный метод измерения производительности труда
Натуральный метод измерения производительности труда в наибольшей мере отвечает сущности этого показателя, так как он характеризует эффективность конкретного труда, т. е. труда, создающего определенную потребительскую стоимость. Уровень производительности труда при этом измеряется количеством продукции в соответствующих физических измерениях (тоннах, метрах, литрах и т.д.), в расчете на единицу затраченного рабочего времени - человеко-час, человеко-день или среднее списочное число работников.
Производительность труда, её динамика определяются с помощью индексов - индивидуальных и обобщающих. Натуральные индексы могут быть исчислены на основе прямых или обратных показателей уровня производительности труда. Для выяснения свойства обобщающего индекса производительности труда сопоставим среднюю выработку за два периода по совокупности двух предприятий, изготовляющих одну и ту же продукцию. Для этого обозначим объемы продукции по соответствующим предприятиям в базисном и отчетном периодах через qо и q1 соответственно, а общие затраты труда в базисном и отчетном периодах Т>o> и Т>1> соответственно.
Средний уровень производительности труда в базисном и отчетном периодах тогда:
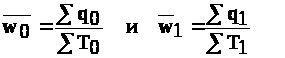

Динамика производительности труда выражается индексом I>>.
Преобразуем указанную формулу. Объем продукции представим как произведение выработки в единицу рабочего времени на общие затраты труда, связанные с изготовлением продукции: *T.
Величина натурального индекса I>>>>производительности труда зависит от двух факторов: от изменения уровней производительности труда на отдельных предприятиях и удельного веса каждого предприятия в общих затратах труда изучаемой совокупности, или, другими словами, от структуры затрат труда.
Индексы, величина которых зависит от указанных факторов, называются индексами переменного состава.
Чтобы исключить влияние изменения структуры затрат на величину производительности труда, необходимо предположить, что структура затрат труда в базисном периоде соответствовала структуре отчетного периода. Для этого нужно, чтобы в предыдущей формуле было соблюдено следующее равенство:

Индекс, устраняющий влияние изменения структуры затрат труда, называется индексом фиксированного состава.
Чтобы определить влияние на среднюю производительность труда изменения удельного веса предприятий в общих затратах труда необходимо предположить неизменными индивидуальные уровни производительности труда. Тогда формула примет следующий вид:

Расчёт:
За два года имеются следующие данные, указанные в табл.10.
Расчет индекса производительности труда
Таблица 10
|
Предприятие |
Базисный период |
Отчетный период |
Индексы |
||||||
|
Объём
продукции, |
Численность
работ-ников, |
Удельный
вес численности работни ков, |
Производитель-ность
труда, |
Объём
продукции, |
Численность
работников, |
Удельный
вес численности работников, |
Производительность
труда, |
W1 / W0 |
|
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
"МАЯК" |
24000 |
1167 |
0,419 |
20,57 |
40200 |
1648 |
0,563 |
24,39 |
1,185 |
|
"СТАРТ" |
17420 |
1620 |
0,581 |
10,75 |
15600 |
1280 |
0,437 |
12,19 |
1,133 |
|
Итого: |
41420 |
2787 |
1 |
14,861 |
55800 |
2928 |
1 |
19,057 |
1,290 |
Выработка на предприятии "МАЯК" возросла на 18,5 %, а на предприятии "СТАРТ" - на 13,3%. В то же время средняя выработка по цеху в целом возросла на 29,0 %, т. е. значительно больше, чем на каждом из двух предприятий. Это объясняется изменением структуры затрат труда: в отчетном году расширился выпуск и возросла доля затрат труда (с 41,9 % до 58,1 %) на предприятии "МАЯК", где производительность труда в 2 раза выше, чем на предприятии "СТАРТ".
У
становим,
как влияют на среднюю выработку изменения
уровней выработки на отдельных
предприятиях и изменение их доли в общих
затратах труда. Для упрощения
расчета заменим в формуле абсолютные
данные по затратам труда (Т) через их
доли (d).
Таким образом, рост выработки в целом за счет повышения ее на двух предприятиях составил 29 %. Расчет индекса I>ω>>.п.с.> = 1,290 указан в графе 9 итоговой строки табл. 10.
Так как для индекса переменного состава выполняется равенство
I>>>.п.с.> = I>>>.ф.с.> * I>>>.стр.сдвига. >= 1,1708 * 1,1028=1,291 ,
произведение индексов совпадает с приведенным в таблице результатом, и это подтверждает - расчеты индексов выполнены, верно.
Статистика оплаты труда.
Оплата труда — это регулярно получаемое вознаграждение за произведенную продукцию или оказанные услуги либо за отработанное время, включая и оплату ежегодных отпусков, праздничных дней и другого неотработанного времени, которое оплачивается в соответствии с трудовым законодательством и коллективными трудовыми договорами.
Перед статистикой оплаты труда стоят следующие основные задачи:
- определение фонда заработной платы и величины выплат социального характера;
- анализ состава и структуры фонда заработной платы;
- определение средней номинальной заработной платы и среднего дохода работников;
- изучение динамики заработной платы и доходов работников;
- определение размера заработной платы отдельных профессиональных групп работников;
изучение дифференциации работников по размеру заработной платы.
Статистические органы должны предоставлять информацию, необходимую для расчетов расходов на рабочую силу и построения системы национальных счетов.
Состав фонда заработной платы
В состав фонда заработной платы входят:
- начисленные предприятиями и организациями суммы оплаты труда в денежной и натуральной формах за отработанное время;
- оплата за неотработанное время;
стимулирующие доплаты и надбавки, компенсационные доплаты и надбавки, связанные с режимом работы и условиями труда;
- регулярные выплаты на питание, жилье и топливо.
Оплата за отработанное время включает: заработную плату, начисленную по тарифным ставкам и окладам, по сдельным расценкам, в процентах от выручки за реализованную продукцию; стоимость продукции, выданной в порядке натуральной оплаты; премии и вознаграждения, носящие регулярный или периодический характер, независимо от источников их выплаты; стимулирующие доплаты и надбавки к тарифным ставкам и окладам (за профессиональное мастерство, совмещение профессии и т. п.); компенсационные выплаты и доплаты, связанные с режимом работы и условиями труда (работа во вредных или опасных условиях, работа в ночное время, сверхурочная работа и т. д.) и другие выплаты. Сюда же входит оплата труда лиц, принятых по совместительству, и оплата труда работников несписочного состава. В статистической отчетности оплата труда несписочного состава не учитывается в фонде оплаты труда списочного состава и показывается отдельно.
Оплата за неотработанное время — это различного рода выплаты, которые включают как оплату неотработанных часов в пределах рабочего дня, так и оплату неотработанных человеко-дней, в том числе: оплата ежегодных и дополнительных отпусков, оплата дополнительных отпусков, предоставленных по коллективному договору (сверх предусмотренных законодательством); оплата учебных отпусков и оплата периодов профессиональной переподготовки работников; оплата труда работников, привлекаемых к выполнению государственных и общественных обязанностей; оплата льготных часов подростков, суммы, выплаченные работникам за счет средств предприятий, вынужденно работавшим неполное время по инициативе администрации; оплата простоев не по вине работника и другие выплаты.
К единовременным поощрительным выплатам относятся единовременные (разовые) премии, вознаграждение по итогам работы за год и выслугу лет, компенсации за неиспользованный отпуск, дополнительные выплаты при предоставлении отпуска, стоимость бесплатно выдаваемых работникам в качестве поощрения'акций и другие выплаты.
Расходы на питание, жилье и топливо включают: стоимость бесплатно предоставляемых работникам отдельных отраслей экономики питания и продуктов (в соответствии с законодательством), стоимость бесплатного или по льготным ценам питания (сверх предусмотренного законодательством); стоимость бесплатно предоставляемого жилья и коммунальных услуг работникам отдельных отраслей или суммы денежной компенсации за непредоставление их бесплатно (в соответствии с законодательством), стоимость бесплатно предоставленного работникам топлива.
Фонд заработной платы исчисляется за месяц, квартал и год. Годовой фонд заработной платы равен сумме месячных фондов. Исходя из фонда заработной платы определяется уровень средней заработной платы как для предприятий и организаций, так и для отрасли и экономики в целом.
Данные о фонде заработной платы необходимы:
- для определения издержек на рабочую силу;
- для построения счета образования доходов в СНС;
- для определения валового внутреннего продукта распределительным методом.
Затраты на оплату труда являются важнейшим, а во многих отраслях экономики и самым значительным компонентом себестоимости продукции.
Фонд заработной платы на отдельных предприятиях учитывается по отдельным категориям персонала. Структура фонда заработной платы для отдельных категорий работников весьма различна, что подтверждает ее анализ как по персоналу в целом, так и по отдельным его категориям в различных отраслях экономической деятельности.
При анализе фонда заработной платы по категориям рабочих в промышленности и некоторых других сферах материального производства выделяют фонды часовой, дневной и месячной заработной платы.
Выплаты социального характера
В состав выплат социального характера, которые осуществляют предприятия и организации, включаются компенсации и социальные льготы, предоставляемые работникам на лечение, отдых, проезд, трудоустройство и другие цели.
Выплаты социального характера не включаются в заработную плату работников, но они являются составным элементом доходов лица как наемного работника, занятого на том или ином предприятии.
К выплатам социального характера относятся: надбавки к пенсиям работающим на предприятии и единовременные пособия уходящим на пенсию работникам за счет средств предприятия; страховые платежи, уплачиваемые работникам по договорам страхования за счет средств предприятия; взносы на добровольное медицинское страхование и расходы по оплате услуг организаций здравоохранения, оказываемых работникам за счет предприятия; выходные пособия при прекращении трудового договора и суммы, выплачиваемые уволенным работникам на период трудоустройства в связи с ликвидацией предприятия, сокращением штатов; оплата проезда к месту работы, разовая материальная помощь по семейным обстоятельствам; стипендии работникам, обучающимся в дневных высших и средних учебных заведениях по направлению предприятий, и другие выплаты и расходы предприятия.
Часть выплат социального характера производится на основе действующего трудового законодательства, а их значительная часть — на основе коллективных трудовых соглашений между администрацией и организациями трудящихся.
Помимо фонда заработной платы и выплат социального характера работники предприятий могут получать доходы по акциям и другие доходы от участия работников в собственности предприятий и организаций. Предприятия выплачивают страховые взносы в пенсионный фонд, фонд социального страхования и фонд обязательного медицинского страхования, государственный фонд занятости.
Важнейшие группировки, применяемые при изучении
состава оборудования.
Статистика оборудования изучает наличие, состав, состояние и использование двух групп оборудования: энергетического и производственного.
К производственному оборудованию относятся орудия труда, предназначенные для непосредственного воздействия на предмет труда в процессе производства продукции. При изучении состава производственного оборудования используются группировки по производственному и технологическому назначению, по методу воздействия на предмет труда, по степени автоматизации и др. признакам.
Энергетическое оборудование предназначено для производства различных видов энергии и преобразования одного вида энергии в другой.
Важнейшей предпосылкой интенсификации производства является улучшение использования оборудования. Для анализа эффективности использования оборудования применяется система статистических показателей, в которую входят показатели использования оборудования по численности, времени, мощности и объему работы.
Первая группа – показатели использования оборудования по численности.
Численность наличного оборудования учитывается по состоянию на определенную дату и в среднем за период. К этим показателям относятся следующие:
доля работавшего оборудования в общей численности наличного оборудования;
доля работавшего оборудования в общей численности установленного оборудования.
Вторая группа – показатели использования оборудования по времени работы.
К ним относятся:
коэффициент сменности, показывает, сколько смен в среднем работала каждая единица оборудования
в течении суток. Может быть исчислен за любой период времени: на день обследования, за месяц, квартал,
год. Общий принцип расчета заключается в сопоставлении количества отработанных оборудованием смен и
количества отработанных дней.

Чсм- общее число смен, отработанных всеми единицами оборудования за период,
Чсм- число станко-(машино-)дней , произведение среднего числа единиц оборудования и числа дней работы предприятия в этом периоде.
Поскольку один и тот же коэффициент сменности может быть у предприятий, работающих в две и в три смены, в дополнение к коэффициенту сменности исчисляется также коэффициент использования сменного режима как отношение коэффициента сменности к числу смен работы предприятия по установленному режиму.

С - число смен ; Ксм – коэфф.сменности
Этот процент означает, сколько максимально возможного числа машино-смен отрабатывалось ежедневно.
Коэффициент экстенсивной нагрузки тоже относится к показателям использования по времени.
Он исчисляется как отношение времени, фактически отработанного оборудованием, к одному из фондов времени (календарному, режимному или плановому).
Календарный фонд – число календарных часов в периоде, приходящийся на все единицы оборудования.
Режимный фонд – меньше календарного на внесменное время, праздничные и выходные дни.
Его определяют : Продолжительность смены х Число смен х Число рабочих дней х
х Число единиц оборудования
Плановый фонд – меньше режимного на время плановых ремонтов и резервное время


Коэффициент экстенсивной нагрузки показывает долю фактически отработанного времени в общем фонде времени. Разность (100% - Кэкст) отражает долю не использованного времени из-за простоев, ремонта и по др.причинам.
Третья группа – показатели использования оборудования по мощности, или коэффициенты интенсивной нагрузки оборудования. Под мощностью понимается способность оборудования производить определенную работу в единицу времени.
Эти показатели
исчисляют :

Кинт –
коэфф.интенсивной нагрузки;
 ;
;
Мmax – потенциальная мощность (т.е.плановая или паспотная).
Показывают степень использования технических возможностей оборудования в един.времени.
Разность (100% - Кинт) отражает резервы роста выпуска продукции или производства энергии в единицу времени.
Четвертая группа – коэффициенты интегральной нагрузки, которые отражают использование оборудования по объему работы. Они дают всестороннюю характеристику использования оборудования и по времени, и по мощности. Они исчисляются как отношение фактически выполненного объема работы к максимально возможному за этот период.
 Q
– объем произведенной продукции или
энергии.
Q
– объем произведенной продукции или
энергии.
Легко увидеть,
что

В качестве обобщающего показателя производственного потенциала предприятия используется – показатель производственной мощности.
Производственная мощность предприятия - это максимально возможный объем годового выпуска продукции при полном использовании производственного оборудования в условиях определенной номенклатуры продукции и режима работы предприятия. Она определяется как в натуральном так и в стоймостном выражении. Исчисляется как отношение объема фактически выпущенной продукции за год к срднегодовой производственной мощности.