Оптимизация показателей
Для вирішення задачі лінейного програмування, потрібно записати вихідну задачу в формі задачі лінейного програмування, а потім застосовувати симплекс-метод . Основною задачею лінійного програмування – задача для якої:
потрібно визначити максимальне значення ф-ції
всі обмеження записані в вигляді рівностей
для всіх змінних виконується умова невідємності
Якщо обмеження має вид нерівності зі знаком >=, то шляхом множення його на (-1) переходять до нерівності зі знаком <=.
Від обмежень нерівностей необхідно перейти до обмежень рівностей. Такий перехід виконується шляхом введення в ліву частину кожної нерівності додаткових незалежних невідємних змінних. При цьому знак нерівності міняють на знак рівності.
Вихідне завдання:
F = 5х>1>
+6х>2>
max
= 5х>1>
+6х>2>
max
 -10x>1>
- 6x>2>
-60
-10x>1>
- 6x>2>
-60
-4x>1> + 9x>2> 36
4x>1> - 2x>2> 8
x>1>,x>2>0 x>1>,x>2>-цілі числа
Основна задача:
F = 5х>1>
+6х>2>
max
= 5х>1>
+6х>2>
max
 10x>1>
+ 6x>2>
+ х>3 >=60
10x>1>
+ 6x>2>
+ х>3 >=60
-4x>1> + 9x>2> +х>4>= 36
4x>1> - 2x>2> +х>5> = 8
x>1>,x>2>,x>3>,x>4>,x>5> > >0 x>1>,x>2>-цілі числа
Кожній змінній в системі відповідає свій вектор – стовпець. Вектор – стовпець Р>о> складається із значень правих частин рівнянь і називається вектором вільних членів.
Виходячи з основного завдання, складаєм симплекс-таблицю.
|
№ рядка |
Базис |
С>б> |
Р>0> |
Р>1> |
Р>2> |
Р>3> |
Р>4> |
Р>5> |
|
1 |
Р>3> |
0 |
60 |
10 |
|
1 |
0 |
0 |
|
2 |
Р>4> |
0 |
36 |
-4 |
9 |
0 |
1 |
0 |
|
3 |
Р>5> |
0 |
8 |
4 |
-2 |
0 |
0 |
1 |
|
4 |
F |
0 |
-5 |
-6 |
0 |
0 |
0 |


Знаходження оптимального розвязку ЗЛП за допмогою с-м включає слідуючі етапи:
За вихідною с-т знаходять опорне рішення
Кожній с-т відповідає своє опорне рішення. Воно може бути представлене у вигляди вектора Х Розмірніст вектора дорівнює кількості змінних в основній задачі.
Кожній змінній в симплекс таблиці відповідає свій вектор. Змінній x>1>—вектор Р>1 >і т.д.
Вектор Р>0> складений із вільних членів рівнянь. Кожний рядок симплекс-таблиці – рівняння відповідно. Четвертий рядок—рядок оцінок в ньому записують коефіцієнти при змінних в цільовій ф-ції з протилежним знаком і визначається розв’язуємий стовпець, беруться модулі від’ємних чисел з цієї строки. В векторі Х кожній змінній відповідає певна компонента. Змінній х>1> перша компонента змінній х>2>—друга. Значення компонент визначають слідуючим чином, якщо вектор базисний, то компонента дорівнює значенню компоненти вектора стовпця Р>0 > з того рідка де в базисі стоїть 1.
У вихідній таблиці вектори Р>1>, Р>2> – не базісні, тобто в Х – перша и друга компоненти = 0
Х=(0;0;60;36;8)
Зясовують, мається хочаб одне відємне значення врядку оцінок ( рядок 4) Якщо нема – то план оптимальний, якщо є – треба переходити до новій с-т.
Рядок оцінок має (-5) та (-6), отже данний опорний план – не оптимальний.
Знаходять визначальний стовпець. Стовпець називають визначальним, якщо в рядку оцінок у нього найбільше за модулем значення. Маємо стовпець Р>2> |-6|>|-5|
Знаходимо визначальний рядок. Визанчальним назівається такий рядок, який відповідає найменшому з відношень компонентів стовпця Р>о> до додатніх компонентів визначального стовпця. (Рядок оцінок до уваги не приймається)
Min = ( 60/6; 36/9) = 4 – рядок 2.
Будують наступну с-т .
Для цього кожний елемент таблиці перераховуємо за формулою
a>ij>=a>ij>- (а>і>>k>>*> а>nj>)/a>nk> де k-номер розв’язувального стовпця, а n- номер розв’язувального рядка
a>ij>—елемент строки- і, стовпця- j нової сиплекс таблиці
a>ij>—елемент строки- і, стовпця-j попередньої симплекс-таблиці
а>і>>k>-- елемент що знаходиться у визначальному стовпці попер. с-т.
а>nj>-- елемент що знаходиться у визначальному рядку попер с-т.
a>nk> – элемент що стоїть на перехресті визн рядка и строки у попер сим-т.
a>10>= 60 – (36*6)/9 = 36
a>11>= 10 +(6*4)/9 = 38/3
|
№ рядка |
Базис |
С>б> |
Р>0> |
|
Р>2> |
Р>3> |
Р>4> |
Р>5> |
|
1 |
Р>3> |
0 |
36 |
0 |
0 |
-1 1/5 |
|
|
|
2 |
Р>2> |
6 |
4 |
-4/9 |
1 |
1 |
1/5 |
0 |
|
3 |
Р>5> |
0 |
16 |
28/9 |
0 |
0 |
3/5 |
1 |
|
4 |
F |
24 |
|
0 |
0 |
1 1/5 |
0 |
Х>1>=(0;4;36;0;16) F(X>1>) = 24
В рядку оцінок є одне відємне число. Тому Р>1> – визначальний стовпець
Min = ( 36/38*3;16/4;9) = 54/19 – визначальний рядок Р>3>
Таблиця № 3
|
№ рядка |
Базис |
С>б> |
Р>0> |
Р>1> |
Р>2> |
Р>3> |
Р>4> |
Р>5> |
|
1 |
Р>1> |
5 |
54/19 |
1 |
0 |
3/38 |
-1/19 |
0 |
|
2 |
Р>2> |
6 |
100/19 |
0 |
1 |
2/57 |
5/57 |
0 |
|
3 |
Р>5> |
0 |
136/19 |
0 |
0 |
-14/57 |
22/57 |
1 |
|
4 |
F |
870/19 |
0 |
0 |
21/38 |
5/19 |
0 |
В рядку оцінок нема відємних значень, тому даний опорний план є оптимальним. Але не виконується умова цілочисельності, тому слід застосувати відсічення по методу Гоморі.
2. Застосування і побудова відсічення по методу Гоморі
х>1>=54/19, х>2>=100/19
До системи обмежень основного завдання добавляємо ще одну нерівність виду: F(a*>ij>)*x>ij>>= F(b*>ij>), де a*>ij>> > і b*>ij> дробови частини чисел.
Під дробовою частиною числа а розуміють найменше невідємне число в і таке, що а – в є цілим числом.Якщо в оптимальному плані вихідного завдання дробового значення приймають декілька змінних, то додаткова нерівність будується для змінної, в якої найбільша дробова частина.
F(x>1>)>F(x>2>) (16/19 >5/19)
-3/38х>3>-18/19х>4> + х>6> = -16/19
таблиця № 4
|
№ рядка |
Базис |
С>б> |
Р>0> |
Р>1> |
Р>2> |
Р>3> |
Р>4> |
Р>5> |
Р>6> |
|
1 |
Р>1> |
5 |
54/19 |
1 |
0 |
3/38 |
-1/19 |
0 |
0 |
|
2 |
Р>2> |
6 |
100/19 |
0 |
1 |
2/57 |
5/57 |
0 |
0 |
|
3 |
Р>5> |
0 |
136/19 |
0 |
0 |
-14/57 |
22/19 |
1 |
0 |
|
4 |
Р>6> |
0 |
-16/19 |
0 |
0 |
-3/38 |
|
0 |
|
|
5 |
F |
870/19 |
0 |
0 |
23/38 |
5/19 |
0 |
0 |
Х>4> = ( 54/19;100/19;0;0;135/19;-16/19) F(X>4>) = 45 15/19
Т.к. опорний план містить відємну змінну то треба застосувати подвійний
с. м.
3.
Відшукання розвязку ЗЛП подвійним с-м включає слідуючі етапи:
Знахдять опорне рішення
Х>4> = ( 54/19;100/19;0;0;135/19;-16/19) F(X>4>) = 45 15/19
Перевіряють знайдений опорний розвязок на оптимальність.
Розвязок не оптимальний, тому слід перейти до нового опорного рішення.
Вибираемо визначальний рядок. Визначальним називається той, який відповідає найбільшому за модулем відємному значенню в стовпцю Р>о>
Рядок № 4
Вибираємо визначальний стовпчик. Той, який відповідає найменшему відношенню рядка оцінок до ньгого. (по модулю)
Min = (23/38*38/3;5/19*19/18) = 5/18 стовпець Р>4>
Таблиця № 5
|
№ рядка |
Базис |
С>б> |
Р>0> |
Р>1> |
Р>2> |
Р>3> |
Р>4> |
Р>5> |
Р>6> |
|
1 |
Р>1> |
5 |
26/9 |
1 |
0 |
1/12 |
0 |
0 |
-1/18 |
|
2 |
Р>2> |
6 |
140/27 |
0 |
1 |
1/36 |
0 |
0 |
5/54 |
|
3 |
Р>5> |
0 |
1048/171 |
0 |
0 |
-13/38 |
0 |
1 |
11/9 |
|
4 |
Р>4> |
0 |
8/9 |
0 |
0 |
1/12 |
1 |
0 |
-19/18 |
|
5 |
F |
410/9 |
0 |
0 |
7/12 |
0 |
0 |
5/18 |
Х>5>= (26/9;140/27;0;0;8/9;1048/171) F>5> = 45 5/9
F(x>1>) = f ( 2 8/9) = 8/9
F (x>2>) = f ( 5 5/27) = 5/27
-1/12х>3> – 17/18х>6> + х>7> = -8/9
таблица № 6
|
№ рядка |
Базис |
С>б> |
Р>0> |
Р>1> |
Р>2> |
Р>3> |
Р>4> |
Р>5> |
Р>6> |
Р>7> |
|
1 |
Р>1> |
5 |
26/9 |
1 |
0 |
1/12 |
0 |
0 |
-1/18 |
0 |
|
2 |
Р>2> |
6 |
140/27 |
0 |
1 |
1/36 |
0 |
0 |
5/54 |
0 |
|
3 |
Р>5> |
0 |
1048/171 |
0 |
0 |
-13/38 |
0 |
1 |
11/9 |
0 |
|
4 |
Р>4> |
0 |
8/9 |
0 |
0 |
1/12 |
1 |
0 |
-19/18 |
0 |
|
5 |
Р>7> |
0 |
-8/9 |
0 |
0 |
-1/12 |
0 |
0 |
|
|
|
6 |
F |
410/9 |
0 |
0 |
7/12 |
0 |
0 |
|
0 |
Таблица № 7
|
№ рядка |
Базис |
С>б> |
Р>0> |
Р>1> |
Р>2> |
Р>3> |
Р>4> |
Р>5> |
Р>6> |
Р>7> |
|
1 |
Р>1> |
5 |
50/17 |
1 |
0 |
3/34 |
0 |
0 |
0 |
-1/17 |
|
2 |
Р>2> |
6 |
260/51 |
0 |
1 |
1/57 |
0 |
0 |
0 |
5/57 |
|
3 |
Р>5> |
0 |
1608/323 |
0 |
0 |
-436/969 |
0 |
1 |
0 |
11/17 |
|
4 |
Р>4> |
0 |
32/17 |
0 |
0 |
3/17 |
1 |
0 |
0 |
-19/17 |
|
5 |
Р>6> |
0 |
16/17 |
0 |
0 |
3/34 |
0 |
0 |
1 |
-18/17 |
|
6 |
F |
770/17 |
0 |
0 |
19/34 |
0 |
0 |
0 |
5/17 |
Х>6>= ( 50/17;260/51;0;32/17;1608/323;16/17) F>6> = 45 5/17
Будуємо нове відсічення:
F(x>1>) = f(2 16/17) = f(16/17) = 16/17
F(x>2>) = f (5 5/51) = f(5/51) = 5/51
F(x>1>)> F(x>2>)
-3/34x>3> – 16/17x>7> + x>8> = -16/17
таблица №8
|
№ рядка |
Базис |
С>б> |
Р>0> |
Р>1> |
Р>2> |
Р>3> |
Р>4> |
Р>5> |
Р>6> |
Р>7> |
Р>8> |
|
1 |
Р>1> |
5 |
50/17 |
1 |
0 |
3/34 |
0 |
0 |
0 |
-1/17 |
0 |
|
2 |
Р>2> |
6 |
260/51 |
0 |
1 |
1/57 |
0 |
0 |
0 |
5/57 |
0 |
|
3 |
Р>5> |
0 |
1608/323 |
0 |
0 |
-436/969 |
0 |
1 |
0 |
22/17 |
0 |
|
4 |
Р>4> |
0 |
32/17 |
0 |
0 |
3/17 |
1 |
0 |
0 |
-19/17 |
0 |
|
5 |
Р>6> |
6 |
16/17 |
0 |
0 |
3/34 |
0 |
0 |
1 |
-18/17 |
0 |
|
6 |
Р>8> |
0 |
-16/17 |
0 |
0 |
-3/34 |
0 |
0 |
0 |
|
1 |
|
7 |
F |
770/17 |
0 |
0 |
19/34 |
0 |
0 |
0 |
5/17 |
0 |
Таблица №9
|
№ рядка |
Базис |
С>б> |
Р>0> |
Р>1> |
Р>2> |
Р>3> |
Р>4> |
Р>5> |
Р>6> |
Р>7> |
Р>8> |
|
1 |
Р>1> |
5 |
3 |
1 |
0 |
3/32 |
0 |
0 |
0 |
0 |
0 |
|
2 |
Р>2> |
6 |
5 |
0 |
1 |
1/96 |
0 |
0 |
0 |
0 |
0 |
|
3 |
Р>5> |
0 |
70/19 |
0 |
0 |
-521/912 |
0 |
1 |
0 |
0 |
0 |
|
4 |
Р>4> |
0 |
3 |
0 |
0 |
9/32 |
1 |
0 |
0 |
0 |
0 |
|
5 |
Р>6> |
0 |
2 |
0 |
0 |
3/16 |
0 |
0 |
1 |
0 |
0 |
|
6 |
Р>7> |
0 |
1 |
0 |
0 |
3/32 |
0 |
0 |
0 |
1 |
1 |
|
7 |
F |
45 |
0 |
0 |
17/32 |
0 |
0 |
0 |
0 |
0 |
Х*=(3; 5) F*=45
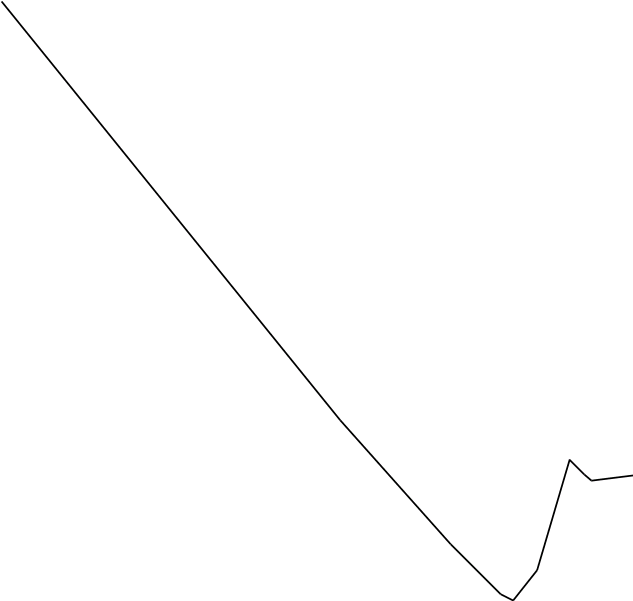
4. Геометирчна интерпретація процесу розвязку.
Геометирчна интерпретація процесу розвязку дозволяє наглядно проілюстровати процесс знаходження оптимального плану.
Будують прямі, рівняння яких отримують в результаті заміни в обмеженнях знаків нерівностей на знаки =.
 10x>1>
+ 6x>2>
=60 (1)
10x>1>
+ 6x>2>
=60 (1)
-4x>1> + 9x>2> = 36 (2)
4x>1> - 2x>2> = 8 (3)
x>1>=0, (4)
x>2>=0 (5)
Графіком рівняння x>1 >= 0 є вісь ординат, x>2 >=0 – вісь абсцисс.
Графіки решти рівнянь будують так. Оскільки графіки – це прями, то достатньо для кожного рівняння знайти дві точки, задовільнюючі йому, і через них провести пряумю.
Визначають область допустимих значень.
Область допустимих значень знаходиться в перший чверті координат, т.к. x>1>,x>2>0 x>1>,x>2>-цілі числа
На коорд. Площині вибирають довільну точку і перевіряють виконання тотожністів рівняннях-обмеженнях. Якщо тотожність вірна, то дана нпівплощина – площина напівплощина допустимих рішень.
Будують радіус-вектор.
 10
10






 М
М

















 4
4









(2)
6
-9
(3)
(1)
-4

 10
10







 В М
В М

















 4
4








( I )
-38/3
(2)
6

-9
(3)
(1)
-4
В точці В, що є оптимальною за даних умов, перетикаються (I) відсічення та (1) обмеження. Знайдемо координати т.В
-3х>1> + 9х>2> = 38 х>1>=26/9
т.В (26/9; 140/27)
10х>1>+ 6х>2> = 60 х>2>=140/27 F ( B) = 45 5/9
-1/12х>3> – 17/18х>6> = -8/9 – второе отсечение.
-1/12х>3>*(60 – 10х>1>- 6х>2>) – 17/18*(38 + 3х>1> – 9х>2>) = -8/9
-2х>1> + 9х>2> = 40 – уравнение 2-го отсечения.
Х>7>= 40 + 2х>1> - 9>2>

 10
10








 В М
В М
















 С
С
 4
4









(
-38/3
II ) (I)(2)
6

-9
2 16/17
-20 (II) (3)
(1)
-4

 10
10









 В М
В М
















 С
С
D
 4
4
(






 III)
III)

( II ) (I)
(2)
6

-9
2 16/17
-20 (II) (3)
(1)
-4
Уравнение третьего отсечения:
-3/34х>3> – 16/17х>7> = -16/17
х>7> находится из 2 го ограничения
-3/34 * ( 60 – 10х>1> – 6х>2>) – 16/17*(40 + 2х>1> – 9х>2>) = -16/17
-х>1> + 9х>2> = 42 – ур. Третьего отсечения
В т. D пересекаются (1) и (III)
1 0х>1>
+ 6х>2> = 60
0х>1>
+ 6х>2> = 60
-х>1> + 9х>2> = 42
х>1>=3; х>2>=5. F(D)=45
т.D (3;5)
Вывод:
экономико-матем. модел. испольузется в экономике для решения различного рода заданий, для оптимизации их. В данной к.р. использованы симплекс метод,….. отсечения Гомори, двойной симплекс метод. Геометрическая интерпретация показывает весь ход решения.
Список використаної літератури:
Кузнецов Ю.Н. “Математическое програмирование:(учебное пособие для экономических специальностей ”
Оптимізація єкономічних показників з врахуванням умови цілочисленності: “Методичні вказівки до виконання курсової роботи з дисципліни “Економіко математичне моделювання для студентів економічних спеціальностей”(Викладач Іванов Л.П. –Чернігів: ЧТІ,1998-20с)”
1
 6
6 Р>1>
Р>1> 0
0 -23/3
-23/3 -18/19
-18/19 1
1 -17/18
-17/18 -16/17
-16/17