Модель прогнозирования параметров финансовых рынков и оптимального управления инвестиционными портфелями
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
МОДЕЛЬ ПРОГНОЗИРОВАНИЯ ПАРАМЕТРОВ ФИНАНСОВЫХ РЫНКОВ И ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ИНВЕСТИЦИОННЫМ ПОРТФЕЛЕМ.
Выполнил:
Проверил:
г.Пермь 2000.
Построение математической модели прогнозирования поведения является трудной задачей в связи с сильным влиянием политических и других проблем (выборы, природные катаклизмы, спекуляции крупных участников рынка…).
В основе модели лежит анализ некоторых критериев с последующим выводом о поведении доходности и ценовых показателей. В набор критериев входят различные макро- и микроэкономические показатели, информация с торговых площадок, экспертные оценки специалистов. Процедура прогнозирования состоит из этапов:
Подготовка и предварительная фильтрация данных;
Аппроксимация искомой зависимости линейной функцией;
Моделирование погрешности с помощью линейной сети.
Но для повышения точности модели практикуется нелинейный анализ с использованием многослойной однородной нейронной сети. Этапы проведения нелинейного анализа в системе совпадают со стандартными шагами при работе с нейросетями.
1-й этап. Подготовка выходных данных.
Выходными данными являются z>i >= y>i>-p>i>, где y>i> - реальное значение прогнозируемой величины на некоторую дату, p>i> - рассчитанное на эту дату с помощью линейного анализа.
2-й этап. Нормирование входных сигналов.
 (1)
(1)
где x>i>j - j-я координата некоторого критерия X>i>, M[X>i>] - выборочная оценка среднего квадратичного отклонения.
3-й этап. Выбор функции активации и архитектуры нейронной сети.
Используются функции активации стандартного вида (сигмоидная, ступенчатая), а также следующего вида:
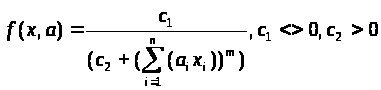 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
Архитектура нейронной сети представлена на рисунке:
>1>
f>1>
вектор
в

 ходных
ходных
с
игналов вектор 
выходн.
В
>m>
f>1>
 ектор сигналов
ектор сигналов
в
 ходных
ходных
сигналов
Введены следующие обозначения: >j> - линейные сумматоры; f>j> - нелинейные функции; используемые для аппроксимации; - итоговый сумматор.
4-й этап. Выбор алгоритма обучения нейронной сети, основанного на одном из следующих методов: обратного распространения ошибки, градиентного спуска, метода сопряженных градиентов, методе Ньютона, квазиньютоновском. Методы оцениваются по времени, затрачиваемому на обучение и по величине погрешности.
5-й этап. Итоговые вычисления границ прогнозируемого значения:
P=P>лин>+Р>нелин>Е>нелин>
где Р — итоговое прогнозируемое значение, Р>лин> и Р>нелин> значение линейного и нелинейного анализов. Е>нелин> — погрешность полученная на этапе нелинейного анализа.
Результаты задачи прогнозирования используются в построенной на ее основе задаче оптимального управления инвестиционным портфелем. В основе разработанной задачи управления идея минимизации трансакционных издержек по переводу портфеля в класс оптимальных.
Используемый поход основан на предположениях, что эффективность инвестирования в некий набор активов является реализацией многомерной случайной величины, математическое ожидание которой характеризует доходность (m={m>i>}>i=1..n>, где m>i>=M[R>i>], i=1..n), матрица ковариаций — риск (V=(V>ij>), i,j=1..n, где V>ij>=M[(R>i>-m>i>)(R>j>-m>j>)],i,j=1..n). Описанные параметры (m,V) представляют собой оценку рынка и являются либо прогнозируемой величиной, либо задаются экспертно. Каждому вектору Х, описывающему относительное распределение средств в портфеле, можно поставить в соответствие пару оценок: m>x>=(m,x), V>x>=(Vx,x). Величина m>x> представляет собой средневзвешенную доходность портфеля, распределение средств в котором описывается вектором Х величина Vх (вариация портфеля [3,5]) является количественной характеристикой риска портфеля х. Введем в рассмотрение оператор Q, действующий из пространства Rn в пространство R2 (критериальная плоскость [3]), который ставит в соответствие вектору х пару чисел (m>x>, V>x>):
Q: Rn-R2 xRn, x((m,x),(Vx,x)). (7)
В задаче управления допустимыми считаются только стандартные портфели, т.е. так называемые портфели без коротких позиций. Правда это накладывает на вектор х два ограничения: нормирующее условие (е,х)=1, где е – единичный вектор размерности n, и условие неотрицательности доли в портфеле, х>=0. Точки удовлетворяющие этим условиям образуют dв пространствеRn так называемый стандартный (n-1)-мерный симплекс. Обозначим его .
={xRn(e,x)=1, x0}
Образом симплекса в критериальной плоскости будет являться замкнутое ограниченное множество оценок допустимых портфелей. Нижняя граница этого множества представляет собой выпуклую вниз кривую, которая характеризует Парето – эффективный с точки зрения критериев выбор инвестора (эффективная граница [3], [5]). Прообразом эффективной границы в пространстве Rn будет эффективное множество портфелей [5]. Обозначим его как . Данное множество является выпуклым: линейная комбинация эффективных портфелей также представляет собой эффективный портфель [3].
Пусть в некоторый момент времени у нас имеется портфель, распределение средств в котором описывается вектором х. Тогда задачу управления можно сформулировать в следующем виде: найти такой элемент y, принадлежащий , что (y,x). Иными словами, для заданной точки х требуется найти ближайший элемент y, принадлежащий множеству . В пространстве Rn справедлива теорема, доказывающая существование и единственность элемента наилучшего приближения х элементами множества [6]. Метрика (понятие расстояния) может быть введена следующим образом:
(x,y)=>i=1,n>sup(y>i>-x>i>,0)+>i=1..n>sup(x>i>-y>i>,0), (9)
где >0 — относительная величина издержек при покупке, >0 — относительная величина издержек при продаже актива.
Литература
Сборник статей к 30-ти летию кафедры ЭК. ПГУ.
Ивлиев СВ Модель прогнозирования рынка ценных бумаг. 6-я Всероссийская студенческая конференция «Актуальные проблемы экономики России»: Сб.тез.докл. Воронеж, 2000.
Ивлиев СВ Модель оптимального управления портфелем ценных бумаг. Там же.