Наращение денег по простым процентам
Задачи на простые проценты
Банк концерна "А" с целью сказания финансовой помощи выдал ссуду 10 млн. руб. дочернему предприятию под 20% годовых сроком на 3 года. Проценты простые. Определить сумму возврата ссуды и доход банка.
Решение:
Сумма наращения денег по простым процентам
S = P (1 + ni),
где P - сумма кредита;
n - срок кредита, лет;
i - процентная ставка.
Таким образом, сумма возврата ссуды составит:
S = 10 (1 + 3*0,2) = 16 млн. руб.
Доход банка - разность между суммой выдачи и суммой возврата (т.е. величина процентов по ссуде):
16 - 10 = 6 млн. руб.
Определить проценты и сумму накопленного долга, если ссуда равна 7 млн. руб., срок долга - 4 года по ставке простого процента, равной 10% годовых.
Решение:
Сумма наращения денег по простым процентам
S = P (1 + ni),
где P - сумма кредита;
n - срок кредита, лет;
i - процентная ставка.
Таким образом, сумма накопленного долга составит
S = 7 (1 + 0,1*4) = 9,8 млн. руб.
Сумма процентов
J = S - P = 9,8 - 7 = 2,8 млн. руб.
Ссуда в размере 100 тыс. руб. выдана 20 января до 5 октября включительно под 8% годовых, год невисокосный. Необходимо найти размер погасительного платежа, применяя три метода нахождения продолжительности ссуды (см. приложение). Решение:
Точное число дней ссуды получим по Приложению:
278 - 19 = 259 дней
Приближенное число дней ссуды (продолжительность каждого месяца 30 дней):
11 + 30 + 30 + 30 + 30 + 30 + 30 + 30 + 30 + 5 = 256 дней
Возможные варианты расчета наращенной суммы:
а) по точным процентам с точным числом дней ссуды:
 = 105,67 тыс. руб.
= 105,67 тыс. руб.
б) по обыкновенным процентам с точным числом дней ссуды:
 = 105,75 тыс. руб.
= 105,75 тыс. руб.
в) по обыкновенным процентам с приближенным числом дней ссуды:
 = 105,69 тыс. руб.
= 105,69 тыс. руб.
Контракт предусматривает следующий порядок начисления процентов: первый год-25%, в каждом последующем полугодии ставка повышается на 11%. Необходимо определить множитель наращения за 2.5 года.
Решение:
При установлении переменной процентной ставки наращенная сумма определяется по формуле:

Выражение в скобках и представляет собой множитель наращения. Рассчитаем его:
1 + 1*0,25 + 0,5*0,36 + 0,5*0,47 + 0,5*0,58 = 1,955
Таким образом, по данному контракту наращенная сумма будет в 1,955 раза больше первоначальной.
На сумму 10 млн. руб. начисляется 10% годовых. Проценты простые, точные. Какова наращенная сумма, если операция реинвестирования проводится ежемесячно в течение первого квартала, и какова наращенная сумма, если операция реинвестирования не проводится?
Решение:
Иногда прибегают к начислению процентов на уже наращенные в предыдущем периоде суммы, т.е. происходит многоразовое наращение, именуемое реинвестированием, или капитализацией процентного дохода. В этом случае итоговая наращенная сумма определится по формуле:

В нашем случае наращенная сумма за квартал составит:
S = 10* (1 + (30/365) *0,1) * (1 + (30/365) *0,1) * (1 + (30/365) *0,1) = 10,249 млн. руб.
Если операция реинвестирования не производится, то наращенная сумма составит:
S = 10* (1 + (90/365) *0,1) = 10,246 млн. руб.
Задачи на сложные проценты.
Вкладчик внес 2 млн. руб. в банк под 50% годовых на 5 лет. Проценты сложные. Какая сумма средств вкладчика по окончании срока? Чему равен доход вкладчика за 5 лет?
Решение:
Наращенная сумма денег по формуле сложных процентов имеет вид
S = P (1 + i) n,
где P - сумма кредита;
n - срок кредита, лет;
i - процентная ставка.
Таким образом, сумма средств вкладчика по окончании срока
S = 2 (1 + 0,5) 5 = 15,1875 млн. руб.
Доход вкладчика
J = S - P = 15,1875 - 2 = 13,1875 млн. руб.
Банк взимает за ссуду 40% годовых. За второй год установления банком маржа составляет 2%, за каждый последующий год 3%. Срок ссуды-5 лет. Размер ссуды-5 млн. руб. Найти сумму возврата долга через 5 лет.
Решение:
Нестабильность экономической ситуации вынуждает банки использовать в кредитных сделках изменяющиеся во времени, но заранее фиксированные для каждого периода ставки сложных процентов. В этом случае наращенная сумма может быть определена по формуле:

Таким образом, сумма возврата через 5 лет составит:
S = 5* (1 + 0,4) * (1 + 0,42) * (1 + 0,43) 3 = 29 млн. руб.
Первоначальная сумма ссуды-10 тыс. руб., срок-5 лет, проценты начисляются в конце каждого квартала, номинальная годовая ставка-5%. Требуется определить наращенную сумму. Решение:
Так как проценты начисляются поквартально, используем формулу сложных процентов с разовым начислением по номинальной ставке
 ,
,
где j - номинальная ставка;
m - число периодов начисления в году;
n - число лет финансовых вложений.
Тогда наращенная сумма составит
 = 12,820372 тыс. руб.
= 12,820372 тыс. руб.
Банк начисляет проценты по номинальной ставке 40% годовых. Найти, чему равна эффективная годовая ставка при ежемесячном начислении процентов.
Решение:
Зависимость эффективной и номинальной процентных ставок выглядит следующим образом:
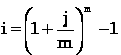
Тогда эффективная ставка составит
 = 0,482 = 48,2%
= 0,482 = 48,2%
Простая процентная ставка по векселю равна 10%. Определить значение эквивалентной учетной ставки, если вексель выдан: а) на 2 года; б) на 250 дней. При сроке долгового обязательства 250 дней временную базу ставок примем равной 360 дням.
Решение:
Эквивалентная учетная ставка связана с простой учетной ставкой следующей зависимостью:
 ,
,
где i - простая учетная ставка;
n - срок ссуды в годах.
В случае, когда срок ссуды меньше года:
n = t/K,
где t - число дней ссуды;
К = 360 дней.
Определим эквивалентную учетную ставку, если вексель выдан на 2 года:
 =
8,33%
=
8,33%
Как видно, при наращении по учетной ставке 8,33% владелец векселя получит такой же доход, что и по простой ставке 10%.
Определим эквивалентную учетную ставку для векселя, выданного на 250 дней:
 =
9,35%
=
9,35%
Определить процентную ставку, эквивалентную учетной, равной 30%, если наращение определяется: а) по простым процентам; б) по сложным процентам. Срок погашения-2 года.
Решение:
В случае простых процентов простая ставка, эквивалентная учетной, определяется по следующей формуле:

Соответственно, простая ставка, эквивалентная учетной ставке в 30%, будет:
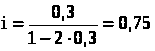 =
75%
=
75%
В случае сложных процентов ставка, эквивалентная учетной, определяется по формуле:

Соответственно, при сложной учетной ставке в 30% эквивалентная ей сложная ставка составит
 =
42,85%
=
42,85%
Задачи по дисконтированию.
Через год владелец векселя, выданного коммерческим банком, должен получить по нему 220 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если годовая ставка составляет 120%?
Решение:
Используем формулу математического дисконтирования

Таким образом, первоначальная сумма составит
 тыс. руб.
тыс. руб.
Фирма планирует кредит в сумме 10 млн. руб. при ставке 200% годовых. Каким должен быть срок ссуды, чтобы сумма возврата долга составила не более 20 млн. руб?
Решение:
Очевидно, что срок ссуды будет менее года, поэтому для определения срока ссуды в днях воспользуемся формулой:
 ,
,
где К = 360 дней.
 дней
дней
Если фирма хочет выплатить не более 20 млн. руб., она должна взять ссуду на 180 дней, т.е. на полгода.
Предприниматель обратился в банк за ссудой в размере 200 тыс. руб. на срок 55 дней. Банк согласился выдать указанную сумму при условии начисления процентов по простой учетной ставке, равной 80%. Чему равна сумма долга, указанная в векселе?
Решение:
Если срок ссуды определяется в днях для простой учетной ставки, наращенная сумма будет равна:
 ,
,
где t - срок ссуды в днях;
d - простая учетная ставка;
К = 360 дней.
Тогда сумма долга, указанная в векселе, составит:
 228
тыс. руб.
228
тыс. руб.
Фирме необходим кредит в 500 тыс. руб. Банк согласен на выдачу кредита при условии, что он будет возмещен в размере 600 тыс. руб. Учетная ставка-210% годовых. На какой срок банк предоставит кредит фирме (К=365 дней)?
Решение:
Для определения срока кредита в днях воспользуемся формулой

Срок кредита составит
 дня
дня
Контракт на получение ссуды на 500 млн. руб. предусматривает возврат долга через 30 дней в сумме 600 тыс. руб. Определить примененную банком учетную ставку (К=365 дней).
Решение:
Учетная ставка определяется по формуле:

