Проектирование операционного устройства
ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра «Электронные вычислительные машины»
Курсовой проект
по дисциплине «Теория автоматов»
Проектирование операционного устройства.
Выполнил
ст. гр. ИНФО-810
Бабкин А. Н.
Проверил
Ефимова Р. С.
САНКТ-ПЕТЕРБУРГ
2000
В вычислительной технике применяются так называемые операционные устройства. Эти устройства могут выполнять различные операции над кодовыми словами. Любая операция может быть представлена конечной последовательностью действий, эти действия называются микрооперациями.
В данной работе проводится проектирование операционного устройства, выполняющего операцию сложения двоичных чисел с фиксированной запятой в обратных кодах.
Содержание
Введение.________________________________________________________________4
Разработка структурной схемы операционного автомата.
Разработка содержательного графа операции
сложения двоичных чисел в обратных кодах._____________________________5
Разработка структурной схемы операционного автомата.__________________8
Разработка функциональной схемы операционного автомата.
Синтез блока П._____________________________________________________10
Синтез блока C._____________________________________________________11
Разработка функциональной схемы управляющего автомата.
Структурная схема управляющего автомата._____________________________28
Закодированная граф-схема работы управляющего
автомата и граф управляющего автомата.________________________________28
Синтез комбинационных схем, реализующих функции возбуждения
элементов памяти управляющего автомата.______________________________31
Функциональная схема операционного устройства.
Организация связей между ___________________________________________33
операционным и управляющим автоматами.
Описание работы операционного устройства
на заданном отрезке времени.__________________________________________33
Заключение.______________________________________________________________34
Литература.______________________________________________________________34
Приложение._____________________________________________________________35
Введение
Задачей данного курсового проекта является разработка операционного устройства для выполнения заданной операции сложения с фиксированной запятой чисел, представленных обратными двоичными кодами
на уровне логических схем. Эта задача разбивается на две: разработку схем операционного автомата и управляющего автомата.
Все непосредственные операции действий над словами, вычисления логических условий, хранения данных возлагаются на операционный автомат.
Управляющий автомат вырабатывает последовательность управляющих сигналов в соответствии микропрограммой функционирования операционного устройства. Эти управляющие сигналы поступают на вход операционного устройства.
OУ
HO
F>i>
И
Y>N>
X>1>
Y>1>
УА
ОА
Р
Р
X>N>
.
Разработка структурной схемы операционного автомата
1.1. Разработка содержательного графа операции сложения двоичных чисел в обратных кодах
Для составления формального описания работы операционного устройства (ОУ) необходимо проанализировать словесное описание алгоритма выполнения заданной операции и с учетом исходных данных дать описание с помощью Ф-языка:
слов (наименование, тип, формат);
микроопераций;
логических условий;
Описание слов показано в табл. 1.
Таблица 1
|
Слово |
Назначение слова |
Тип слова |
|
А(1:25) |
Первое слагаемое |
Входное, внутреннее |
|
В(1:25) |
Второе слагаемое |
Входное, внутреннее |
|
С(1:26) |
Результат |
Внутреннее, выходное |
|
П(1) |
Признак переполнения |
Внутреннее, выходное |
Описание микроопераций дано в табл. 2.
Таблица 2
|
Пункт алгоритма |
Словесное описание |
Условное обозначение |
Формальное описание |
|
1 |
Начало |
y>0> |
|
|
2 |
Присвоение слову П(1) и старшему разряду слова С(1:26) значение нуля |
y>1> |
П(1):=0 С(1):=0 |
|
3 |
|||
|
4.1 |
Слову С(1:26) присвоить значение суммы слов В(1:25) и А(1:25) с инверсией числовых разрядов последнего |
y>2> |
C(1:26):=00.В(2:25)+01.А(2:25) |
|
5.1 |
Слову С(1:26) присвоить значение суммы слов А(1:25) и В(1:25) с инверсией числовых разрядов последнего |
y>3> |
C(1:26):=00. А(2:25) + 01.В(2:25) |
|
6.1 |
К слову С(1:26) прибавить единицу младшего разряда |
y>4> |
С(1:26):= С(1:26)+1 |
|
7.1 |
Образование в С(1:26) прямого кода результата |
y>5> |
С(1:26):= С(1:2).С(3:26) |
|
8 |
Слову С(1:26) присвоить значение суммы слов А(1:25) и В(1:25) |
y>6> |
C(1:26):=00. А(2:25) + 00.В(2:25) |
|
9.1 |
Слову П(1) присваивается значение единицы |
y>7> |
П(1):=1 |
|
9.2 |
Знаковому разряду слова С(1:26) присвоить значение знакового разряда слова А(1:25) |
y>8> |
С(2):=А(1) |
|
10 |
Конец |
y>0> |
Логические условия, под действием которых вырабатываются управляющие сигналы, описаны в табл. 3.
Таблица 3
|
Пункт алгоритма |
Словесное описание логических условий |
Условное обозначение |
Формальное описание |
|
3 |
Проверка знака слова А(1:25) |
x>1> |
|
|
4,5 |
Проверка знака слова В(1:25) |
x>2> |
|
|
6 |
Проверка старшего разряда слова С(1:26) |
x>3> |
|
|
7,9 |
Проверка знака слова С(1:26) |
x>4> |
|
Для проектирования ОУ необходимо удостоверится в правильности алгоритма, для этого "прогонка" (проверка) алгоритма проводилась по всем возможным случаям знака множителей, а также на случай переполнения. В результате этой проверки выяснено, что алгоритм верен, и на его основе можно ОУ (см. Приложение табл. 20).
Чтобы связи между ступенями алгоритма представлялись яснее, весь алгоритм можно изобразить в виде содержательного графа, который дает визуальное представление об алгоритме данной операции. Содержательный граф-схема микрооперации предсталена на рис. 1.1.1.
начало
П(1):=0
С(1):=0
А(1)
В(1)
В(1)
С(2)
С(1)
С(1)
0
0
1
0
0
0
1
1
1
1
1
0
конец
C(1:26):=00.В(2:25)+01.А(2:25)
C(1:26):=00. А(2:25) + 01.В(2:25)
С(1:26):= С(1:2).С(3:26)
С(2):=А(1)
П(1):=1
C(1:26):=00. А(2:25) + 00.В(2:25)
С(1:26):= С(1:26)+1
В структурном отношении операционный автомат может быть разбит на блоки, каждый из которых содержит в себе элементы памяти и комбинационные схемы, количество блоков определяется количеством слов с памятью.
Память – это регистр, длина которого совпадает с длиной слова.
Если микрооперации выполняются над отдельными разрядами слова и при этом различны в разных разрядах, то в регистре выделяются так называемые поля, то есть совокупности разрядов объединенных общей совокупностью микроопераций или общим участием в формировании условий. Например, поле знаковых разрядов.
Разбиение на поля данных слов при заданной операции описано в табл. 4.
Таблица 4
|
Имя блока |
Множество микроопераций в блоке |
Множество логических условий |
Поля |
|
А |
x>1> |
А(1), А(2:25) |
|
|
В |
x>2> |
В(1), В(2:25) |
|
|
С |
y>1>, y>2>, y>3>, y>4>, y>5>, y>6>, y>8> |
x>3>, x>4> |
С(1), С(2), С(3:25), С(26) |
|
П |
y>1>, y>7> |
П(1) |
1.2 Разработка структурной схемы операционного автомата.
Структурная схема дает представление о количестве блоков, входящих в структуру, их назначении, описание особенностей и о связях между блоками в процессе реализации функций устройства.
Количество блоков равно количеству слов с памятью, то есть необходимо четыре блока.
Связь между блоками (регистрами) осуществляется при передаче информации из блока в блок или при занесении информации извне.
Входными сигналами в операционный автомат являются сигналы из управляющего автомата, они дают команду на выполнение микроопераций над словами. Выходными сигналами из операционного автомата являются значения логических условий, которые в свою очередь поступают на входы управляющего автомата.
Тогда с помощью данных из таблиц 1, 2, 3, 4 можно составить структурную схему операционного автомата, которая представлена на рис. 1.2.1.
x>1>
1
2
Блок А
25
x>2>
1
2
Блок В
25
y>2>
y>3>
y>6>
y>8>
x>3>
x>4>
1
2
3
Блок С
25
26
y>1>
y>4>
y>5>
Блок П
y>7>
Рис. 1.2.1.
2. Разработка функциональной схемы операционного автомата
2.1. Синтез блока П
Для синтеза комбинационной схемы каждого разряда необходимо четко знать какие микрооперации выполняются в блоке, какие логические условия вычисляются в нем и какие поля выделены. Это видно из таблицы 4.
Тогда можно приступать к синтезу комбинационной схемы разрядов каждого поля, но так как разряды каждого поля обрабатываются одинаково, то можно синтезировать только один разряд из соответствующего поля.
Синтез поля П(1).
Над этим полем выполняются несколько микроопераций, поэтому синтез осуществляется на каждом поле отдельно, а потом эти результаты объединяются. То есть будут составляться функции возбуждения триггера для каждой микрооперации, а далее эти функции объединяются в функцию окончательного результата путем выполнения операции дизъюнкции функций возбуждения, полученных для каждой микрооперации. Это возможно, так как над одним и тем же полем одновременно может выполняться только одна микрооперация. Все эти условия распространяются и на все другие поля всех блоков.
y>1>>:>
П(1):=0
Можно составить каноническую таблицу переходов автомата (табл. 5).
Табл. 5
|
>t> |
>t+1> |
>t> |
|
|
>П(1)> |
>П(1)> |
>J> |
>K> |
|
>0> |
>0> |
>0> |
>0>>>>1> |
|
>1> |
>0> |
>0>>>>1> |
>1> |
Из табл. 5 можно написать функцию возбуждения для триггера по входам J и K.
J=0,
K=1.
y>7>>:>
П(1):=1
Можно составить каноническую таблицу переходов автомата (табл. 6).
Табл. 6
|
>t> |
>t+1> |
>t> |
|
|
>П(1)> |
>П(1)> |
>J> |
>K> |
|
>0> |
>1> |
>1> |
>0>>>>1> |
|
>1> |
>1> |
>0>>>>1> |
>0> |
Из табл. 6 можно написать функцию возбуждения для триггера по входам J и K.
J=1,
K=0.
Теперь можно написать общий вид функции возбуждения поля П(1).
Логическая схема поля П(1) будет выглядеть так, как показано на рис. 2.1.1.
J
C
K
Т
y>7>
П(1)
y>1>
синхр
Рис. 2.1.1.
2.2. Синтез блока С
В блоке С выделено несколько полей, соответственно синтез будет производиться для каждого из них отдельно.
Поле С(1).
y>1>>:>
С(1):=0
Таблица и функции аналогичны таблице 5 и функциям для микрооперации y>1> над полем П(1).
J=0, K=1.
y>2>:
С(1):=P(1), где P(1) – перенос в первый разряд из второго.
Так как р поле С(1) было обнулено при микрооперации y>1>, то в таблице 7 можно рассматривать только наборы, где С(1)=0.
Таблица 7
|
t |
t+1 |
t |
||
|
С(1) |
P(1) |
С(1) |
J |
K |
|
0 |
0 |
0 |
0 |
01 |
|
0 |
1 |
1 |
01 |
1 |
Дополнив функцию на невозможных наборах, получаются следующие выражения функций возбуждения.
J=P(1),
K=1.
Функция P(1) будет найдена при синтезе поля С(2), так как она зависит от значения самого поля, переноса в этот разряд и значения слагаемых, сумма которых записывается в разряд С(2).
y>3>:
В этой микрооперации все аналогично таблице 7, то есть
J=P(1), K=1.
y>6>:
С(1):=0
Таблица переходов аналогична таблице 5, значит сразу известны выражения для J и K.
J=0, K=1.
y>4>:
C(1):=C(1)+P(1)
J=P(1)
K=P(1)
Окончательный результат синтеза поля С(1) может быть представлен в виде:
Логическое условие:
x>3>=С(1).
Логическая схема поля С(1) будет выглядеть так, как это показано на рис. 2.2.1.
1
y>2>
y>3>
&
y>4>
P(1)
J
C
K
Т
С(1)
y>1>
y>2>
y>3>
1
1
y>4>
&
синхр
P(1)
Рис. 2.2.1.
Данной схеме можно сопоставить условное изображение "черного ящика", то есть известно, что на входе и, что на выходе. Эта схема представлена на рисунке 2.2.2.
P(1)
y>1>
y>2>
y>3>
y>4>
y>6>
С
С(1)
С(1)
Рис. 2.2.2.
Поле С(2).
y>2>:
С(2):=1+P(2)
Можно перейти к булеву выражению этого разряда
С(2)=
Соответственно таблица функций (табл. 8) возбуждения будет выглядеть так:
Таблица 8
|
T |
t+1 |
t |
|||
|
С(2) |
P(2) |
С(2) |
P(1) |
J |
K |
|
0 |
0 |
1 |
0 |
1 |
01 |
|
0 |
1 |
0 |
1 |
0 |
01 |
|
1 |
0 |
1 |
0 |
01 |
0 |
|
1 |
1 |
0 |
1 |
01 |
1 |
Из данной канонической таблицы необходимо написать выражения функций J, K, P(1).
y>3>:
Абсолютно аналогично y>2>:
y>6>:
С(2):=P(2)
Соответственно таблица функций (табл. 9) возбуждения будет выглядеть так:
Таблица 9
|
T |
t+1 |
t |
|||
|
С(2) |
P(2) |
С(2) |
P(1) |
J |
K |
|
0 |
0 |
0 |
0 |
0 |
01 |
|
0 |
1 |
1 |
0 |
1 |
01 |
|
1 |
0 |
0 |
0 |
01 |
1 |
|
1 |
1 |
1 |
0 |
01 |
0 |
Из данной канонической таблицы необходимо написать выражения функций J, K, P(1).
y>8>:
С(2):=А(1)
Таблица аналогична таблице 9, только столбец P(2) заменяется на А(1). А функции выглядят так:
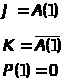
y>4>:
C(2):=C(2)+P(2)
J=P(2)
K=P(2)
P(1)=P(2)C(2)
Составляются результирующие функции возбуждения элемента памяти и переноса в старший разряд, а также выражение функции логического условия.
Выражение для P(2) будет найдено при синтезе поля С(3:25).
Л
y>2>
огическая схема для С(2) выглядит как показано на рис. 2.2.3.
1
&
y>3>
1
P(2)
1
J
C
K
&
y>4>
y>6>
A(1)
Т
&
С(2)
y>8>
&
y>4>
&
1
y>6>
1
&
синхр
y>8>
Рис. 2.2.3.
На рис. 2.2.4. представлено условное обозначение разряда С(2).
Рис. 2.2.4.
Л
y>2>
огическая
схема переноса в С(1) представлена на
рис. 2.2.5.
1
&
P(2)
P(1)
&
y>4>
C(2)
y>3>
Рис. 2.2.5.
Поле С(3:25).
Здесь для синтеза можно выбрать любой разряд этого поля, и обозначить его как С(i).
y>2>:
C(i):=A(i-1)+B(i-1)+P(i)
В виде логической функции это получится так,
,
здесь P(i) перенос в i-ый
разряд
Примечание.
Следует заметить, что выражение для переноса P(i) будет выглядеть совершенно идентично выражению для P(2) и P(i-1), в таком случае можно ограничится синтезом только P(i-1).
Составляется каноническая таблица переходов для поля C(i) (табл. 10)
Таблица 10
|
t |
t+1 |
t |
|||||
|
C(i) |
A(i-1) |
B(i-1) |
P(i) |
C(i) |
P(i-1) |
J |
K |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
01 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
01 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
01 |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
01 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
01 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
01 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
01 |
|
0 |
1 |
1 |
1 |
0 |
1 |
0 |
01 |
|
1 |
0 |
0 |
0 |
1 |
0 |
01 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
01 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
01 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
01 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
01 |
1 |
|
1 |
1 |
0 |
1 |
1 |
0 |
01 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
01 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
01 |
1 |
Составляются функции возбуждения и функция переноса P(i-1) из таблицы 10:
J
|
B(i-1)P(i) C(i)A(i-1) |
00 |
01 |
11 |
10 |
|
00 |
1 |
0 |
1 |
0 |
|
01 |
0 |
1 |
0 |
1 |
|
11 |
* |
* |
* |
* |
|
10 |
* |
* |
* |
* |
K
|
B(i-1)P(i) C(i)A(i-1) |
00 |
01 |
11 |
10 |
|
00 |
* |
* |
* |
* |
|
01 |
* |
* |
* |
* |
|
11 |
0 |
1 |
0 |
1 |
|
10 |
1 |
0 |
1 |
0 |
y>3>:
C(i):=A(i-1)+B(i-1)+P(i),
Аналогично y>2> с заменой в табл. 10 столбца A(i-1) на B(i-1), а B(i-1) на A(i-1), соответственно получается:
y>5>:
C(i):=C(i), необходимо перейти к выражению в виде булевой функции,
Таблица функций возбуждения триггера (табл. 11) будет выглядеть так,
Таблица 11
|
T |
t+1 |
t |
|
|
C(i) |
C(i) |
J |
K |
|
0 |
1 |
1 |
01 |
|
1 |
0 |
01 |
1 |
Из таблицы 11 можно написать выражения для J и K.
J=1
K=1
y>6>:
C(i):=A(i-1)+B(i-1)+P(i), переход к булевой функции,
Составляется каноническая таблица функций возбуждения (табл. 12),
Таблица 12
|
t |
t+1 |
t |
|||||
|
C(i) |
A(i-1) |
B(i-1) |
P(i) |
C(i) |
P(i-1) |
J |
K |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
01 |
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
01 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
01 |
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
01 |
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
01 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
01 |
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
01 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
01 |
|
1 |
0 |
0 |
0 |
0 |
0 |
01 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
01 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
01 |
0 |
|
1 |
0 |
1 |
1 |
0 |
1 |
01 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
01 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
01 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
01 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
01 |
0 |
Составляются функции возбуждения и функция переноса P(i-1) из таблицы 12:
J
|
B(i-1)P(i) C(i)A(i-1) |
00 |
01 |
11 |
10 |
|
00 |
0 |
1 |
0 |
1 |
|
01 |
1 |
0 |
1 |
0 |
|
11 |
* |
* |
* |
* |
|
10 |
* |
* |
* |
* |
K
|
B(i-1)P(i) C(i)A(i-1) |
00 |
01 |
11 |
10 |
|
00 |
* |
* |
* |
* |
|
01 |
* |
* |
* |
* |
|
11 |
1 |
0 |
1 |
0 |
|
10 |
0 |
1 |
0 |
1 |
y>4>:
C(i):=C(i)+P(i)
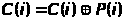
J=P(i)
K=P(i)
P(i-1)=C(i)P(i)
Составляются результирующие функции J, K и P(i-1), по ним на рис. 2.2.6., рис. 2.2.7. изображены логические схемы C(i), P(i-1), а на рис. 2.2.8. и рис. 2.2.9. соответственно даны их условные обозначения.
y>2>
y>3>
y>6>
1
&
C(i)
B(i-1)
1
1
=
=
1
P(i)
A(i-1)
&
y>2>
=
=
1
C(i)
&
y>3>
&
y>6>
y>5>
&
1
y>4>
&
1
1
1
синхр
Рис. 2.2.6.
1
B(i-1)
&
y>2>
1
A(i-1)
1
&
1
1
y>6>
P(i-1)
1
&
1
&
1
&
1
&
y>3>
C(i)
Рис. 2.2.7.
Рис. 2.2.8.
P(i-1)
P(i)
C(i)
А(i-1)
B(i-1)
y>2>
y>3>
y>4>
y>6>
P(i-1)
Рис. 2.2.9.
Поле С(26).
y>2>:
C(26):=A(25)+B(25)
В виде логической функции это получится так,
,
Составляется таблица 13 функций возбуждения элементов памяти, по этой таблице будет так же определяться функция переноса P(25).
Таблица 13
|
t |
t+1 |
t |
||||
|
C(26) |
A(25) |
B(25) |
C(26) |
P(25) |
J |
K |
|
0 |
0 |
0 |
1 |
0 |
1 |
01 |
|
0 |
0 |
1 |
0 |
1 |
0 |
01 |
|
0 |
1 |
0 |
0 |
0 |
0 |
01 |
|
0 |
1 |
1 |
1 |
0 |
1 |
01 |
|
1 |
0 |
0 |
1 |
0 |
01 |
0 |
|
1 |
0 |
1 |
0 |
1 |
01 |
1 |
|
1 |
1 |
0 |
0 |
0 |
01 |
1 |
|
1 |
1 |
1 |
1 |
0 |
01 |
0 |
Составляются функции:
J
|
А(25)В(25) С(26) |
00 |
01 |
11 |
10 |
|
0 |
1 |
1 |
||
|
1 |
1 |
1 |
1 |
1 |
K
|
А(25)В(25) С(26) |
00 |
01 |
11 |
10 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
y>3>:
C(26):= A(25)+ B(25)
В виде логической функции это получится так,
,
Аналогично таблице 13 с заменой столбцов А(25) на В(25) и В(25) на А(25).
y>4>:
С(26):=С(26)+1,
Таблица идентична таблице 11, соответственно функции имеют вид,
J=1, K=1, P(25)=C(26).
y>5>:
С(26):=С(26),
Таблица идентична таблице 11, соответственно функции имеют вид,
J=1, K=1.
y>2>:
C(26):=A(25)+B(25)
В виде логической функции это получится так,
,
Составляется таблица 14 функций возбуждения элементов памяти, по этой таблице будет так же определяться функция переноса P(25).
Таблица 14
|
t |
t+1 |
t |
||||
|
C(26) |
A(25) |
B(25) |
C(26) |
P(25) |
J |
K |
|
0 |
0 |
0 |
0 |
0 |
0 |
01 |
|
0 |
0 |
1 |
1 |
0 |
1 |
01 |
|
0 |
1 |
0 |
1 |
0 |
1 |
01 |
|
0 |
1 |
1 |
0 |
1 |
0 |
01 |
|
1 |
0 |
0 |
0 |
0 |
01 |
1 |
|
1 |
0 |
1 |
1 |
0 |
01 |
0 |
|
1 |
1 |
0 |
1 |
0 |
01 |
0 |
|
1 |
1 |
1 |
0 |
1 |
01 |
1 |
Составляются функции:
J
|
А(25)В(25) С(26) |
00 |
01 |
11 |
10 |
|
0 |
1 |
1 |
||
|
1 |
1 |
1 |
1 |
1 |
K
|
А(25)В(25) С(26) |
00 |
01 |
11 |
10 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
Составляются результирующие функции J, K и P(25), по ним на рис. 2.2.10., рис. 2.2.11. изображены логические схемы C(26), P(25) соответственно, а на рис. 2.2.12. и рис. 2.2.13. соответственно даны их условные обозначения.
y>2>
y>3>
y>6>
C(26)
A(25)
B(25)
y>4>
y>5>
1
1
C(26)
1
1
&
&
1
синхр
Рис. 2.2.10.
y>3>
y>6>
A(25)
y>2>
B(25)
y>4>
1
&
1
&
1
1
P(25)
&
&
C(26)
Рис. 2.2.11.
C(26)
А(25)
B(25)
y>2>
y>3>
y>4>
y>5>
y>6>
С
С(26)
С(26)
Рис. 2.2.12.
P(25)
А(25)
B(25)
C(26)
y>2>
y>3>
y>4>
y>6>
P(25)
Рис. 2.2.13.
3.Разработка функциональной схемы управляющего автомата
3.1 Структурная схема управляющего автомата
В структурном отношении управляющий автомат типа Мура может быть представлен в виде, изображенном на рис. 3.1.1.
T>1>
КС1
КС2
ЭП>1>
V>1>
Y>1>
X>1>
.
.
.
.
.
.
.
.
.
.
.
.
X>L>
V>R>
Y>N>
ЭП>R>
T>R>
Рис. 3.1.1.
Память П автомата
образуют элементарные полные автоматы
Мура – элементы памяти (ЭП), которые
являются JK–триггерами.
Каждому состоянию автомата А>f>
(А>f>
А,
где
- множество состояний автомата)
ставится в соответствие вектор длины
R (R –
количество элементов памяти, образующих
память автомата), компонентами которого
являются состояния ЭП автоиата T>1>,
T>2>,
…,T>R>.
Переход управляющего автомата из
состояния А>d>
в А>f> осуществляется
под действием входного сигнала,
кодируемого вектором длины L;
компонентами этого вектора являются
состояния входов x>1>,
x>2>,
…,x>L>. При этом
на выходе автомата формируется выходной
сигнал, кодируемый вектором длины N;
компонентами этого вектора являются
состояния выходов Y>1>,
Y>2>,
…,Y>L>. Изменения
состояния на переходе
происходит под действием сигналов из
множества
,
формируемых на выходах схемы КС1.
Схема КС2 может быть реализована в виде стандартного блока – дешифратора, выполняющего функции дешифрации состояний автомата: некоторому состоянию А>f> ставится в соответствие сигнал Y>r>=1 на выходе дешифратора.
3.2 Закодированная граф – схема и граф управляющего автомата
Исходной информацией для определения числа входов, выходов и различных состояний, в которых может находиться управляющий автомат, является содержательный граф алгоритма, представленный закодированной граф – схемой алгоритма (ГСА).Каждой операторной вершине содержательного графа можно поставить в соответствие состояние автомата и выходной сигнал Y>n>; условной вершине ставится в соответствие вход x>l> управляющего автомата. ГСА, эквивалентная содержательному графу изображена на рис. 3.2.1.
A>0>
y>1>; Y>1>
A>1>
0
1
1
y>3>; Y>3>
0
y>6>; Y>6>
A>3>
A>6>
y>2>; Y>2>
A>2>
0
1
y>8>; Y>8>
A>8>
y>7>; Y>7>
A>7>
0
1
y>4>; Y>4>
A>4>
1
0
y>5>; Y>5>
A>5>
A>0>
Рис. 3.2.1.
Существуют различные
методы структурного синтеза управляющего
автомата. Одним из таких методов является
графический метод синтеза. Автомат
представляется в виде графа. Количество
вершин графа соответствует количеству
различных отметок A>f>
на ГСА автомата. Производится
кодирование состояний автомата векторами
длины
(где F – мощность множества
А), компонентами которых являются
состояния T>1>,
…,T>R>
ЭП. Полученные в результате
кодирования векторы длины R
записываются в соответствующие вершины
графа.
Связь между T>R> и A>f> показана в таблице 15, DC – дешифратор.
Таблица 15
|
A T |
A>0> |
A>1> |
A>2> |
A>3> |
A>4> |
A>5> |
A>6> |
A>7> |
A>8> |
|
T>1> |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
T>2> |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
|
T>3> |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
T>4> |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
Выход DC |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Путям перехода в ГСА на графе соответствуют дуги, указывающие направления перехода.
Если в ГСА
на пути перехода из вершины с отметкой
A>d> в
вершину с отметкой A>f>
находятся условные вершины,
отмеченные символами x>l>,
то на дугах графа записываются конъюнкции,
ранг которых определяется числом
условных вершин, через которые проходит
путь перехода. При x>l>=0
в конъюнкции появится член
,
в при x>l>=1
его прямое значение.
Граф управляющего автомата представлен на рис. 3.2.2.
1
1
1
1
Рис. 3.2.2.
3.3. Синтез комбинационных схем, реализующих функции возбуждения элементов памяти управляющего автомата
Количество ЭП, составляющих память автомата, определяется по выражению
,
где F – мощность множества А.
Для каждого T>R>
(где
)
по графу составляется каноническая
таблица функций переходов и выходов,
а на основе этих таблиц составляются
функции возбуждения ЭП. Соответственно
для T>1>,
T>2>,
T>3>,
T>4>
это будут таблицы 16, 17, 18, 19.
Таблица 16
|
A |
x>1> |
x>2> |
x>3> |
x>4> |
T>1>(t) |
T>1>(t+1) |
J>1> |
K>1> |
|
A>0> |
--- |
--- |
--- |
--- |
0 |
0 |
0 |
01 |
|
A>1> |
1 |
0 |
--- |
--- |
0 |
0 |
0 |
01 |
|
0 |
1 |
--- |
--- |
0 |
0 |
0 |
01 |
|
|
0 |
0 |
--- |
--- |
0 |
0 |
0 |
01 |
|
|
1 |
1 |
--- |
--- |
0 |
0 |
0 |
01 |
|
|
A>2> |
--- |
--- |
0 |
0 |
0 |
0 |
0 |
01 |
|
--- |
--- |
1 |
--- |
0 |
0 |
0 |
01 |
|
|
--- |
--- |
0 |
1 |
0 |
0 |
0 |
01 |
|
|
A>3> |
--- |
--- |
0 |
0 |
0 |
0 |
0 |
01 |
|
--- |
--- |
1 |
--- |
0 |
0 |
0 |
01 |
|
|
--- |
--- |
0 |
1 |
0 |
0 |
0 |
01 |
|
|
A>4> |
--- |
--- |
--- |
0 |
0 |
0 |
0 |
01 |
|
--- |
--- |
--- |
1 |
0 |
0 |
0 |
01 |
|
|
A>5> |
--- |
--- |
--- |
--- |
0 |
0 |
0 |
01 |
|
A>6> |
--- |
--- |
--- |
1 |
0 |
0 |
0 |
01 |
|
--- |
--- |
--- |
0 |
0 |
1 |
1 |
01 |
|
|
A>7> |
--- |
--- |
--- |
--- |
0 |
0 |
0 |
01 |
|
A>8> |
--- |
--- |
--- |
--- |
1 |
0 |
01 |
0 |
Таблица 17
|
A |
x>1> |
x>2> |
x>3> |
x>4> |
T>2>(t) |
T>2>(t+1) |
J>2> |
K>2> |
|
A>0> |
--- |
--- |
--- |
--- |
0 |
0 |
0 |
01 |
|
A>1> |
1 |
0 |
--- |
--- |
0 |
0 |
0 |
01 |
|
0 |
1 |
--- |
--- |
0 |
0 |
0 |
01 |
|
|
0 |
0 |
--- |
--- |
0 |
1 |
1 |
01 |
|
|
1 |
1 |
--- |
--- |
0 |
1 |
1 |
01 |
|
|
A>2> |
--- |
--- |
0 |
0 |
0 |
0 |
0 |
01 |
|
--- |
--- |
1 |
--- |
0 |
1 |
1 |
01 |
|
|
--- |
--- |
0 |
1 |
0 |
1 |
1 |
01 |
|
|
A>3> |
--- |
--- |
0 |
0 |
0 |
0 |
0 |
01 |
|
--- |
--- |
1 |
--- |
0 |
1 |
1 |
01 |
|
|
--- |
--- |
0 |
1 |
0 |
1 |
1 |
01 |
|
|
A>4> |
--- |
--- |
--- |
0 |
1 |
0 |
01 |
1 |
|
--- |
--- |
--- |
1 |
1 |
1 |
01 |
0 |
|
|
A>5> |
--- |
--- |
--- |
--- |
1 |
0 |
01 |
1 |
|
A>6> |
--- |
--- |
--- |
1 |
1 |
1 |
01 |
0 |
|
--- |
--- |
--- |
0 |
1 |
0 |
01 |
1 |
|
|
A>7> |
--- |
--- |
--- |
--- |
1 |
0 |
01 |
1 |
|
A>8> |
--- |
--- |
--- |
--- |
0 |
0 |
0 |
01 |
Таблица 18
|
A |
x>1> |
x>2> |
x>3> |
x>4> |
T>3>(t) |
T>3>(t+1) |
J>3> |
K>3> |
|
A>0> |
--- |
--- |
--- |
--- |
0 |
0 |
0 |
01 |
|
A>1> |
1 |
0 |
--- |
--- |
0 |
1 |
1 |
01 |
|
0 |
1 |
--- |
--- |
0 |
1 |
1 |
01 |
|
|
0 |
0 |
--- |
--- |
0 |
1 |
1 |
01 |
|
|
1 |
1 |
--- |
--- |
0 |
1 |
1 |
01 |
|
|
A>2> |
--- |
--- |
0 |
0 |
1 |
0 |
01 |
1 |
|
--- |
--- |
1 |
--- |
1 |
0 |
01 |
1 |
|
|
--- |
--- |
0 |
1 |
1 |
0 |
01 |
1 |
|
|
A>3> |
--- |
--- |
0 |
0 |
1 |
0 |
01 |
1 |
|
--- |
--- |
1 |
--- |
1 |
0 |
01 |
1 |
|
|
--- |
--- |
0 |
1 |
1 |
0 |
01 |
1 |
|
|
A>4> |
--- |
--- |
--- |
0 |
0 |
0 |
0 |
01 |
|
--- |
--- |
--- |
1 |
0 |
0 |
0 |
01 |
|
|
A>5> |
--- |
--- |
--- |
--- |
0 |
0 |
0 |
01 |
|
A>6> |
--- |
--- |
--- |
1 |
1 |
1 |
01 |
0 |
|
--- |
--- |
--- |
0 |
1 |
0 |
01 |
1 |
|
|
A>7> |
--- |
--- |
--- |
--- |
1 |
0 |
01 |
1 |
|
A>8> |
--- |
--- |
--- |
--- |
0 |
0 |
0 |
01 |
Таблица 19
|
A |
x>1> |
x>2> |
x>3> |
x>4> |
T>4>(t) |
T>4>(t+1) |
J>4> |
K>4> |
|
A>0> |
--- |
--- |
--- |
--- |
0 |
1 |
1 |
01 |
|
A>1> |
1 |
0 |
--- |
--- |
1 |
0 |
01 |
1 |
|
0 |
1 |
--- |
--- |
1 |
1 |
01 |
0 |
|
|
0 |
0 |
--- |
--- |
1 |
0 |
01 |
1 |
|
|
1 |
1 |
--- |
--- |
1 |
0 |
01 |
1 |
|
|
A>2> |
--- |
--- |
0 |
0 |
0 |
0 |
0 |
01 |
|
--- |
--- |
1 |
--- |
0 |
0 |
0 |
01 |
|
|
--- |
--- |
0 |
1 |
0 |
1 |
1 |
01 |
|
|
A>3> |
--- |
--- |
0 |
0 |
1 |
0 |
01 |
1 |
|
--- |
--- |
1 |
--- |
1 |
0 |
01 |
1 |
|
|
--- |
--- |
0 |
1 |
1 |
1 |
01 |
0 |
|
|
A>4> |
--- |
--- |
--- |
0 |
0 |
0 |
0 |
01 |
|
--- |
--- |
--- |
1 |
0 |
1 |
1 |
01 |
|
|
A>5> |
--- |
--- |
--- |
--- |
1 |
0 |
01 |
1 |
|
A>6> |
--- |
--- |
--- |
1 |
0 |
1 |
1 |
01 |
|
--- |
--- |
--- |
0 |
0 |
0 |
0 |
01 |
|
|
A>7> |
--- |
--- |
--- |
--- |
1 |
0 |
01 |
1 |
|
A>8> |
--- |
--- |
--- |
--- |
0 |
0 |
0 |
01 |
Функциональная схема управляющего автомата приведена на функциональной схеме операционного устройства, где показаны связи между операционным и управляющим автоматами.
4. Функциональная схема операционного устройства
4.1. Организация связи между операционным и управляющим автоматами
Связи между операционным и управляющим автоматами организуются так. Сигналы с выходов управляющего автомата подаются на его же входы, а также на входы операционного автомата. На входы управляющего автомата подаются также сигналы логических условий. Каждая микрооперация выполняется строго при поступлении синхроимпульса и при подаче соответствующего управляющего сигнала, который в свою очередь вырабатывается на основе сигналов логических условий, вычисленных в предыдущий такт работы операционного устройства.
Графически связи между операционным и управляющим автоматами показаны на функциональной схеме операционного устройства, приведенной на масштабно–координатной бумаге.
4.2. Описание работы операционного устройства на заданном отрезке времени
Дано:
А=1.1010010
В=0.0011101
После выполнения
микрооперации y>1>
на входы управляющего автомата приходит
сигнал Y>1>
и сигналы логических условий,
=1
и
=0,
под действием этих сигналов и при
поступлении синхроимпульса из генератора
синхроимпульсов (ГСИ) триггеры
управляющего автомата переходят в
состояния: T>1>=0,
T>2>=0,
T>3>=1,
T>4>=0
(см. общую схему). В свою очередь на
дешифраторе вырабатывается сигнал Y>2>,
при котором в операционном автомате
выполняется микрооперация y>2>.
Которая заключается в следующем. Полю С(1) присваивается значение переноса в этот разряд P(1), который можно вычислить по схеме на рис. 2.2.5., а схема С(1) изображена на рис. 2.2.1. Полю С(2) присваивается значение инверсии переноса в этот разряд P(2) (рис. 2.2.7.), схема С(2) изображена на рис. 2.2.3. На поле С(3:25) происходит присвоение C(i) суммы B(i-1), инверсии A(i-1) и переноса P(i)(схема для С(i) на рис. 2.2.6., а для P(i) на рис. 2.2.7), где i = 3-25. Но перенос P(25) определяется иначе, на основе схемы рис. 2.2.11. На поле С(26) происходит подобная операция (С(26):=А(25)+В(25)) только без учета переноса, так как его не может быть (С(26) – последний разряд), схема дана на рис. 2.2.10. В результате этой микрооперации слово С принимает следующий вид: С=01.1001010
Далее на
входы управляющего автомата подается
сигнал y>2> и
сигналы логических условий
=0
и
=1.
Тогда при поступлении сигнала из ГСИ
и сигнала Y>2>
триггеры управляющего автомата переходят
в состояния: T>1>=0,
T>2>=1,
T>3>=0,
T>4>=1,
что на выходе дешифратора соответствует
сигналу Y>5>, под
действием которого в операционном
автомате выполняется микрооперация
y>5>
(см. общую схему).
При этой микрооперации значения полей С(1) и С(2) не меняются, см. соответственно рис. 2.2.1.и рис. 2.2.3. Разрядам полей С(3:25) и С(26) присваивается значение инверсии этих разрядов, что можно вычислить из схем на соответственно рис. 2.2.6. и рис. 2.2.10. Тогда в данном примере значение слова С будет таким: С=01.0110101
Далее, когда на входы управляющего автомата приходит сигнал Y>5> и сигнал из ГСИ, триггеры управляющего автомата обнуляются, то есть T>1>=0, T>2>=0, T>3>=0, T>4>=0, а на выходе дешифратора вырабатывается сигнал Y>0> (см. общую схему), который означает, что операционное устройство готово к выполнению следующего цикла операции арифметического сложения чисел с фиксированной запятой в обратных двоичных кодах.
Примечание.
В примере использовались восьмиразрядные слова А и В, а также девятиразрядное слово С , то есть полю С(3:25) соответствует поле С(3:8), а полю С(26) поле С(9).
Заключение
В данном курсовом проекте разработано операционное устройство, выполняющее операцию арифметического сложения чисел с фиксированной запятой в обратных двоичных кодах. Также приведена общая схема устройства, состоящая из двух главных частей: операционного автомата и управляющего автомата. В работе предполагалось, что вся информация, необходимая для выполнения операции (операнды А и В), была уже занесена в память устройства.
Литература
Проф. А. А. Эйлер, доц. Р. С. Ефимова, ст. преп. В. В. Жевержеева Методические указания к выполнению курсовой работы по дисциплине "Арифметические и логические основы цифровых автоматов". Ленинград: ЛИИЖТ, 1983
Б. Г. Лысиков Арифметические и логические основы цифровых автоматов Минск: Высшая школа, 1980
Приложение
Прокрутка алгоритма операции приведена в таблице 20.
Таблица 20
|
Пункт алгоритма |
Выполнение микрооперации или вычисление лог. условия |
Условие перехода |
Пункт перехода |
Коментарии |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
А:=0.0011101 В:=0.1010010 |
Безуслов |
2 |
Операнды с одинаковыми знаками (положительные) |
|
2 |
П(1):=0 С(1):=0 |
Безуслов |
3 |
Обнуление |
|
3 |
А(1) |
x>1>=0 |
5 |
Проверка знака слова А |
|
5 |
В(1) |
x>2>=0 |
8 |
Проверка знака слова В |
|
8 |
А:=0.0011101 + В:=0.1010010 С:=00.1101111 |
Безуслов |
9 |
Сложение А и В с занесением в С |
|
9 |
С(2) |
x>4>=0 |
9.2 |
Проверка знака слова С |
|
9.2 |
С(2):=0 |
Безуслов |
10 |
Присвоение С знака А |
|
10 |
Конец |
|||
|
1 |
А:=0.0011101 В:=0.1110011 |
Безуслов |
2 |
Операнды с одинаковыми знаками (положительные) с переполнением |
|
2 |
П(1):=0 С(1):=0 |
Безуслов |
3 |
Обнуление |
|
3 |
А(1) |
x>1>=0 |
5 |
Проверка знака слова А |
|
5 |
В(1) |
x>2>=0 |
8 |
Проверка знака слова В |
|
8 |
А:=0.0011101 + В:=0.1110011 С:=01.0010000 |
Безуслов |
9 |
Сложение А и В с занесением в С |
|
9 |
С(2)=1 |
x>4>=1 |
9.1 |
Проверка знака слова С |
|
9.1 |
П(1):=1 |
Безуслов |
10 |
Регистрация переполнения |
|
10 |
Конец |
|||
|
1 |
А:=1.0011101 В:=1.1010010 |
Безуслов |
2 |
Операнды с одинаковыми знаками (отрицательные) |
|
2 |
П(1):=0 С(1):=0 |
Безуслов |
3 |
Обнуление |
|
3 |
А(1)=1 |
x>1>=1 |
4 |
Проверка знака слова А |
|
4 |
В(1)=1 |
x>2>=1 |
8 |
Проверка знака слова В |
|
8 |
А:=0.0011101 + В:=0.1010010 С:=00.1101111 |
Безуслов |
9 |
Сложение А и В с занесением в С |
|
9 |
С(2) |
x>4>=0 |
9.2 |
Проверка знака слова С |
|
9.2 |
С(2):=1 |
Безуслов |
10 |
Регистрация переполнения |
|
10 |
Конец |
|||
|
1 |
А:=1.0011101 В:=1.1110011 |
Безуслов |
2 |
Операнды с одинаковыми знаками (отрицательные) с переполнением |
|
2 |
П(1):=0 С(1):=0 |
Безуслов |
3 |
Обнуление |
|
3 |
А(1)=1 |
x>1>=1 |
4 |
Проверка знака слова А |
|
4 |
В(1) |
x>2>=0 |
8 |
Проверка знака слова В |
|
8 |
А:=0.0011101 + В:=0.1110011 С:=01.0010000 |
Безуслов |
9 |
Сложение А и В с занесением в С |
|
9 |
С(2)=1 |
x>4>=1 |
9.1 |
Проверка знака слова С |
|
9.1 |
П(1):=1 |
Безуслов |
10 |
Регистрация переполнения |
|
10 |
Конец |
1Продолжение табл. 20
|
1 |
2 |
3 |
4 |
5 |
|
1 |
А:=1.0011101 В:=0.1010010 |
Безуслов |
2 |
Операнды с разными знаками |
|
2 |
П(1):=0 С(1):=0 |
Безуслов |
3 |
Обнуление |
|
3 |
А(1)=1 |
x>1>=1 |
4 |
Проверка знака слова А |
|
4 |
В(1) |
x>2>=0 |
4.1 |
Проверка знака слова В |
|
4.1 |
А:=1.1100010 + В:=0.1010010 С:=10.0110100 |
Безуслов |
6 |
Сложение инверсии А с В и занесением в С |
|
6 |
С(1)=1 |
x>3>=1 |
6.1 |
Проверка переноса из знакового разряда слова С |
|
6.1 |
С(1:26):=С(1:26)+1 С=10,0110101 |
Безуслов |
7 |
Прибавление единицы |
|
7 |
С(2) |
x>4>=0 |
10 |
Проверка знака слова С |
|
10 |
Конец |
|||
|
1 |
А:=0.0011101 В:=1.1010010 |
Безуслов |
2 |
Операнды с разными знаками |
|
2 |
П(1):=0 С(1):=0 |
Безуслов |
3 |
Обнуление |
|
3 |
А(1) |
x>1>=0 |
5 |
Проверка знака слова А |
|
5 |
В(1)=1 |
x>2>=1 |
5.1 |
Проверка знака слова В |
|
5.1 |
А:=0.0011101 + В:=1.0101101 С:=01.1001010 |
Безуслов |
6 |
Сложение инверсии А с В и занесением в С |
|
6 |
С(1) |
x>3>=0 |
7 |
Проверка переноса из знакового разряда слова С |
|
7 |
С(2)=1 |
x>4>=1 |
7.1 |
Проверка знака слова С |
|
7.1 |
С(1:26):=С(1:2).С(3:26) С=01.0110101 |
Безуслов |
10 |
Инвертирование числовых разрядо (образование прямого кода) |
|
10 |
Конец |