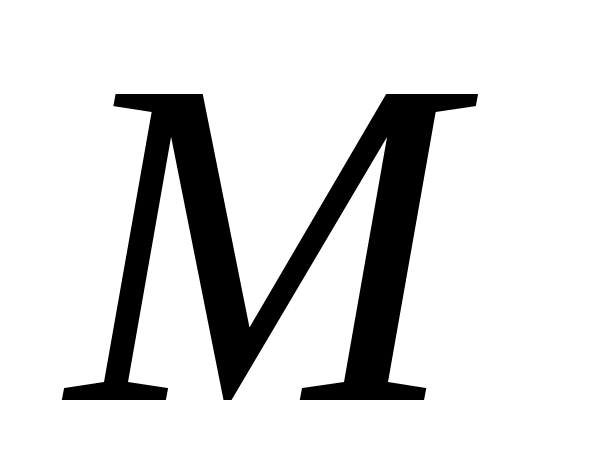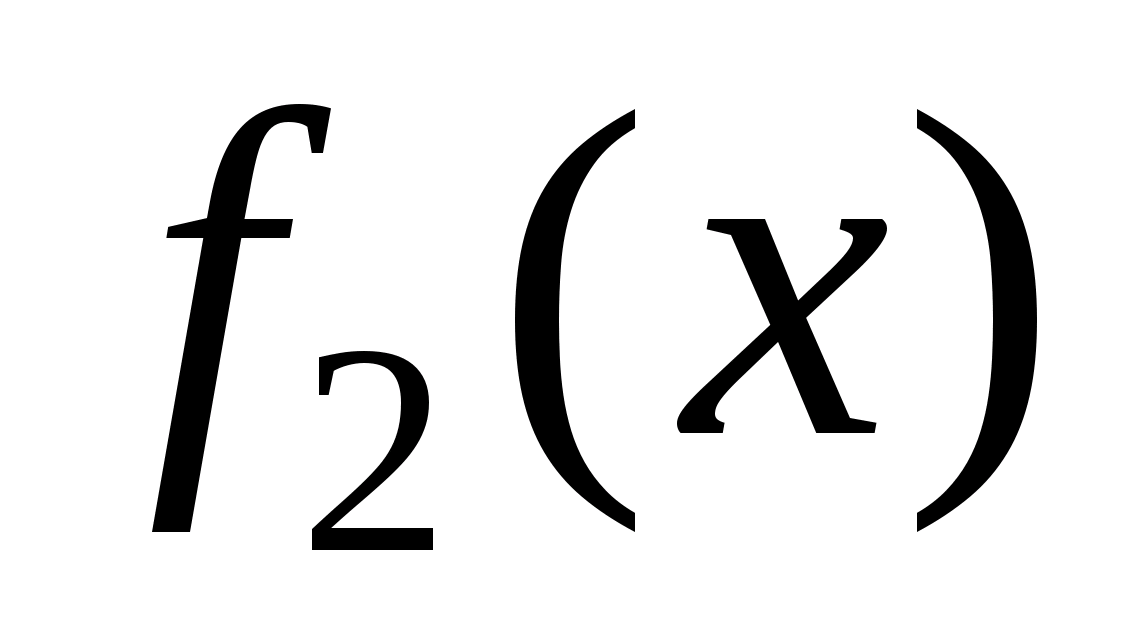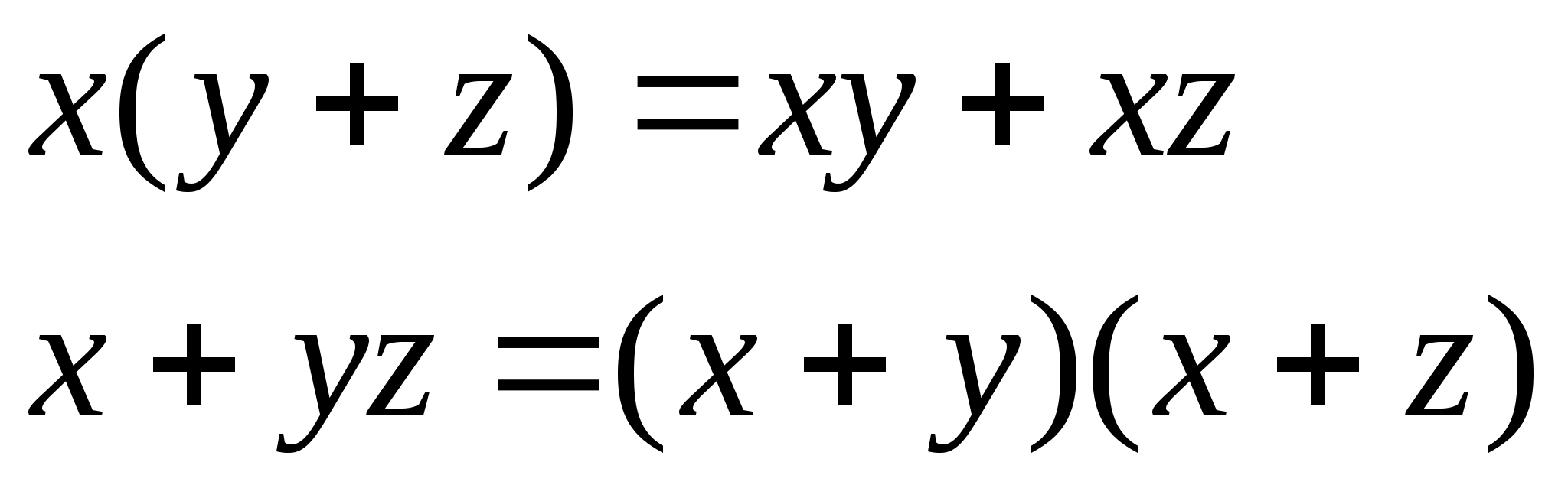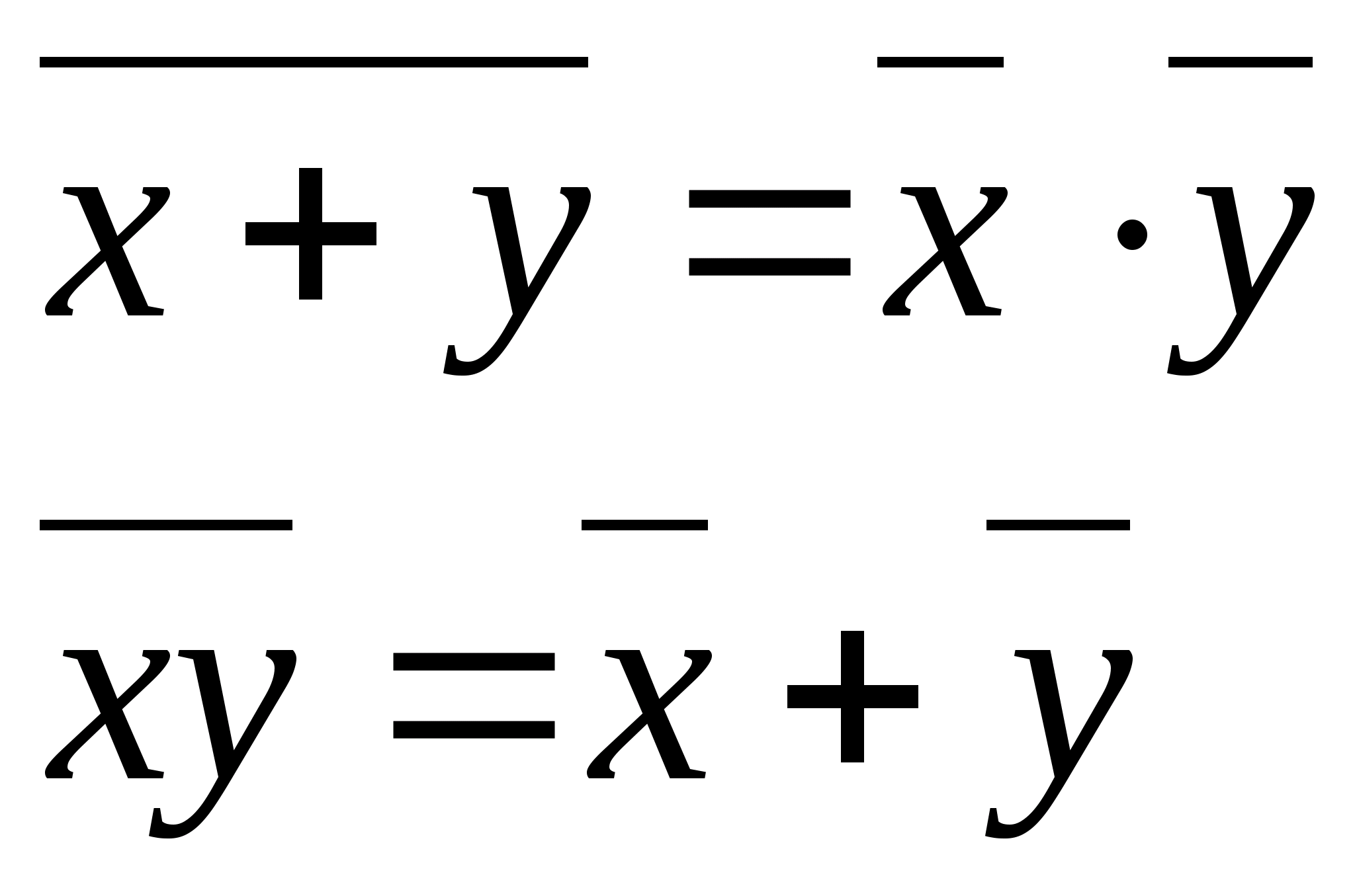Лабораторный практикум
ЛАБОРАТОРНАЯ РАБОТА 1
СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ
1 Цель работы
Настоящая лабораторная работа знакомит студентов с основными логическими функциями и реализующими их элементами широко распространенной I55 серии интегральных микросхем, развивает навык в составлении уравнений, описывающих структуру логических устройств, их минимизации и реализации с учетом имеющегося набора логических элементов.
2 Краткая теория вопроса
2.1 Минимизация булевых функций
Для получения минимальной дизъюнктивной нормальной формы булевой функции воспользуемся методом карт Карно. Карты Карно позволяют достаточно быстро и эффективно минимизировать функции от малого числа (четыре - шесть) аргументов. При этом весьма просто минимизируются неполностью определённые функции. Такой класс функций наиболее часто встречается в проектировании простых узлов ЭВМ, в частности, узлов, синтезируемых на основе конечных автоматов.
Чтобы быстрее нанести булеву функцию, заданную таблично или алгебраически (СДНФ), рекомендуется следующий практический прием.
Основой будем считать карту Карно для четырех аргументов; из двух таких карт формируется карта для пяти аргументов, из четырех таких карт - карта Карно для шести аргументов. Так как аргументы являются переменными двоичного алфавита, то наборы аргументов можно рассматривать как целые двоичные числа.
Взаимное расположение аргументов должно быть чётко фиксированно, например, будем считать, что X>1> - это первый разряд (младший), X>2> - второй разряд, X>3> - третий разряд, X>4> - четвертый разряд и X>5> - старший разряд. Четыре младших разряда определяют номер клетки внутри ос-

а) Карта Карно

б) Карта Карно - “правило четырех Z”
Рисунок 1 - Карты Карно для пяти переменных
новной карты Карно, а пятый разряд задает номер такой карты (0 или 1). Если вместо двоичного кода воспользоваться десятичным эквивалентом, то номера наборов на карте Карно для пяти аргументов можно записать в виде изображённом на рисунке 1.а.
Расположение номеров наборов (клеток) в основной карте Карно легко запоминается по мнемоническому “правилу четырёх Z”. Это правило заключается в следующем: Z большое - это клетки 0,1,2,3; Z узкое - 4,5,6,7; Z широкое - 8,9,10,11; Z малое - 12,13,14,15.
В других картах принцип четырёх Z сохраняется, изменяются только направления и начальные точки (рисунок 1.б).
Если в таблице истинности отсутствуют некоторые строки, что соответствует неиспользованным кодам состояний (избыточное состояние) и запрещенным комбинациям входных сигналов, то в соответствующих клетках карты Карно ставятся прочерки или звёздочки.
На этих наборах (клетках) доопределяются значения функций так, чтобы получилась минимальная ДНФ булевой функции.
2.2 Пороговый элемент
Пороговым элементом называется логический элемент с n двоичными входами X>n >, ... ,X>i >, ... , X>1 >и одним выходом F, причем каждому входу X>i >приписан некоторый “вес” P>i >.
Сигнал на выходе порогового элемента принимает значение “1” только тогда , когда сумма весов входов , на которых сигнал имеет значение “1” (X>i >=1), превосходит некоторый порог l. Таким образом, действие такого однопорогового элемента может быть описано функцией:

Структурой порогового элемента называется упорядоченный набор {P>n >,...,P>i >,...,P>1 >, l). При этом веса и порог могут быть любые действительные значения, однако будем считать их только целочисленными, как положительными, так и отрицательными. Логическая функция, которую реализует пороговый элемент, определяется только его структурой, т.е. значениями весов и порога.
Рассмотрим синтез порогового элемента.
Пример: Построить пороговый элемент в базисе И-НЕ со структурой {-2,1,3,2},т.е. веса P>1>=3,P>2>=1,P>3>=-2 , порог l=2 .
Решение: 1
этап. Построим таблицу функционирования
такого элемента с заданной структурой.
Для этого нам необходимо заполнить
столбец суммы. Значения суммы мы найдем
по формуле
 P>i>X>i>.
P>i>X>i>.
Таблица 1 - Таблица
функционирования
|
X>3> -2 |
X>2> 1 |
X>1> 3 |
|
F l=2 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
3 |
1 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
4 |
1 |
|
1 |
0 |
0 |
-2 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
-1 |
0 |
|
1 |
1 |
1 |
2 |
1 |
2 этап.
Запишем СДНФ полученной функции
F= X>2>X>1>+X>3>X>2>X>1>
X>2>X>1>+X>3>X>2>X>1>
3 этап. После минимизации получим
F= X>1>
X>2>+
X>1>
 =
X>1>(X>2>+
=
X>1>(X>2>+ )
)
4 этап. Приведем полученную функцию в базис И-НЕ

5 этап. Строим схему (рисунок 2).
Частным случаем порогового элемента является мажоритарный элемент с нечетным числом n входов.
2.3 Мажоритарный элемент
Мажоритарным элементом называют логический элемент, работающий по принципу большинства. Принцип большинства

Рисунок 2 - Пороговый элемент
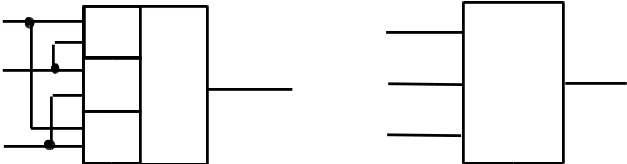
заключается в том, что если большинство входных сигналов равно 1 или 0, то и выходной сигнал будет соответственно равен 1 или 0. Хотя принципиально количество входов мажоритарного элемента может быть равно любому нечётному числу, на практике чаще всего применяются элементы с количеством входов 3 и 5.
Работа мажоритарного элемента на три входа описывается булевой функцией M(X,Y,Z) , определяемой следующей таблицей истинности (таблица 2).
Таблица 2 - Таблица
истинности
|
X |
Y |
Z |
M(X,Y,Z) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
СДНФ данной
функции мажоритарности запишется
M(X,Y,Z)= YZ+X
YZ+X Z+XY
Z+XY .
.
Минимизируя это выражение при помощи карт Карно, получим M(X,Y,Z)=XY+XZ+YZ.
Для этой функции вводится специальное обозначение, которое сокращает запись функции M(X,Y,Z)=XY+XZ+YZ=X#Y#Z.
> >Такая запись означает, что для получения из неё первоначальной минимальной ДНФ надо взять по коньюкции второго ранга по каждой переменной и объединить их знаком дизъюнкции. На рисунке 3 показана схема мажоритарного элемента на три входа и его условное обозначение.
X
&
1
 2
2
Y & M
Z &
а) Мажоритарный элемент б) Условное обозначение
Рисунок 3 - Схема мажоритарного элемента и его условное обозначение
3 Описание лабораторного макета
В лабораторной работе используется ряд комбинационных логических интегральных микросхем 155 серии, логические входы и выходы которых подключены к гнёздам разъёмов, образующих наборное поле на передней панели лабораторного макета. Соединяя гнезда наборного поля проводниками со штеккерами на концах, можно реализовать различные типы комбинационных логических устройств.
Для задания наборов аргументов логических функций используется генератор кодов, основой которого является пятиразрядный счётчик, построенный на Т - триггерах (из элементов 155-ой серии). На прямых выходах счётчика, выведённых на наборное поле передней панели стенда, можно получить 32 различные комбинации или 32 двоичных числа. Через соответствующие гнёзда каждый из пяти разрядов счётчиков может быть установлен в “1” или “0”. Кроме того, подключив вход счётчика (Сч) к выходу генератора одиночных импульсов (“0”-“1”), можно обеспечить последовательный перебор кодовых комбинаций: каждое нажатие кнопки (Кн) увеличивает число, записанное в счётчике, на единицу. Схема и временная диаграмма работы генератора одиночных импульсов, построенного на основе антидребезгового триггера, приведена на рисунке 4.
Для индикации состояний разрядов счётчика, а также логических элементов используются индикаторные лампочки. Горение лампочки означает наличие кода “1” на выходе соответствующего элемента.
Лабораторная установка питается от сети переменного тока напряжением 220 В через блок питания со стабилизированным напряжением 5 В. Включение стенда осуществляется выключателем “Сеть”. Элементы серии 155 оперируют с сигналами двух уровней: низким (от 0 до 0,4В) - логический 0 и высоким (от 2,4В до 5В)- логическая 1.
Состав и количество микросхем, используемых в работе, приведены в приложении А. Обозначения логических микросхем приведены в приложении Б.
Микросхемы
1...7 выполняют простейшие логические
функции И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ. Элементы
8 реализуют функцию ИСКЛЮЧАЮЩЕЕ ИЛИ
(неравнозначность):
 .
Элементы 9,10 выполняют более сложные
логические функции И-ИЛИ-НЕ, например,
работа элемента 9 описывается уравнением
.
Элементы 9,10 выполняют более сложные
логические функции И-ИЛИ-НЕ, например,
работа элемента 9 описывается уравнением
 .
.

Рисунок 4 - Схема генератора одиночных импульсов и временная диаграмма генератора
4 Программа работы
1) Минимизировать следующие логические неполностью определённые функции, заданные в таблице 3, и составить принципиальную схему для реализации.
Таблица 3 - Таблица неполностью определенных функций
|
N |
Принимают значения , равные 1 на наборах |
Принимают значения , равные 0 на наборах |
|
1 |
0, 5, 24, 29 |
3, 7, 8, 13, 16, 21 |
|
2 |
9, 12, 17, 20 |
1, 4, 13, 22 |
|
3 |
15, 19, 23, 31 |
0, 11, 22, 27 |
|
4 |
0, 3, 4, 7 |
5, 10, 22 |
|
5 |
3, 10, 15 |
7, 9, 11 |
|
6 |
13, 14, 21, 22 |
7, 9, 23, 28 |
|
7 |
6, 12, 15, 30 |
3, 14, 19, 31 |
|
8 |
11, 14, 26, 31 |
3, 12, 23, 27 |
|
9 |
2, 15, 18, 31 |
3, 6, 10 |
|
10 |
7, 11, 12, 24 |
1, 14, 22, 29 |
|
11 |
2, 15, 17, 19, 27 |
3, 6, 18, 29, 30 |
|
12 |
3,7, 11, 20, 24, 28 |
1, 14, 22, 29 |
2) Минимизировать следующие полностью определённые логические функции, принимающие значения, равные 1 на указанных наборах, и составить принципиальную схему для их реализации.
|
1. |
0,4,8,10,11,12,14 |
7. |
16,18,20,21,22,26,27,28,29 |
|
2. |
17,20,22,25,26,27,28,30,31 |
8. |
0, 2, 3, 12, 13, 15 |
|
3. |
3,6,7,14,15,19,23,30,31 |
9. |
3, 9, 11, 13, 18, 19, 27 |
|
4. |
1,9,11,17,19,25,27 |
10. |
1, 12, 17, 20, 21, 28, 29 |
|
5. |
0,2,4,8,12,13,16,18,28 |
11. |
3, 6, 7, 14, 27, 30, 31 |
|
6. |
7, 13, 15, 25, 27, 29, 31 |
12. |
0,8,10, 12, 13, 15, 26, 31 |
3) Минимизировать следующие полностью определённые логические функции, принимающие значения, равные 0 на наборах, и составить принципиальную схему для их реализации:
|
1. |
0,1,8,9,17,25,28, 29 |
7. |
1, 9, 25, 27, 28, 29 |
|
2. |
0,8,16,20,24,28 |
8. |
6,14, 15, 22, 23, 30 |
|
3. |
3, 11, 15, 31 |
9. |
9, 13, 15, 27, 29, 31 |
|
4. |
3, 10, 11, 18, 27 |
10. |
7, 14, 15, 22, 30 |
|
5. |
7, 11, 15, 22, 23, 30 |
11. |
9, 11, 23, 30, 31 |
|
6. |
3 , 10 , 11 , 22 , 23 , 30 |
12. |
9 , 11 , 21 , 22 , 23 |
4) Минимизировать схему выбора чисел из 5-разрядного счётчика и составить принципиальную схему для реализации (на выходе схемы выбора должна появиться 1 при подаче на вход любого из выбираемых чисел).
|
1. |
Всех чисел 20 >= M>= 8 . |
|
2. |
Всех чисел M=<7 |
|
3. |
Всех чисел M>8 |
|
4. |
Всех чисел M<7 |
|
5. |
Всех чисел M, кратных 4 ,если M<24 |
|
6. |
Всех чисел 12<M<17 |
|
7. |
Всех чисел 20>M>27 |
|
8. |
Всех чисел 12=<M<24 |
|
9. |
Всех нечётных чисел 11<M<26 |
|
10. |
Всех чётных чисел 11<M=<26 |
|
11. |
Всех чисел 7=<M=<15 и 20=<M=<24 |
5) Минимизировать системы функций, описывающих преобразователи одного кода в другой. Коды заданы ниже.
|
1. |
I-II |
7. |
V-I |
13. |
V-III |
|
2. |
I-III |
8. |
VI-I |
14. |
VI-III |
|
3. |
I-IV |
9. |
IV-II |
15. |
VI-IV |
|
4. |
I-V |
10. |
V-II |
16. |
V -IV |
|
5. |
I-VI |
11. |
VI-II |
17. |
VI-V |
|
6. |
IV-I |
12. |
IV-III |
18. |
III-I |
6) Построить
схему порогового элемента на К входов
(выходной сигнал равен 1, если суммарное
число единиц на входах не меньше, чем
значение порога P) при разных весовых
коэффицентах
 входов, указанных в таблицах 4 и 5.
входов, указанных в таблицах 4 и 5.
Таблица 4 - Таблица Таблица 5 - Таблица
|
N |
K |
P |
|
|
1 |
3 |
2 |
1 |
|
2 |
4 |
2 |
1 |
|
3 |
4 |
3 |
1 |
|
4 |
5 |
3 |
1 |
|
5 |
5 |
4 |
1 |
|
6 |
5 |
2 |
1 |
|
7 |
5 |
4 |
2 |
|
N |
K |
P |
|
|
8 |
5 |
4 |
2,1,2,1,2 |
|
9 |
5 |
3 |
1,2,1,2,1 |
|
10 |
4 |
2 |
1,1,1,2 |
|
11 |
4 |
3 |
2,1,1,2 |
|
12 |
5 |
3 |
1,1,1,1,3 |
|
13 |
4 |
3 |
1,1,1,2 |
|
14 |
5 |
5 |
1,2,3,4,5 |
7) Построить схему сравнения двухразрядных кодов M и P, принимающих значение 1 в следующих случаях:
1) M=P; 2) M<P;
3) M>P; 4) M=<P; 5) M>=P; 6) M
 P.
P.
8) Построить мажоритарный элемент на 5 входов
В процессе выполнения работы после сборки схемы требуется проверить правильность функционирования последней и устранить допущенные ошибки. Ошибки могут быть сделаны или во время формального синтеза схемы или во время сборки узла. Методика отыскания и устранения ошибок проектирования и синтеза узла заключается в следующем.
Детальному рассмотрению подвергают исходное состояние и комбинацию входных сигналов, при действии на которых выполняется неверный переход, т.е. не соответствующий заданной таблице переходов или выходов устройства. В первую очередь делают подстановку исследуемого набора аргументов в функции возбуждения и выхода и убеждаются, что формально устройство переводится в нужное состояние и формируется заданное значение функции выхода. Если эти условия не выполняются, то ошибка произошла во время формального синтеза и необходимо тщательно перепроверить его этапы.
В противном случае ошибка допущена при сборке узла, тогда поиск ее ведется следующим образом. Для данного исходного состояния устройства и комбинации входных сигналов с помощью индикатора проверяются значения всех функций возбуждения и функций выхода. Если значения каких-либо функций не соответствуют таблице истинности, то ошибки следует искать в комбинационных схемах этих функций.
Последовательно продвигаясь от выхода комбинационной схемы ко входам, с помощью индикатора проверяют значения сигналов на выходах и входах промежуточных логических элементов. Эти значения сверяют с ожидаемыми, которые получают подстановкой данного набора аргументов в исследуемую функцию возбуждения или выхода. Несоответствие значений свидетельствует о неисправности логического элемента или о неправильном соединении элементов. После устранения неисправности повторяют полную проверку функционирования заданного устройства по таблице переходов и выходов.
5 Содержание отчёта
В результате выполнения рабочего задания должны быть подготовлены таблицы логических функций, заполненные карты Карно, принципиальные схемы синтезируемых устройств. По указанию преподавателя для ряда синтезированных схем составляются соответствующие дуальные схемы. На занятии производится сборка схем и проверка правильности их функционирования.
Защита работы производится при представлении отчёта, который должен содержать: индивидуальные задания; минимизацию функции выбранным методом; аналитические уравнения минимизированных функций; уравнения, соответствующие выбранному схемотехническому решению; принципиальные схемы.
6 Контрольные вопросы
6.1 Чем отличаются полностью определённые логические функции от неполных? Как производится их минимизация?
6.2 Как проводится минимизация логических уравнений с шестью переменными?
6.3 Нарисуйте структуру порогового элемента.
6.4 Чем отличается мажоритарный элемент от порогового?
6.5 Дайте понятия основной и дуальной схемы.
Список литературы
1. Шило В.Л. Популярные цифровые микросхемы. - Челябинск: Металлургия, 1989.
2. Алексенко А.Г., Шагурин И.И. Микросхемотехника. - М.: Радио и связь, 1990.
3. Зельдин Е.А. Цифровые интегральные микросхемы в информационно-измерительной аппаратуре. -Л.: Энергоатомиздат,1986.
ЛАБОРАТОРНАЯ РАБОТА 2
ИССЛЕДОВАНИЕ БИСТАБИЛЬНЫХ ЯЧЕЕК
1 Цель работы
Целью настоящей работы является научить студентов самостоятельно проводить анализ различных типов бистабильных ячеек; выявлять в этих схемах опасные состязания (критические гонки); на основании теоретического анализа составлять функции переходов указанных ячеек; при определенных условиях уметь устранять опасные состязания.
2 Краткая теория вопроса
Схемы, составленные из логических элементов и имеющие петли, называются логическими схемами с обратными связями. Петлей называется такая цепь, у которой выход последнего элемента схемы соединен хотя бы с одним входом первого элемента.
Отметим, что общим свойством комбинационных схем является отсутствие петель.
Функционирование схем с обратными связями не может быть полностью описано системой переключательных функций. Особенностью логических схем с обратными связями является зависимость состояния выходов схемы не только от значений входных переменных в данном такте, но и от сигналов, действовавших в предыдущие моменты времени. Поэтому такая схема может рассматриваться как цифровой автомат.
Считается, что схема с обратной связью находится в устойчивом состоянии, если состояние ее выходов может сохраняться неограниченно долго.
Неустойчивым состоянием схемы будет такое, которое существует лишь короткое время, соизмеримое с длительностью переходных процессов в схеме.
Наличие в схеме двух и более устойчивых состояний указывает на то, что схема может быть использована для запоминания некоторых сигналов, поступающих на схему по внешним цепям.
В качестве элементарного примера анализа схемы с обратными связями рассмотрим схему, построенную на логических элементах ИЛИ-НЕ, которая представлена на рисунке 1.
Нетрудно убедиться, что выходная переменная z удовлетворяет следующему логическому уравнению
 .
(1)
.
(1)
Для решения этого уравнения составим таблицу соответствия входных и выходных переменных (таблица 1). Под решением уравнения будем понимать набор констант x, y, z, подстановка которых в исследуемое уравнение (1) превращает его в тождество.
Из таблицы 1 следует, что решением уравнения (1) будут следующие наборы констант: 0 0 1; 1 0 0; 1 0 1; 1 1 0. Таким образом, входным наборам xy=00 и xy=11 всегда будет соответствовать выходное значение z=1 и z=0 соответственно.
Для этих наборов существует единственное решение, которое не зависит от состояния выхода z.
Если же на вход схемы подать сигналы xy=10, то выход z может принимать как значение нуля, так и единицы, т.е. сигнал на выходе будет зависеть от состояния схемы, которое в свою очередь зависит от сигналов, действовавших в предыдущие моменты времени.
Для этих наборов существует единственное решение, которое не зависит от состояния выхода z.
Если же на вход схемы подать сигналы xy=10, то выход z может принимать как значение нуля, так и единицы, т.е. сигнал на выходе будет зависеть от состояния схемы, которое в свою очередь зависит от сигналов, действовавших в предыдущие моменты времени.

Рисунок 1 - Логическая схема на ИЛИ-НЕ
Таблица 1 - Таблица соот-
ветствия
|
x |
y |
z |
|
|
0 0 |
0 0 |
0 1 |
1 1 |
|
0 0 |
1 1 |
0 1 |
1 0 |
|
1 1 |
0 0 |
0 1 |
0 1 |
|
1 1 |
1 1 |
0 1 |
0 0 |
элементов D>1 >и D>2 >одновременно установится сигнал 0. Через время 2t на выходе элемента D>3 >установится сигнал 1, а через время 3t на выходе z установится сигнал 0 и т.д., т.е. на выходе схемы будут происходить изменения сигнала с 0 в 1 и с 1 в 0. Учтем, что на входе комбинация сигналов (xy=01) при этом не изменяется.
Таким образом, в этой схеме будут происходить колебания с периодом 6t.
При малой величине t (большой частоте) колебания могут сорваться из-за того, что передача сигнала при такой частоте будет происходить без восстановления уровня (без усиления). В этом случае на выходе установится некоторая промежуточная нестандартная амплитуда сигнала. Аналогичная ситуация будет иметь место, если правую часть уравнения (1) реализовать на элементах (диодах) типа ИЛИ и И, не обладающих свойством восстановления уровня сигнала.
Следовательно, логическая схема с обратной связью в зависимости от комбинации входных сигналов может быть конечным автоматом или вообще будет неправильно функционировать (выдавать нестандартный сигнал, либо генерировать колебания).
Однако схемы с обратной связью, имеющие много входов и выходов, анализировать подобным образом трудно, т.к. таблицы согласования в форме таблицы истинности становятся очень громоздкими. В таком случае используют другую форму таблицы соответствия, а именно, карту Карно. Строго определенный порядок перечисления переменных облегчает отображение на картах Карно кодировки внутренних состояний и их устойчивости, что обуславливает удобство использования этого вида карт для анализа и синтеза последовательностных схем.
Рассмотрим конкретный пример анализа логической ячейки типа И-НЕ, охваченной обратными связями (рисунок 2). Эта схема (и подобные другие) получили название бистабильных ячеек (БЯ).
Анализ БЯ будем проводить поэтапно по следующей методике:
2.1 Запишем логические уравнения выходов схемы
 .
(2)
.
(2)

Рисунок 2 - Бистабильная ячейка типа И-НЕ
2.2 Составим карту Карно, при помощи которой будем решать эту систему.
Столбцы этой карты обозначим всевозможными комбинациями независимых (входных) переменных x>1>> >и x>2>, а строки - комбинациями зависимых (выходных) переменных y>1>> >и y>2>> >(таблица 2). В клетки этой карты запишем истинные значения функций y>1>> >и y>2>, определенные в соответствии с приведенной системой уравнений (2). Таким образом, в клетках будет записано двузначное двоичное число, при этом первый разряд будет соответствовать значению y>1>, а второй разряд этого числа - значению y>2>.


Очевидно, что состояние схемы является устойчивым, если значения функций y>1>> >и y>2>> > совпадают с обозначением соответствующей строки таблицы.
Например, при пересечении столбца 01 и строки 10 находится устойчивое состояние 10, а на пересечении того же столбца и строки 11 - неустойчивое состояние 10.
Иногда таблицу 2 представляют в другой форме и называют таблицей переходов (таблица 3). Здесь кружками обозначены устойчивые состояния, точками - неустойчивые, а стрелки указывают направления переходов. Рассмотрим подробнее, как осуществляется переход схемы из неустойчивого состояния в устойчивое. При этом возможны два случая:
1) Код неустойчивого состояния в карте Карно совпадает с кодом устойчивого состояния.
2) Код неустойчивого состояния не совпадает с кодом устойчивого.
В первом случае при фиксированных значениях независимых переменных х>1>> >и х>2>> >выходные сигналы y>1>> >и y>2>, соответствующие неустойчивому состоянию, подаются на входы y>1>> >и y>2>> > схемы, тем самым обуславливая переход к строке карты Карно, соответствующей устойчивому состоянию.
Например, пересечение столбца 10 и строки 11 соответствует неустойчивому состоянию 01. Однако при подаче на y>1>> >и y>2>> >схемы комбинации 01 и при прежних значениях х>1>> >и х>2>> > схема переходит в уже устойчивое состояние 01.
Во втором случае при фиксированных х>1>> >и х>2>> > выходные сигналы y>1>> >и y>2>> > обуславливают переход к новой строке карты Карно, где эти же значения y>1>> >и y>2>> > являются входными и так далее, пока не возникнет ситуация, предусмотренная первым случаем.
Отметим, что в реальных схемах вследствие конечности и разброса времени переключения элементов при переходе схемы из неустойчивого состояния в устойчивое могут появляться промежуточные наборы значений зависимых переменных. Промежуточные значения - это те состояния, которые могут иметься между исходными неустойчивыми и конечным устойчивым.
Например, для столбца 01 и строки 00 мы имеем неустойчивое состояние 11. После поступления этих сигналов (y>1>y>2>=11) на вход схемы возникнет неустойчивое состояние 10 (строка 11), код которого совпадает с кодом устойчивого состояния 10 (строка 10), т.е. мы пришли к первому случаю.
Рассмотренные случаи неустойчивых состояний в конечном итоге приводят к устойчивому состоянию схемы, это столбцы х>1>х>2>, соответствующие 00, 01, 10.
Таким образом, наличие нескольких путей для переходов, кончающихся одним и тем же устойчивым состоянием, является так называемыми некритическими (неопасными) состязаниями (гонками).
Иной случай
можно наблюдать в столбце 11. В этом
столбце имеют место два устойчивых
состояния y>1>>
>и
y>2>>
>=01
и y>1>>
>и
y>2>>
>=10.
Поэтому из неустойчивых состояний y>1>>
>и
y>2>>
>=00
и y>1>>
>и
y>2>>
>=11
может начаться циклический процесс
перехода из состояния 11 (строка 00) в
состояние 00 (строка 11) и наоборот, т.е.
могут возникнуть колебания:
 .
.
Это явление свидетельствует о наличии в схеме критических (опасных) состязаний (гонок). Естественно, что такое явление недопустимо в схемах, предназначенных для запоминания информации. Кроме того, если время задержки элементов несколько отличается, то в этом столбце из каждого неустойчивого состояния возможен переход в любое из устойчивых состояний, т.е. состояние схемы не будет зависеть от выходных сигналов . Таким образом, таблица переходов позволяет наглядно проверить логическое функционирование проектируемой структуры, в частности, установить наличие состязаний.
Для того, чтобы рассматриваемую схему можно было использовать для запоминания информации, необходимо запретить одновременное обращение в нуль х>1> и х>2> , т.е. исключить столбец карты Карно с х>1>х>2> =00, т.к. устойчивым состоянием в этом столбце является состояние у>1>у>2> =11, при котором нарушается бистабильность схемы. Состояние у>1>у>2>=11 неудобно тем, что после изменения независимых входных переменных х>1>> >и х>2>> >от значений х>1>х>2>> >=00 к значениям х>1>х>2>=11 схема может перейти в состояние 01 или 10, иначе говоря, переход будет неопределенным.
Исключить первый столбец карты Карно можно, наложив ограничения на допустимые комбинации входных сигналов, а именно
х>1>+х>2> =1. (3)
Критические состязания исключаются, если разрешенными комбинациями входных сигналов, производящих переключение схемы из одного состояния в другое, будут комбинации 01 и 10. В этом случае при подаче сигналов х>1>х>2>=11 схема будет сохранять то устойчивое состояние, которое установилось предыдущей разрешенной комбинацией входных сигналов.
Так, например, если до х>1>х>2>=11 был сигнал х>1>х>2>=01, у>1>у>2> будет 10 (устойчивое состояние). После поступления сигнала х>1>х>2>=11 схема останется в том же устойчивом состоянии у>1>у>2>=10. Если до х>1>х>2>=11 был сигнал х>1>х>2>=10, то схема будет в состоянии 01, после прихода сигнала х>1>х>2>=11 схема останется в этом же устойчивом состоянии.
Таким образом, при подаче сигналов х>1>х>2>=11 состояния у>1>у>2>=11 и у>1>у>2>=00 будут отсутствовать и критические состояния исчезнут.
Следовательно, в этом случае мы получили логическую схему (ячейку) с двумя устойчивыми состояниями 01 и 10, т.е. бистабильную.
2.3 До сих пор процессы в схеме рассматривались при фиксированных значениях х>1> и х>2> . Рассмотрим теперь поведение схемы при изменении входных независимых переменных. Для удобства записи обозначим состояние схемы, соответствующее у>1>у>2>=01 в момент времени t через Qt=0; состояние у>1>у>2>=10 - через Qt=1, а состояние схемы в момент времени t+1 - через Qt+1. Тогда зависимость
Qt+1=f(х>1>,х>2>,Qt) (4)
можно представить в виде следующей таблицы функционирования бистабильной ячейки (таблица 4).
Таблица 4 - Таблица функ-
ционирования
|
х>1> |
х>2> |
Qt |
Qt+1 |
|
0 0 |
0 0 |
0 1 |
* * |
|
0 0 |
1 1 |
0 1 |
1 1 |
|
1 1 |
0 0 |
0 1 |
0 0 |
|
1 1 |
1 1 |
0 1 |
0 1 |








2.4. Для установления закона функционирования схемы по отношению к переменным х>1>, х>2> и Qt, составим уравнение и, доопределив функцию Qt+1, найдем ее минимальную форму:

 (5)
(5)
Эту функцию называют функцией переходов бистабильной ячейки на логических элементах И-НЕ.
 (6)
(6)
Qt+1
=
 +
x>2>Qt
+
x>2>Qt
1 = x>1> + x>2>> > (7)
Совместная система называется характеристическими уравнениями бистабильной ячейки.
Примечание - чтобы получить таблицу 4 из таблицы 2, нужно последнюю представить в виде:
Qt+1 x>1>x>2>
y>1>y>2> 00 01 11 10
-------------
01
 0 * 1 0 0
0 * 1 0 0
-------------
10
 1 * 1 1 0
1 * 1 1 0
При этом учитываются: ограничение х>1>+х>2>=1, обозначения 01<=>0; 10<=>1, и что неустойчивые состояния в столбцах 01 и 10 переходят в устойчивые: 1 и 0 соответственно. Таким образом, карта Карно с 16 клетками превращается в карту с 8 клетками.
Мы провели полный анализ бистабильной ячейки типа И-НЕ и показали, что при определенных ограничениях такая ячейка может фиксировать 0 и 1 неопределенно долгое время, т.е. является запоминающим элементом.
3 Описание лабораторного макета
На лицевой панели лабораторной установки изображены восемь схем бистабильных ячеек разных типов. С помощью соединительных проводов выходы схемы подключаются к световому индикатору, при помощи которого визуально можно наблюдать процессы переходов в ячейках.
С помощью тумблеров на входы схем можно подавать через соединительные провода высокие и низкие уровни напряжений.
4 Программа работы
Провести полный анализ заданных бистабильных ячеек согласно полученному варианту.
Определить некритические и критические гонки, дать рекомендации по применению рассматриваемых бистабильных ячеек качестве запоминающего элемента. Составить таблицу функционирования ячейки. Получить характеристическое уравнение ячейки. Снять осциллограммы колебательных процессов, возникающих в бистабильной ячейке, зафиксировать частоту , при которой происходит срыв колебаний, определить период колебаний.
5 Содержание отчета
Отчет должен содержать:
а) поэтапный анализ БЯ;
б) таблицы переходов и функционирования;
в) характеристическое уравнение;
г) осциллограммы колебаний;
д) период колебаний, полученный теоретически и практически;
е) временные диаграммы работы ячеек.
6 Контрольные вопросы
6.1 Почему логические элементы с обратными связями не могут быть полностью описаны простой системой булевых функций?
6.2 Как определяются коды устойчивых и неустойчивых состояний логической схемы с обратными связями?
6.3 Что собой представляет таблица переходов логической схемы с обратными связями?
6.4 Каким образом можно устранить критические состязания?
6.5 Чем отличаются характеристические уравнения от логических уравнений комбинационных схем?
Список литературы
1. Шило В.Л. Популярные цифровые микросхемы. - Челябинск: Металлургия, 1989.
2. Алексенко А.Г., Шагурин И.И. Микросхемотехника. -М.: Радио и связь, 1990.
3. Скаржепа В.А., Луценко А.Н. Электроника и микросхемотехника.- Киев.: Выща школа, 1989.
4. Применение интегральных микросхем в электронной вычислительной технике / Под ред. Б.В. Тарабрина.- М.: Радио и связь, 1987.
5.Зельдин Е.А. Цифровые интегральные микросхемы в информационно-измерительной аппаратуре.- Л.:Энергоатомиздат, 1986.
ЛАБОРАТОРНАЯ РАБОТА 3
СИНТЕЗ ЭЛЕМЕНТАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТНЫХ АВТОМАТОВ
1 Цель работы
Целью работы является изучение методики синтеза элементарных последовательностных автоматов на основе бистабильных ячеек по заданной минимизированной таблице его функционирования и построение на этой основе принципиальной схемы с установочными входами.
Студент должен уметь написать характеристическое уравнение любого заданного автомата, построить его временную диаграмму работы, а также обязательно таблицу переходов, без которой невозможно строить сложные узлы на основе заданного автомата.
2 Теория вопроса
2.1 Общие сведения
Элементарными последовательностными автоматами (конечными автоматами, триггерами) принято считать автоматы, которые характеризуются следующими свойствами:
1) Число входных переменных - не более трех. В это число не входят тактовый (синхронизирующий) вход, на который подаются синхроимпульсы, фиксирующие смену тактов работы триггера, установочные входы, входы выборки кристалла и т.п.
2) Число внутренних состояний равно двум, чему соответствует одна внутренняя переменная, которую принято обозначать символом Q.
3) Число
выходных переменных - одна. Обозначается
буквой “у”, причем значение “у”
совпадает со значением Q (т.е. функция
выхода y(t)= Q(t)). Обычно имеется возможность
наряду со значением Q получать инверсную
переменную
 .
.
4) Число реакций автомата - пять (это же число состояний выхода). Перечислим эти реакции:
а) переходить
в состояние
 ;
;
б) переходить
в состояние
 ;
;
в) сохранить
предыдущее состояние неизменным
 ;
;
г) изменить
свое состояние на противоположное
 ;
;
д)
неопределенное состояние, обозначаемое
звездочкой (*) или буквой Х, что запрещает
подачу входного сигнала
 .
.
Функции переходов, называемые характеристическими уравнениями, являются полными:
 ,
,
Разновидности триггеров отличаются не только числом входов (n), но и при одинаковом n - функциями переходов.
Число различных
типов триггерных устройств (N), которые
можно формально создать при n-входной
системе, определяется как
 .
.
Так, например, для устройств с двумя входами, для которых возможны четыре комбинации сигналов на входе (00, 01, 10, 11), и пятью состояниями выхода, существует 625 вариантов триггерных схем.
Однако в реальном проектировании практическое применение имеет небольшое число триггеров, к которым относятся триггеры типов D, RS, T, RST, JK и некоторые другие.
В основу классификации потенциальных триггеров положены два основных признака:
1) функциональный признак;
2) способ записи информации.
Функциональная классификация является наиболее общей и представляет собой классификацию триггеров по виду логического уравнения, характеризующего состояние входов и выходов триггера в момент времени до его срабатывания (t) и после его срабатывания (t+1).
Классификация по способу записи информации характеризует временную диаграмму работы триггера, т.е. определяет ход процесса записи информации в триггер. По этой классификации автоматы подразделяются на две группы:
1) асинхронные;
2) тактируемые (синхронные).
Отличительной особенностью асинхронных автоматов является то, что запись информации в них осуществляется непосредственно с поступлением информационного сигнала на его вход.
Запись информационного сигнала в синхронные автоматы, имеющие информационные и тактовые входы, осуществляется только при подаче разрешающего, тактирующего импульса.
2.2 Синтез автомата
Синтез триггерных устройств заключается в общем виде в выполнении следующих этапов:
1) По заданной таблице функционирования проектируемого автомата составляется его логическое уравнение
2) Выбирается (если не задается) тип бистабильной ячейки и записывается ее полное характеристическое уравнение.
3) Из сопоставления таблицы функционирования проектируемого автомата с характеристическим уравнением бистабильной ячейки получают выражения функций возбуждения бистабильной ячейки и минимизируют их.
4) Уравнения функций возбуждения переводят в тот же базис, в котором записано уравнение бистабильной ячейки; это будет базис ИЛИ-НЕ или И-НЕ.
5) На основании полученных уравнений строят входную комбинационную логику (схему) и соединяют ее с бистабильной ячейкой. При этом предусматривают два установочных входа (S и R), т.е. входы, не зависящие ни от наличия (отсутствия) информационных сигналов, ни от входа синхронизации. Наличие сигналов на установочных входах переводит автомат в состояние 1 или 0.
6) Для полученной схемы автомата составляют таблицу переходов. Это необходимо для того, чтобы можно было легко строить на основе этого автомата более сложные схемы, такие как регистры, счетчики и т.п.
Наиболее трудоемким процессом считается выполнение пункта 3; выполнение остальных пунктов не представляет никаких сложностей.
Методика синтеза не зависит от числа информационных входов автомата.
Для примера проведем анализ синхронного автомата с одним информационным входом, таблица функционирования которого задана в следующем виде и представлена в таблице 1. Отметим, что эта таблица соответствует работе D-триггера (D-информационный вход).
Таблица 1 - Таблица функционирования
-
Ct
Dt
Qt
Qt+1
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
Эту таблицу можно минимизировать до четырех строк и записать так, как показано в таблице 2.
Таблица 2 - Минимизированная таблица
-
Ct
Dt
Qt+1
0
0
Qt
0
1
Qt
1
0
0
1
1
1
Таблицу 2 можно прочитать следующим образом: “При отсутствии сигнала на синхровходе независимо от сигнала на информационном входе состояние автомата не изменяется, при наличии сигнала на синхровходе - автомат принимает то же самое значение, что и сигнал на информационном входе”.
Синтез автомата будем проводить поэтапно согласно указанной выше методике.
1) Составляем по таблице функционирования логическое уравнение синтезируемого автомата

Минимизируя
полученное уравнение, будем иметь
 (1)
(1)
2) Выбираем бистабильную ячейку типа И-НЕ. Ее полное характеристическое уравнение имеет вид
 (2)
(2)
Теперь задача состоит в том, чтобы “заставить” бистабильную ячейку “работать” по заданной таблице функционирования синтезируемого автомата.
Для этого
нам надо разработать входную логику к
этой схеме ячейки, т.е. найти функции
возбуждения по входам
 и
и
 .
.
3) Составим
кодированную таблицу синтезируемого
автомата, в которую включим также столбцы
для определения функций возбуждения
 и
и
 бистабильной ячейки (таблица 3).
бистабильной ячейки (таблица 3).
Таблица 3 - Кодированная таблица
-
N
Ct
Dt
Qt
Qt+1
x>1>
x>2>
0
0
0
0
0
1
*
1
0
0
1
1
*
1
2
0
1
0
0
1
*
3
0
1
1
1
*
1
4
1
0
0
0
1
*
5
1
0
1
0
1
0
6
1
1
0
1
0
1
7
1
1
1
1
*
1
Подставим
из нулевой, второй и четвертой строк
табл. 3 значения
 и
и
 в систему характеристического уравнения
(1) бистабильной ячейки:
в систему характеристического уравнения
(1) бистабильной ячейки:
 (3)
(3)
и разрешим
их относительно
 и
и
 .
.
Для решения
этих уравнений составим таблицу
аргументов для всех наборов
 и
и
 и значений правых частей уравнений.
и значений правых частей уравнений.
Таблица 4 - Таблица аргументов

Значения
правых частей уравнения (3) получаются
при подстановке наборов значений
 и
и
 из таблицы 4 в эти уравнения.
из таблицы 4 в эти уравнения.
Очевидно,
решением уравнения (3) будут такие
значения
 и
и
 ,
при которых правые части тождественно
равны левой части для обоих уравнений
одновременно. Этому условию удовлетворяют
наборы переменных
,
при которых правые части тождественно
равны левой части для обоих уравнений
одновременно. Этому условию удовлетворяют
наборы переменных

 =10
и
=10
и

 =11.
Из таблицы 4 видно, что эта система (3)
имеет два решения
=11.
Из таблицы 4 видно, что эта система (3)
имеет два решения
 =11,
а
=11,
а
 может быть равным как нулю (третий
набор), так и единице (четвертый набор).
Поэтому значение
может быть равным как нулю (третий
набор), так и единице (четвертый набор).
Поэтому значение
 является неопределенным и может
выбираться произвольно, исходя из
соображений максимальной простоты
реализации.
является неопределенным и может
выбираться произвольно, исходя из
соображений максимальной простоты
реализации.
Таким образом,
для рассматриваемых строк таблицы 3
будем иметь
 =1,
=1,
 - не определено (*). Заносим эти значения
в таблицу 3 по строкам 0, 2, 4.
- не определено (*). Заносим эти значения
в таблицу 3 по строкам 0, 2, 4.
Для того,
чтобы сократить процесс определения
функций возбуждения
 и
и
 ,
составим сводную таблицу (таблица 5)
для нахождения
,
составим сводную таблицу (таблица 5)
для нахождения
 и
и
 при различных значениях
при различных значениях
 и
и
 .
.
Таблица 5 - Сводная таблица

Характеристическое уравнение для первой (третьей, седьмой), пятой и шестой строк таблицы 3 будет соответственно иметь вид:
 (4)
(4)
 (5)
(5)
 (6)
(6)
Из таблицы 5 получаем, что решением системы (4) будут
 - не определено
и
- не определено
и
 =1;
=1;
системы (5) -
 = 1 и
= 1 и
 = 0;
= 0;
системы (6) -
 = 0 и
= 0 и
 = 1.
= 1.
Впишем
полученные значения
 и
и
 в таблицу 3, учитывая, что строки 0, 2, 4
и 1, 3, 7 имеют одинаковые значения
в таблицу 3, учитывая, что строки 0, 2, 4
и 1, 3, 7 имеют одинаковые значения
 и
и
 ,
в первом случае
,
в первом случае
 =
= =0,
во втором
=0,
во втором
 =
= =1.
=1.
Отметим, что решать рассмотренные характеристические уравнения можно и без составления таблицы, подобной таблице 5, однако для этого необходимы некоторые практические навыки.
Таким образом, в таблице 3 мы получили все значения функций возбуждения по входам бистабильной ячейки. Теперь по этим значениям нам необходимо получить логические уравнения, при помощи которых можно синтезировать входную логику.
Для этого
запишем уравнения для
 и
и
 ,
исходя из таблицы 3, аргументами для
этих уравнений будут служить переменные
автомата
,
исходя из таблицы 3, аргументами для
этих уравнений будут служить переменные
автомата
 ,
,
 ,
, :
:
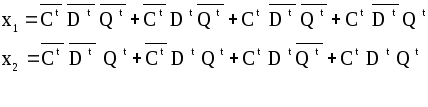
Составив карты Карно (рисунок 1), и оптимальным образом доопределив их на неопределенных наборах, получим

Рисунок 1 - Карты Карно функции возбуждения x>1> и x>2>
уравнения для функций возбуждения через аргументы автомата
 (7)
(7)
4) Переведем уравнения (7) в базис И-НЕ:
 (8)
(8)
Cделаем
следующие преобразования. Прибавим
(логическое сложение) к уравнению для
 значение
значение
 ;
от этого уравнение не изменится:
;
от этого уравнение не изменится:

Но
 равно
равно
 ,
тогда получим
,
тогда получим

Окончательно имеем:
 (9)
(9)
5) Строим
схему входной логики. Для этого изобразим
бистабильную ячейку И-НЕ, и на ее входы
 и
и
 подадим сигналы, соответствующие
уравнениям (9). Принципиальная схема
синхронного D-триггера представлена на
рисунке 2.
подадим сигналы, соответствующие
уравнениям (9). Принципиальная схема
синхронного D-триггера представлена на
рисунке 2.

а) Принципиальная схема б) Условное обозначение
Рисунок 2 - Принципиальная схема синхронного D-триггера
и его условное обозначение
Следует проверить, выполняет ли бистабильная ячейка И-НЕ функцию заданного автомата.
Для этого в
уравнение (2) подставим значения
 и
и
 из (8):
из (8):

Минимизируя последнее выражение, получим
 ,
,
что полностью соответствует уравнению (1).
Теперь осталось определить, как необходимо подавать установочные сигналы. Скажем сразу, что схема с установочными входами будет иметь вид, показанный на рисунке 3.

а) Принципиальная схема б) Обозначение на схеме
Рисунок 3 - Принципиальная схема синхронного D-триггера с установочными входами и обозначение на схеме
6) Составим
теперь таблицу переходов полученного
автомата. Для этого в уравнение (1) будем
подставлять различные значения
 и
и
 ,
т.е. переходы
,
т.е. переходы
 ,
и определять значение
,
и определять значение
 .Естественно,
при этом
.Естественно,
при этом
 =1.
=1.
Данные сведем
в таблицу переходов. В данном случае
можно не писать эти уравнения, так как
нам хорошо известно, что при
 =1
соблюдается уравнение
=1
соблюдается уравнение
 =
= ,
что хорошо иллюстрируется в таблице 6.
,
что хорошо иллюстрируется в таблице 6.

Таблица 6 - Таблица переходов
-
Qt Qt+1
Dt
0 0
0 1
1 0
1 1
0
1
0
1
Таким образом, мы полностью провели синтез синхронного автомата с одним информационным входом и двумя установочными входами R и S.
3 Описание лабораторного макета
На лицевой панели лабораторного стенда изображены схемы бистабильных ячеек типа ИЛИ-НЕ и И-НЕ и набор различных логических элементов, при помощи которых можно собрать различные автоматы на основе бистабильных ячеек. Коммутация логических элементов осуществляется при помощи соединительных проводов.
4 Программа работы
Для указанных преподавателем вариантов работы произвести полный синтез автомата, составить временную диаграмму работы устройства, проверить практически правильность функционирования синтезированного автомата, сверяясь с заданной таблицей работы.
5 Содержание отчета
Отчет должен содержать принципиальную схему полученного автомата, временную диаграмму его работы, все теоретические выкладки синтеза, таблицу переходов, логическое уравнение автомата.
6 Контрольные вопросы
6.1 Что называется конечным автоматом?
6.2 Опишите реакции последовательностного автомата на входные информационные входы.
6.3 Почему характеристические уравнения конечных автоматов должны быть полными?
6.4 Сколько различных последовательностных автоматов можно создать, если число его входов равно четырем?
6.5 Как из минимизированной таблицы функционирования конечного автомата получить его логическое уравнение?
6.6 Опишите вкратце этапы синтеза конечного автомата.
Список литературы
1. Алексенко А.Г., Шагурин И. И. Микросхемотехника. - М.: Радио и связь, 1990.
2.Скаржепа В.А., Луценко А.Н. Электроника и микросхемотехника. - Киев.: Выща школа, 1989.
3.Филиппов А.Г., Белкин О.С. Проектирование логических узлов ЭВМ. - М.: Советское радио, 1974.
4.Гусев В.Г., Гусев Ю.М. Электроника.- М.: Наука, 1990.
ЛАБОРАТОРНАЯ РАБОТА 4
АНАЛИЗ И СИНТЕЗ СЧЕТЧИКОВ
1 Цель работы
Изучить принципы работы счетчиков различных типов, овладеть методом синтеза синхронных счетчиков с различными коэффициентами пересчета на любых типах триггеров; приобрести навыки в построении принципиальных схем счетчиков при помощи временных диаграмм.
2 Краткая теория вопроса
2.1 Общие сведения
Счетчиком называется автомат, выполняющий функции подсчета количества импульсов единичных сигналов, поступивших на его вход, а также функции формирования и запоминания некоторого двоичного кода, соответствующего этому количеству. Другими словами - счетчик является преобразователем число-импульсного кода в некоторый двоичный код.
Помимо указанных функций счетчики иногда также могут выполнять функции приема и выдачи кода.
Входными сигналами счетчика являются или сигнал суммирующего или вычитающего счета, при этом одновременная подача этих сигналов запрещена.
В качестве выходной функции счетчика может быть задан сигнал переполнения, возникающий при суммировании, или сигнал заема возникающий при вычитании во время перехода счетчика через нуль.
Основным результатом работы счетчика является накопленный в нем код, определяемый состояниями элементарных автоматов.
Число элементарных автоматов (триггеров), необходимых для построения счетчика с заданным коэффициентом пересчета, равно числу его разрядов и определяется по формуле
m = log>2>N, (1)
где N - коэффициент пересчета (модуль, период счетчика) - максимальное число внутренних состояний, которое должен иметь счетчик. Очевидно, что это число равно максимальному числу входных сигналов, которое может сосчитать счетчик.
К другим важнейшим характеристикам счетчика относятся:
1) время регистрации - это интервал времени между поступлением входного сигнала и окончания самого длинного переходного процесса в схеме;
2) разрешающая способность - минимально допустимый период следования входных сигналов, при котором счетчик работает без сбоев.
2.2 Классификация счетчиков
Схемы счетчиков можно классифицировать по следующим признакам:
1) По основанию системы счисления счетчики делятся на:
а) двоичные ;
б) десятичные (двоично- десятичные);
Двоичные счетчики в свою очередь подразделяются на счетчики, модуль пересчета которых не равен 2m (где m - разрядность счетчика). Последние называются счетчиками по модулю М ( где М - число не кратное степени двойки ) .
2) По направлению переходов счетчики принято подразделять на:
а) суммирующие ;
б) вычитающие ;
в) реверсивные.
К последним относятся счетчики, способные выполнять операции суммирования и вычитания.
3) По способу построения цепей сигналов переноса различают счетчики:
а) с последовательным переносом ;
б) со сквозным переносом ;
в) с параллельным (сквозным) переносом ;
г) с частично групповым переносом .
4) По способу организации счета счетчики подразделяют на:
а) синхронные ;
б) асинхронные.
Время установки кода tуст является основным фактором, определяющим выбор способа переключения триггеров. При асинхронном способе tуст растет с увеличением числа триггеров (m) в счетчике, а при синхронном способе tуст не зависит от величины m.
Следует также учитывать, что с триггеров счетчика снимаемый параллельный код иногда подается на комбинационную схему (например, на дешифратор). В этом случае при асинхронном способе из-за неодновременного срабатывания триггеров счетчика возможно появление ложных логических сигналов на выходах комбинационной схемы.
Поэтому более предпочтительным, как правило, является синхронный способ организации счета, хотя при его использовании в счетчиках с большим числом триггеров (m>5..10) предъявляются повышенные требования к нагрузочной способности источников синхро-сигналов.
Асинхронный способ целесообразно применять в счетчиках, используемых в качестве делителей частоты.
Некоторые счетчики имеют цепи внешней установки начального состояния. Это состояние может также устанавливаться с помощью цепей обратной связи, имеющихся в самом счетчике. Кроме этого, счетчик может устанавливаться в начальное состояние после завершения одного цикла работы - подсчета числа входных сигналов, равного модулю счетчика.
2.3 Принцип работы счетчиков
Анализ схем счетчиков удобно начать с рассмотрения асинхронного двоичного счетчика с последовательным переносом (рисунок 1,а). Состояния триггеров счетчика после воздействия серии входных импульсов приведены в таблице 1. Временная диаграмма счетчика показана на рисунке 1,б.
Коэффициент пересчета этого счетчика
4 = log>2>Kсч; К>сч> = 24 = 16.
В качестве элементарного автомата используем Т-триггер. Эти счетчики характеризуются тем, что управляющими сигналами для старших разрядов являются сигналы, снимаемые с информационных выходов младших разрядов.
В исходном состоянии все триггеры устанавливаются в ноль (чтобы не загромождать чертеж, цепи сброса не показаны). В этом случае на нижних выводах всех триггеров устанавливается логическая еденица, а на верхних - логический ноль.
При поступлении импульса счета (рисунок 1,б) первый разряд подготовится к переключению и после окончания импульса перейдет в состояние Q = 1. Сигнал единица подается на вход второго триггера. После окончания действия второго счетного импульса на вход второго триггера поступит отрицательный перепад напряжения, так как первый триггер из состояния Q>1>=1 перейдет в состояние ноль.
Этот перепад напряжения вызовет изменение состояния второго триггера из нуля в единицу и на его выходе, а следовательно, на входе третьего триггера будет высокий потенциал. Сигнал Q>2>=1 подготавливает срабатывание третьего триггера. При поступлении семи импульсов установится состояние Q>1>=Q>2>=Q>3>=1, а восьмой импульс последовательно переключит все эти триггеры в состояние ноль и схема перейдет в первоначальное состояние.
Подобные счетчики являются простейшими по схемной реализации, но имеют невысокое быстродействие. Быстродействие счетчиков обычно характеризуется временем установки и максимальной частотой поступления счетных импульсов.
Максимальное время установки определяется временем перехода N - разрядного счетчика из кода 111...1, соответствующего заполнению счетчика, в код 000...0, соответствующий исходному состоянию. При этом должны последовательно сработать N триггеров и время установки будет равно t>уст>=N t>т>, t>т> - время переключения триггера.

Рисунок 1 - Двоичный счетчик на Т-триггерах
Максимальная частота поступления счетных импульсов определяется из выражения
f>cч >= 1/(t>имп >+ Nt>т>),
где t>имп> - длительность импульса.
В счетчиках с параллельным переносом счетные импульсы подаются на все разряды одновременно и изменение состояния данного разряда происходит только при определенном состоянии всех предыдущих триггеров. Структурная схема асинхронного счетчика с параллельным переносом показана на рисунке 2.

Рисунок 2 - Асинхронный счетчик на Т-триггерах с параллельным
переносом
Пусть в исходном состоянии в счетчике записан код 000. После первого счетного импульса сигнал Q>1> станет равным 1, при этом подготовится к срабатыванию схема совпадения 1. Второй счетный импульс вернет Q>1> в исходное состояние и через схему совпадения 1 пройдет на триггер второго разряда. Схема совпадения 2 закрыта, так как Q>1>=0. Таким образом, после второго счетного импульса установятся состояния Q>1>=0, Q>2>=1, Q>3>=0, Q>4>=0. После третьего счетного импульса в счетчике будет зафиксирован код 0011. Теперь в состоянии, открытом для прохождения счетных импульсов будут находиться обе схемы совпадения. В результате четвертый импульс поступит на все три разряда и установит счетчик в состояние 0100, и так далее.
На рисунке 3 показана функциональная схема синхронного двоичного счетчика со сквозным переносом.
Здесь входной сигнал подается одновременно на входы с всех разрядов счетчика. Переключение каждого i-го Т-триггера возможно в том случае, если на его информационном входе Т>i> присутствует сигнал (логическая единица). Если Т>i>=0, то триггер находится в режиме запоминания.
Так как на вход триггера младшего разряда счетчика подана логическая единица, то он работает как асинхронный триггер со счетным входом, т.е. изменяет свое состояние на противоположное под воздействием каждого входного сигнала (счетного импульса). Изменение состояний триггера старших разрядов счетчика возможно только в том случае, если все предшествующие триггеры младших разрядов находятся в состоянии 1.

Рисунок 3 - Синхронный двоичный счетчик со сквозным переносом
Длительность переходного процесса в таком счетчике зависит от разрядности счетчика в меньшей степени, чем у счетчика с последовательным переносом, и определяется временем задержки сигнала в элементах И в цепях сквозного переноса.
На рисунке 4 изображена функциональная схема счетчика с параллельным переносом. Отличительной особенностью данной схемы является то, что выходы всех предшествующих Q> n-k> разрядов подаются на информационные входы J и К n-го триггера.

Рисунок 4 - Синхронный двоичный счетчик с параллельным переносом
Длительность переходного процесса в таком счетчике равна длительности переключения одного разряда. Из схемы видно, что с возрастанием порядкового номера триггера увеличивается число входов в клапаны "И" JK - триггеров. А так как число входов J и К в любой реальной схеме элементов конечно, а нагрузочная способность выходов триггеров ограничена, то и разрядность счетчика с параллельным переносом невелика и равна обычно четырем. Поэтому при числе разрядов счетчика большем максимального числа входов J и К счетчик разбивают на группы и внутри каждой группы строят цепи параллельного переноса. Перенос между группами реализуется методом сквозного переноса. Такой способ образования сигналов переноса называется групповым. Счетчики с параллельными и групповыми переносами являются наиболее быстродействующими.
2.4 Синтез двоичных счетчиков
Синтез счетчика сводится к определению оптимальной в некотором смысле структуры и в конечном счете построению его принципиальной схемы.
Здесь под оптимальной понимается структура счетчика, содержащая минимальное число триггеров и связей между ними, при которой обеспечивается выполнение счетчиком требуемых функций с заданными значениями параметров.
Основными исходными данными для синтеза счетчика, вытекающими из его назначений, являются:
1) модуль счета ( емкость счетчика );
2) порядок изменения состояний счетчика ;
3) режим счета для счетчиков с естественным порядком изменения состояний (суммирующий, вычитающий, реверсивный);
4) требуемая разрешающая способность счетчика t>p>;
5) необходимое время установки кода счетчика t>уст>.
Рассмотрим синтез трехразрядного двоичного суммирующего в коде 8421 счетчика с N=8 на JK - триггерах 155 серии. Этот триггер К155ТВ1 (рисунок 5) имеет три входа J (ЗИ) и три входа К (ЗИ), а также вход С для подачи синхросигнала. Кроме того, триггер имеет дополнительные нетактируемые входы R и S для предварительной установки триггера соответственно в нулевое и единичное состояния.
Универсальный JK - триггер описывается характеристическим уравнением
 ,
,
где J>i > и K>i> - логические функции J и К, соответствующие предыдущему состоянию триггера Q>i> ;
Q*>i> - будущее состояние триггера.

Рисунок 5 - Триггер JK - типа
Таблица 1 - Переходы Таблица 2 - Функционирование
триггера счетчика


Характеристическая таблица JK - триггера, в которой приводятся обобщенные значения логических функций на его входах для всех возможных комбинаций имеет следующий вид (таблица 2). Звездочками отмечены неопределенные значения входных сигналов.
Количество триггеров в таком счетчике должно быть равно трем согласно формуле (1). Условия переходов для данного счетчика приведена в таблица 1.
На основе таблицы функционирования счетчика для каждого триггера составляются карты Карно, отражающие переходы данного триггера из предыдущего состояния Q>i> в последующее состояние Q*>i>.
Для того, чтобы в клетках карты Карно зафиксировать состояния триггеров запишем трехразрядные двоичные числа, как показано на рисунке 6,а. В эквивалентном десятичном коде эти числа будут иметь изображение, показанное на рисунке 6,б.
Если в клетки карты Карно (рисунок 6), соответствующие номерам предыдущих состояний счетчика (0,1,2, .... 7) вписать двухразрядные двоичные числа, выражающие переход триггера Q>i> --- Q*>i> при изменении состояния счетчика, то получим так называемые прикладные таблицы.
Из таблицы функционирования счетчика (таблица 2) отмечаем, что для триггера Q>1> переход из нулевого состояния (нулевая строка таблицы) в единичное состояние

Рисунок 6 - Карты Карно, заполненные двоичными числами и эквивалентными десятичными числами, соответствующими состояниями счетчика
осуществляется как Q0>i >-- Q1>i >= 0 —- 1 или 01. Следовательно, в клетку карты Карно с номером 0 (рисунок 6,б) следует записать число 01. Рассматривая переход триг-

Рисунок 7 - Прикладные таблицы Карно для счетчика с N=8
гера Q>1> из единичного в нулевое состояние (первая строка таблицы), видно что переход осуществляется как Q1>i>> >—- Q0>i>> >= = 1 —- 0 или 10.
Тогда в клетку карты с номером 1 (рисунок 6,б) записываем двоичное число 10. Аналогичным образом заполняются и другие клетки карты.
Переходы всех триггеров, выраженные двузначными двоичными числами, запишем в соответствующие клетки с номерами состояний прикладных таблиц (рисунок 7).
Преобразуем полученные таблицы Карно в соответствии с характеристической таблицей JK - триггера (таблица 1). Для этого в клетки прикладных таблиц запишем вместо двоичных чисел (00,01,10 и 11) значения информационных входов J и К, соответствующие определенным переходам Q>i> --- Q*>i>.
Так, например, для информационных входов Ji триггеров Q>1>,Q>2>,Q>3 >карты Карно будут выглядеть следующим образом, как показано на рисунке 8.

Рисунок 8 - Карты Карно, характеризующие информационные входы триггеров счетчика с N=8
После склеивания единиц получим уравнения информационных входов
J>1 >= 1 ; J>2 >= Q>1> ; J>3 >= Q>1>Q>2>.
Аналогичным образом строятся карты и для информационных входов K>i >(рисунок 9), откуда получим следующие уравнения
K>1>=1 ; K>2>=Q>1> ; K>3>=Q>1>Q>2>

Рисунок 9 - Карты Карно, характеризующие информационные входы триггеров счетчика с N=8
Таким образом, для суммирующего счетчика с N=8 имеем следующую систему уравнений информационных входов триггеров
J>1>=K>1>=1;
J>2>=K>2>=Q>1>;
J>3>=K>3>=Q>1>Q>2>.
Исходя из полученных уравнений, построим схему счетчика, показанную на рисунке 10.
В вычитающем счетчике номер последующего состояния должен быть на единицу меньше номера предыдущего состояния. В остальном синтез такого счетчика производится по приведенной методике.
На рисунке 11 показана схема вычитающего счетчика с N=8, в котором информационные входы триггеров описываются уравнениями
 .
.

Рисунок 10 - Схема суммирующего счетчика на JK-триггерах

Рисунок 11 - Синхронный вычитающий счетчик с N=8
Реверсивный счетчик осуществляет счет сигналов как в режиме сложения, так и в режиме вычитания. Режим работы счетчика изменяют с помощью схемы управления. В зависимости от требований к схеме управления можно построить реверсивные счетчики двух типов. Первый имеет один счетный и два управляющих входа, а второй - два счетных входа. Для последних не требуются специальные управляющие сигналы.
Рассмотрим синтез синхронного реверсивного счетчика первого типа. В этом случае для каждого режима счета определяют функции J и К - входов всех триггеров. Затем синтезируют схему управления. Пусть N=8. Дадим без вывода уравнения логических входов J и К суммирующего счетчика с указанным коэффициентом пересчета
J>1>=K>1>=1 ; J>2>=K>2>=Q>1> ; J>3>=K>3>=Q>1>Q>2>.
Для вычитающего счетчика с N=8 воспользуемся результатами, полученными при предыдущем синтезе
 (1)
(1)
Отсюда следует, что при изменении счета функции на управляющих входах первого триггера не изменяются (J>1>=K>1>=1), а логические переменные, входящие в функции J и К - входов второго и третьего триггеров, меняются на инверсные. Поэтому для реверсирования счета необходимо произвести коммутацию входов первого и второго триггеров счетчика. Эта коммутация осуществляется с помощью сигнала управления Т, принимающего значения "I" и "0" в зависимости от задаваемого направления счета. Тогда логические уравнения, описывающие работу схемы управления, имеют следующие очевидные выражения

Действительно, при Т=1 обеспечивается режим сложения, а при Т=0 - режим вычитания.
Полученные выражения можно реализовать с помощью логических элементов И-ИЛИ-НЕ. Для этого преобразуем выражение (2) к следующему виду
 .
.
Cоответственно выражение (3) после проведения тождественных преобразований примет вид
 .
.

Рисунок 12 - Схема реверсивного счетчика с N=8
Как следует из полученных уравнений, элементы схемы управления, находящиеся между соседними триггерами, имеют идентичную структуру.
Схема реверсивного счетчика, построенного на триггерах 155 серии и логических элементах И-ИЛИ-НЕ, приведена на рисунке 12.
2.4 Синтез двоичного счетчика с произвольным порядком счета
Исходными данными для синтеза такого счетчика является порядок перехода счетчика из одного состояния в другое после передачи очередного входного сигнала.
Общее число устойчивых состояний двоичного счетчика с произвольным порядком счета равно коэффициенту пересчета N=2m, а возможное число вариантов схем, отличающихся друг от друга порядком смены состояний определяется величиной (N-1)!. Для N=8 существует 5040 вариантов схем.
Рассмотрим синтез двоичного счетчика с произвольным порядком счета и N=8 с использованием JK - триггера 155 серии.
Пусть смена состояний счетчика будет

Составим таблицу функционирования счетчика (таблица 4)
Исходя из таблицы функционирования счетчика для каждого триггера составим прикладные таблицы (рисунок 13).
Таблица 3 - Функционирование счетчика с N = 8


Рисунок 13 - Прикладные таблицы триггеров счетчика с произвольным порядком счета
Используя характеристическую таблицу JK-триггера (таблица 2),преобразуем прикладные таблицы в карты информационных входов J>i >и K>i> (рисунок 14).
На рисунке 15 представлена схема счетчика, построенного по полученным уравнениям.
2.5 Синтез недвоичных счетчиков
Недвоичные счетчики имеют N = 2m. Принцип их построения состоит в исключении некоторых устойчивых состояний обычно двоичного счетчика, являющихся избыточными для недвоичного счетчика. Избыточные состояния исключаются с помощью обратных связей внутри счетчика. Обратные связи образуют введением дополнительных логических цепей, соединяющих входы и выходы соответствующих триггеров.

Рисунок 14 - Карты Карно информационных входов триггеров счетчика с произвольным порядком счета

Рисунок 15 - Схема счетчика с N = 8 произвольным порядком счета
Из карт Карно имеем следующие уравнения информационных входов триггеров
 .
.
Задача синтеза недвоичного счетчика сводится к определению необходимых обратных связей и минимизации их числа. Количество триггеров в недвоичном счетчике определяется из выражения
m = [log>2>N],
где [log>2>N] - двоичный логарифм заданного коэффициента пересчета N, округленный до ближайшего большего целого числа.
Число исключаемых избыточных состояний равно
К = 2m - N.
Поскольку можно исключить любые состояния в любых комбинациях, то общее число схем недвоичного счетчика с одним и тем же N и всеми вариантами изменения порядка счета определяется величиной
 .
.
В общем случае выбор исключаемых состояний определяется назначением недвоичного счетчика.
Рассмотрим пример построения синхронного счетчика с N=3 на JK триггерах 155 серии.
Он строится на основе двоичного счетчика, состоящего из двух триггеров, так как
m = [log>2>N] = [log>2>3] = 1,58 =2.
Число избыточных состояний счетчика равно
K = 2m - 3 = 1.
Из возможных состояний счетчика (00,01,10,11) исключаем, например, состояние Q>1>Q>2>. Порядок изменения состояний примем следующий
 .
.
Таблица 4 - Функционирование счетчика с N = 3

Составим таблицу функционирования счетчика (таблица 5), на основании которой составляем прикладные таблицы триггеров и производим преобразование их в карты Карно информационных входов J>i >и K> i >(рисунок 16).
Исключенное состояние в прикладных картах и картах Карно отмечаем черточкой.

Рисунок 16 - Прикладные таблицы и карты Карно информационных входов JK-триггеров счетчика с N=3
Из карт Карно имеем следующие уравнения информационных входов:


Рисунок 17 - Синхронный счетчик с N=3
Таким образом, для построения недвоичного синхронного счетчика с К>сч>=3 необходимо J - вход первого триггера соединить с инверсным выходом второго триггера, а J - вход последнего соединить с прямым выходом первого триггера. На К - входы обоих триггеров необходимо подать постоянный потенциал, соответствующий логической единице. Схема счетчика показана на рисунке 17.
Аналогичным образом строятся синхронные счетчики с другими недвоичными коэффициентами пересчета.
2.6 Синтез двоично - десятичных счетчиков
Среди недвоичных счетчиков в отдельный класс выделяют двоично - десятичные счетчики с N=10, которые строятся на основе четырех триггерных двоичных счетчиков исключением шести состояний.
В разных вариантах схем одним и тем же десятичным числам могут соответствовать различные четырехразрядные кодовые комбинации в зависимости от исключенных состояний. Иными словами такие счетчики работают в различных двоично - десятичных кодах.
Существует большое число двоично - десятичных кодов, часть из которых приведена в таблице 5. Особую группу составляют самодополняющиеся коды. Характерной особенностью этих кодов является соответствие обратных двоичных чисел обратным десятичным числам.
Порядок синтеза синхронных двоично-десятичных счетчиков принципиально не отличается от синтеза недвоичных счетчиков. Разница заключается лишь в том, что выбор комбинации шести исключаемых состояний определяется исходя из двоично - десятичного кода, в котором должен работать счетчик.
В качестве примера рассмотрим синтез счетчика, работающего в коде 8421, или коде прямого замещения.
Согласно таблице 6 при работе двоично - десятичного счетчика в указанном коде необходимо исключить состояния
 .
.
Таблица 5 - Кодирование десятичных чисел

Составим таблицу переходов триггеров (таблица 6).
Построим прикладные таблицы и карты Карно для входов J>i> и K>i> всех триггеров счетчика (рисунок 18), используя таблицу функционирования счетчика (таблица 6) и характеристическую таблицу JK - триггера (таблица 2). Избыточные состояния в таблицах и картах Карно отметим черточкой.
После минимизации получим следующие уравнения информационных входов JK-триггеров счетчика
 .
.
Таблица 6 - Переходы триггеров

Согласно этим уравнениям построим схему счетчика (рисунок 19).

Рисунок 18 - Прикладные таблицы и карты Карно информационных триггеров двоично-десятичного счетчика

Рисунок 19 - Двоично - десятичный счетчик, работающий в коде 8421
Отметим, что для построения различных типов синхронных счетчиков с использованием универсальных JK-триггеров с тремя входами J и К структура счетчика получается достаточно простой, если число триггеров не превышает четырех. При его увеличении целесообразно объединить триггеры в группы, каждая из которых содержит не более четырех триггеров. Группы соединяют между собой последовательно. При этом последний триггер предыдущей группы является источником синхросигналов для последующей. С помощью такого включения обеспечивается синхронный режим внутри каждой группы и последовательная передача информации от группы к группе. По быстродействию счетчики с такими связями занимают промежуточное положение между синхронными и асинхронными.
3 Описание лабораторного макета
Лабораторное устройство представляет собой набор JK - триггеров и логических элементов серии 155. На наборное поле макета выведены входы и выходы ИМС, что позволяет коммутировать любые схемы счетчиков.
Внутри макета смонтирован генератор, который может выдавать как непрерывные, так и одиночные прямоугольные импульсы. Кроме того предусматривается подача высокого (единичного) уровня напряжения и низкого (нулевого) уровня.
На выходах Q всех триггеров установлены лампочки, фиксирующие состояния триггеров. Отдельная контрольная (КОН) лампочка служит для определения выходного сигнала при подаче на вход счетчика одиночных импульсов.
4 Содержание и порядок работы
4.1 Построить реверсивный четырехразрядный счетчик с N=12.
4.2 Построить реверсивный десятичный счетчик, считающий в самодополняющемся коде 4221.
4.3 Построить счетчик , считающий в коде Грея .
4.4 Построить счетчик, считающий в коде Джонсона (0000,0001,0011,0111,1111,1110,1100,1000).
4.5 Построить десятичный счетчик, считающий в коде с избытком 3.
4.6 Построить счетчик в следующем коде 0001,0011,0101,0111,1001,0010,0100,0110,1000,0001 .
5 Содержание отчета
Отчет должен содержать :
5.1 Краткие теоретические сведения, необходимые для выполнения задания .
5.2 Все схемы, формулы, таблицы, карты Карно, полученные при выполнении работы.
5.3 Временные диаграммы исследуемых счетчиков.
5.4 Выводы по работе.
6 Контрольные вопросы
6.1 Перечислить основные признаки классификации счетчиков.
6.2 Как можно установить в счетчике исходное состояние?
6.3 Чем отличается вычитающий счетчик от суммирующего?
6.4 Сколько триггеров необходимо для счетчика с Ксч=8567?
6.5 Какой порядок счета называется естественным, а какой искусственным?
6.6 В чем состоят принципы работы последовательного, сквозного, параллельного и группового переносов, их достоинства и недостатки?
6.7 Сколько корпусов четырехразрядных микросхем двоичных счетчиков надо для Ксч = 1283 и 3600?
6.8 Чем отличаются двоичные и двоично - десятичные счетчики?
6.9 Какая особенность у счетчика Джонсона?
Список литературы
1.Гусев В.Г.,Гусев Ю.М. Электроника.- М.: Наука, 1990.
2.Шило В.Л. Популярные цифровые микросхемы. - Челябинск.: Металлургия, 1989.
3.Потемкин И.С. Функциональные узлы цифровой автоматики. - М.: Энергоиздат , 1988.
4.Алексенко А.Г., Шагурин И.И. Микросхемотехника .- М.: Радио и связь, 1990.
5.Агаханян Т.М. Интегральные микросхемы. - М.: Энергоатомиздат, 1983.
ЛАБОРАТОРНАЯ РАБОТА 5
ИССЛЕДОВАНИЕ МУЛЬТИПЛЕКСОРА
1 Цель работы
Целью данной работы является изучение принципа работы мультиплексора; его возможностей при реализации булевых функций с относительно большим числом аргументов (переменных), а также приобретение практических навыков схемотехнических решений при реализации с помощью мультиплексора конкретных логических уравнений, включая комбинационные схемы с несколькими выходами. Рекомендуется ознакомиться с параметрами различных типов мультиплексоров, выпускаемых отечественной промышленностью.
2 Краткая теория вопроса
2.1 Общие сведения
В настоящее время в составе различных серий микросхем, например, 155, 531, 555, 1533, 1534, выпускаются схемы средней степени интеграции - мультиплексоры (коммутаторы).
Они выполняют функцию выбора данных от одного из нескольких источников информации, поступающих на его входы и, таким образом, являются электронным аналогом широко известного электромеханического шагового искателя.
Мультиплексор представляет собой многовходовой логический элемент комбинационного типа, как правило, с одним выходом.
Основные типы мультиплексоров подразделяются на два типа:
1) информационные (обозначаются как x>i>, D>i>);
2) управляющие (иначе - селекторные, адресные).
Между числом этих входов существует определенная математическая связь. Если имеется n управляющих входов, то максимальное число информационных входов составляет только 2n. Каждому из 2n информационному входу соответствует только одна двоичная комбинация на управляющих входах. Другими словами, при подаче на управляющие входы соответствующего сигнала в виде двоичного кода к выходу мультиплексора подключится только один из 2n информационных входов, строго соответствующий заданному управляющему коду на управляющих входах. Например, если в мультиплексоре, имеющем три управляющих входа, на них будет код 101, то к выходу его подключится только пятый (101<=>5) из восьми возможных информационных входов(23=8).
Отметим, что некоторые мультиплексоры , например К155КП7, имеют два выхода, при этом один из них соответствует инвертированному значению заданной функции, другой - прямому.
Кроме указанных входов мультиплексор имеет еще стробирующий вход, который позволяет значительно расширить их функциональные возможности.
И, наконец, в некоторых сериях, например К1533КП15, имеется вход управления установки выходов мультиплексора в третье состояние (обозначается как EZ).
Отечественная промышленность выпускает в настоящее время мультиплексоры, осуществляющие выбор одного из 4-х, 8-ми и 16-ти информационных каналов (входов); они различаются числом адресных входов:
4х1 (два управляющих входа);
8х1 (три управляющих входа);
16х1 (четыре управляющих входа).
Мультиплексоры с четырьмя информационными входами (КП155КП2, КР1533КП2) обычно изготавливают по два на одном кристалле. При этом адресные входы к ним являются общими. Выборка одного из мультиплексоров осуществляется по стробирующему входу. Одновременно оба мультиплексора в таком исполнении работать не могут. Такое конструктивное решение оказывается очень удобным при логическом проектировании схем управления.
Мультиплексоры помимо выполняемой ими непосредственно заданной функции селектирования, оказываются весьма удобными логическими элементами при создании различных комбинационных схем.. Хотя стоимость мультиплексора выше стоимости логических схем малой степени интеграции, применение мультиплексоров часто позволяет уменьшить требуемое число корпусов и число соединений между ними. А стоимость и надежность цифровых устройств в основном определяется, как известно, стоимостью и надежностью соединений.
Таким образом, основными достоинствами использования мультиплексоров в комбинационных схемах являются:
1) сокращение числа соединений и объема пайки;
2) уменьшение стоимости элементов и монтажа;
3) повышение надежности схемы.
К недостаткам можно отнести:
1) трудности перестройки схем на печатных платах.
2.2. Структура мультиплексоров
На рисунке 1 показаны условные обозначения мультиплексоров, взятые из разных справочников.
Здесь
 - информационные входы;
- информационные входы;
 - управляющие (адресные, селекторные)
входы; E, V,S,- вход стробирования;
- управляющие (адресные, селекторные)
входы; E, V,S,- вход стробирования;
 - выходы.
- выходы.
Принципиальная схема мультиплексора 8х1 (К155КП7) показана на рисунке 2.
Если сопоставить эту схему с другими подобными по структуре комбинационными схемами, то легко убедиться, что здесь явная аналогия со схемой дешифратора на восемь выходов, с небольшой, с точки зрения схемотехники, разницей, а именно - в мультиплексоре все восемь выходов элементов И объединяются элементом ИЛИ.
Согласно принципиальной схеме уравнение мультиплексора 8х1 может быть записано в виде

Заметим, что в уравнении не используется вход стробирования. Для нашего анализа это не имеет существенного значения.
Подставляя
вместо
 их двоичные эквиваленты, уравнение (1)
можно представить как
их двоичные эквиваленты, уравнение (1)
можно представить как
 .
.

Рисунок 1 - Условные изображения мультиплексоров

Рисунок 2 - Принципиальная схема мультиплексора К155КП7
Аналогично можно записать логическое уравнение любого другого типа мультиплексора, например, для мультиплексора 4х1 уравнение будет таким
 (2)
(2)
или
 .
.
Отметим, это важно, что уравнение (1) можно представить и так
 (3)
(3)
Теперь интересно сравнить оба слагаемых в скобках уравнения (3) мультиплексора 8х1 с уравнением (2) мультиплексора 4х1.
2.3 Реализация булевых функций при помощи мультиплексора
Рассмотрим идею реализации мультиплексором булевых функций и покажем, что мультиплексор является универсальным логическим элементом.
Для этого рассмотрим логическую функцию, реализуемую мультиплексором на четыре канала, изображенном на рисунке 3.

Рисунок 3 - Мультиплексор на четыре канала
Запишем уравнение мультиплексора

или
 .
.
Покажем,
что любая трехместная функция f( )
может быть реализована этим мультиплексором.
Используя метод функциональной
декомпозиции (теорему Шеннона), функцию
f(
)
может быть реализована этим мультиплексором.
Используя метод функциональной
декомпозиции (теорему Шеннона), функцию
f( )
представим в виде
)
представим в виде
 .
.
Применяя к полученному выражению еще раз теорему Шеннона, будем иметь
 .
.
Сопоставим теперь фрагменты полученного уравнения функции с переменными, являющимися аргументами функции, реализуемой мультиплексором на четыре канала, т.е.:
 ,
,
 .
.
Наглядно
видно, что эти уравнения подобны. Для
полной тождественности их примем
 ,
и тогда должно быть
,
и тогда должно быть

Рассмотрим
первое слагаемое функции f( ).
Оно может соответствовать двум точкам
гиперкуба,
).
Оно может соответствовать двум точкам
гиперкуба,
 , т.к.
, т.к.
 может принимать значения 0 или 1:
может принимать значения 0 или 1:

При этом
возможны следующие четыре пары значений
функции f( )
в зависимости от того, какие значения
может принимать и сама функция (вспомним
сингулярную функцию),т.е.:
)
в зависимости от того, какие значения
может принимать и сама функция (вспомним
сингулярную функцию),т.е.:

Тогда для каждой пары будем иметь:
для первой
пары f(0,0, )=0,
поэтому
)=0,
поэтому
 =0;
=0;
для второй
пары f(0,0, )=
)=
 ,
поэтому
,
поэтому
 =
= ;
;
для третьей
пары f(0,0, )=
)= ,
поэтому
,
поэтому
 =
= ;
;
для четвертой
пары f(0,0, )=1,
поэтому
)=1,
поэтому
 =1.
=1.
Таким образом, для реализации булевой функции трех переменных на мультиплексоре 4х1 необходимо две переменные заданной функции, например x>1 >и x>2,> подать на адресные входы А>1 >и А>2>, а третью переменную x>3> подать тем или иным способом на информационные входы D>0>, > >D>1>, D>2>, D>3 >мультиплексора.
Чтобы хорошо разобраться в способах реализации булевых функций на мультиплексорах, рассмотрим несколько примеров.
Пример 1. Разберем вначале элементарную задачу. Пусть требуется реализовать на мультиплексоре 8х1 функцию
 .
.
Решение. Изобразим эту функцию в виде таблицы истинности (таблица 1), в которой переменные х>1>, х>2>,х>3> уравнения заменим адресными входами А>1>, А>2>, А>3>.
Из этой таблицы следует, что в соответствии с кодами адресных входов на информационные входы D>0 >- D>7> необходимо подавать только логические 0 и 1 согласно значениям заданной функции F, а именно, на входы D>0>, D>2>,D>3>, D>6>,D>7 >нужно подать высокий потенциал (“1”), а на входы D>1>,
Таблица 1 - Таблица истинности
-
N(D>i>)
A>1>(x>1>)
A>2>(x>2>)
A>3>(x>3>)
F
D>i>
0
0
0
0
1
1
1
0
0
1
0
0
2
0
1
0
1
1
3
0
1
1
1
1
4
1
0
0
0
0
5
1
0
1
0
0
6
1
1
0
1
1
7
1
1
1
1
1
D>4>,D>5 >- низкий (“0”), т.е. заземлить. Для того, чтобы мультиплексор работал, вход “строб” (S) также нужно заземлить. Схема реализации показана на рисунке 4.

Рисунок 4 - Схема реализации примера 1
Пример 2. Реализовать на мультиплексоре 4х1 функцию
 .
.
Решение.
1 этап. Выберем мультиплексор типа К155КП2 (рисунок 5), таблица функционирования для одной половинки которого имеет вид (таблица 2).
Согласно
таблице истинности микросхемы К155КП2
имеем, что
 соответствует информационному входу
D>0>;
соответствует информационному входу
D>0>;
 -
D>1>;
-
D>1>;
 - D>2>;
- D>2>;
 -D>3>.
-D>3>.
Таблица 2 - Таблица истинности К155КП2
-
Входы
Выход
1S
A>1>
A>2>
D>0>
D>1>
D>2>
D>3>
F>i>
0
0
0
0
1
0
0
1
1
x
0
1
0
1
x
1
0
0
0
x
0
1
0
0
x
0
0
1
0
x
0
0
0
1
x
1
1
1
1
0

Рисунок 5 - Мультиплексор К155КП2
2 этап. Строим таблицу истинности заданной функции и анализируем ее в соответствии с имеющимися данными (таблица 3).
Определяем информационные входы D>0 >- D>3> в соответствии с кодами управляющих сигналов A>1> A>2 >(таблица 2).
Определяем функции возбуждения информационных каналов мультиплексора, т.е. какие сигналы и на какие входы нужно подать, учитывая, что х>1 >и х>2> поданы на A>1> и A>2> соответственно.
Таблица 3 - Совмещенная
|
A>1> |
A>2> |
х>3> |
F |
D>i> |
N |
|
|
0 0 |
0 0 |
0 1 |
0 1 |
x>3> |
0 1 |
D>0> |
|
0 0 |
1 1 |
0 1 |
1 0 |
|
2 3 |
D>1> |
|
1 1 |
0 0 |
0 1 |
1 0 |
|
4 5 |
D>2> |
|
1 1 |
1 1 |
0 1 |
0 0 |
0 |
6 7 |
D>3> |

Рисунок 6 - Схема реализации примера 2
Для этого рассмотрим строки 0 и 1 таблицы истинности функции (таблица 3). Имеем

Так как
х>3>
в этих строках повторяет значение
функции F, то
 =
= .
.
Из 2-й и 3-й строки таблицы следует

Так как
х>3>
в этих строках является инверсией
функции F, то следует, что
 =
= .
.
Из 4-й и 5-й строки следует, что

Отсюда
 =
= .
.
Из последних двух строк очевидно, что D>3>=0.
3 Этап. Строим принципиальную схему, которая показана на рисунке 6.
Наличие в мультиплексоре стробирующего входа позволяет, как было сказано выше, значительно расширить его логические возможности. Для иллюстрации этого положения рассмотрим уравнения мультиплексоров 4х1 и 8х1 :
 .
.

Как видно из сопоставления этих уравнений, выражения в скобках уравнения для мультиплексора 8х1, являются уравнениями, аналогичными уравнению мультиплексора 4х1. Мультиплексор 8х1 может реализовать любую булеву функцию четырех переменных с минимальным числом внешних элементов, что невозможно осуществить на одном мультиплексоре 4х1. Но, используя два мультиплексора 4х1 со стробирующими входами, операцию реализации функции четырех переменных легко можно осуществить, подавая на входы S переменную A>3 >со своими значениями, заданными в функции. Этот сигнал будет попеременно подключать в работу первый или второй мультиплексор.
Аналогично можно получить и следующие связи между мультиплексорами

Отметим, что при числе переменных больше трех, следует пользоваться не таблицами истинности из-за их громоздкости, а картами Карно.
3 Описание лабораторного устройства
На лицевой панели лабораторного макета показаны два мультиплексора типа К155КП2 и наборы логических элементов. Имеются гнезда с высокими и низкими уровнями напряжения, имитирующие сигналы логической единицы и логического нуля. Коммутация схемы производится при помощи набора соединительных проводов.
4 Программа работы
По заданному варианту синтезировать и начертить схему, реализующую заданную булеву функцию при помощи одного или (и) двух мультиплексоров. До набора схемы на макете показать расчеты преподавателю.
5 Содержание работы
Отчет должен содержать:
5.1 задания согласно выданному варианту;
5.2 подробный синтез схемы;
5.3 принципиальные схемы по каждой заданной функции.
6 Контрольные вопросы
6.1 Чем отличается мультиплексор от дешифратора?
6.2 Какие функции может выполнять стробирующий вход?
6.3 Напишите уравнение мультиплексора 16x1 для реализации его на мультиплексорах 8x1.
6.4 Опишите работу демультиплексора.
Список литературы
1. Шило В.Л. Популярные цифровые микросхемы.- Челябинск.: Металлургия, 1989.
2. Алексенко А.Г., Шагурин И.И. Микросхемотехника. -М.: Радио и связь, 1990.
3. Скаржепа В.А., Луценко А.Н. Электроника и микросхемотехника.- Киев.: Выща школа, 1989.
4. Применение интегральных микросхем в электронной вычислительной технике / Под ред. Б.В. Тарабрина.- М.: Радио и связь, 1987.
5.Зельдин Е.А. Цифровые интегральные микросхемы в информационно-измерительной аппаратуре.- Л.: Энергоатомиздат, 1986.
6. Голдсуорт Б. Проектирование цифровых логических устройств. - М.: Машиностроение, 1985.
ЛАБОРАТОРНАЯ РАБОТА 6
ИССЛЕДОВАНИЕ ТАЙМЕРА
1 Цель работы
Цель данной работы состоит в ознакомлении с параметрами таймера КР1006ВИ1, принципом его работы и схемотехническими решениями при построении таймеров заданных типов, а также в приобретении практических навыков расчетов таймеров, изучении принципиальной схемы классического (базового) таймера и временных диаграмм его работы.
2 Теория вопроса
2.1 Общие сведения
Полупроводниковые таймеры - это относительно новый вид функционального элемента в микроэлектронике.
Впервые таймер (NE 555) был выпущен фирмой Signetics Corporation в 1972 году. Появление отечественного аналога таймера КР1006ВИ1 дало возможность использовать его для проектирования большинства схем установки времени, при этом используется лишь несколько внешних элементов и, таким образом, существенно упрощается проектирование. Таймер КР1006ВИ1 с такими достоинствами, как простота, универсальность и экономичность, быстро приобрел широкую популярность, сравнимую с популярностью операционных усилителей.
По функциональному составу внутренних узлов и способу выполнения заданной функции таймеры не являются полностью аналоговыми или цифровыми ИС.
Современные таймеры наряду с компараторами напряжения, которые относят к аналоговым ИС, содержат узлы, выполняющие цифровые функции - логические вентили, триггеры счетчики и др. Компараторы в таймерах обеспечивают повышение чувствительности цифровых структур от единиц вольт до долей милливольта к изменениям входных напряжений. Таким образом, основные функции в таймерах выполняют цифровые узлы, точность же формирования времени определяется в первую очередь компараторами напряжения.
2.2 Назначения таймеров
В цифровых схемах часто требуется источник импульсов с точно определенной длительностью. Обычно необходимы :
1) Одиночный импульс с заданной длительностью;
2) Непрерывная последовательность импульсов с заданными:
а) частотой;
б) коэффициентом заполнения или скважностью.
Первому требованию удовлетворяет моностабильная схема, а второму - астабильная. Таймер может работать в обоих режимах, а для задания его рабочих параметров требуется очень мало внешних элементов.
Таймеры также используются для синхронизации и для различных видов импульсной модуляции.
Таймеры могут быть классифицированы по двум основным категориям:
1) Однотактные таймеры типа одновибраторов;
2) Многотактные таймеры или таймеры / счетчики.
Однотактные таймеры оперируют зарядом источника времязадающего тока, тогда как таймеры / счетчики совмещают генератор базового времени с каскадом счетчика для получения длительных задержек.
2.3 Функциональная схема таймера
Упрощенное внутреннее устройство таймера КР1006ВИ1 приведено на рисунке 1.а, условное его обозначение показано на рисунке 1.б, а принципиальная схема - на рисунке 2.
Эта микросхема состоит из двух операционных усилителей, используемых в качестве компараторов К1 и К2, RS - триггера, делителя напряжения состоящего из трех резисторов R1 - R3 по 5кОм каждый. Кроме того предусмотрен инвертирующий выходной каскад, обеспечивающий достаточно высокую нагрузочную способность. Для быстрого разряда внешнего времязадающего конденсатора имеется транзисторный ключ Т11, а для сброса таймера используется блокирующий транзистор Т10

а) Функциональная схема

б) Условное обозначение
Рисунок 1 - Функциональная схема таймера КР1006ВИ1
и условное его обозначение
Напряжение от делителя U>1>=1/3Uг подается на неинвертирующий вход компаратора запуска (К1), а напряжение U>2>=2/3Uп - на инвертирующий вход компаратора сброса (К2). В процессе работы компараторы выполняют функцию управления таймером, в частности, триггером.
Триггер формирует импульсы прямоугольной формы и, в свою очередь, управляет работой разрядного транзистора Т11.
Компаратор К1 в процессе управления триггером. а следовательно, и таймером, обладает приоритетом перед компаратором К2. Это означает, что в случае, когда на вход компаратора К1 подано напряжение запуска ( Uвх>1><U>1>), то независимо от уровня напряжения на входе компаратора К2 (Uвх>2><U>2>,Uвх>2>>U>2>) триггер устанавливается в состояние, соответствующее состоянию запуска таймера.
Транзистор Т10 служит для блокировки работы таймера. На эмиттер этого транзистора подается напряжение Uоп, формируемое внутренними элементами таймера.
Рассмотрим назначение выводов таймера.
Вывод 1 - общий ( земля )
Вывод 8 - на этот вывод подается напряжение питания ( 4,5-16 Вольт). Приращение потребляемого таймером тока на 1 Вольт изменения источника питания составляет 0,007 Ампер.
Вывод 2 - через него осуществляется запуск таймера, эту цепь обычно называют триггерным входом. По отношению к выходу этот вход является инвертирующим. В астабильном режиме он соединяется с выводом 6.
Вывод 3 - он является низкоомным выходом таймера.
Вывод 4 - через него осуществляется сброс таймера, т.е. он служит для установления на его выходе низкого напряжения независимо от напряжения на выводах 2 и 6. Если напряжение на этом выводе U>4><0.4 Вольт, то напряжение на выходе таймера будет составлять 0,1 - 0,2 Вольта. При напряжении U4>1 Вольт цепь сброса таймера выключена и не влияет на его работу. Если в процессе работы таймера нет необходимости его прерывать, то вывод 4 соединяют с выводом 8, как показано на рисунке 1.б.
Вывод 5 - через него осуществляется доступ к входам внутренних компараторов, на которые поданы пороговые напряжения. Чтобы избежать влияния внешних помех и пульсаций напряжения питания на точность работы таймера, рекомендуется шунтировать вывод 5 конденсатором, емкостью около 0,01 микроФарад.
Вывод 6 - при высоком напряжении на выводе 2 ( > 1/3 Uп ) состоянием выхода таймера можно управлять с помощью компаратора К2 по этому выводу, называемому пороговым входом таймера. В моностабильном режиме этот вывод обычно соединяют с выводом 7.
Вывод 7 - он является вспомогательным высокоомным выходом, который представляет собой открытый коллектор транзистора Т11. Этот вывод обычно используется для организации цепей обратной связи с выхода на входы (выводы 2 и 6 ) таймера.
2.4 Внутренняя структура таймера
Рассмотрим принципиальную схему таймера КР1006 ВИ1, показанную на рисунке 2.
Резисторная цепочка делителя, которая определяет пороговые значения напряжения, включает в себя пятикилоомные резисторы R>7>,R>8> и R>9> и транзисторы смещения TV9 и TV15 верхнего К2 и нижнего К1 компараторов соответственно. Транзисторы TV1 - TV8 составляют верхний компаратор. Транзисторы TV1 - TV4 используются как основная нагрузка для увеличения коэффициента усиления компаратора. Входные дифференциальные каскады собраны на транзисторах по схеме Дарлингтона, используемые в разработке компаратора, обеспечивают высокое входное сопротивление и низкий входной ток, что допускает широкий диапазон значений внешнего времязадающего резистора, используемого для конкретного применения.
Два выхода компараторов, взятые от коллекторов транзисторов TV2,TV12 и TV13, питают управляющий триггер, который состоит из TV17 и TV18. Транзисторы TV5 и TV19 являются транзисторами смещения для нижнего компаратора и триггера.
Выходной каскад таймера - это универсальная двухтактная схема, состоящая из транзисторов TV20 - TV23. Она может быть источником или приемником тока в 200 миллиАмпер при напряжении питания 15 Вольт и может управлять входами ТТЛ - кристаллов с питанием 5 Вольт.
Работу схемы можно объяснить следующим образом. Запускающий входной импульс, величина которого ниже, чем 1/3 Uп, поступивший на базу транзистора TV12 ( вывод 2 ), отпирает транзисторы TV12 и TV13 и вызывает положительный перепад на выходе компаратора на резисторе R>6>. Это является причиной отпирания транзистора TV16, вызывающего снижения потенциала на его коллекторе, что устанавливает фиксацию триггера путем запирания транзистора TV17 и открывания TV18, которые затем ведут к понижению потенциала коллектора транзистора TV18 и, следовательно, к понижению напряжения на выходе триггера. Для такого состояния триггера транзистор TV20 и разряжающий транзистор TV11 будут выключены и выход (вывод 3) будет иметь высокий потенциал. Это установленное состояние фиксации останется до тех пор, пока схема не будет вновь возвращена в исходное состояние.

Рисунок 2 - Принципиальная схема таймера КР1006ВИ1
Когда напряжение на выводе 6 достигнет верхнего порогового напряжения 2/3Uп, потенциал на выходе TV2 повышается и включается транзистор TV17. Транзистор TV17 снимает питание с базы TV18 и, следовательно, запирает его и происходит перебрасывание триггера. Альтернативный способ переброса триггера производится подачей низкого уровня напряжения на вход сброса (вывод4), который соединен с базой транзистора TV10. Это позволяет открыть TV10, который в свою очередь запирает транзистор TV18 путем устранения питания его базы и изменяет на обратное смещение диода Д>1>. Независимо от используемого метода вновь установленное состояние выключает транзистор TV18 и запирает TV20. При этом высоком выходе триггера разряжающий транзистор TV11 и выходной токоприемный транзистор TV23 оказываются открытыми, а выход находится в своем низком состоянии, которое определяется величиной напряжения коллектор - эмиттер в режиме насыщения транзистора TV23.
Таким образом, отметим особенности управления выходным напряжением таймера с помощью сигналов, подаваемых на входы компараторов К1 и К2:
1) Напряжение высокого уровня на выходе таймера устанавливается только в том случае, когда на вход К1 подается напряжение низкого уровня Uк>1><U>1> ( независимо от уровня напряжения на входе К2 ). После установки на выходе напряжения высокого уровня любое изменение Uк>1> не приводит к изменению состояния выходного каскада, если Uк>2><U>2>.
2) Напряжение низкого уровня на выходе таймера устанавливается только в том случае, когда на вход К2 подается напряжение высокого уровня Uк>2>>U>2>, а Uк>1>>U>1>. После этого любое изменение Uк>2> не приводит к изменению состояния выходного каскада, если Uк>1>>U>1>.
Так как резисторы R>1>=R>2>=R>3>=5кОм, пороговые напряжения связаны между собой соотношением U>1>=0.5U>2>.
Значения напряжений Uвх>1> и Uвх>2> на входах компараторов К1 и К2 в моменты запуска и сброса таймера должны удовлетворять условиям, приведенным в таблице 1, где U1 - напряжение срабатывания компаратора К1 ; U2 - напряжение срабатывания компаратора К2. В этой же таблице представлены уровни напряжения на выходе таймера и состояние транзистора Т11.
Таблица 1 - Режимы работы таймера

В процессе работы таймера напряжения на входах его компараторов могут принимать одновременно значения Uвх>1>>U>1> и Uвх>2><U>2>.
При таком сочетании напряжений сохраняется предыдущее состояние таймера, которое установилось или после его запуска, или его сброса.
Если в процессе работы таймера на вход блокировки подать напряжение низкого уровня (логический ноль), то таймер переходит в пассивный режим.
2.5 Работа таймера в моностабильном режиме
Рассмотрим работу таймера, включенного по схеме одновибратора, изображенного на рисунке 3 и на рисунке 4.

Рисунок 3 - Функциональная схема одновибратора

Рисунок 4 - Упрощенная Рисунок 5 - Временные диаграммы
схема одновибратора
В исходном состоянии триггер находится в режиме сброса, на его выходе поддерживается напряжение низкого уровня, разрядный транзистор открыт и, следовательно, конденсатор С разряжен.
При поступлении на вход таймера ( вывод2 ) запускающего импульса отрицательной полярности срабатывает компаратор К1 (когда Uзап < U>1>) и происходит запуск таймера.
В результате на выходе таймера (вывод 3) устанавливается напряжение высокого уровня (логическая единица) и разрядный транзистор VT11 закрывается. После этого начинается заряд конденсатора С током, протекающим от источника +Uп через резистор R. В момент когда возрастающее напряжение на конденсаторе становится равным пороговому напряжению U>2>, срабатывает компаратор К2 и происходит сброс таймера.
На выходе одновибратора устанавливается напряжение низкого уровня (логический ноль) и транзистор Т11 открывается. Конденсатор С быстро разряжается через транзистор Т11 и схема возвращается в исходное устойчивое состояние (в режим ожидания), ожидая прихода следующего запускающего импульса.
Таким образом, в процессе заряда времязадающего конденсатора С на выходе одновибратора формируется импульс длительностью
t=RCln[(Uп - Uост)/(Uп - U>2>)],
где Uост - остаточное напряжение на коллекторе насыщенного транзистора Т11. Временные диаграмы показаны на рисунке 5.
Время в течение которого на выходе таймера сохраняется высокий уровень напряжения, равного Uп, можно вывести относительно простым путем.
Общее выражение напряжения на конденсаторе С экспоненциально нарастающее от приблизительно нулевого потенциала до питающего напряжения Uп, имеет вид :
Uc(t) = U (1 - e
- t/ ),
),
где
 =
RC - постоянная времени цепи RC.
=
RC - постоянная времени цепи RC.
Так как хронирующий период ( т.е. заряд конденсатора ) заканчивается, когда напряжение на конденсаторе достигает значения U>2 >= 2/3Uп, уравнение для такого условия принимает вид.
Uc = 2/3Uп =
Uп(1 - e
- t/ )
;
)
;
Решив это уравнение для t, получим
t = 1,0986 RC,
или t = 1,1 RС.
Это уравнение является основным уравнением для хронирующего времени таймера КР1006ВИ1, работающего в качестве моностабильного таймера.
Отметим, что рекомендуемая ширина запускающего импульса должна удовлетворять условию
t>зап> < t/4.
При расчете RC - цепи одновибратора следует учитывать, что низкий уровень напряжения запуска не должен сохраняться дольше времени 1,1RC. Нарушение этого условия приводит к тому, что через время t>зап> таймер начнет генерировать импульсы произвольной формы.
Это объясняется тем, что компараторы таймера не равносильны по своему воздействию на RS - триггер. Компаратор К1, управляемый по выводу 2, обладает, как было сказано выше, приоритетом при установлении состояния триггера.
Если необходимо управлять одновибратором с помощью импульсов длительностью t>зап >> 1,1RC, то их следует подавать через дифференцирующую R>1>C>1> - цепь. Диод Д>1, показанный на рисунке 3,> ограничивает напряжение на выводе 2 на уровне Uп + Uд.
Если на вывод 5 подать регулирующее напряжение, то схема становится ждущим мультивибратором с регулируемой длительностью импульса.
Зависимость длительности импульса от регулирующего напряжения Uрег имеет вид
t = RC ln[(Uп - Uост)/(Uп - Uрег)] ;
2.6 Работа таймера в астабильном режиме
Рассмотрим принцип работы таймера в режиме мультивибратора, схема которого показана на рисунке 6.

Рисунок 6 - Схема мультивибратора
Формирование на выходе схемы последовательности импульсов происходит в результате заряда и разряда времязадающего конденсатора С. Переключение цепи RC осуществляют компараторы К1 и К2. Таймер всегда находится в рабочем режиме.
При подключении схемы к источнику питания конденсатор С начинает заряжаться по цепи R>1>C>1> от установившегося значения нижнего порогового уровня напряжения U>1> до верхнего порогового уровня напряжения U>2>, стремясь в пределе зарядиться до максимального значения выходного напряжения Umax (равного Uп), а разряжается от уровня напряжения U>2> до уровня напряжения U>1>, стремясь разрядиться до минимального значения выходного напряжения Umin.
Другими словами, когда напряжение на входе "ПОРОГ" (вывод 6) превысит две трети напряжения питания, состояние на входе верхнего компаратора К2 изменится и на выходе триггера появится напряжение высокого уровня (логическая единица), которое откроет транзистор VT11. Из-за наличия инвертирующего усилителя на "ВЫХОДЕ" (вывод 3) формируется напряжение логического нуля.

Рисунок 7 - Временные диаграммы
Теперь конденсатор С будет разряжаться током, который будет протекать через резистор R2 и транзистор VT11. Через некоторое время напряжение на входе "ЗАПУСК" (вывод 2) уменьшится до одной трети напряжения источника питания и компаратор К1 изменит свое состояние, возвратив триггер в исходное состояние (единичное). На выходе Q появится напряжение низкого уровня, транзистор VT11 откроется и на выходе таймера (вывод3) появится напряжение высокого уровня (логическая единица). Таким образом, весь цикл работы таймера повторяется непрерывно.
Длительность импульсов, формируемых при заряде (tз) и разряде (tр) конденсатора определяются выражениями :
tз=(R>1>+R>2>)C ln[( Umax - U>1> )/( Umax - U>2> )] ;
tp=R>2>C ln[( U>2> - Umin )/( U>1> - Umin )].
Выражения для tз и tp можно получить следующим образом.
Напряжение на емкости возрастает экспоненциально от 1/3Uп до 2/3Uп и определяется уравнением
Uc(t)=1/3Uп +
2/3Uп(1 - e
- tз/ ),
),
где
 =(R>1>+R>2>)C.
=(R>1>+R>2>)C.
Время заряда tз можно найти отсюда заменив Uc=2/3Uп. Тогда
Uc=2/3Uп=1/3Uп+2/3Uп(1 - e-t/((R1+R2)C)).
Отсюда tз=0,693(R>1>+R>2>)C = 0,7 (R>1>+R>2>)C.
Также напряжение на емкости, затухающее экспоненциально от 2/3Uп до нуля, определяется по формуле
Uc=2/3Uп e- tp/t,
где t=R>2>C.
Подставив вместо Uc=1/3Uп получим
Uc=1/3Uп=2/3Uп e - tp/R2C.
Таким образом, будем иметь
tp=0,693 R>2>C = 0,7 R>2>C.
Тогда период колебаний мультивибратора будет равен
T=tз+tр=0,7(2R>2>C+R>1>C).
Отсюда легко определить частоту автоколебаний таймера в этом режиме, а также скважность и коэффициент формы (Кф = tвкл/tвыкл ).
На рисунке 7 показана временная диаграмма работы мультивибратора. После включения питания Uп конденсатор С заряжается от 0 до 2/3Uп за время t>0>=1,1(R>1>+R>2>)C. Напряжение на выходе таймера в течение этого времени равно Uп. В момент t>0>, когда напряжение на С достигнет величины 2/3Uп, потенциал выводов 3 и 7 падает до нуля и конденсатор С начинает разряжаться от 2/3 до 1/3Uп. Время t>0> определяет продолжительность выхода таймера на периодический рабочий режим работы, после чего формируются одинаковые повторяющиеся сигналы.
Период автоколебаний можно регулировать изменяя пороговые напряжения U>1> и U>2>. Для этого можно выводами 5 и 8 или 5 и 1 таймера необходимо включить регулировочный резистор. При этом для обеспечения симметрии генерируемых мультивибратором импульсов должно быть выполнено условие
(Umax - U>1>)/(Umax - U>2>)=(U>2> - Umin)/(U>1> - Umin) ;
Если емкость конденсатора С изменять от 1000 пФ до 10 мкФ, сопротивления резисторов (R>1>+R>2>) от 1 до 1000кОм, длительность импульсов tз и tp будет изменяться от долей микросекунд до единиц секунд, а частота генерируемых колебаний соответственно от единиц МГц до долей Гц.
3 Описание лабораторной установки
На рисунке 8 показана передняя панель лабораторного макета и показано условное изображение таймера КР 1006ВИ1 со всеми выводами, набор резисторов R1 - R6 и емкостей С1 - С3, которые являются времязадающими элементами, а также светодиод на выходе таймера.

Рисунок 8 - Передняя панель лабораторного макета
Номиналы резисторов и емкостей :
R1=680кОм; R2=68кОм; R3=6,8кОм; R4=2кОм; R5=10кОм; R6=47кОм;
С1=1мкФ; С2=0,25мкФ; С3=0,15мкФ; Сш=0,01мкФ.
Светодиод АЛ307Б предназначен для индикации выхода таймера. В корпусе макета имеется встроенный генератор прямоугольных импульсов.
4 Программа работы
4.1 По указанному варианту рассчитать параметры схемы одновибратора и мультивибратора и исследовать их.
4.2 Снять осцилограммы напряжений.
4.3 Построить номограмму для инженерного расчета указанных схем и проверить ее.
4.4 Определить погрешность, которую дает таймер, рассчитанный по номограмме.
4.5 Ознакомиться с основными параметрами таймера, приведеннными в приложении В.
5 Содержание отчета
Отчет должен содержать
5.1 Расчеты схемы таймера в моностабильном и астабильном режимах работы.
5.2 Схемы одновибратора и мультивибратора.
5.3 Временные диаграммы.
5.4 Составленную собственную номограмму.
5.5Значения коэффициента форма и коэффициента заполнения (скважности) импульсов.
5.6 Полные выводы основных формул для таймера.
6 Контрольные вопросы
6.1 Показать на принципиальной схеме таймера компараторы напряжения, тригггерное устройство, делители напряжения, инвертор, разрядный ключ.
6.2 Как получить различные скважности импульсных сигналов на выходе таймера для обоих режимов его работы?
6.3 Как сократить время работы выхода таймера на рабочий режим в астабильной схеме?
6.4 Какими способами можно уменьшить погрешность таймера?
6.5 Доказать справедливость формул
t=1,1RC (одновибратор )
T=0,7R>2>C (мультивибратор)
6.6 На принципиальной схеме покажите опорное напряжение, поступающее на транзистор сброса.
6.7 Что нужно сделать, чтобы увеличить или уменьшить амплитуду выходного напряжения, при Uп=const?
Список литературы
1. Коломбет Е.А. Таймеры. - М.:Радио и связь, 1983.
2. Горошков Б.И. Элементы радиоэлектронных устройств. - М.:Радио и связь, 1988.
3. Токхейм Р. Основы цифровой техники. - М.: Мир, 1988.
4. Тули М. Справочное пособие по цифровой электронике. - М.: Энергоатомиздат, 1990.
Приложение В
Основные параметры мкросхемы КР1006ВИ1
1.Напряжение питания 4,5 - 16,5 В
2.Максимальный втекающий и
вытекающий ток нагрузки 100мА
3.Активный уровень блокированного входа <0,4 В
4.Потребляемый ток при Uп = 15В <15мА
5.Потребляемый ток при Uп=5 В 3 мА
6.Длительность положительного
и отрицательного фронтов выходного импульса <100мкс
7.Выходное сопротивление 10 Ом
8.Рассеиваемая мощность (Uп = 15 В) 600 мВт
9.Максимальное напряжение выводов 2,4,6,7 0 - 16,5В
10.Время задержки <200мкс
11.Температурная стабильность длительности 0,005%/с
12.Зависимость длительности от Uп 0,05%/В
13.Начальная погрешность 1%
14.Технология изготовления биполярная
Задание 1
Минимизировать следующие логические неполностью определенные функции и составить принципиальные схемы их реализации (в базисе И – НЕ).
|
Вариант |
Принимают значения, равные 1 на наборах |
Принимают значения, равные 0 на наборах |
|
3 |
15, 19, 23, 31 |
0, 11, 22, 27 |
|
7 |
6, 12, 15, 30 |
3, 14, 19, 31 |
Вариант 3
|
0 |
* |
* |
* |
* |
* |
* |
* |
|
* |
* |
* |
* |
* |
* |
* |
* |
|
* |
* |
1 |
0 |
0 |
1 |
* |
* |
|
* |
* |
* |
* |
1 |
1 |
0 |
* |
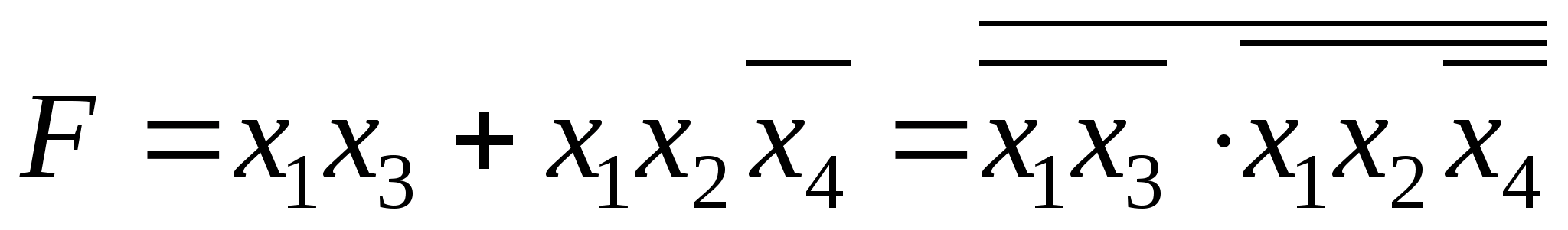
Вариант 7
|
* |
* |
* |
* |
* |
* |
* |
* |
|
* |
1 |
* |
* |
* |
* |
* |
* |
|
* |
0 |
1 |
* |
* |
0 |
1 |
* |
|
* |
1 |
* |
0 |
0 |
* |
* |
* |
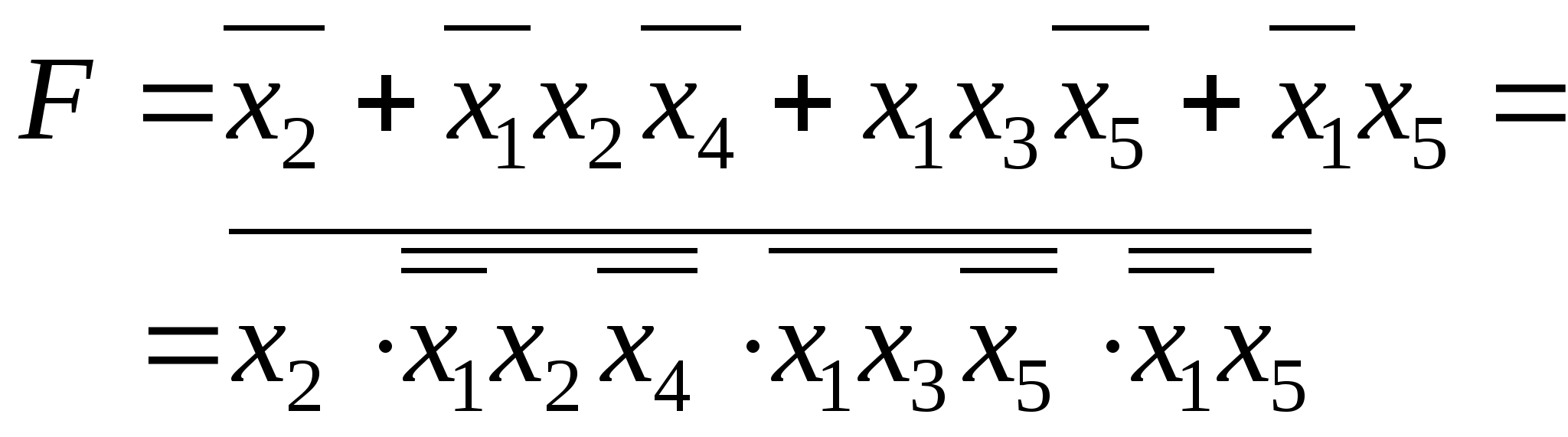
Задание 2
Минимизировать следующие полностью определенные логические функции, принимающие значения, равные 1 на указанных наборах и составить принципиальные схемы для их реализации (базис И – НЕ)
|
Вариант |
Принимают значения, равные 1 на наборах |
|
3 |
3, 6, 7, 14, 15, 19, 23, 30, 31 |
|
7 |
16, 18, 20, 21, 22, 26, 27, 28, 29 |
Вариант 3
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
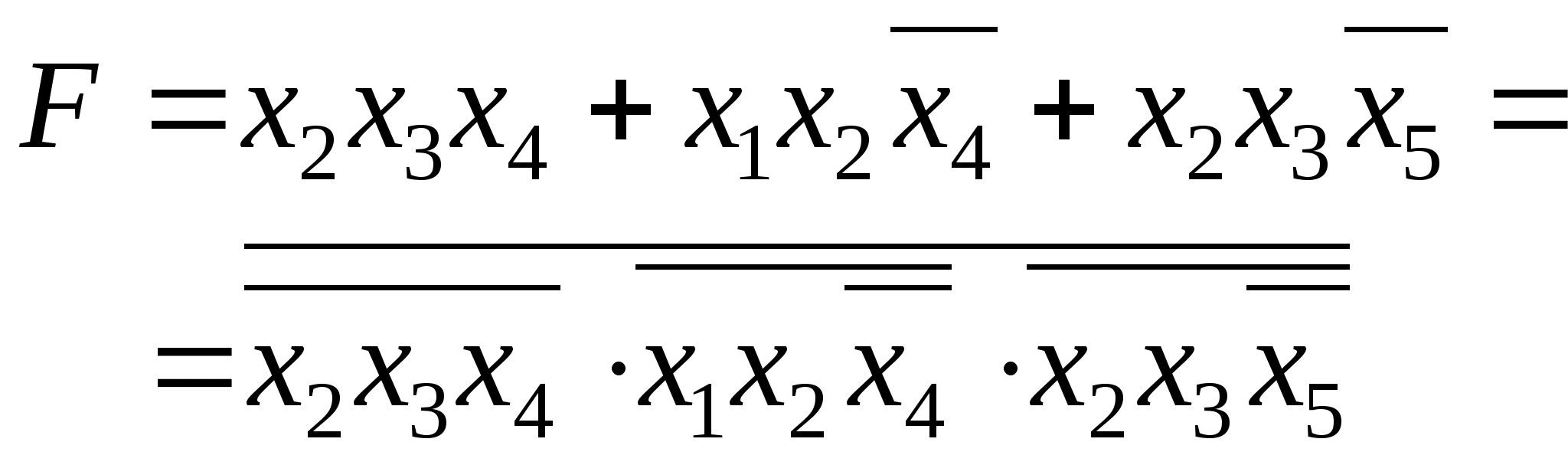
Вариант 7
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
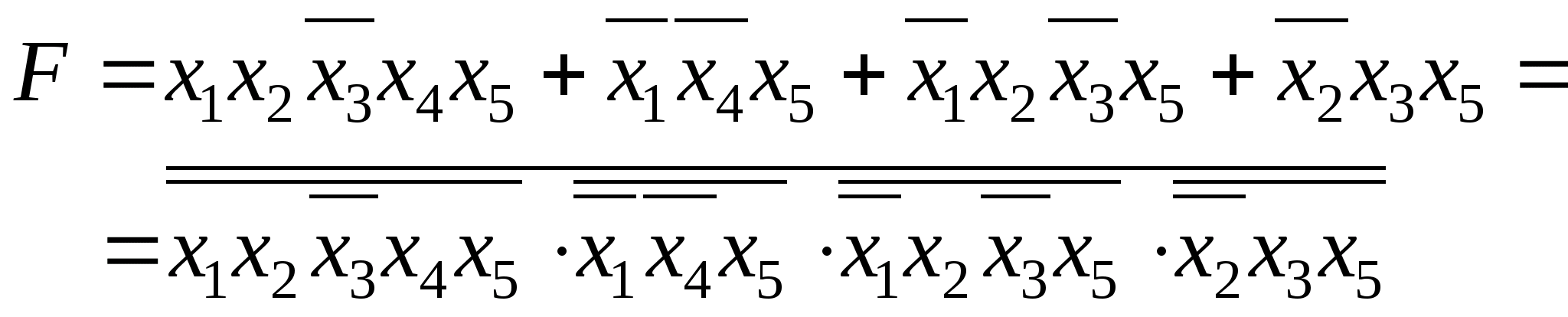
Задание 3
Минимизировать следующие полностью определенные логические функции, принимающие значения, равные 0 на указанных наборах и составить принципиальные схемы для их реализации (базис ИЛИ – НЕ).
|
Вариант |
Принимают значения, равные 0 на наборах |
|
3 |
3, 11, 15, 31 |
|
7 |
1, 9, 25, 27, 28, 29 |
Вариант 3
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
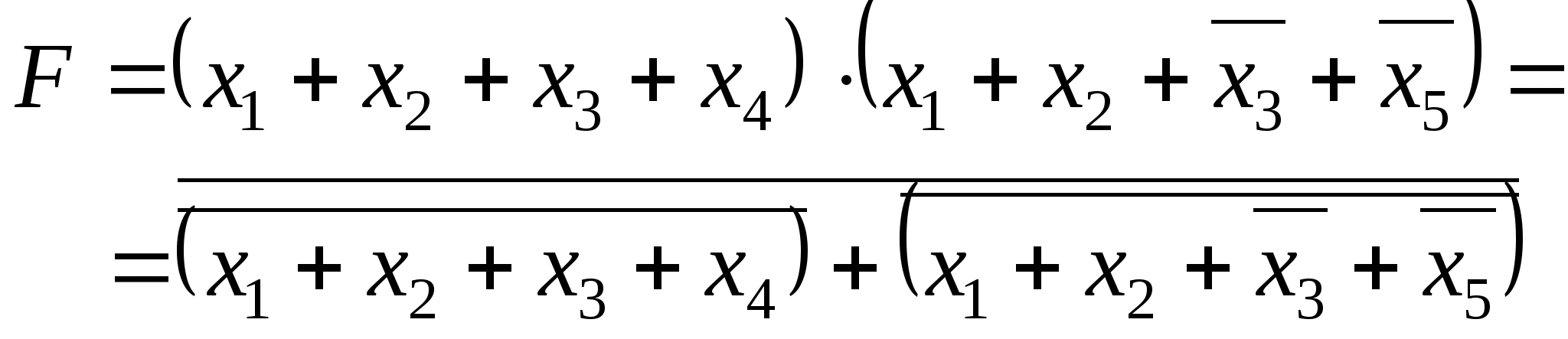
Вариант 7
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |


Задание 4
Минимизировать схему выбора чисел из 5-разрядного счетчика и составить принципиальную схему для реализации (на выходе схемы выбора должна появиться 1 при подаче на вход любого из выбираемых чисел). Базис ИЛИ – НЕ.
|
Вариант |
Условия выбора |
|
3 |
Всех чисел М>8 |
|
7 |
Всех чисел 20>М>27 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
2 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
3 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
4 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
5 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
6 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
7 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
8 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
9 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
10 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
11 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
12 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
13 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
14 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
15 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
16 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
17 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
18 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
19 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
20 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
21 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
22 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
23 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
24 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
25 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
26 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
27 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
28 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
29 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
30 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
31 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |

Вариант 7
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |


Задание 5
Минимизировать системы функций, описывающих преобразователи одного кода в другой.
|
Вариант |
Преобразователь кодов |
|
3 |
Двоичный код – код 4221 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
3 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
5 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
6 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
7 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
9 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
|
1 |
* |
* |
1 |
|
* |
* |
* |
* |
|
0 |
1 |
1 |
0 |
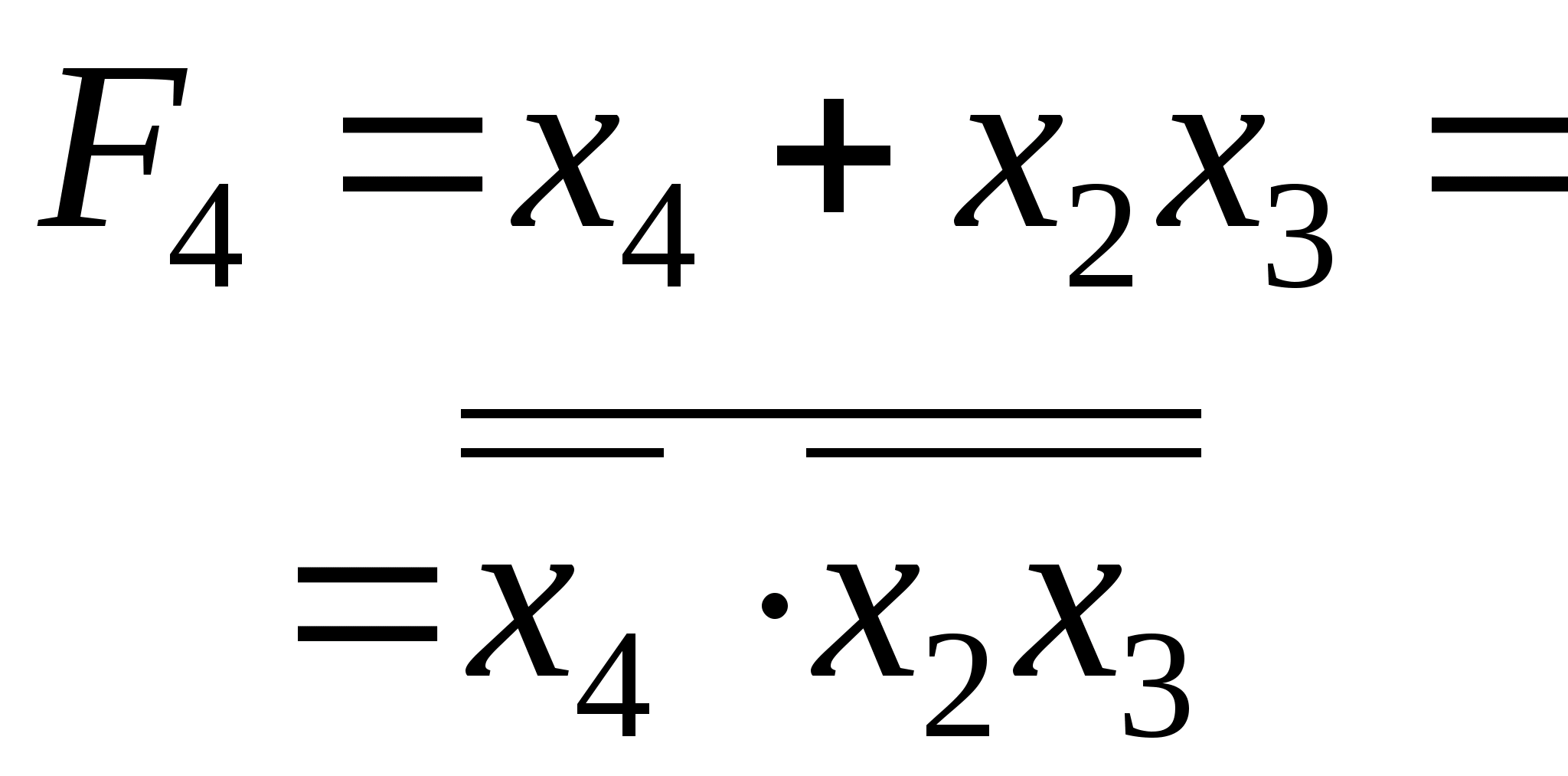
|
0 |
1 |
1 |
0 |
|
1 |
* |
* |
1 |
|
* |
* |
* |
* |
|
0 |
0 |
0 |
0 |
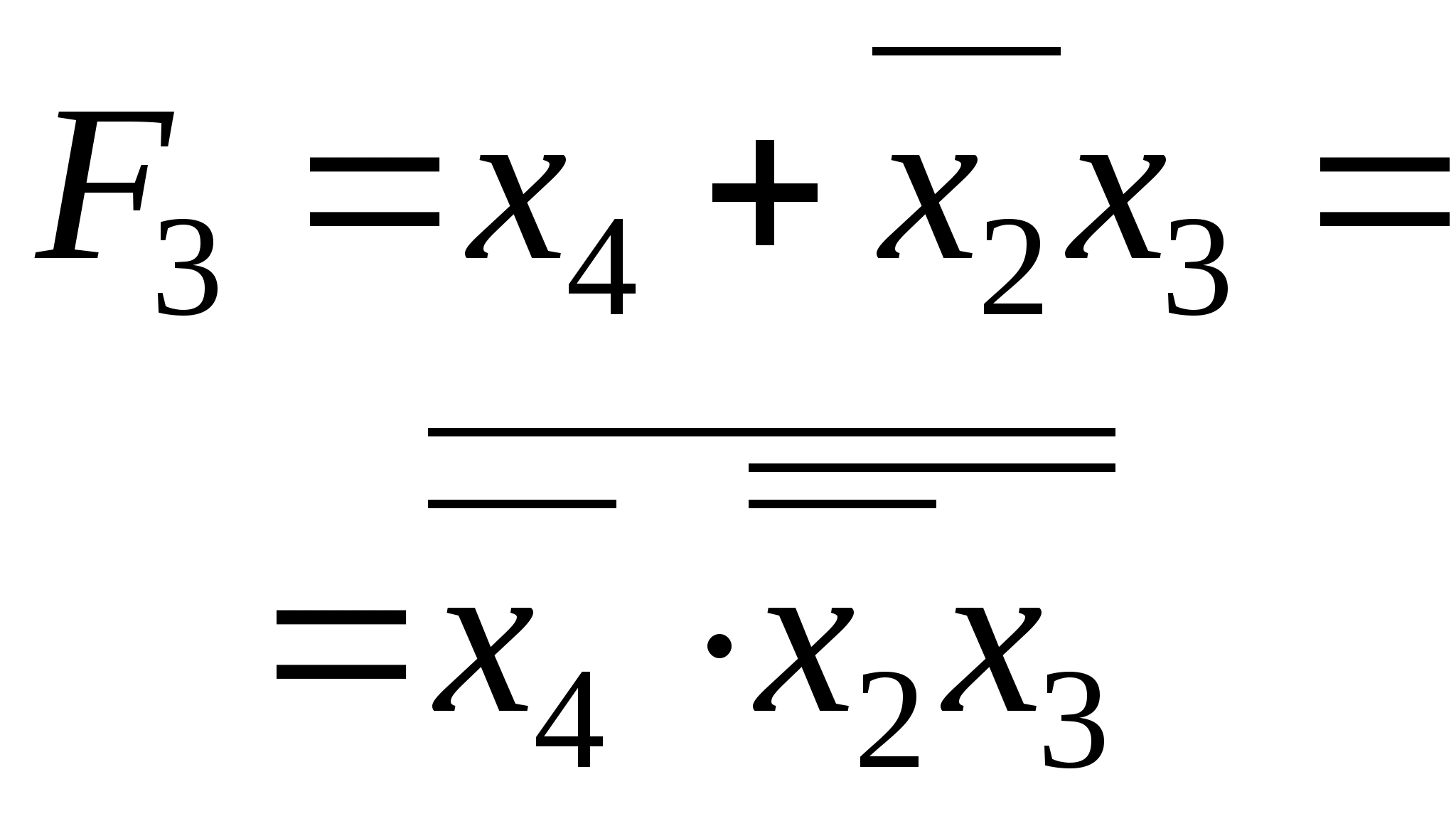
|
0 |
1 |
1 |
0 |
|
0 |
* |
* |
1 |
|
* |
* |
* |
* |
|
1 |
1 |
1 |
1 |
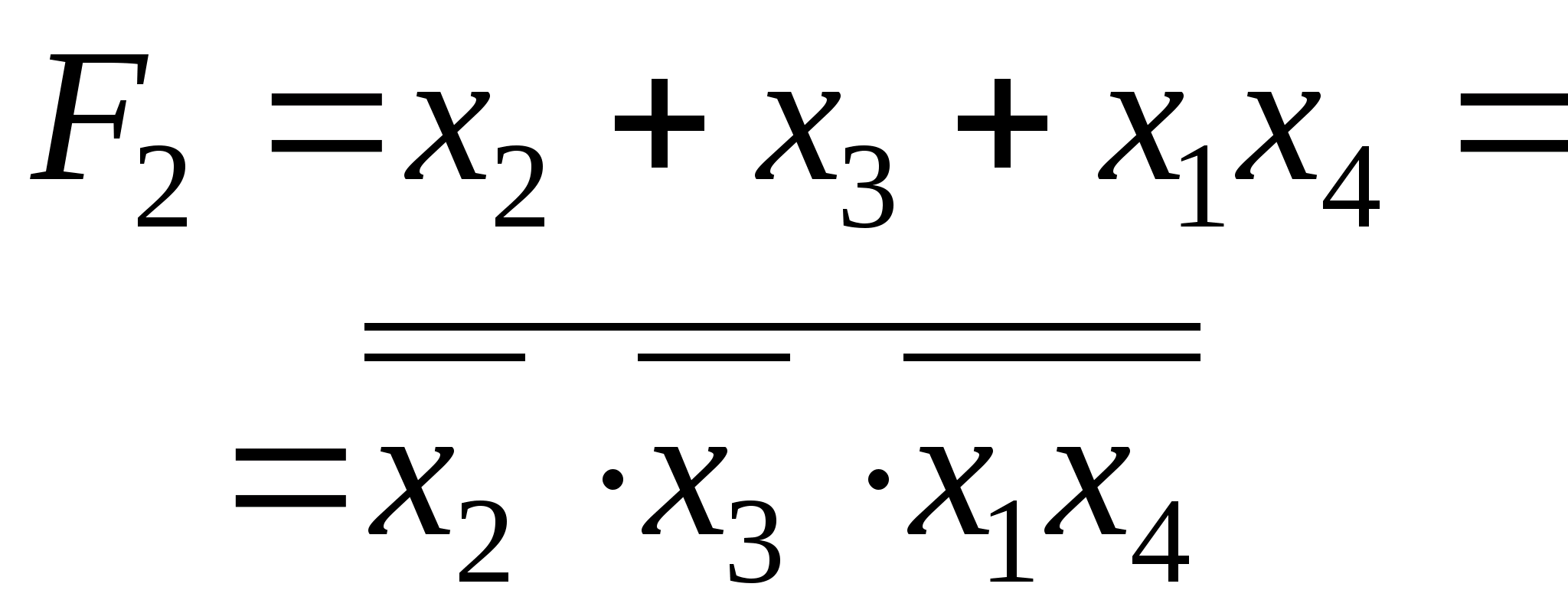
|
0 |
0 |
1 |
1 |
|
1 |
* |
* |
1 |
|
* |
* |
* |
* |
|
0 |
0 |
1 |
1 |
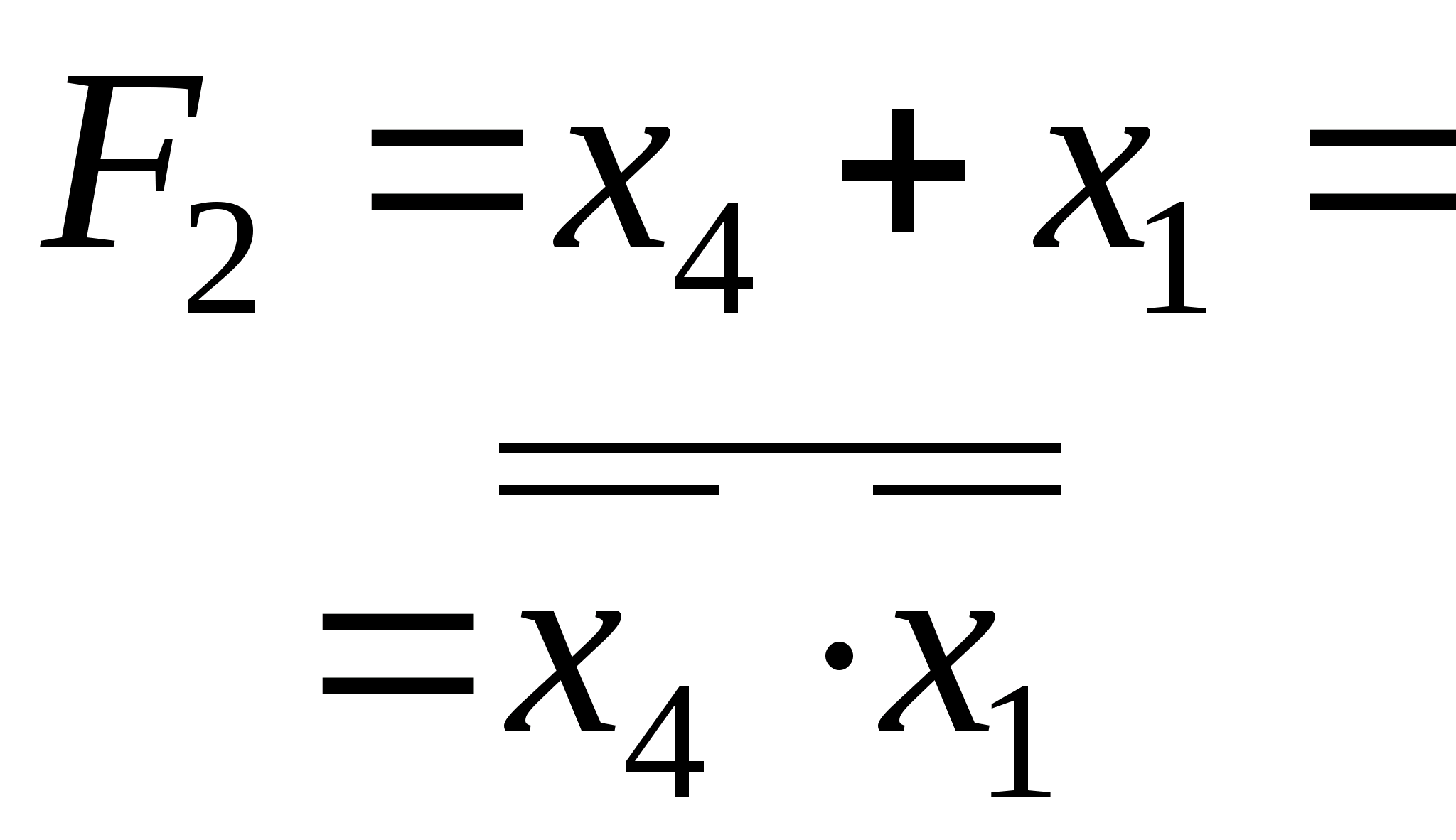
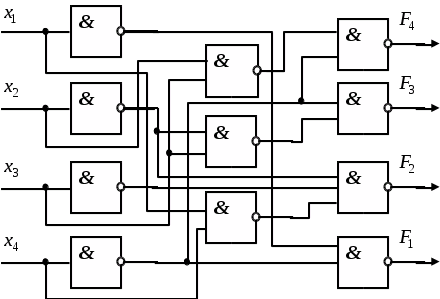
Задание 6
Построить схему порогового элемента на К входов (выходной сигнал равен 1, если суммарное число единиц на входах не меньше, чем значение порога Р) при разных весовых коэффициентах входов, указанных в задании.
|
Вариант |
К |
Р |
|
|
3 |
4 |
3 |
1 |
|
|
1 |
1 |
1 |
1 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
2 |
0 |
0 |
1 |
0 |
1 |
0 |
|
3 |
0 |
0 |
1 |
1 |
2 |
0 |
|
4 |
0 |
1 |
0 |
0 |
1 |
0 |
|
5 |
0 |
1 |
0 |
1 |
2 |
0 |
|
6 |
0 |
1 |
1 |
0 |
2 |
0 |
|
7 |
0 |
1 |
1 |
1 |
3 |
1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
0 |
|
9 |
1 |
0 |
0 |
1 |
2 |
0 |
|
10 |
1 |
0 |
1 |
0 |
2 |
0 |
|
11 |
1 |
0 |
1 |
1 |
3 |
1 |
|
12 |
1 |
1 |
0 |
0 |
2 |
0 |
|
13 |
1 |
1 |
0 |
1 |
3 |
1 |
|
14 |
1 |
1 |
1 |
0 |
3 |
1 |
|
15 |
1 |
1 |
1 |
1 |
4 |
1 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |

Задание 8
Построить мажоритарный элемент на 5 входов.
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
2 |
0 |
0 |
0 |
1 |
0 |
0 |
|
3 |
0 |
0 |
0 |
1 |
1 |
0 |
|
4 |
0 |
0 |
1 |
0 |
0 |
0 |
|
5 |
0 |
0 |
1 |
0 |
1 |
0 |
|
6 |
0 |
0 |
1 |
1 |
0 |
0 |
|
7 |
0 |
0 |
1 |
1 |
1 |
1 |
|
8 |
0 |
1 |
0 |
0 |
0 |
0 |
|
9 |
0 |
1 |
0 |
0 |
1 |
0 |
|
10 |
0 |
1 |
0 |
1 |
0 |
0 |
|
11 |
0 |
1 |
0 |
1 |
1 |
1 |
|
12 |
0 |
1 |
1 |
0 |
0 |
0 |
|
13 |
0 |
1 |
1 |
0 |
1 |
1 |
|
14 |
0 |
1 |
1 |
1 |
0 |
1 |
|
15 |
0 |
1 |
1 |
1 |
1 |
1 |
|
16 |
1 |
0 |
0 |
0 |
0 |
0 |
|
17 |
1 |
0 |
0 |
0 |
1 |
0 |
|
18 |
1 |
0 |
0 |
1 |
0 |
0 |
|
19 |
1 |
0 |
0 |
1 |
1 |
1 |
|
20 |
1 |
0 |
1 |
0 |
0 |
0 |
|
21 |
1 |
0 |
1 |
0 |
1 |
1 |
|
22 |
1 |
0 |
1 |
1 |
0 |
1 |
|
23 |
1 |
0 |
1 |
1 |
1 |
1 |
|
24 |
1 |
1 |
0 |
0 |
0 |
0 |
|
25 |
1 |
1 |
0 |
0 |
1 |
1 |
|
26 |
1 |
1 |
0 |
1 |
0 |
1 |
|
27 |
1 |
1 |
0 |
1 |
1 |
1 |
|
28 |
1 |
1 |
1 |
0 |
0 |
1 |
|
29 |
1 |
1 |
1 |
0 |
1 |
1 |
|
30 |
1 |
1 |
1 |
1 |
0 |
1 |
|
31 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |


Задание 1
Построить элементарный последовательный автомат в базисе И – НЕ.
|
|
|
|
|||
|
0 |
0 |
|
|||
|
0 |
1 |
|
|||
|
1 |
0 |
1 |
|||
|
1 |
1 |
0 |
|||
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
* |
|
0 |
0 |
1 |
1 |
* |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
* |
1 |
|
1 |
1 |
0 |
0 |
1 |
* |
|
1 |
1 |
1 |
0 |
1 |
0 |
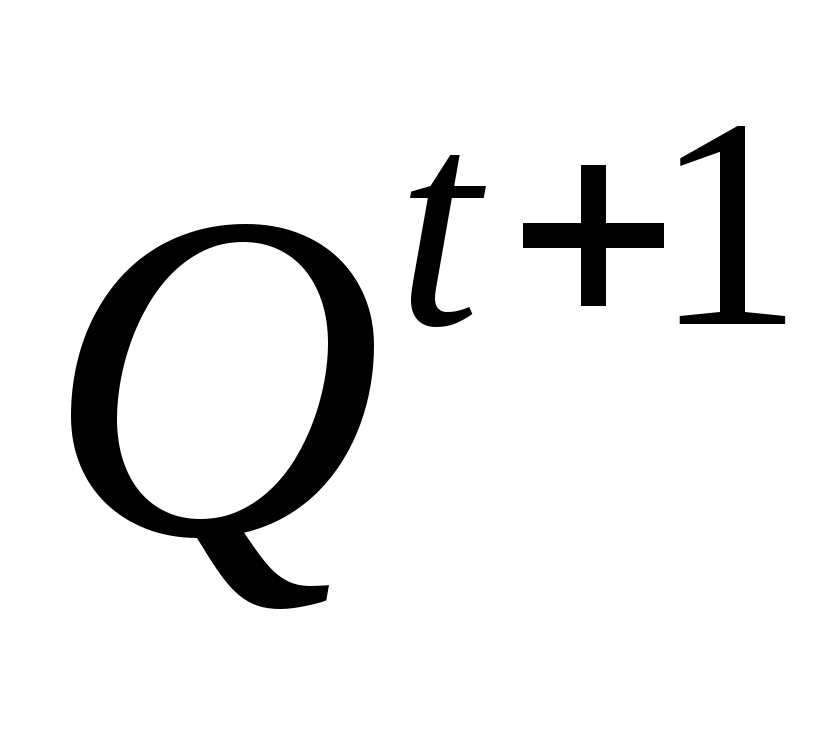 :
:
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |

Уравнение в базисе И – НЕ:
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |

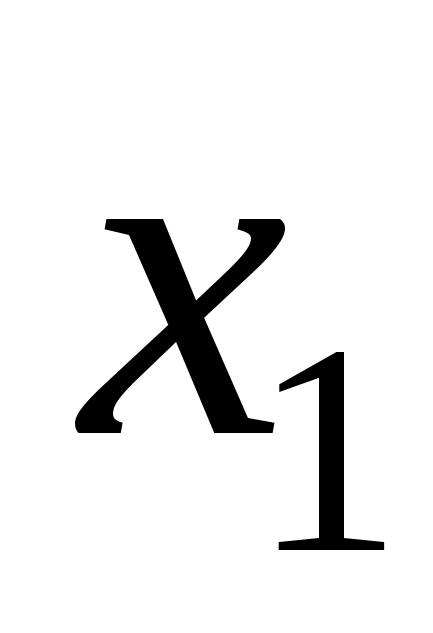

|
1 |
0 |
* |
* |
|
0 |
1 |
1 |
1 |
|
* |
1 |
1 |
1 |
|
1 |
* |
0 |
0 |


Задание 2
Построить элементарный последовательный автомат в базисе ИЛИ – НЕ.
|
|
|
|
|||
|
0 |
0 |
|
|||
|
0 |
1 |
1 |
|||
|
1 |
0 |
|
|||
|
1 |
1 |
|
|||
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
* |
|
1 |
0 |
0 |
0 |
* |
0 |
|
1 |
0 |
1 |
1 |
0 |
* |
|
1 |
1 |
0 |
0 |
* |
0 |
|
1 |
1 |
1 |
1 |
0 |
* |
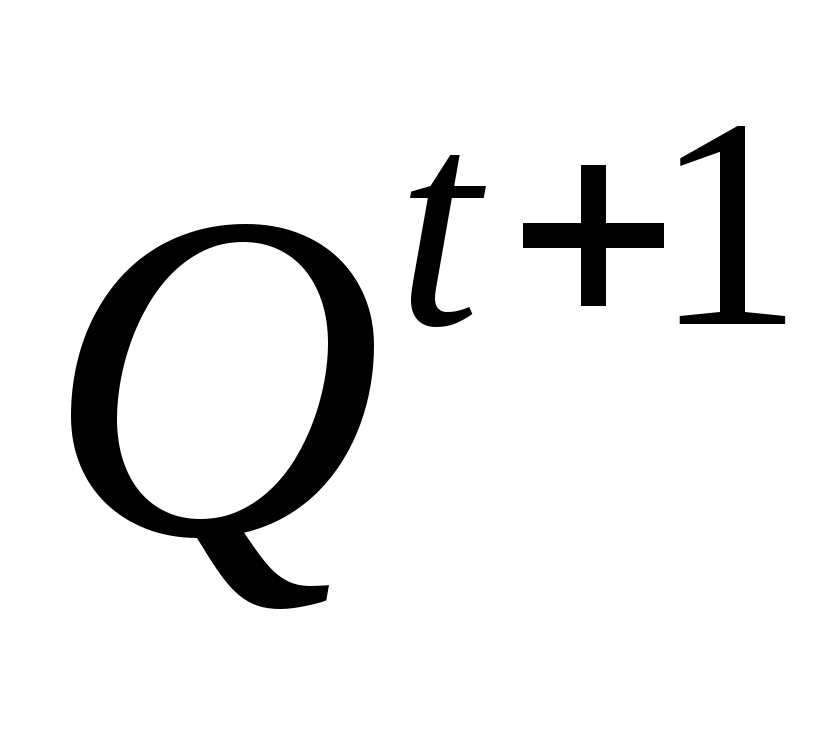 :
:
|
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |

Уравнение в базисе ИЛИ – НЕ:
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |

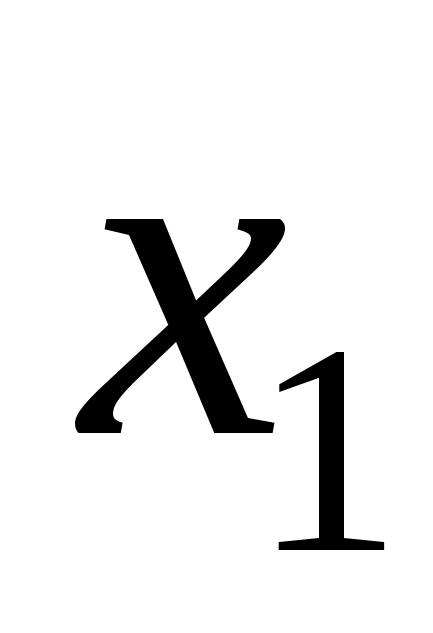

|
0 |
* |
0 |
1 |
|
0 |
* |
0 |
0 |
|
1 |
0 |
* |
0 |
|
1 |
0 |
* |
* |


Задание 3
Построить элементарный последовательный автомат с тремя входами.
|
|
|
|
|
|||
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
1 |
|
|||
|
0 |
1 |
0 |
1 |
|||
|
0 |
1 |
1 |
0 |
|||
|
1 |
0 |
0 |
1 |
|||
|
1 |
0 |
1 |
0 |
|||
|
1 |
1 |
0 |
|
|||
|
1 |
1 |
1 |
|
|||
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
* |
|
0 |
0 |
0 |
1 |
1 |
* |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
* |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
* |
|
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
* |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
* |
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
* |
|
1 |
1 |
0 |
1 |
1 |
* |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
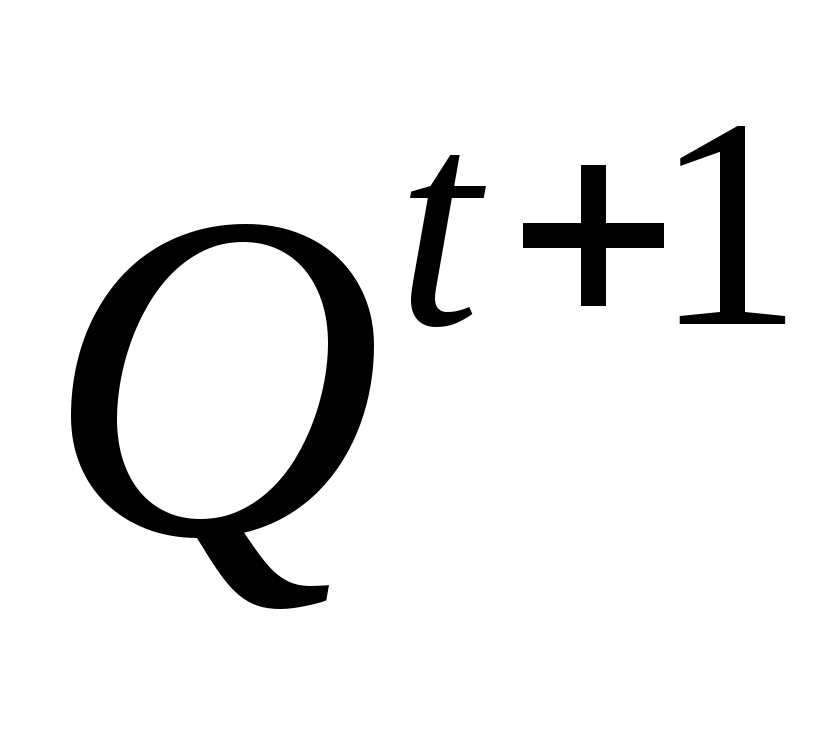 :
:
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |

|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
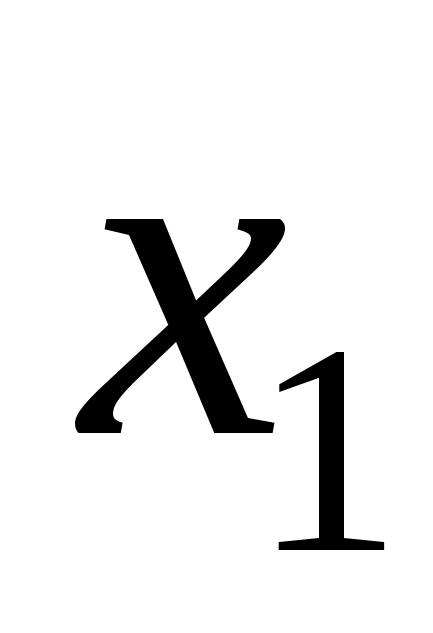
|
1 |
0 |
* |
* |
|
0 |
1 |
* |
* |
|
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |

|
* |
1 |
1 |
1 |
|
1 |
* |
1 |
1 |
|
* |
1 |
0 |
0 |
|
1 |
* |
0 |
0 |


Задание 1
Реализовать
заданную функцию на
 ,
,
 ,
,
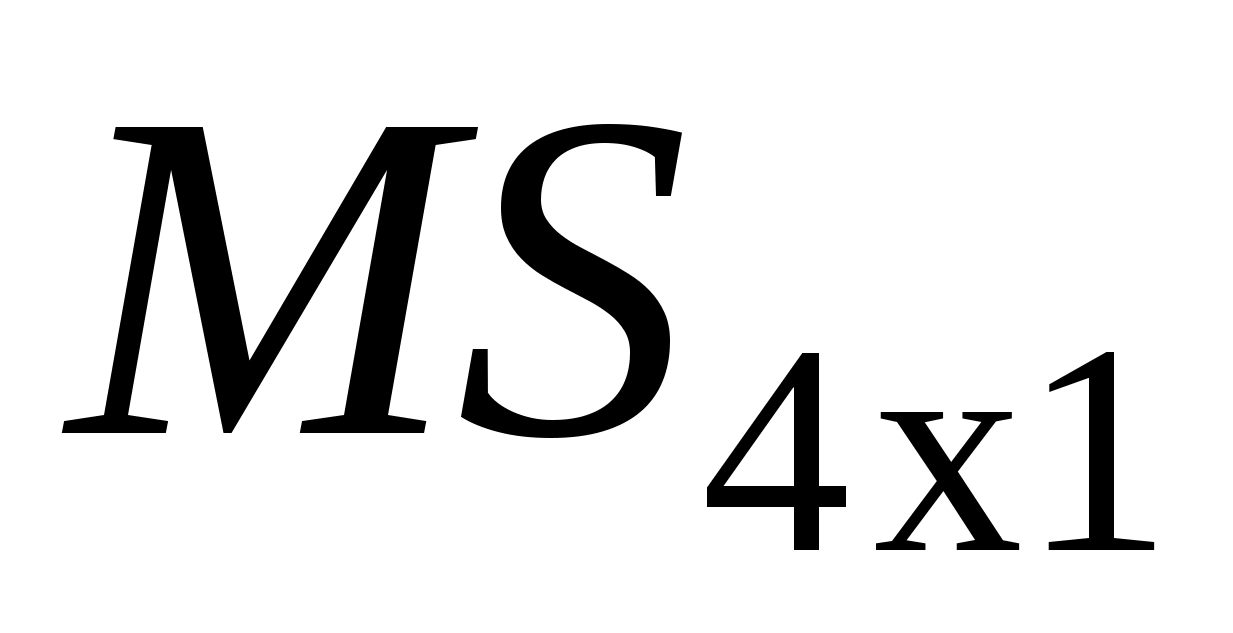 .
.
 .
.
Реализация
на
 .
.

|
|
|
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
|
|
0000 |
0001 |
|||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 ;
;
 ;
;
 .
.
Реализация
на
 .
.



Реализация
на
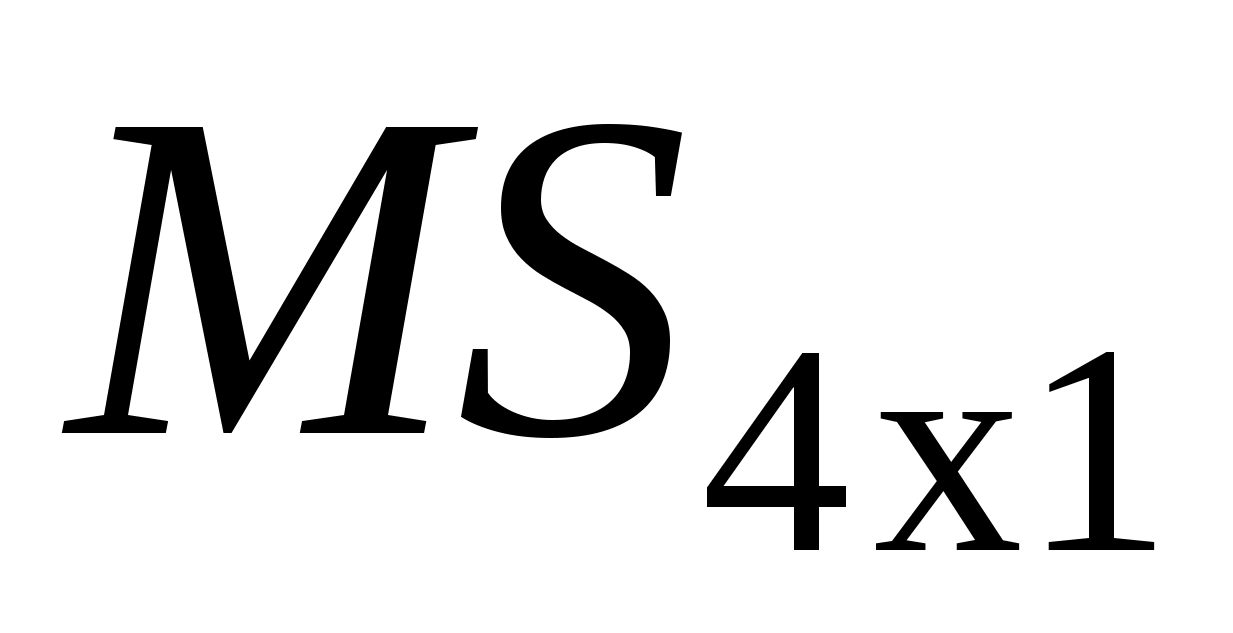 .
.





Задание 2
Реализовать
функцию
 на
на
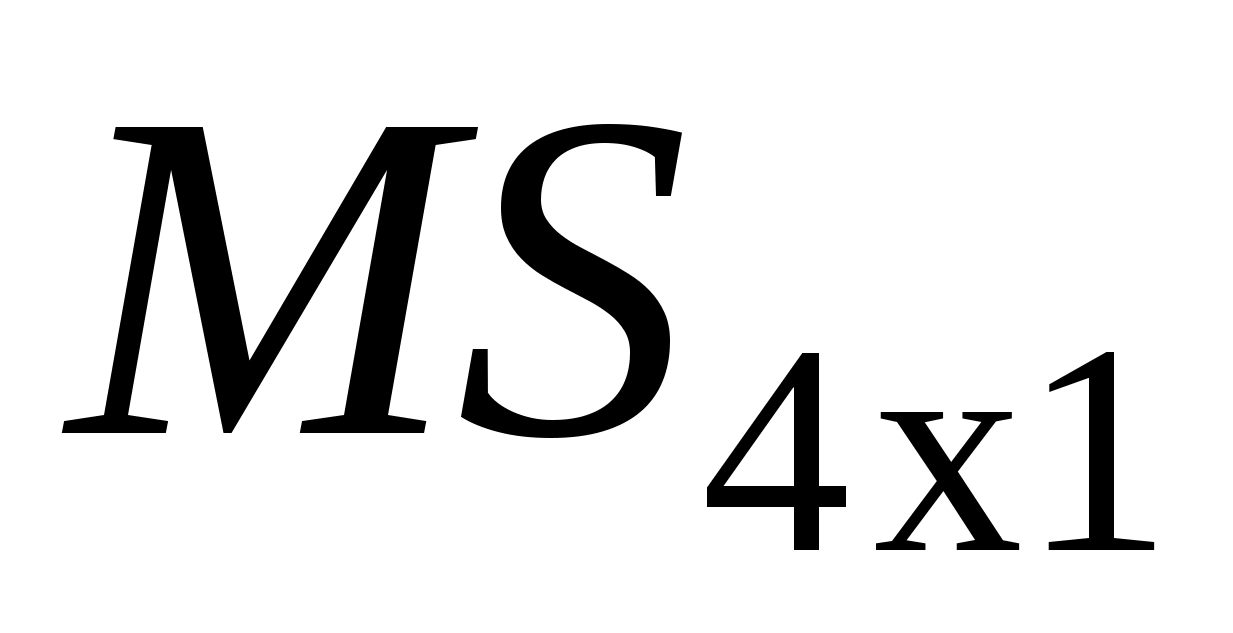 при:
при:



|
|
|
10 |
11 |
|
|
00 |
01 |
|||
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
|
|
|
|
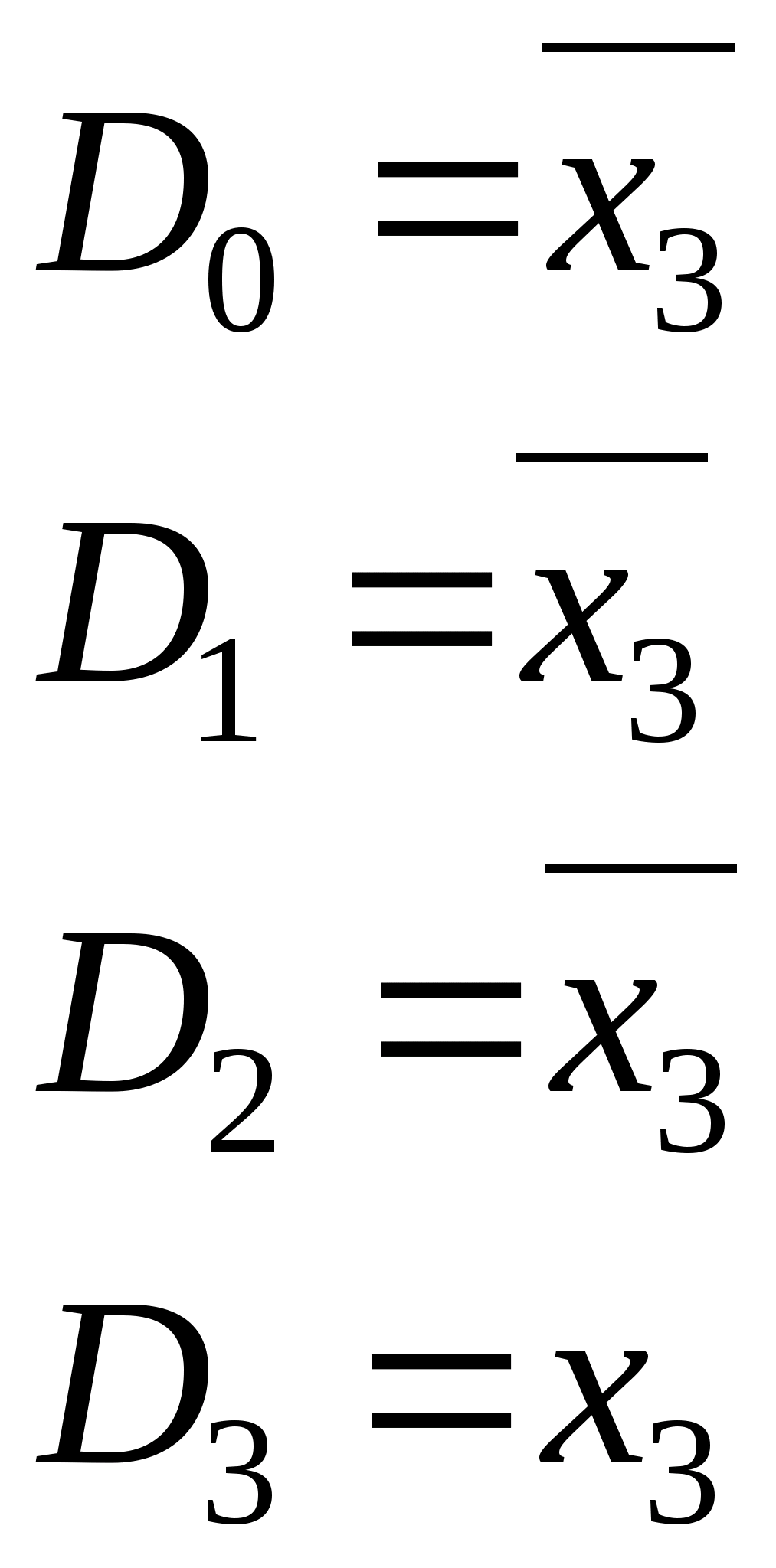

|
|
|
10 |
11 |
|
|
00 |
01 |
|||
|
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
|
|
|
|
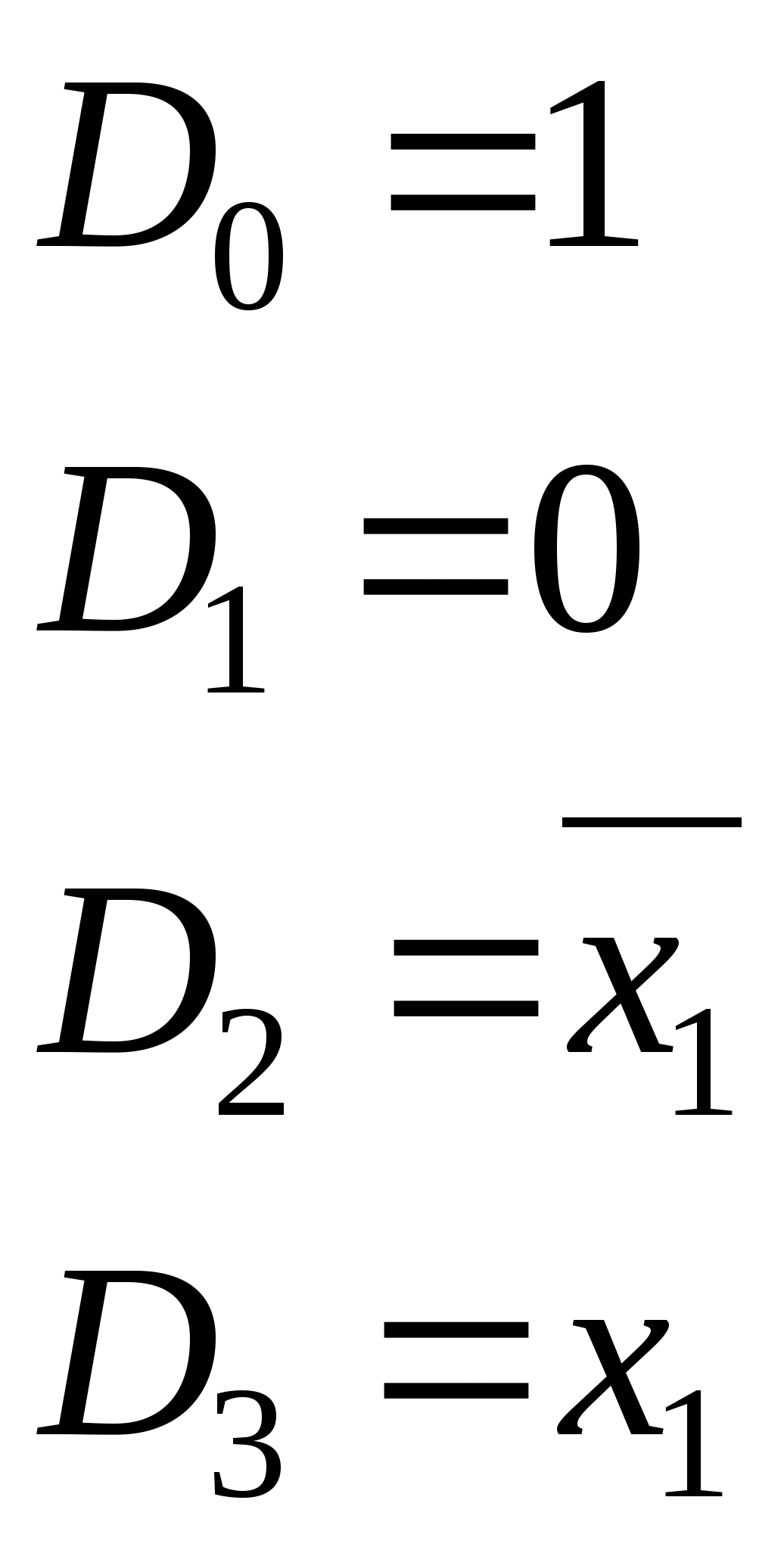

|
|
|
10 |
11 |
|
|
00 |
01 |
|||
|
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
|
|
|
|
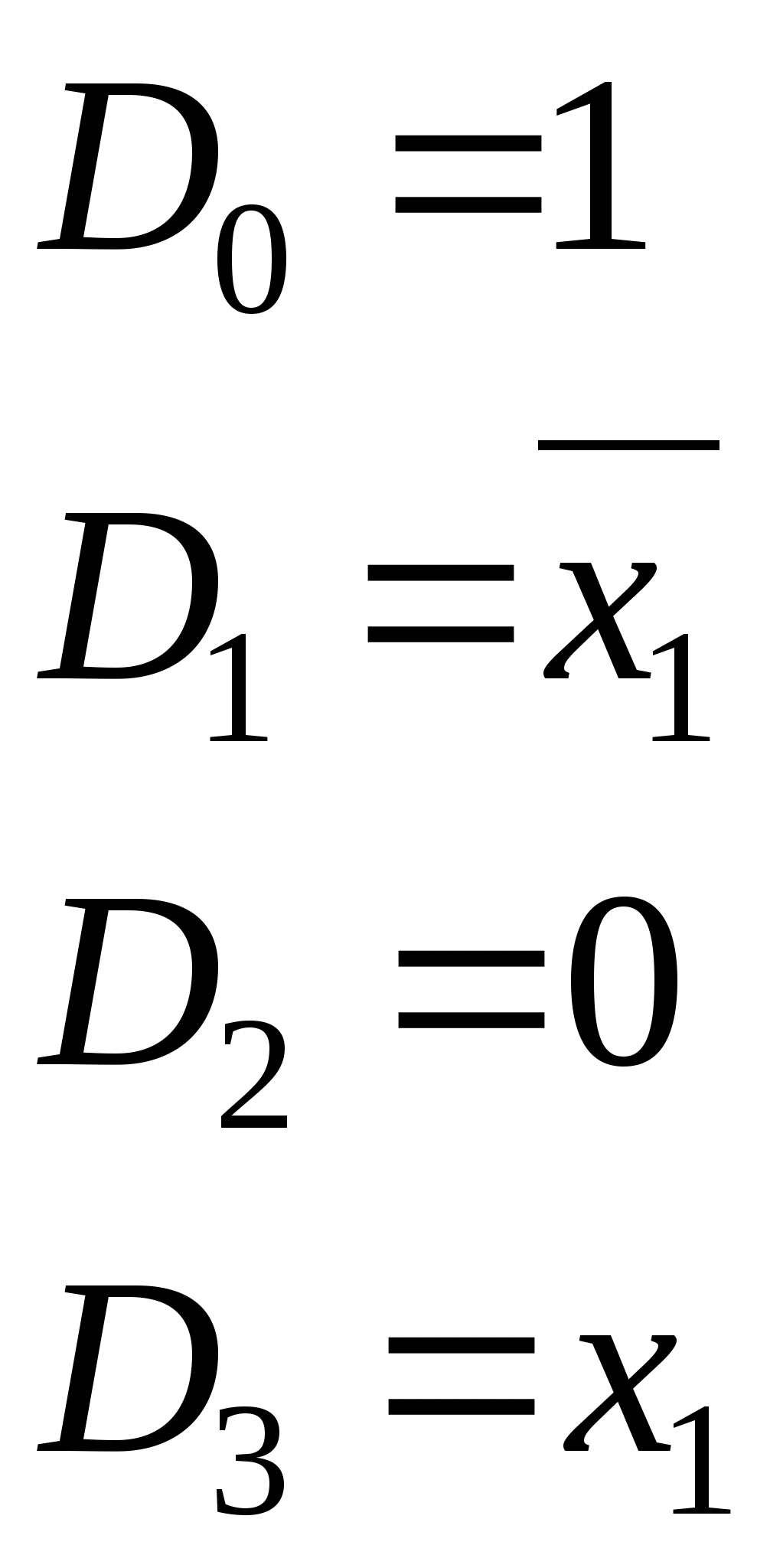

|
|
|
10 |
11 |
|
|
00 |
01 |
|||
|
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
|
|
|
|
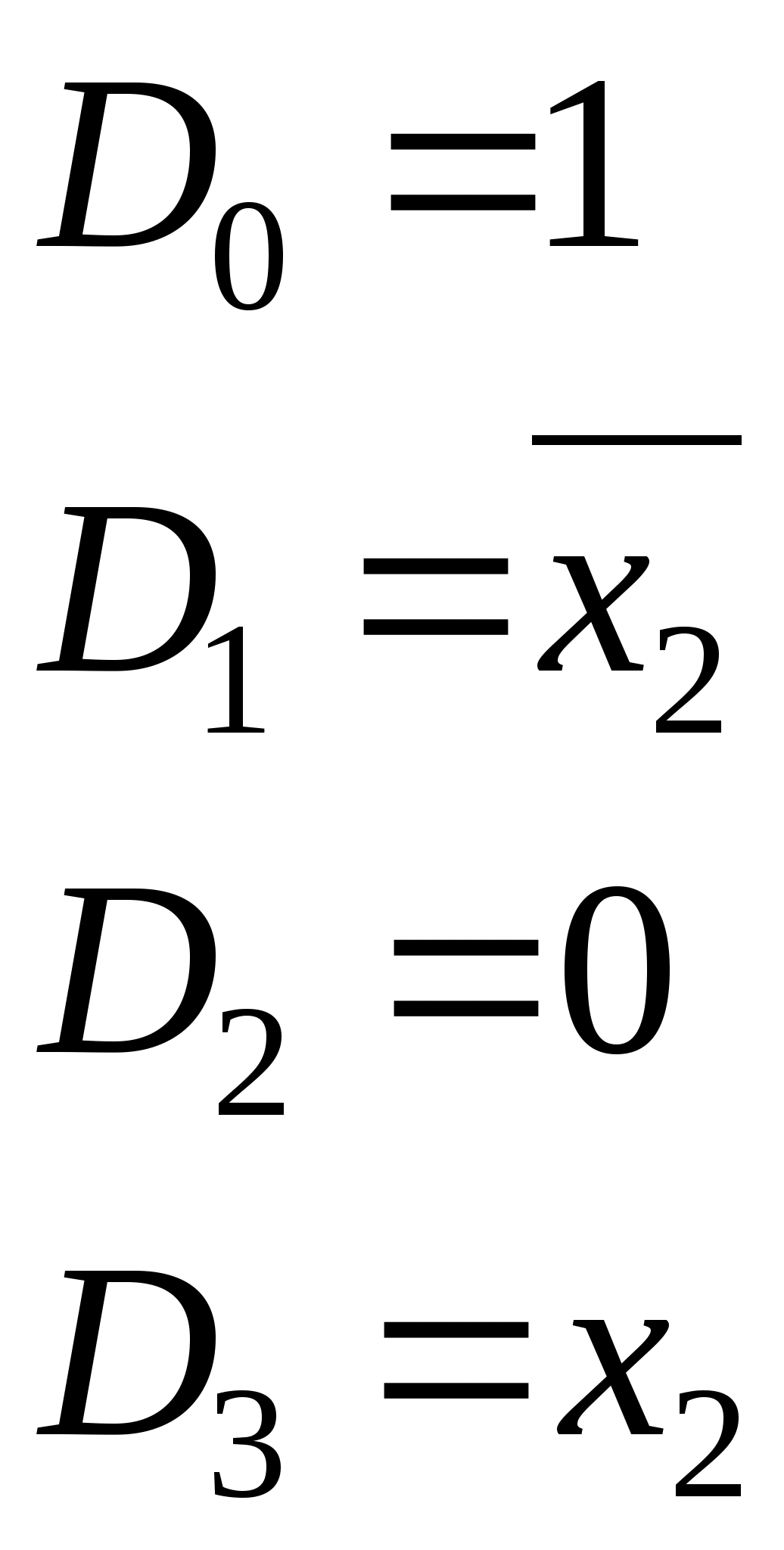
ХХ Основы булевой алгебры
Хх.1 Основные понятия и определения
Булева алгебра (БА) – раздел математической логики.
Основным понятием БА является высказывание (В). Под высказыванием понимают любое предложение, про которое можно однозначно сказать, истинно оно или ложно. Высказывания подразделяются на простые и сложные.
Под простым В понимают одно единственное предложение, про которое можно сказать истинно оно или ложно. Например: «Дважды два – пять», «Курица – не птица», «Путин – президент РФ».
Сложным В является предложение, состоящее из нескольких простых предложений (простых В), связанных между собой какими либо логическими связями. Под логическими связями понимаются грамматические союзы типа «НЕ», «И», «ИЛИ», «ЕСЛИ …, ТО …», и т.д.
Под булевой функцией (БФ) понимают сложное высказывание. Это такая функция, которая принимает лишь два значения (0 или 1). БФ всегда конечна и обозначается f, F. Простые высказывания, входящие в БФ, называются переменными или аргументами и обозначаются x, y, z, … В БА нет линейных коэффициентов, нет деления, корня, логарифма и т.д. В БА, как правило, используется двоичная арифметика, да и то не в полном объеме.
Есть два типа реализации БФ: положительная логика и отрицательная логика. В положительной логике 0 (ложь) соответствует низкому уровню сигнала, а 1 (истина) – высокому. Соответственно в отрицательной логике – наоборот.
БФ одной переменной называется симвилярной функцией. Существуют четыре симвилярные функции. Они приведены в таблице ХХ.1.
Таблица ХХ.1 Симвилярные БФ
N |
|
0 |
1 |
Обозначение |
Название |
|
0 |
|
0 |
0 |
0 |
Константа нуль |
|
1 |
|
0 |
1 |
|
Повторение |
|
2 |
|
1 |
0 |
|
Отрицание (инверсия) |
|
3 |
|
1 |
1 |
1 |
Константа единица |
Хх.2 БФ двух переменных
БФ двух переменных называются бинарными.
Существует шестнадцать бинарных функций. Они приведены в таблице хх.2.
Таблица хх.2 БФ двух переменных
|
x |
y |
F>0> |
F>1> |
F>2> |
F>3> |
F>4> |
F>5> |
F>6> |
F>7> |
F>8> |
F>9> |
F>10> |
F>11> |
F>12> |
F>13> |
F>14> |
F>15> |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
F>0>=0; F>1>= ;
;
F>2>= ; F>3>=
; F>3>=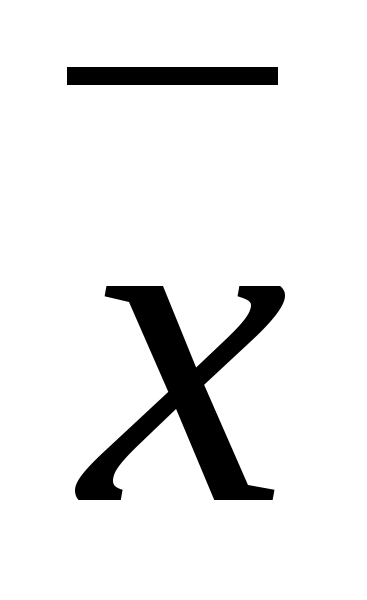 ;
;
F>4>= ; F>5>=
; F>5>=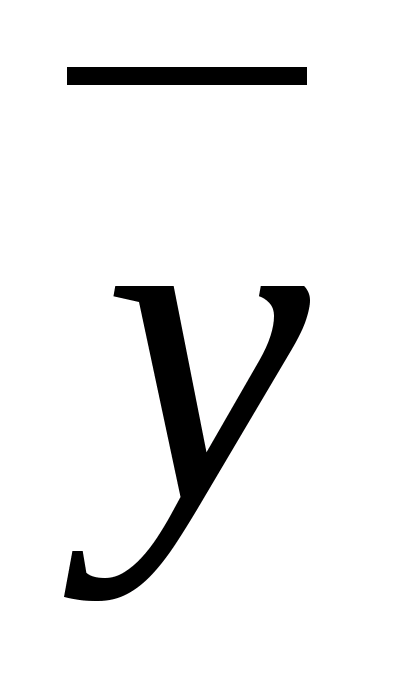 ;
;
F>6>= ; F>7>=
; F>7>= ;
;
F>8>= ; F>9>=
; F>9>= ;
;
F>10>= ; F>11>=
; F>11>= ;
;
F>12>= ; F>13>=
; F>13>= ;
;
F>14>= ; F>15>=1.
; F>15>=1.
Из всех возможных бинарных БФ выделяются нижеследующие основные.
Константа 0 – F>0>.
Константа 1 – F>15>.
Дизъюнкция (функция «ИЛИ», операция «ИЛИ», «ИЛИ», включающее «ИЛИ», соединение, логическое сложение) – БФ, таблица истинности (ТИ) которой соответствует F>14> в таблице хх.2. Обозначается с помощью знака «+» или «», например F=x+y (F=xy). Условное обозначение логического элемента (ЛЭ), реализующего дизъюнкцию (дизъюнктора), изображено на рисунке хх.1.а, а его временные диаграммы на рисунке хх.2.а.
Конъюнкция (функция «И», операция «И», «И», логическое умножение) – БФ, ТИ которой соответствует F>8> в таблице хх.2. Обозначается так же, как произведение в обычной алгебре или с помощью знака «&» («»), например F=x&y (F=xy). Условное обозначение ЛЭ, реализующего конъюнкцию (конъюнктора), изображено на рисунке хх.1.б, а его временные диаграммы на рисунке хх.2.б.
О
Рисунок хх.1 Условные обозначения ЛЭ:
а) дизъюнктор;
б) конъюнктор;
в) инвертор;
г) повторитель;
д) ЛЭ «»;
е) элемент «ИЛИ – НЕ»;
ж) элемент «И – НЕ»
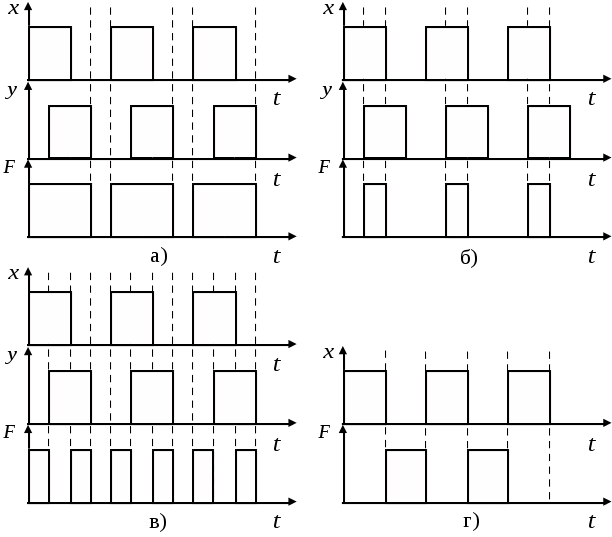
Рисунок хх.2 Временные диаграммы работы ЛЭ:
а) дизъюнктора; б) конъюнктора;
в) элемента «»; г) инвертора
трицание (инверсия) и повторение – БФ, ТИ которых были приведены в таблице хх.1. Отрицание обозначается чертой, которая ставится над переменной. Например, отрицание переменной х, читаемое «НЕ х», записывается в виде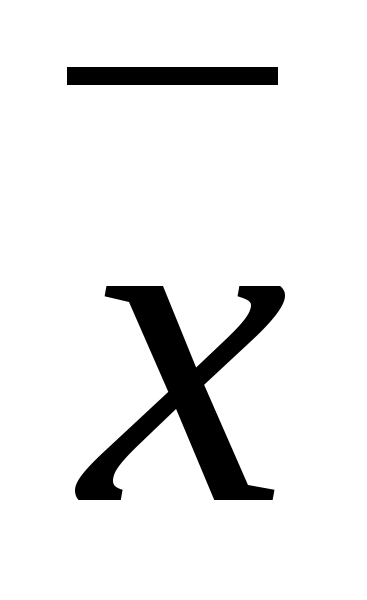 .
Условное обозначение ЛЭ, реализующего
отрицание (инвертора),
изображено на рисунке хх.1.в, а его
временные диаграммы на рисунке хх.2.г.
Условное обозначение ЛЭ, реализующего
повторение (повторителя),
изображено на рисунке хх.1.г.
.
Условное обозначение ЛЭ, реализующего
отрицание (инвертора),
изображено на рисунке хх.1.в, а его
временные диаграммы на рисунке хх.2.г.
Условное обозначение ЛЭ, реализующего
повторение (повторителя),
изображено на рисунке хх.1.г.
Сложение по модулю два (исключающее «ИЛИ») – БФ, ТИ которой соответствует F>6> в таблице хх.2. Обозначается с помощью знака «», например F=xy. Условное обозначение ЛЭ, реализующего сложение по модулю два, изображено на рисунке хх.1.д, а его временные диаграммы на рисунке хх.2.в.
Стрелка Пирса (функция «ИЛИ – НЕ») – БФ, ТИ которой соответствует F>1> в таблице хх.2. Обозначается с помощью знака «». Условное обозначение ЛЭ, изображено на рисунке хх.1.е.
Штрих Шеффера (функция «И – НЕ») – БФ, ТИ которой соответствует F>7> в таблице хх.2. Обозначается с помощью знака «/». Условное обозначение ЛЭ, изображено на рисунке хх.1.ж.
Равнозначность (эквивалентность) – БФ, ТИ которой соответствует F>9> в таблице хх.2. Обозначается с помощью знака «» или «~».
Импликация от х к у – БФ, ТИ которой соответствует F>11> в таблице хх.2. Обозначается с помощью знака «».
Хх.3 Понятие о СДНФ и СКНФ
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. Под элементарной конъюнкцией понимаются конъюнкции одной, двух, трех и т.д. переменных с отрицанием или без.
 .
.
ДНФ заданной БФ можно записать несколькими способами, причем одна запись будет отличаться от другой.
 .
.
Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций.
 .
.
Совершенной ДНФ (КНФ) называется такая ДНФ (КНФ), в состав каждой элементарной конъюнкции (дизъюнкции) которой входят все переменные, входящие в БФ.
Для нахождения СДНФ и СКНФ любой БФ существуют следующие алгоритмы.
Пусть БФ трех переменных F задана таблицей истинности (таблица хх.3).
Таблица хх.3 ТИ для F.
|
x |
y |
z |
F |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
выделяем наборы переменных, на которых функция равна 1;
записываем для этих наборов конъюнкции, при этом если переменная равна 1, то эта переменная записывается без отрицания, если же переменная равна 0, то такая переменная записывается с отрицанием;
объединяем элементарные конъюнкции знаками дизъюнкций;
полученное выражение будет являться совершенной ДНФ.
 .
.
Алгоритм нахождения СКНФ:
выделяем те наборы переменных, на которых функция равна 0;
из этих наборов переменных составляем дизъюнкции, учитывая то, что если переменная равна 0, то она записывается без отрицания, а если 1 – с отрицанием;
объединяем элементарные дизъюнкции знаками конъюнкций;
полученное выражение является совершенной КНФ.
 .
.
Рангом функции называется наибольшее число переменных, входящих в ДНФ.
Длиной функции называется число элементарных конъюнкций (дизъюнкций) входящих в эту функцию.
Универсальными БФ называются такие БФ, при помощи которых можно описать (представить) любое логическое выражение.
Кратчайшей называется функция, имеющая наименьший ранг и наименьшую длину.
Хх.4 Основные законы (аксиомы) БА
Булеву алгебру можно применять, зная три основные операции: «И», «ИЛИ», «НЕ». Однако полезно знать некоторые основные тождества (тавтологии), приведенные в таблице хх.4.
Таблица хх.4 Основные тождества БА
N |
Название |
Формулировка |
|
1 |
Коммутативности (переместительный) |
|
|
2 |
Ассоциативности (сочетательный) |
|
|
3 |
Дистрибутивности |
|
|
4 |
Соотношения абсорбции |
|
|
5 |
Теорема де Моргана |
|
|
6 |
Двойного отрицания |
|
|
7 |
Двойственности |
|
|
8 |
Пустого множества |
|
|
9 |
Универсального множества |
|
|
10 |
Склеивания |
|
|
11 |
Поглощения |
|
|
12 |
Следствие из 3 |
|
|
13 |
Обобщенный закон Клода- Шеннона |
|
Хх.5 Свойства функции сложения по модулю два
В таблице хх.5 приведены основные свойства функции сложения по модулю два.
Таблица хх.5 Свойства функции «»
N |
Название |
Формулировка |
|
1 |
Определение операции |
|
|
2 |
Коммутативности |
|
|
3 |
Ассоциативности |
|
|
4 |
Дистрибутивности |
|
|
5 |
«Закон де Моргана» |
|
|
6 |
Соотношения
для
|
|
Хх.6 Свойства стрелки Пирса и штриха Шеффера
Основные свойства стрелки Пирса и штриха Шеффера приведены в таблице хх.6.
Таблица хх.6 Свойства функций «» и «/»
|
N |
Название |
Формулировка |
|
1 |
Определение функции «» |
|
|
2 |
Определение функции «/» |
|
|
3 |
Коммутативности |
|
|
4 |
«Закон де Моргана» |
|
|
5 |
Соотношения
для
|
|
Следует отметить, что для обеих функций не справедливы законы ассоциативности и дистрибутивности.
Хх.7 Способы определения равносильности БФ
Существует три метода определения равносильности БФ:
при помощь ТИ;
при помощи законов алгебры логики;
приведением к СДНФ или СКНФ.
Пусть
даны три функции:  ;
;
 ;
;
 .
.
Определим равносильность данных функций.
Хх.7.1 Определение равносильности БФ с помощью ТИ
Таблица хх.7 ТИ для определения равносильности F>1>, F>2>, F>3>
-
x
y
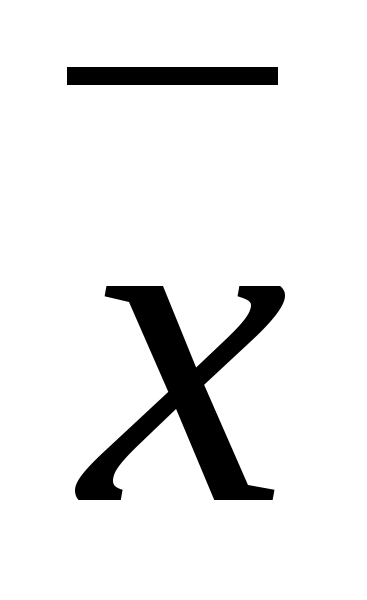
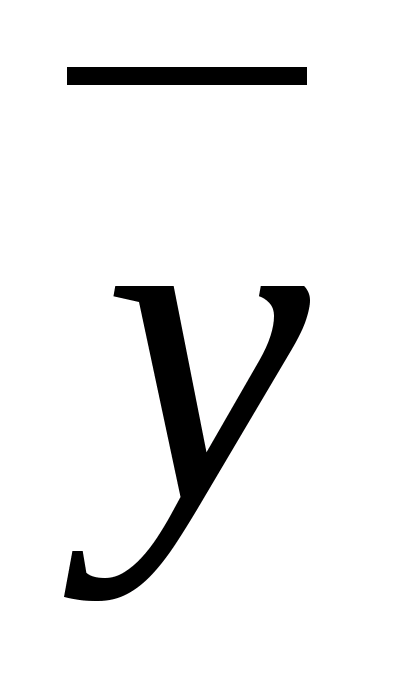
xy





0
0
1
1
0
0
1
1
1
1
0
1
1
0
0
1
0
1
1
1
1
0
0
1
0
0
0
0
0
0
1
1
0
0
1
0
0
1
1
1
Если несколько функций принимают на всех наборах одни и те же значения, то эти функции равносильны. Получаем, что F>1>= F>2>= F>3>.
Хх.7.2 Определение равносильности БФ при помощи логических преобразований
 .
.
 .
.
Получили, что F>1>= F>2>= F>3>.
Доказательство равносильности нескольких функций данным методом является самым сложным и требует очень хорошего знания свойств и законов БФ.
Хх.7.3 Определение равносильности БФ при помощи СДНФ
Сразу можно сделать вывод, что F>1> является СДНФ.
Любую БФ, равно как и ее ДНФ можно представить в виде СДНФ.
 .
.
 .
.
Получаем, что F>1>= F>2>= F>3>.
Хх.8 Выражение одних БФ через другие
Логическим элементом (ЛЭ) будем называть вентиль, описываемый какой либо простой БФ. Логической схемой (цепью, структурой) будем называть совокупность ЛЭ, соединенных между собой так, что выполняется заданный закон функционирования.
Задача синтеза сложных логических схем эквивалентна представлению сложных логических функций простыми функциями, описывающими работу ЛЭ. Одна из проблем синтеза заключается в выборе типов ЛЭ, из которых должны собираться логические схемы. Набор элементов должен допускать построение любой сколь угодно сложной структуры, т.е. представлять функционально полную систему операций.
Однако ясно, что построение одной логической схемы из множества ЛЭ разных типов бывает нецелесообразно. В некоторых случаях гораздо эффективнее логическая структура, составленная из однотипных элементов.
БФ, при помощи которых можно выразить любую другую БФ носят название функционально полных. При проектировании их еще называют базисом.
Из определений бинарных функций (таких как «», «», «/» и т.д.) можно заметить, что свойствами базиса обладают наборы «И – НЕ», «ИЛИ – НЕ», «И – ИЛИ – НЕ». Так мы их и будем называть: базис «И – НЕ», базис «ИЛИ – НЕ», базис «И – ИЛИ – НЕ». Но этими наборами не исчерпываются все возможные функционально полные системы. Существует также базис «», базис «/», базис « – И – 1» и другие.
Попытаемся выразить через стрелку Пирса и штрих Шеффера основные операции БА.
Дизъюнкция выражается следующим образом:
 ;
;
 .
.
Конъюнкция выражается как:
 ;
;
 .
.
Хх.9 Закон двойственности
Двойственной
формой БФ называется такая
форма, которая получается из заданной
формы путем замены дизъюнкции на
конъюнкцию и конъюнкции на дизъюнкцию.
Двойственная форма функции F
обозначается F*.
Например, для булевой функции трех
переменных
 двойственная форма запишется в виде
двойственная форма запишется в виде
 .
.
Закон двойственности: если две БФ тождественны между собой, то и их двойственные формы тоже тождественны.
Следует заметить, что двойственную форму необходимо отличать от инверсной.
Хх.10 Функциональная декомпозиция БФ
Любую заданную БФ можно представить двумя способами:
с помощью двух составляющих;
разложением на множители.
При этом используется метод разложения БФ по одной, двум и более переменным.
В
первом случае функция
 представляется в виде
представляется в виде
 .
.
Во втором – в виде
 .
.