Основные задачи термохимии. Использование калориметрических методов для определения теплот растворения солей

Московская городская олимпиада по химии

Реферат

Основные задачи термохимии. Использование калориметрических методов для определения теплот растворения солей.



ученика 11 класса

общеобразовательной школы №1303

(Химический лицей)

Кондакова Николая

Москва, 2000

Оглавление

1. Основные задачи термохимии 3

2. Чем обусловлен тепловой эффект реакции? 4

3. Калориметрическая установка 6

4. Вычисление t 8

5. Основной источник погрешности в результатах калориметрических опытов 8

6. Определение удельной теплоты растворения соли 9

7. Методики определения удельной теплоты растворения соли 9

8. Оглавление 10

Основные задачи термохимии

Термохимия, раздел химической термодинамики, включающий определение теплового эффекта реакции и установление его зависимости от физико-химических параметров. В задачу термохимии входит также измерение и вычисление теплот фазовых переходов, растворения, разбавления и других процессов, изучение теплоемкостей, энтальпий и энтропий веществ. Основным экспериментальным метод термохимии – калориметрия. Иногда используются некалориметрические методы (расчет тепловых эффектов из результатов измерения констант равновесия, эдс и т.п.), однако в этих случаях результаты обычно менее точны.

В 1840 году химик Гесс открыл закон, названный позднее его именем, этот закон дает возможность определять расчетным путем тепловые эффекты реакций по теплотам образования исходных веществ и продуктов или по теплотам их сгорания. Тем самым, открывая путь для определения тепловых эффектов реакций, которые трудно осуществимы, а иногда и невозможно. Необходимые для расчета стандартные теплоты образования H>обр>о собраны в фундаментальные термохимические справочники.

В середине XIX века Томсен и Бертло высказали идею, согласно которой химические реакции, происходящие без подвода энергии извне, протекают в направлении максимального выделения теплоты. Ими и их учениками были разработаны основные экспериментальные методики термохимии и измерены тепловые эффекты многих реакций.

Хотя в общем виде принцип Бертло-Томсена оказался неверен, но за термохимией сохранилась ведущая роль в исследовании возможности протекания химических реакций в заданных условиях. Так, уравнение H - TS=-RTlnK>p> являющееся обобщением первого и второго начал термодинамики (H – изменение энтальпии, S – изменение энтропии при химической реакции, T – температура, R – газовая постоянная), позволяет рассчитать константу равновесия K>p >любой реакции через тепловые величины.

Изменение энтальпии (тепловой эффект) очень просто может быть измерен в лаборатории. Обычно это делают, окружая зону реакции: при этом происходит энергообмен. Если реакция является экзотермической, то вода нагревается, если эндотермической – то охлаждается. Если измерить изменение температуры воды и если известна масса воды и ее удельная теплоемкость, то можно вычислить количество поглощенной или выделенной в процессе химической реакции энергии.

На рисунке 1 показан прибор, с помощью которого может быть получено более точное значение H, чем в довольно грубом расчетном методе. Этот прибор называется калориметрической бомбой и предназначен для определения теплоты сгорания вещества.

Для некоторых реакций можно непосредственно измерить H. Возьмем, к примеру, реакцию горения метана. Можно провести грубое измерение H этой реакции, используя обычное кухонное оборудование и газовую плиту.

Д

рисунок 1

1 термометр. 2 вода. 3 электрическая спираль для сжигания образца. 4 воздушная рубашка. 5 мешалка. 6 тигель с анализируемым образцом. 7 кислород под давлением. 8 бомба калориметра

ля других реакций это выполнить сложнее. Например, для реакции разложения CaCO>3> требуется температура свыше 800оС, что усложняет использование

воды для измерения передаваемой энергии. В таких

случаях изменение энтальпии определяется косвенно, с

использованием энтальпийных циклов.

Как уже было отмечено, калориметрия используется для определения тепловых эффектов реакций, в частности она используется и для определения теплот растворения солей или других соединений в воде 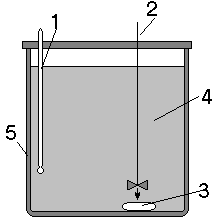или других растворителях. Это является одной из самых интересных задач термохимии, так как выделение теплоты при растворении солей может быть использовано для разогрева или охлаждения тех или иных объектов.

Чем обусловлен тепловой эффект реакции?

рисунок 2.

1 термометр. 2 мешалка с наконечником для пробивания ампул. 3 ампула. 4 калориметрическая жидкость. 5 калориметрическая оболочка


А чем, собственно говоря, определяется изменение теплового эффекта реакции.

Процесс образования растворов на молекулярном уровне можно представить следующим образом. Каждая группа молекул чистого вещества должна сначала перестроиться таким образом, чтобы молекулы были удалены друг от друга на расстояния, соответствующие конечной концентрации раствора. (Например, в разбавленном растворе метанола в воде молекулы метанола очень удалены друг от друга, а молекулы воды находятся почти так же близко друг к другу, как в чистой воде.) Далее системы с удаленными молекулами должны сблизиться, образовав раствор конечной плотности. Сначала индивидуальные вещества должны поглотить энергию, чтобы произошло разделение частиц; однако при сближении частиц «раздвинутых» систем при образовании раствора энергия выделяется. Смешение частиц увеличивает статический “беспорядок” системы, что сопровождается увеличением энтропии.

Для процессов растворения характерна склонность к самопроизвольному протеканию к отрицательному изменению энергии Гиббса в результате смешивания частиц растворителя и растворенного вещества.

Основные различия в поведении растворов зависят от баланса выделяемой и поглощаемой энергии, связанной с изменениями межчастичных расстояний. Величины H для процессов растворения отличаются друг от друга. Образование раствора является экзотермическим процессом (изменение энтальпии отрицательно), если при смешении частиц освобождается больше энергии, чем необходимо для первоначального разделения частиц. Если же для разделения деления частиц требуется больше энергии, чем освобождается при смешении, процесс растворения - эндотермичен (изменение энтальпии положительно). Поскольку энтальпийная функция дает вклад в изменение энергии Гиббса G=H-TS, можно ожидать, что именно для эндотермического процесса наиболее вероятна ограниченная растворимость; это в действительности подтверждается термодинамическими измерениями. Однако на молекулярном уровне эндотермический ход процесса растворения обусловлен тем, что однородные частицы в чистых жидкостях притягивают друг друга в смеси в среднем сильнее по сравнению с разнородными. Следовательно, для разделения однородных частиц в систему необходимо ввести больше энергии, чем выделится при сближении разнородных частиц в процессе смешения.

Приведенные рассуждения включают ряд допущений, в действительности поведение растворов часто значительно сложнее. Например, конечный раствор представляет собой систему с совершенно случайным распределением частиц, при рассмотрении которой была исключена возможность существования в растворе некоторой упорядоченной структуры. Если наличие упорядоченной структуры вносит свой вклад в образование раствора, то изменение энтропии будет иметь меньшее положительное значение, которое трудно поддается анализу. Тем не менее корреляция положительных отклонений от поведения идеальных растворов и ограниченной растворимости с энергиями притяжения между однородными частицами является достаточно хорошим первым приближением.

Образование раствора может продолжаться до тех пор, пока химические потенциалы компонентов заметно понизятся при переходе в раствор. Теоретическая модель процесса растворения объясняет понижение химического потенциала как результат разупорядочения при смешении частиц и влияния энергетических эффектов за счет притяжения между частицами. Если энергия притяжения между однородными частицами больше энергии притяжения между разнородными частицами, то снижение химического потенциала велико только для очень разбавленных растворов, а затем становится незначительным. Тогда можно предсказать, будут ли два вещества обладать высокой или низкой взаимной растворимостью; для этого необходимо только оценить степень притяжения между однородными частицами.

Теплоты испарения служат удобной и достаточно достоверной мерой энергии притяжения, хотя следует иметь в виду вклады других факторов, таких, как размеры молекул и специфические взаимодействия между частицами. В общем, два компонента будут обладать ограниченной взаимной растворимостью, если один из них характеризуется значительно большей теплотой испарения по сравнению с другим.

При смешении двух жидкостей могут наблюдаться всевозможные градации взаимной растворимости: от практически полной нерастворимости друг в друге (например, ртуть и вода) до смешения в любых соотношениях с образованием однородного раствора (например, этанол и вода). Промежуточное положение занимает смесь ограниченной взаимной растворимости. Смесь жидкостей А и В (например, анилин и вода) разделяется после взбалтывания на два слоя: насыщенный раствор А в В и насыщенный раствор В в А. Однако и в этом случае могут существовать области температуры и состава, в которых компоненты А и В образуют однородную смесь.

Термохимические изменения

Ввиду разнообразия в поведении растворы классифицируют в соответствии с их термодинамическими свойствами. С этой точки зрения различают идеальные и неидеальные растворы. Для большинства физико-химических расчетов необходимо знать теплоемкости веществ, участвующих в процессе, тепловые эффекты процессов растворения, фазовых превращений и химических реакций. Эти величины можно измерить экспериментально. При температурах, близких к комнатной (20-50оС), широко применяется калориметрический метод.

При калориметрических опытах величина и знак теплового эффекта Q процесса определяются по изменению температуры калориметра t:

(1)

где m>i> – масса исследуемого вещества, калориметра и вспомогательных устройств (мешалки, ампулы, термометра); c – удельные теплоемкости исследуемого вещества, калориметра и вспомогательных устройств; с>> - суммарная теплоемкость калориметрической системы. Уравнение (1) может быть записано

Q=(K+m>1>c>1>)t

где K – константа калориметра, то есть теплоемкость частей калориметра и вспомогательных устройств, участвующих в теплообмене, Дж/К; с>1> – теплоемкость содержимого калориметра; t – изменение температуры процесса, протекающего в условиях отсутствия теплообмена калориметра с окружающей средой.

Калориметр с изотермической оболочкой (диатермический) позволяет учесть теплообмен его с окружающей средой, что дает возможность вычислить изменение температуры t, соответствующее опыту без теплообмена.

Теплоемкость систему С называют производную dQ/dT. Теплоемкость газов и жидкостей зависит от температуры, а теплоемкость твердых веществ при средних и высоких температурах практически от нее не зависит. При расчетах часто использую теплоемкость.

Средней теплоемкостью однородного тела называют отношение подведенной теплоты к повышению температуры:

Средняя теплоемкость зависит от интервала температур (Т>2> – Т>1>). Зависимость между истинной и средней теплоемкостями выражается уравнением

При Т5о даже на совершенных калориметрах (при измерении с точностью 0,05%) не удается установить различия между истинной и средней теплоемкостью. Поэтому теплоемкость, определенную в результате изменения температуры калориметра на 2-3о, принимают за истинную и относят ее к температуре (Т>2>+Т>1>)/2. Теплоемкость однородного тела зависит от его массы:

С=сm или ,

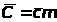где удельная теплоемкость вещества; m – масса вещества. Если масса равна молярной или атомной массе, то теплоемкость будет соответственно молярной или атомной. Если во время опыта давление в калориметрической системе остается постоянным (в калориметрах открытого типа оно равно атмосферному), то тепловой эффект процесса при постоянном давлении будет Q>р>, а теплоемкость С>р>.> >При термохимических изменениях процессам, сопровождающимся выделением теплоты (экзотермическим процессам), приписывается положительный знак. При выделении системной теплоты ее энтальпия убывает. Откуда Q>р>=-H. Если в уравнениях тепловой эффект обозначен Q или q, то следует применять термохимическую систему знаков.

Калориметрическая установка (диатермический калориметр).

Калориметрическая установка состоит из воздушного термостата и помещенного в нем калориметра. Термостат представляет собой бокс с застекленными стенками, в котором установлены нагреватель, вентилятор, термохимический и контактный термометры. Нагреватель выключается при помощи реле при достижении в боксе заданной температуры. В качестве нагревателя используется электрическая лампочка, обладающая малой тепловой инерцией. Температура в боксе поддерживается с точностью ±0,02°. Воздушная среда в боксе с постоянной температурой является изотермической оболочкой калориметра.

Калориметр состоит из калориметрического сосуда (полиэтиленовый стакан). Через отверстия в крышке бокса в калориметре крепятся стеклянная мешалка, термометр Бекмана, электронагреватель и ампула с исследуемым веществом. Калориметр устанавливается в боксе на столике, перемещающемся вертикально. Электронагреватель питается от электросети через стабилизатор и трансформатор. Число оборотов вентилятора и мешалки регулируют лабораторными автотрансформаторами. Напряжение в электронагревателе регулируют реостатом. Отсчеты времени производятся с помощью звукового сигнализатора, подающего сигналы через каждые 30 с. Тепловой баланс процесса в калориметрическом опыте выражается уравнением

где q—теплообмен калориметра с окружающей средой за период калориметрического опыта.

Если бы исследуемый процесс и выравнивание температуры в калориметре происходили мгновенно, то теплообмен со средой был бы равен нулю (q=0). В реальных условиях протекание процесса и выравнивание температуры требует времени, в течение которого калориметр получает от среды или отдает ей некоторое количество теплоты q. Величину q не вычисляют, но опыт проводят в калориметре так, чтобы на основании полученных данных можно было вычислить изменение температуры t (отличное от t`) того же процесса, но протекающего мгновенно без тепловых потерь. Калориметрический опыт следует начинать при условии, если система близка к состоянию теплового равновесия, характеризуемого не значительным температурным ходом (не более 0,04 град/мин). Это условие можно выполнить, установив температуру содержимого калориметра при работающей мешалке на 1—2° ниже температуры воздуха в боксе. При такой разности температур скорость поступления теплоты в калориметр от воздуха становится равной скорости отдачи теплоты за счет испарения воды, находящейся в калориметрическом сосуде, что обеспечивает тепловое равновесие системы. Если в исследуемом процессе наблюдается выделение теплоты, то в начальном периоде температура калориметра должна повышаться. Если в процессе наблюдается поглощение теплоты, то температура калориметра должна понижаться. При постоянной скорости изменения температуры производят 10—12 отсчетов по термометру Бекмана через каждые 30 с. Это — начальный период калориметрического опыта. Затем проводят определение теплового эффекта процесса. Температуру по термометру Бекмана непрерывно продолжают отсчитывать через те же промежутки времени. За счет выделения или поглощения теплоты в процессе происходит резкое изменение температуры. Это — главный период калориметрического опыта. По завершении главного периода вновь устанавливается равномерный ход температуры. Это — конечный период калориметрического опыта, в течение которого производят еще 12 — 15 отсчетов по термометру Бекмана. (Если во время калориметрического опыта очередной отсчет показания термометра был пропущен, то следует прочеркнуть и записать следующий под своим порядковым номером.)

В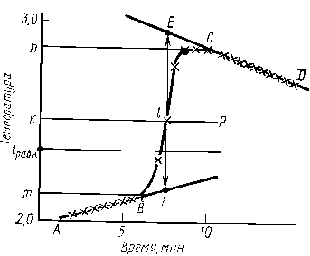ычисление t.

Типичный вид температурной кривой правильно поставленного калориметрического опыта при измерении экзотермического эффекта показан на рисунке 3. Величину t с учетом теплообмена можно рассчитать аналитическим или графическим способом.

П

Рисунок 3. Определение изменения температуры в ходе калориметрического опыта

ри графическом определении t на миллиметровой бумаге на оси абсцисс откладывают время в масштабе 1 мин = 1 см, на оси ординат — температуру, выбор масштаба которой зависит от величины t. При t1° 1°=10 см; t1° 1° — 5 см. После того как на график нанесены все экспериментальные точки, получается кривая ABCD. Участок АВ называется начальным периодом, ВС — главным, CD — конечным. Чтобы определить изменение температуры t, не искаженное теплообменом, происходящим в течение главного периода, продолжают АВ и CD до пересечения с вертикальной прямой EF. Для этого точки m и n, соответствующие начальной и конечной температурам главного периода, наносят на ось ординат. Через середину отрезка mn проводят линию КР. Пересечение этой линии с кривой ВС дает точку 1, определяющую положение прямой EF. Отрезок EF и будет равен t, отрезок mn=t`. Чем меньше температурный ход в начальном и конечном периодах, тем меньше потери теплоты за счет теплообмена и тем ближе t` к t. Если температурный ход содержимого калориметра при работающей мешалке равен нулю, то это состояние соответствует t>равн>. Характер линии ВС зависит от условий протекания теплового процесса (например, от размешивания), наклон линий АВ и CD зависит от характера теплообмена с окружающей средой. Таким образом, по виду кривой ABCD можно судить о качестве проведенного опыта.

Так как определение поправки: на теплообмен с внешней средой всегда связано с некоторой неточностью, то надо выбирать условия, при которых значение q было мало по сравнению с величиной q>p>. Это достигается, если в ходе опыта отклонения системы от состояния теплового равновесия невелики, что характеризуется соотношением m<t>равн><n. Указанное условие соблюдается, если температурный ход в начальном и конечном периодах имеет противоположный знак, а по абсолютной величине ход температуры в начальном периоде должен быть несколько больше, чем в конечном периоде. Чем меньше t, тем меньше должен быть ход температуры в начальном и конечном периодах.

Основной источник погрешности результатов калориметрических опытов.

Работа производится на установке упрощенного типа, позволяющей при тщательном проведении калориметрических опытов и правильно выбранных условиях (продолжительность опыта не должна превышать 5 мин) получать результаты с погрешностью около ±1%. Главными факторами, определяющими точность результата, будут погрешности t, так как ошибки взвешивания не превышают сотых долей процента. В калориметрической установке температуры измеряют при помощи термометра Бекмана, точность отсчета по которому составляет в данных условиях около ±0,005°, поэтому возможная погрешность в определении t составит ±0,01°. Относительная ошибка, вносимая в результат за счет неточности измерения температур, выражается отношением погрешности к t>оп>. Так, при указанной точности измерений по термометру Бекмана и t1° погрешность t>oп> составляет ±1%, при t=0,l° она равна ±10%.

Определение удельной интегральной теплоты растворения соли.

В работе следует определить суммарную теплоемкость системы и удельную интегральную теплоту q растворения соли.

Тепловой эффект, сопровождающий растворение твердого вещества в жидкости и отнесенный к 1 г растворяемого вещества, называют удельной теплотой растворения. Тепловой эффект, отнесенный к 1 моль растворяемого вещества, называют молярной теплотой растворения. Теплота растворения зависит от концентрации раствора. Различают интегральную теплоту растворения – тепловой эффект, сопровождающий процесс растворения 1 моль (молярная) или 1 г (удельная) вещества в данном количестве вещества в бесконечно большом количестве раствора заданной концентрации. Интегральные теплоты растворения определяют экспериментально, а диффиринциальные вычисляют по зависимости интегральных теплот растворения от концентрации раствора:

(2)

Первый вариант. Суммарная теплоемкость системы с>> определяется электрическим методом.

Последовательность выполнения работы.

1. Определение изменения температуры t>раств> при растворении исследуемого вещества и продолжительности главного периода. В стакан калориметра залить 200 мл воды. Отвесить на технических весах 2 г тщательно измельченного исследуемого вещества, перенести его во взвешенную на аналитических весах ампулу и вновь взвесить ее. Укрепить ампулу в крышке термостата, погрузив в воду. После одиннадцатого отсчета разбить пробойником ампулу, не прерывая записи температуры через каждые 30 секунд. Температура воды при эндотермическом растворении сначала резко падает (главный период), затем начинает равномерно расти, приближаясь к средней температуре системы. Отсчетом температуры, с которой начинается ее равномерное повышение, кончается главный период калориметрического опыта и начинается конечный период.

Определить графически изменение температуры t>раств> и продолжительность главного периода .

2. Определение суммарной теплоемкости с>> системы. Суммарная теплоемкость калориметрической системы зависит от условий проведения калориметрической системы зависит от условий проведения калориметрического опыта, поэтому ее следует определять при условиях, близких к условиям проведения калориметрического опыта, поэтому ее следует определять при растворении соли (определение t>раств>). Наиболее важно добиться одинаковой продолжительности главного периода  и одинаковых абсолютных величин t в обоих опытах. Изменение температуры t>э> содержимого калориметра зависит от силы тока при пропускании его через нагреватель. Чтобы установить силу тока, при t>э> будет равно t>раств>, необходимо провести три опыта, пропуская в нагреватель, погруженный в раствор, ток силой I>1>=1 A, I>2>=2 A, I>3>=3 A в течение времени =. Построить график t>э>=f(I) и определить интерполяцией силу тока, при котором t>э>=t>раств>.

Построить график t>э>=f(I): отложить по оси ординат температуру 0,1о=10мм, по оси абсцисс – силу тока 1 А=50мм и определить силу тока при t>э>=t>раств>. Установить с помощью реостата силу тока, проходящего через нагреватель, записать соответствующее показание вольтметра Е. Вычислить С>> по уравнениям С=сm или 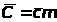, подставив в него найденные значения I, Е, Δt>э>, Δτ. Вычислить q по уравнению (2).

Работа 3. Определение интегральной теплоты растворения соли при образовании концентрированного раствора

В работе необходимо определить теплоту растворения соли с образованием раствора, концентрация которого близка к насыщению. Если конечная концентрация раствора близка к насыщению, то скорость растворения настолько замедляется в конце процесса, что прямое определение теплоты 1растворения Q становится невозможным. Это подтверждается уравнением

(3)

где dC/dt—скорость растворения; К—константа скорости растворения; С>нас> и С>х>—концентрация соли в насыщенном растворе и в момент времени . Скорость растворения в конце процесса настолько замедляется (С>нас>—С>х>0), что прямое определение интегральной теплоты растворения Q становится невозможным. Теплоту растворения в этом случае определяют косвенным путем.

Теплоту образования концентрированного раствора определяют в две стадия. Каждая стадия протекает с достаточно большой скоростью. В первой стадии определяют теплоту растворения Q>1> соли при образовании раствора концентрации m>2> меньшей, чем m>1>, а во второй стадии — теплоту разбавления концентрированного раствора Q>2> концентрации m>1> до концентрации m>2>. Тогда по закону Гесса

Q=Q>1>-Q>2 >(4)

Величину Q>1> вычисляют по зависимости интегральных теплот растворения от концентрации, используя справочные данные. Значение Q>2> определяют экспериментально и вычисляют по уравнению

(5)

где С>>—суммарная теплоемкость системы; t>раств> — изменение температуры в процессе разбавления; М—молекулярная масса соли; g - навеска соли, содержащейся в исходном объеме концентрированного раствора.

Список литературы:

    Козырева Н.А., Кудряшов И.В. Практикум по органической химии 4-е издание. изд. “Высшая школа” 1986г. 495 с.

    Химия и жизнь (Солтеровская химия) Часть I Понятия химии: Пер. с англ. – М.: РХТУ им. Д.И.Менделеева, 1997 – 337 с.

    Калориметрия. Теория и практика: Пер. с англ./В.Хеммингер, Г.Хене. – М.: Химия, 1990 – 176 с.

    Химическая энциклопедия т.4 с. 442 издательство “Большая Российская энциклопедия”., 1995 - 639 с.: ил.