Формирование портфеля ценных бумаг коммерческого банка

Аннотация

Величко О.С. Формирование портфеля ценных бумаг коммерческого банка.– Челябинск: ЮУрГУ, ЭиУ, 2002, 126 с. 23 илл. Библиография литературы – 30 наименований.

После анализа теоретического материала по формированию портфеля ценных бумаг и математических методов оптимизации структуры предложена двухуровневая схема, состоящая из формирования портфелей ценных бумаг (акций, облигаций) и последующим их объединением. Для портфеля акций была предложена индексная модель Шарпа и модель оценки финансовых активов для акций, для портфеля облигаций и совокупного портфеля – модель Марковица.

Произведены расчеты по формированию и оптимизации портфеля ценных бумаг для АБ «Дорожник» на апрель 2002г. по предложенной схеме. Применение данной схемы позволило бы получить прибыль в 412468 руб.. Доходность переоценки расчетного портфеля за апрель составила 8,17%.

Содержание

     Введение 6
1   Портфельное инвестирование 9
1.1   Основные принципы формирования портфеля инвестиций 9
1.2   Характеристика основных видов ценных бумаг и оценка          их доходности 12
1.2.1   Акции 13
1.2.2   Облигации 16
1.3   Рынок ценных бумаг как часть финансового рынка 21
1.3.1   Деятельность коммерческого банка на рынке ценных бумаг 22
1.4   Модели портфельного инвестирования 27
1.5   Структура инвестиционного процесса 31

2   Методики формирования оптимальной структуры портфеля 37
2.1   Модель Марковица 37
2.2   Модель Блека 44
2.3   Индексная модель Шарпа 45
2.4   Модель Тобина с безрисковым активом 49
2.4.1   Алгоритм Элтона-Грубера-Падберга 53
2.5   Модель оценки финансовых активов 54
2.6   Теория арбитражного ценообразования 62

3   Формирование и оптимизация портфеля ценных бумаг       (на примере АБ «Дорожник») 65
3.1   Формирование оптимальной структуры портфеля         государственных облигаций 66
3.2   Формирование оптимальной структуры портфеля акций 73
3.3   Формирование оптимальной структуры совокупного         портфеля ценных бумаг 82
3.4   Анализ результатов формирования порфеля ценных бумаг 87
4   Безопасность жизнедеятельности 93
     Заключение 98
     Литература 103
Приложение А Исходные данные для формирования портфеля                           государственных облигаций 105
Приложение Б Исходные данные для формирования портфеля акций 108
Приложение В Данные для формирования совокупного портфеля                           ценных бумаг 116
Приложение Г Данные для определения динамики стоимости                           сформированного портфеля 119
Приложение Д Графики цен закрытия акций (РТС) на период                         составления портфеля 122

Введение

Многие коммерческие банки в настоящее время имеют достаточно большой объем свободных средств, которые возможно как инвестировать в различные виды деятельности, так и направить на приобретение ценных бумаг. При осуществлении инвестирования в ценные бумаги банк, как и любой другой инвестор, сталкивается с различными целями инвестирования.

Именно портфель ценных бумаг является тем инструментом, с помощью которого может быть достигнуто требуемое соотношение всех инвестиционных целей, которое недостижимо с позиции отдельно взятой ценной бумаги, и возможно только при их комбинации.

Портфели ценных бумаг коммерческих банков являются частью взаимосвязанной системы портфелей более высокого уровня. Функционирование всей системы портфелей подчинено интересам обеспечения устойчивости и рентабельности института, обеспечения устойчивости всей финансовой системы.

Этими факторами обусловлен выбор темы дипломного проекта – формирование портфеля ценных бумаг коммерческого банка.

Объектом исследования является акционерный банк «Дорожник». Несмотря на то, что в нем временно прекращены операции по инвестированию средств в ценные бумаги, в будущем планируется восстановить работу отдела ценных бумаг в полном объеме. Поэтому целью данного дипломного проекта является обоснование методик портфельного инвестирования, то есть формализованного подхода к составлению портфеля ценных бумаг, который банк может применить в своей дальнейшей деятельности.

Для полного раскрытия выбранной темы были поставлены следующие задачи:

1. Исследовать основные теоретические предпосылки формирования портфеля ценных бумаг.

2. Провести обзор методик портфельного инвестирования.

3. Выбрать методику для практического применения.

4. Определить структуру портфеля ценных бумаг.

5. Оценить эффективность применения данного подхода.

В соответствии с этими задачами построены главы и параграфы данной работы. Первая глава посвящена обзору теории портфельного инвестирования. Описаны основные ценные бумаги, рынок на котором они обращаются, его участники. Особое внимание уделено коммерческим банкам: рассмотрен, в частности, механизм торгов ценными бумагами на биржах. Также в первой главе рассматривается структура инвестиционного процесса, которая далее применяется при практическом составлении порфеля ценных бумаг.

Основное внимание при формировании портфеля в данном дипломном проекте уделяется оптимизации его структуры. Поэтому вторая глава полностью посвящена обзору математических моделей, применяемых для этой цели. Для того чтобы сформировать оптимальный портфель ценных бумаг необходимо разработать инвестиционную стратегию, которая основывается на анализе доходности от вложения, времени инвестирования и анализе возникающих при этом риске.

Тема формирования и оптимизации портфеля ценных бумаг стала актуальной с появлением самих ценных бумаг, особенно по мере возникновения различных их форм. Как примирить стремление инвестора к получению максимальной прибыли от ценных бумаг со стремлением иметь наименьший риск получения убытка – главный вопрос рассматриваемой проблемы. Решение этого вопроса и есть решение задачи оптимизации портфеля ценных бумаг инвестора.

В виду того, что большинство портфельных теорий взаимосвязано, структура второго раздела построена таким образом, чтобы каждая последующая модель основывалась на постулатах предыдущей или учитывала ее выводы.

Таким образом, в двух первых главах сформулирована методологическая база для научного обоснования аппаратов и критериев формирования инвестиционной стратегии и созданы предпосылки для формирования научного подхода к формированию портфеля ценных бумаг.

В третьей главе проводится практическое применение методик, рассмотренных во второй главе и выбранных для расчетов. Приводится также обоснование этого выбора, основанное на анализе ситуации, в которой находится объект исследования, и соотношении затрат и приобретаемых выгод.

Результатом практического расчета является формирование оптимальной структуры портфеля ценных бумаг, что соответствует одной из поставленных задач. Все расчеты проведены на основе практических данных. В заключение проводится анализ эффективности применения выбранных методик и оценка полученного дохода.

В дипломной работе использованы материалы экономической и финансовой литературы, тематических материалов периодических изданий, а также сведения о биржевых котировках и аналитический материал по состоянию рынка.

Для решения поставленных задач в работе применены различные экономико-статистические методы.

В последние десятилетия использование портфельной теории значительно расширилось. Все большее число инвестиционных менеджеров, управляющих инвестиционных фондов применяют ее методы на практике, и хотя у нее имеется немало противников, ее влияние постоянно растет не только в академических кругах, но и на практике, включая российскую. Присуждение Нобелевских премий по экономике ее создателям и разработчикам является свидетельством этого.

1Портфельное инвестирование

1.1Основные принципы формирования портфеля инвестиций

Под инвестированием в широком смысле понимается любой процесс, имеющий целью сохранение и увеличение стоимости денежных или других средств. Средства, предназначенные для инвестирования, представляют собой инвестиционный капитал. С течением времени этот капитал может принимать различные конкретные формы. Тот или иной конкретный вид инвестиционного капитала называется инвестиционным активом.

Из определений инвестирования и инвестиционных активов, данных выше, видна важнейшая роль двух факторов: времени и стоимости. Важнейший принцип инвестирования состоит в том, что стоимость актива меняется со временем.

Со временем связана еще одна характеристика процесса инвестирования – риск. Хотя инвестиционный капитал имеет вполне определенную стоимость в начальный момент времени, его будущая стоимость в этот момент неизвестна. Для инвестора эта будущая стоимость есть ожидаемая величина.

Под инвестиционным портфелем понимается некая совокупность ценных бумаг, принадлежащих физическому или юридическому лицу, либо юридическим или физическим лицам, выступающая как целостный объект управления. Обычно на рынке продается некое инвестиционное качество с заданным соотношением Риск/Доход, которое в процессе управления портфелем может быть улучшено.

Портфель представляет собой определенный набор из корпоративных акций, облигаций с различной степенью обеспечения и риска, а также бумаг с фиксированным доходом, гарантированным государством, т.е. с минимальным риском потерь по основной сумме и текущим поступлениям. Теоретически портфель может состоять из бумаг одного вида, а также менять свою структуру путем замещения одних бумаг другими. Однако каждая ценная бумага в отдельности не может достигать подобного результата.

Основная задача портфельного инвестирования – улучшить условия инвестирования, придав совокупности ценных бумаг такие инвестиционные характеристики, которые недостижимы с позиции отдельно взятой ценной бумаги, и возможны только при их комбинации.

Только в процессе формирования портфеля достигается новое инвестиционное качество с заданными характеристиками. Таким образом, портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске.

Банки, покупая те или иные виды ценных бумаг, стремятся достичь определенных целей, к основным из которых относятся:

• доходность вложений;

• рост вложений;

• ликвидность вложений;

• безопасность вложений.

Инвестиционные ценные бумаги приносят доход в виде процентного дохода и прироста рыночной стоимости. Доходность портфеля – характеристика, связанная с данным промежутком времени. Длина этого периода может быть произвольной. На практике используют обычно нормированную доходность, т.е. доходность, приведенную к выбранному базисному периоду, обычно году.

Доходность портфеля за период можно вычислять по формуле:

, (1)

где r_>p> – доходность портфеля за определенный период времени, %;
W_>0> – стоимость портфеля в начале периода, руб.;
W_>1> – стоимость в конце периода, руб.

Управление портфелем коммерческого банка заключается в поддержании баланса между ликвидностью и прибыльностью. Сумма принадлежащих банку ценных бумаг непосредственно связана с умением банка управлять ценными бумагами и зависит от размера банка.

Ликвидность ценной бумаги можно оценить по агрегированному показателю ликвидности:

, (2)

где L_>A> – агрегированный показатель ликвидности ценной бумаги;

N_>bid>, N_>ask> – количество заявок на покупку и продажу соответственно, шт.;

P_>bid>, P_>ask> – средняя цена покупки и продажи соответственно, руб.

Под безопасностью вложений понимается неуязвимость инвестиций от различных потрясений на фондовом рынке, стабильность получения дохода и ликвидность. Безопасность всегда достигается в ущерб доходности и росту вложений. Оптимальное сочетание безопасности и доходности регулируется тщательным подбором и постоянной ревизией инвестиционного портфеля.

Риск – это стоимостное выражение вероятностного события ведущего к потерям. В мировой практике существует множество классификаций рисков. Наиболее известная из них – это деление риска на систематический и несистематический.

Систематический риск – риск кризиса финансового рынка в целом. Этот вид риска является недиверсифицируемым. Анализ систематического риска сводится к оценке того, стоит ли вообще иметь дело с портфелем ценных бумаг.

Несистематический риск связан с конкретным финансовым инструментом, данный вид риска может быть минимизирован за счет диверсификации. Исследования показали, что если портфель состоит из 10-20 различных видов финансовых инструментов, включенных с помощью случайной выборки из имеющегося на финансовом рынке набора, то несистематический риск может быть сведен к минимуму. Уровень несистематического риска – это оценка качества данного финансового инструмента.

По уровню риска виды ценных бумаг располагаются следующим образом исходя из принципа: чем выше доходность, тем выше риск, и чем выше гарантированность ценной бумаги, тем ниже риск (рисунок 1.1).

Одним из традиционных методов оценки и управления риском считается статистический метод. Основными инструментами статистического анализа являются – дисперсия, стандартное отклонение, коэффициент вариации. Суть этого метода состоит в анализе статистических данных за возможно больший период времени.

Хеджирование – это метод, основанный на страховании ценовых потерь на физическом рынке по отношению к фьючерсному или опционному рынку. Механизм хеджирования состоит в том, что участник рынка занимает в каждый момент времени прямо противоположные позиции.

1.2Характеристика основных видов ценных бумаг и оценка
их доходности

В общем виде ценные бумаги представляют собой титулы собственности, т.е. такие юридические документы, которые свидетельствуют о праве их владельца на доход или на имущество.

На фондовой бирже обращаются две категории ценных бумаг:

1. Долевые капитальные ценные бумаги, которые представляют непосредственно долю их владельца в собственности. Таким биржевым товаром являются акции.

2. Долговые ценные бумаги, обычно с твердо фиксированной процентной ставкой и обязательством возврата капитальной суммы долга к определенной дате в будущем. Основным биржевым товаром среди них являются облигации.

1.2.1Акции

Акцией признается ценная бумага, удостоверяющая право ее держателя (акционера) на получение части прибыли акционерного общества (АО) в виде дивидендов, на участие в управлении делами АО и на часть имущества, оставшегося после ликвидации АО. Право на выпуск акций имеют только акционерные общества. Акции выпускаются без установленного срока обращения.

У обыкновенных акций существует несколько видов стоимости. Каждая из них описывает определенное свойство рассматриваемой акции с точки зрения бухгалтерского учета, инвестирования, формирования курсов.

Номинальная стоимость – эта стоимость обозначает объявленную, или нарицательную, стоимость одной акции. Она не является мерой измерения каких-либо свойств акции и, таким образом, за исключением бухгалтерского учета, является относительно бесполезной.

Ликвидационная стоимость – является показателем того, что компания в состоянии представить на аукцион в том случае, если ей придется прекратить свою деятельность. После обыкновенной или аукционной продажи активов по самой выгодной цене из всех возможных , после погашения обязательств и осуществления платежей владельцам привилегированных акций остается сумма, известная как ликвидационная стоимость компании.

Рыночная стоимость – вид стоимости наиболее легок для исчисления, поскольку рыночная стоимость просто представляет доминирующий на рынке курс акций. По существу, рыночная стоимость является показателем того, как участники рынка в целом оценили стоимость одной акции. Умножив рыночную стоимость одной акции на количество имеющихся в обращении акций компании, можно также получить рыночную стоимость самой компании.

Рыночная цена – это цена, по которой акция продается и покупается на вторичном рынке. Рыночная цена обычно устанавливается на торгах на фондовой бирже и отражает действительную цену акции при большом объеме сделок.

Основной характеристикой акции является ее курсовая стоимость (курс акции). Под курсом акции понимается относительная величина, показывающая, во сколько раз текущая стоимость акции (по которой ее можно приобрести в настоящее время на рынке) больше номинала:

, (3)

где К – курс акции, руб.;

Р – рыночная цена, руб.;

N – номинальная цена, руб.

Показатель, отражающий среднюю цену акций и других ценных бумаг по определенной совокупности компаний, называется биржевым индексом. Индекс позволяет инвесторам, вкладывающим деньги в ценные бумаги, оценивать состояние как фондового рынка в целом, так и надежность собственных активов.

Основной характеристикой акции, характеризующей ее инвестиционную ценность, является ее совокупная доходность. Она находится по формуле:

_> >, (4)

где _> > – ставка дивиденда (%), которая зависит от суммы выплаченного по итогам года дивиденда – D_>e>, руб.;

K = (К_>2> – К_>1>) – изменение курсовой стоимости (разница между курсом на текущий момент К_>2> и курсом, по которому акция была приобретена К_>1>) – в долях единицы;

N – номинал акции, руб.

Иногда доходность находится для конкретного периода, в этом случае изменение курсовой стоимости находится по формуле:

_> >, (5)

где Р_>1> – рыночная стоимость на начало периода, руб.;

Р_>2> – рыночная стоимость на конец периода, руб.

Доходность служит исходной величиной для расчета более общей характеристики акции – чистой прибыли приобретения:

_> >, (6)

где P – рыночная стоимость на момент приобретения акции, руб.

Однако реальный курс акций различных эмитентов в каждый момент времени обычно отличается от действительной стоимости акции, так как на него дополнительно влияют факторы спроса и предложения фондового рынка.

В связи с тем, что интерес инвесторов к рыночному курсу выпуска акций компании постоянен, рыночная стоимость одной акции, как правило, является важным показателем для большинства инвесторов. Он должен быть использован при разработке инвестиционной политики и программ инвестирования.

Инвестиционная стоимость является, очевидно, наиболее важным показателем для акционера-инвестора, так как она указывает на ценность, которую инвестор приписывает ценной бумаге, но фактически представляет собой оценочную стоимость, по которой данная ценная бумага должна реализоваться на фондовом рынке.

Причины, которые объясняют большую привлекательность акций для инвесторов это:

• возможность получения по ним значительной прибыли. Рыночный курс акции обычно отражает потенциал прибыльности компании, поэтому при процветании компании процветают и инвесторы. Увеличение прибыли, в свою очередь, превращается в рост курсов акций (прирост капитала) и является важнейшей частью доходов от акций;

• способность быть высоколиквидными. Обыкновенные акции легко купить и продать, а затраты на проведение операций с ними малы; но, кроме того, сведения о курсах и информация о состоянии рынка распространяются в новостях и средствах массовой информации.

• курс одной обыкновенной акции достаточно низок, поэтому ее покупка вполне доступна большинству индивидуальных вкладчиков и инвесторов.

Однако существуют некоторые недостатки инвестирования в обыкновенные акции.

• рискованный характер ценной бумаги.

• трудно проводить оценку обыкновенных акций и последовательно отбирать те из них, которые имеют самые интересные перспективы, так как прибыли и динамика доходности акций подвержены широким колебаниям.

1.2.2Облигации

Облигация – ценная бумага, удостоверяющая внесение ее владельцем денежных средств и подтверждающая обязательство возместить ему номинальную стоимость этой ценной бумаги в предусмотренный в ней срок с уплатой фиксированного процента (если иное не предусмотрено правилами выпуска).

Основные отличия облигации от акции:

• облигация приносит доход только в течение строго определенного, указанного на ней срока;

• в отличие от ничем не гарантированного дивиденда по простой акции облигация обычно приносит ее владельцу доход в виде заранее установленного процента от нарицательной стоимости;

• облигация акционерного общества не дает права выступать ее владельцу в качестве акционера данного общества.

Доход по облигациям обычно ниже дохода по акциям, но он более надежен, так как в меньшей степени зависит от ситуации на рынке и циклических колебаний в экономике.

Сегодня в России можно встретить несколько типов этих ценных бумаг: облигации внутренних (государственных) и местных (муниципальных) займов, а также облигации предприятий и акционерных обществ.

Номинальная цена облигации служит базой при дальнейших перерасчетах и при начислении процентов. Кроме нее облигации имеют выкупную цену, которая может совпадать, а может и отличаться от номинальной в зависимости от условий займа. Кроме этого облигация имеет рыночную цену, определяемую условиями займа и ситуацией, сложившейся в текущий момент на рынке облигаций. Курс облигации – это значение рыночной цены, выраженное в процентах к номиналу. Если облигации продаются ниже номинала, а погашаются по номиналу, говорят что продажа производится "с дисконтом". Если облигации продаются по номиналу, а погашаются с начислением дополнительных процентов, говорят, что облигации погашаются "с премией". Иногда ежегодные начисления процентов комбинируются с дисконтом или премией.

Если по облигации предполагается периодическая выплата доходов, то он обычно производится по купонам. В зависимости от условий выпуска облигации- купонный доход может выплачиваться ежеквартально, раз в полгода или ежегодно.

Хотя по своей экономической сути все виды государственных ценных бумаг есть долговые обязательства, на практике каждая самостоятельная государственная ценная бумага получает свое собственное название, позволяющее отличать ее от других облигаций.

Основными государственными ценными бумагами являются следующие:

• государственные краткосрочные бескупонные облигации (ГКО);

• облигации федерального займа с переменным купонным доходом
  (ОФЗ-ПК);

• облигации федерального займа с постоянным купонным доходом
  (ОФЗ-ПД);

• облигации федерального займа с фиксированным доходом (ОФЗ-ФД);

В таблице 1.1 приведены характеристики этих ценных бумаг.

Цена облигации формируется под воздействием спроса и предложения со стороны инвесторов. При этом, однако, цена облигации не является абсолютно случайной, а колеблется около своего естественного значения, своей внутренней стоимости.

Таблица 1.1 – Спецификация некоторых видов государственных облигаций

Наименование	ГКО	ОФЗ-ПК	ОФЗ-ПД	ОФЗ-ФД
Эмитент	Министерство финансов РФ
Форма эмиссии	документарная с обязательным централизованным хранением
Вид облигации	именная бескупонная	именная купонная	именная купонная	именная купонная
Валюта займа	рубль	рубль	рубль	рубль
Номинал	1000 рублей	1000 рублей	1000 рублей	10 рублей
Срок обращения	до 1 года	от 1 года до 5 лет	от 1 года до 30 лет	более 4 лет
Частота выплат по купону	–	2 или 4 раза в год	1 раз в год	4 раза в год
Размещение и обращение	ММВБ	ММВБ	ММВБ	ММВБ

С точки зрения инвестора, облигация является обещанием инвестора уплачивать эмитенту определенную сумму денег. Таким образом, обещанный денежный поток по облигации описывается следующим образом: С_>1>, C_>2>, C_>3>,… C_>t>. Где С_>1>, C_>2>, C_>3>,… C_>t> – обещанные платежи по облигации (обычно С_>1> = C_>2> = C_>3 >=…= C_>t> – купонные платежи, а в платеж C_>t> включен также возврат номинальной стоимости облигации (N), т.е. C_>t> = С + N). При определении того, какой должна быть цена облигации, инвестор должен дисконтировать ожидаемые платежи и просуммировать их, т.е. вычислить чистую текущую стоимость (NPV) потока платежей. Если платежи происходят регулярно с периодичностью раз в год, то:

_> > (7)

При этом инвестор должен выбрать соответствующую норму дисконтирования (r) с учетом своих инвестиционных предпочтений и воспринимаемого риска.

Дюрация – взвешенное среднее сроков времени до наступления оставшихся платежей. Формула для вычисления дюрации (D) выглядит следующим образом:

_> >, (8)

где PV(C_>t>) – приведенная стоимость платежей, которые будут получены в момент времени t, руб.;

P_>0> – текущий рыночный курс облигаций, руб.;

T – срок до погашения облигации, дней.

Дюрация связана со сроком облигации до погашения, но зависит также от купонных платежей. По дисконтным облигациям (с нулевым купонным платежом) дюрация равна сроку обращения облигации. По купонным облигациям дюрация всегда меньше срока обращения. Важно подчеркнуть, что дюрация зависит также от того, какова требуемая норма доходности по облигациям.

В практической деятельности довольно часто возникает необходимость в определении финансовой эффективности облигационного займа. Последнее сводится к определению доходности облигации.

Доходом по бескупонным облигациям выступает дисконт, т.е. разница между ценой реализации (при погашении эта цена равна номиналу облигаций) и ценой их приобретения при первичном размещении или вторичном рынке.

При этом их доходность (доходность к погашению) рассчитывается по формуле простых процентов:

_> >, (9)

где Y_>s> – доходность к погашению по формуле простых процентов, %;

N – номинал облигации, руб.;

P – цена облигации, руб.;

t – количество дней до погашения.

Облигации с неизвестным (переменным) купонным доходом дают его владельцам право на периодическое получение процентного (купонного) дохода. При этом, здесь возможно также получение дисконта, если цена приобретения облигаций будет меньше цены их реализации, в том числе при погашении по номиналу.

В случае ОФЗ-ПК размеры каждого купона объявляются непосредственно перед началом соответствующего купонного периода исходя из текущей доходности выпусков ГКО, которые погашаются примерно в одно время с датой выплаты этого купона.

Общая формула доходности и величина накопленного купонного дохода определяется аналогично облигациям с известным купонным доходом. Для определения доходности используются оценки неизвестных купонов. При этом предполагается, что все неизвестные купоны равны между собой.

Облигации с известным купонным доходом (размеры которых заранее объявляются эмитентом) являются ценными бумагами, дающими его владельцам право на периодическое получение процентного (купонного) дохода. В случае ОФЗ-ПД размеры всех купонов определяются как постоянная величина на весь период до погашения. В случае ОФЗ-ФД величина купонного дохода устанавливается при выпуске как фиксированная величина, которая может различаться для различных периодов выплат.

При приобретении облигаций их покупатель должен выплатить прежнему владельцу помимо собственно цены («чистой» цены) облигаций также и величину накопленного купонного дохода, которая рассчитывается следующим образом:

_> >, (10)

где A – величина накопленного купонного дохода, руб.;

C_>1> – размер ближайшего купона, руб.;

T – длительность текущего купонного периода, дни;

t_>1> – количество дней до ближайшей купонной даты.

При этом их доходность (доходность к погашению) рассчитывается по формуле сложных процентов:

_> >, (11)

где Y_>e> – эффективная доходность (в процентах, с точностью до сотых процента);

N – номинал облигации, руб.;

P – цена облигации, руб.;

A – величина накопленного купонного дохода, руб.;

C_>1> – размер i-го купона, руб.;

n – количество предстоящих выплат купона, шт.;

t_>i> – число дней до выплаты соответствующего купона;

t – срок до погашения облигаций (в днях). Как правило, t = t_>n>.

1.3Рынок ценных бумаг как часть финансового рынка

Рынок, на котором происходит обмен финансовыми активами, называется финансовым рынком. Финансовые активы, свободно обращающиеся на этом рынке, называются также инструментами финансового рынка, или просто финансовыми инструментами. Важнейшими из них являются ценные бумаги. Рынок ценных бумаг или фондовый рынок – наиболее значительная и мобильная часть финансового рынка в развитых странах.

В рынке ценных бумаг выделяют первичный рынок, на котором происходит размещение вновь выпущенных ценных бумаг. Вторичный рынок связан с дальнейшим обращением ценных бумаг, т.е. с их последующей куплей-продажей.

Существуют две формы организации рынка ценных бумаг: биржевой (централизованный) и внебиржевой (децентрализованный).

На биржевом рынке торговля происходит на фондовых биржах – специальных финансовых торговых центрах. Торговля на биржах ведется по строго установленным правилам и к торговле допущены лишь ценные бумаги, прошедшие процедуру специального отбора – листинга.

Внебиржевой рынок не имеет определенной локализации, его участники связаны коммуникационными сетями, с помощью которых получается необходимая информация, осуществляются и регулируются сделки.

Участниками рынка ценных бумаг являются:

Эмитенты – государство, государственные органы, органы местной администрации, предприятия и другие юридические лица, включая совместные предприятия, инвестиционные фонды, коммерческие банки;

Инвесторы – граждане или юридические лица, приобретающие ценные бумаги от своего имени и за свой счет ;

Инвестиционные институты – в качестве посредника (финансового брокера), инвестиционного консультанта и инвестиционного фонда.

Операции с ценными бумагами проводят фондовые биржи и инвестиционные институты. Фондовая биржа представляет собой организованный и регулярно функционирующий рынок по купле-продаже ценных бумаг. Участниками фондовой биржи являются продавцы, покупатели и посредники (финансовый брокер или маклер, дилер).

Среди участников рынка ценных бумаг очень важная роль принадлежит государству. Государство для финансирования своих нужд выпускает долговые ценные бумаги различного типа от краткосрочных на несколько месяцев до облигаций со сроком погашения 20–30 лет. Государство во многом является органом, регулирующим, контролирующим и направляющим деятельность всех остальных участников рынка.

1.3.1Деятельность коммерческого банка на рынке ценных бумаг

Одним из участников на рынке ценных бумаг выступают коммерческие банки. В зависимости от модели организации фондового рынка роль банков на этом рынке различна. В международной практике различают три модели организации рынка ценных бумаг:

Американская модель организации рынка ценных бумаг характеризуется максимальным ограничением, накладываемым на деятельность коммерческих банков на этом рынке. Основными операторами на фондовом рынке выступают крупные брокерские компании, которые и составляют основную функциональную среду фондового рынка.

Европейская модель, наоборот, исходит из того, что крупнейшими участниками рынка ценных бумаг являются универсальные коммерческие банки. Именно банками непосредственно организуется сам фондовый рынок. Они же формируют деятельность фондовой биржи.

Смешанная модель фондового рынка предполагает присутствие на нем одновременно и банков и небанковских инвестиционных институтов. При этом и те и другие имеют равные права на операции с ценными бумагами.

С момента возрождения современной российской банковской системы (конец 80-х – начало 90-х годов) законодательство придерживалось третьего подхода – универсальности банков.

Российские банки осуществляют непрофессиональные операции с ценными бумагами по общим правилам, действующим для инвесторов и эмитентов, а также в рамках нормативов и по дополнительным правилам, установленным Банком России. При этом Банк России применяет ряд встроенных ограничений на инвестиционные операции банков – повышенные коэффициенты рискованности при расчете коэффициентов соотношения собственных средств банков и различных статей их активов, а также значительные требования к созданию внутренних банковских резервов под потенциальное обесценение вложений в ценные бумаги.

Коммерческие банки могут выполнять одну, несколько или все из рассмотренных ниже основных операций с ценными бумагами.

Эмиссия банком собственных ценных бумаг направлена на привлечение денежных средств для пополнения ресурсов или финансирования инвестиций. Коммерческие банки могут выступать эмитентами не только акций и облигаций, но и инструментов денежного рынка – депозитных сертификатов, векселей, чеков.

Выкуп банком на рынке собственных ранее выпущенных ценных бумаг с возможной последующей перепродажей может преследовать одну или несколько из нижеперечисленных целей:

а) поддержание рыночного курса своих ценных бумаг;

б) выкуп акций для последующей льготной перепродажи сотрудникам и руководству банка;

в) выкуп акций для последующего их погашения;

г) выкуп (отзыв) облигаций для их досрочного погашения;

д) изъятие ценных бумаг у инвесторов для замены другими типами бумаг.

Посредничество банка между эмитентами ценных бумаг и инвесторами заключается в распространении среди инвесторов максимально возможного количества ценных бумаг эмитента. Банки вправе по соглашению с эмитентом организовывать выпуск ценных бумаг и их первичное размещение.

Банки, выступая в качестве инвестиционных компаний, могут выдавать гарантии в пользу других лиц – посредников, занимающихся размещением ценных бумаг, – по размещению ими ценных бумаг эмитента. Такая операция – своего рода страхование рисков. Содержание гарантии сводится к тому, что гарант обязуется принять на себя по обусловленному курсу бумаги, если посредникам не удастся их разместить. Если же размещение состоится, то гарант вправе рассчитывать на комиссионные и вознаграждение за свой риск.

Хранение и учет ценных бумаг по поручению клиентов, а также ценных бумаг, купленных за свой счет, позволяют получить максимальное вознаграждение за точное и быстрое обслуживание клиента.

Управление ценными бумагами предполагает исполнение по поручению клиентов тех функций, которые вытекают из владения ценными бумагами. При предоставлении клиентам услуг, обеспечивающих исполнение их поручений наилучшим образом, банк получает комиссионное вознаграждение.

При купле и продаже ценных бумаг на вторичном рынке за счет и по поручению клиента банк стремится получить вознаграждение от клиентов за точное и быстрое исполнение указаний по покупке или продаже ценных бумаг. Эти посреднические операции банками могут выполнятся в двух вариантах:

• на основании договора комиссии;

• на основании договора поручения.

При покупке и продаже банком ценных бумаг от своего имени и за свой счет достигаются следующие цели:

1. формирование собственного инвестиционного портфеля ценных бумаг. Банк получает доходы от ценных бумаг, находящихся в портфеле, и, поэтому ориентируется на долгосрочные факторы доходности;

2. проведение спекулятивных операций с ценными бумагами. В данном случае банк ориентирован на краткосрочные колебания цен и старается максимизировать разницу между ценой покупки и продажи ценных бумаг;

3. проведение "котировки" определенных ценных бумаг. Банк на основе анализа рынка старается предугадать движение рыночной цены ценных бумаг и назначает цены так, чтобы получить доход на разнице в ценах.

Торговля корпоративными ценными бумагами на фондовой бирже РТС является основным и наиболее сложным бизнес-процессом российского банка, ведущего деятельность на рынке ценных бумаг. Сделка состоит из двух этапов – заключение сделки и ее исполнение. Торговая система обеспечивает выставление котировок. Заключение сделок происходит в ходе телефонных переговоров трейдеров. Заключенные сделки подлежат немедленной (в течение 10 минут) регистрации в торговой системе. В день заключения сделки контрагенту или клиенту направляется подтверждение. Договор купли-продажи как правило должен быть подписан не позднее следующего дня. Исполнение всех обязательств по сделке в любом случае гарантирует член РТС, заключивший сделку. Стандартный договор РТС содержит только существенные условия сделки, все остальные параметры – стандартные правила заключения и исполнения сделок – записаны в Торговом соглашении РТС, что позволяет существенно упростить документооборот и снизить риски. Основными моментами исполнения сделки являются перерегистрация реестродержателем ценных бумаг со счета продавца на счет покупателя или счет номинального держателя, указанного покупателем, и оплата сделки покупателем. НАУФОР (Национальная ассоциация участников фондового рынка) определила стандарты исполнения сделок: 2 дня на оплату, 3 дня на перерегистрацию (7 дней, если реестр не в Москве). После этого при отсутствии штрафных санкций (стандарт – 0,5% за день просрочки) сделка считается закрытой.

Торги по государственным ценным бумагам происходят на ММВБ. По правилам торгов ценные бумаги и денежные средства депонируются заранее. Факт заключения сделки гарантирует, что, во-первых, у продавца депонировано достаточное количество бумаг, а у покупателя – денег, а во-вторых, бумаги и деньги в тот же момент будут переведены соответственно на счета покупателя и продавца в торговой системе ММВБ. Такая организация торговли обеспечивает значительное сокращение рисков по сравнению с торгами в РТС. Кроме того, сделки производятся в одно действие, что существенно упрощает ведение внутреннего учета этих операций, так как по итогам сделки изменения вносятся сразу в портфель, а не в обязательства.

Торговля корпоративными ценными бумагами в фондовой секции ММВБ практически идентична торговле ГКО-ОФЗ: исполнение сделки происходит в момент ее заключения. По сравнению с РТС котировки в фондовой секции ММВБ несколько выше, расходы на перерегистрацию отсутствуют (вернее, уже учтены в ценах), и при практически равной доходности риски при заключении сделок в торговой системе ММВБ существенно ниже.

С целью уменьшения потерь от обесценения ценных бумаг коммерческие банки должны создавать резервы, относящиеся на затраты банка. Банки корректируют эти резервы в первый рабочий день каждого месяца.

Окончательный выбор банком конкретных видов операций с ценными бумагами зависит от типа политики банка на рынке ценных бумаг. Консервативная политика предполагает осуществление отдельных традиционных операций на рынке ценных бумаг, не связанных с повышенными рисками. Умеренная политика направлена на постепенное расширение операций с ценными бумагами, но при этом не проводятся рискованные и спекулятивные операции с ценными бумагами. Агрессивная политика на рынке ценных бумаг выбирается банком в том случае, если он выполняет или стремится выполнять все операции с ценными бумагами. Последний тип политики коммерческого банка на фондовом рынке связан с повышенной рискованностью операций банка в целом, так как риски по операциям с ценными бумагами не отграничены от рисков по кредитно-депозитной и расчетной деятельности.

1.4Модели портфельного инвестирования

О
дним из преимуществ портфельного инвестирования является возможность выбора портфеля для решения специфических инвестиционных задач. Тип портфеля – это его инвестиционная характеристика, основанная на соотношении дохода и риска. При этом важным признаком при классификации типа портфеля является то, каким способом и за счет какого источника данный доход получен: за счет роста курсовой стоимости или за счет текущих выплат – дивидендов, процентов.

Рисунок 1.2 – Классификация портфеля в зависимости от источника дохода

Портфель роста формируется из акций компаний, курсовая стоимость которых растет. Цель данного типа портфеля – рост капитальной стоимости портфеля вместе с получением дивидендов. Однако дивидендные выплаты производятся в небольшом размере. Темпы роста курсовой стоимости совокупности акций, входящей в портфель, определяют виды портфелей, входящие в данную группу.

Портфель агрессивного роста нацелен на максимальный прирост капитала. В состав данного типа портфеля входят акции молодых, быстрорастущих компаний. Инвестиции в данный тип портфеля являются достаточно рискованными, но вместе с тем они могут приносить самый высокий доход.

Портфель консервативного роста является наименее рискованным среди портфелей данной группы. Состоит, в основном, из акций крупных, хорошо известных компаний, характеризующихся хотя и невысокими, но устойчивыми темпами роста курсовой стоимости. Состав портфеля остается стабильным в течение длительного периода времени. Нацелен на сохранение капитала.

Портфель среднего роста представляет собой сочетание инвестиционных свойств портфелей агрессивного и консервативного роста. В данный тип портфеля включаются наряду с надежными ценными бумагами рискованные фондовые инструменты, состав которых периодически обновляется. Данный тип портфеля является наиболее распространенной моделью портфеля и пользуется большой популярностью у инвесторов, не склонных к высокому риску.

Портфель дохода. Данный тип портфеля ориентирован на получение высокого текущего дохода – процентных и дивидендных выплат. Портфель дохода составляется в основном из акций дохода, характеризующихся умеренным ростом курсовой стоимости и высокими дивидендами, облигаций и других ценных бумаг, инвестиционным свойством которых являются высокие текущие выплаты. Особенностью этого типа портфеля является то, что цель его создания – получение соответствующего уровня дохода, величина которого соответствовала бы минимальной степени риска, приемлемого для консервативного инвестора. Поэтому объектами портфельного инвестирования являются высоконадежные инструменты фондового рынка с высоким соотношением стабильно выплачиваемого процента и курсовой стоимости.

Портфель регулярного дохода формируется из высоконадежных ценных бумаг и приносит средний доход при минимальном ровне риска.

Портфель доходных бумаг состоят из высокодоходных облигаций корпораций, ценных бумаг, приносящих высокий доход при среднем уровне риска.

Портфель роста и дохода. Формирование данного типа портфеля осуществляется во избежание возможных потерь на фондовом рынке как от падения курсовой стоимости, так и от низких дивидендных или процентных выплат. Одна часть финансовых активов, входящих в состав данного портфеля, приносит владельцу рост капитальной стоимости, а другая – доход. Потеря одной части может компенсироваться возрастанием другой.

Портфель двойного назначения. В состав данного портфеля включаются бумаги, приносящие его владельцу высокий доход при росте вложенного капитала. В данном случае речь идет о ценных бумагах инвестиционных фондов двойного назначения. Они выпускают собственные акции двух типов, первые приносят высокий доход, вторые – прирост капитала.

Сбалансированный портфель предполагает сбалансированность не только доходов, но и риска, который сопровождает операции с ценными бумагами, и поэтому в определенной пропорции состоит из ценных бумаг с быстрорастущей курсовой стоимостью и из высокодоходных ценных бумаг. Как правило, в состав данного портфеля включаются обыкновенные и привилегированные акции, а также облигации.

Выбор ценных бумаг для портфельного инвестирования зависит от целей инвестора и его отношения к риску. Для всех инвесторов принято выделять три типа целей инвестирования и связанного с ними отношения к риску.

1. Инвестор стремится защитить свои средства от инфляции; для достижения цели он предпочитает вложения с невысокой доходностью, но с низким риском. Этот тип инвестора называют консервативным.

2. Инвестор пытается произвести длительное вложение капитала, обеспечивающее его рост. Для достижения этой цели он готов пойти на рискованные вложения, но в ограниченном объеме, подстраховывая себя вложениями в слабодоходные, но и малорискованные ценные бумаги. Такой тип инвестора называют умеренно-агрессивным.

3. Инвестор стремится к быстрому росту вложенных средств, готов для этого делать вложения в рискованные ценные бумаги, быстро менять структуру своего портфеля, проводя спекулятивную игру на курсах ценных бумаг. Этот тип инвестора принято называть агрессивным.

Если рассматривать типы портфелей в зависимости от степени риска, который приемлет инвестор, то результаты можно свести в таблицу 1.2.

Таблица 1.2 – Связь между типом инвестора и типом портфеля

Тип инвестора	Цель инвестирования	Степень риска	Тип ценной бумаги	Тип портфеля
Консерва-тивный	Защита от инфляции	Низкая	Государственные ценные бумаги, акции и облигации крупных стабильных эмитентов	Высоконадежный, но низко доходный
Умеренно-агрессив-ный	Длительное вложение капитала и его рост	Средняя	Малая доля государственных ценных бумаг, большая доля ценных бумаг крупных и средних, но надежных эмитентов с тигельной рыночной историей	Диверсифи-цированный
Агрессив-ный	Спекулятивная игра, возможность быстрого роста итоженных средств	Высокая	Высокая доля высокодоходных ценных бумаг небольших эмитентов, венчурных компаний и т.д.	Рискованный, но высоко-доходный

Рассматривая вопрос с точки зрения практики отечественного фондового рынка, необходимо, прежде всего, решить проблему: а имеется ли на нем достаточное количество качественных ценных бумаг, инвестируя в которые можно достигнуть вышеприведенных норм. В частности, на отечественном фондовом рынке разновидностей портфелей не так уж и многою.

1.5Структура инвестиционного процесса

Инвестиционный процесс представляет собой принятие инвестором решения относительно ценных бумаг, в которые осуществляются инвестиции, объемов и сроков инвестирования. Следующая процедура, включающая пять этапов, составляет основу инвестиционного процесса:

1. Выбор инвестиционной политики.

2. Анализ рынка ценных бумаг.

3. Формирование портфеля ценных бумаг.

4. Пересмотр портфеля ценных бумаг.

5. Оценка эффективности портфеля ценных бумаг.

Первый этап – выбор инвестиционной политики – включает определение цели инвестора и объема инвестируемых средств. Цели инвестирования должны формулироваться с учетом как доходности так и риска.

Необходимо оценить имеющиеся свободные ресурсы, которые должны играть роль инвестиционного капитала, необходимо собрать достаточную информацию о доступных инвестиционных средствах, оценить предварительно экономическую конъюнктуру и прогнозы на будущее и т. п. На этом этапе инвестор с той или иной степенью точности определяет свой инвестиционный горизонт, т.е. промежуток времени, на который распространяется его стратегия и по отношению к которому оцениваются результаты инвестиционного процесса. Величина временного горизонта определяется как целями инвестора, так и его способностью прогнозировать будущее положение дел.

Разработка инвестиционной стратегии всегда основывается на анализе доходности от вложения средств, времени инвестирования и возникающих при этом рисков. Эти факторы во взаимосвязи определяют эффективность вложений в тот или иной инструмент фондового рынка. Принятая инвестиционная стратегия определяет тактику вложения средств: сколько средств и в какие ценные бумаги следует инвестировать и, следовательно, всегда является основой операций с ценными бумагами. Эффективность инвестирования различается в зависимости от того, используются ли для вложений только собственные средства или привлекаются и заемные ресурсы.

Этот этап инвестиционного процесса завершается выбором потенциальных видов финансовых активов для включения в основной портфель. Так, на современном рынке ценных бумаг имеются десятки тысяч различных облигаций и акций, о большинстве которых средний инвестор обычно ничего не знает. Даже профессионалы финансового рынка ограничивают свой круг внимания не слишком большим числом бумаг, о которых они имеют достаточно информации, за поведением которых они тщательно следят. Первичный отбор основывается на финансовом положении инвестора, на его осведомленности о тех или иных бумагах, о различных аспектах налогообложения, связанного с ценными бумагами, недвижимостью, на доступности и легкости реализации операции с этими активами и т. п. Сделав такой отбор, инвестор сужает все многообразие инвестиционного рынка до обозримого множества инвестиционных активов, которые он может оценивать, сравнивать и с которыми он реально может осуществлять сделки.

Второй этап инвестиционного процесса, известный как анализ ценных бумаг, включает изучение отдельных видов ценных бумаг (или групп бумаг) в рамках основных категорий, указанных выше. Одной из целей такого исследования является определение тех ценных бумаг, которые представляются неверно оцененными в настоящий момент. Существует много различных подходов к анализу ценных бумаг.

Традиционный анализ ценных бумаг обычно предусматривает подход "сверху вниз", начинающийся с экономического анализа, а затем переходящий к анализу состояния отрасли и, наконец, к фундаментальному анализу.

Экономический анализ направлен на оценку общего состояния экономики и ее потенциального воздействия на доходы, получаемые по ценным бумагам. Как правило, при стабильной экономике курсу акций свойственна тенденция роста, а при нарушении стабильности экономики курсы акций падают. Несомненно, что эта взаимосвязь не является совершенной, но она тем не менее сильна.

Отраслевой анализ связан с отраслью экономики, в рамках которой функционирует конкретная компания, а также с перспективами данной отрасли.

Технический анализ в простейшей его форме включает изучение конъюнктуры курсов рынка акций, с тем чтобы дать прогноз динамики курсов акций конкретной фирмы. Инструменты для проведения технического анализа – графики. Они наглядно отражают итоговую картину движения рынка и курсов отдельных выпусков. Информация о движении цен представлена графиком (кривой), в котором аналитик пытается найти устойчивые, повторяющиеся конфигурации. Основные типы таких конфигураций (типов поведения) классифицируются, и в текущей информации о ценах пытаются обнаружить одну из них. Если это удается, то будущее поведение цен предсказывается на основе такой конфигурации.

Альтернативный способ изучения рынка построен на использовании разных видов статистических данных. Следовательно, технический анализ – это анализ данных во времени; для него необходимо иметь информацию за какой либо промежуток времени, чтобы проанализировать ее техническими методами.

Первоначально проводится исследование курсов за прошедший период с целью выявления повторяющихся тенденций или циклов в динамики курсов. Затем анализируются курсы акций за последний период времени, с тем чтобы выявить текущие тенденции, аналогичным обнаруженным ранее. Это сопоставление существующих тенденций с прошлыми осуществляется, исходя из предположения, что ценовые тренды периодически повторяются. Таким образом, выявляя текущие тенденции, аналитик надеется дать достаточно точный прогноз будущей динамики курсов рассматриваемый акций.

Обычно техническим анализом акций занимаются до более глубокого фундаментального анализа. Если с точки зрения технического анализа данный выпуск акций кажется интересным, тогда они продолжают его изучение средствами фундаментального анализа. Если же с точки зрения технического анализа выпуск не представляет интереса, их внимание переключается на другие акции.

Фундаментальный анализ предусматривает глубинное изучение финансового положения конкретной компании и вытекающего из него поведения ее ценных бумаг. При этом информация извлекается прежде всего из изучения финансовых отчетов корпорации за текущий и прошлые годы. Положение компании сравнивается с аналогичными компаниями в отрасли с помощью так называемых коэффициентов эффективности: показателей, вычисляемых по данным баланса и других финансовых отчетов. Эти коэффициенты характеризуют различные относительные характеристики эффективности деятельности предприятия (коэффициент ликвидности, коэффициент финансового рычага, прибыли на акцию и др.). Но основной целью фундаментального анализа является прогноз величины будущих прибылей компании и связанных с ними дивидендов и роста балансовой стоимости акции. Последняя является отношением текущей рыночной стоимости собственного капитала компании к числу всех выпущенных акций.

Фундаментальный анализ исходит из того, что «истинная» (или внутренняя) стоимость любого финансового актива равна приведенной стоимости всех наличных денежных потоков, которые владелец актива рассчитывает получить в будущем. В соответствии с этим аналитик стремится определить время поступления и величину этих наличных денежных потоков, а затем рассчитывает их приведенную стоимость. После того, как внутренняя стоимость акции данной фирмы определена, она сравнивается с текущим рыночным курсом акций с целью выяснить, правильно ли оценена акций на рынке. Акции, внутренняя стоимость которых меньше текущего рыночного курса, называются переоцененными, а те акции, рыночный курс которых ниже внутренне стоимости, – недооцененными. Разница между внутренней стоимостью и текущим рыночным курсом также представляет собой важную информацию, т.к. обоснованность заключения аналитика о неправильности оценки данной акции зависит в значительной степени от этой величины. Считается, что любые случаи существенно неверной оценки исправляются впоследствии рынком: курсы недооцененных акций растут быстрее, а переоцененных – медленнее, чем средние рыночные курсы.

И фундаментальный, и технический анализы имеют множество горячих сторонников и не менее убежденных противников. Оба эти подхода имеют долгую практику (на Западе) и представляют собой два традиционных метода инвестиционного анализа.

Третий этап инвестиционного процесса – формирование портфеля ценных бумаг – включает определение конкретных активов для вложения средств а также пропорций распределения инвестируемого капитала между активами. При этом инвестор сталкивается с проблемами селективности, выбора времени операций и диверсификации. Селективность, называемая также микропрогнозированием относится к анализу ценных бумаг и связана с прогнозированием динамики цен отдельных видов бумаг. Выбор времени операций, или макропрогнозирование, включает прогнозирование изменения уровня цен на акции по сравнению с ценами для фондовых инструментов с фиксированным доходом, такими, как корпоративные облигации. Диверсификация заключается в формировании инвестиционного порфеля таким образом, чтобы при определенных ограничениях минимизировать риск.

Четвертый этап инвестиционного процесса – пересмотр портфеля – связан с периодическим повторение трех предыдущих этапов. То есть через некоторое время цели инвестирования могут измениться, в результате чего текущий портфель перестанет быть оптимальным. Другим основанием для пересмотра портфеля является изменение курса ценных бумаг с течением времени. Решение о пересмотре портфеля зависит помимо прочих факторов от размера трансакционных издержек и ожидаемого роста доходности пересмотренного портфеля. Лица, профессионально занимающиеся инвестициями в ценные бумаги, часто проводят различие между пассивным и активным управлением.

Основополагающий принцип в инвестировании с пассивным управлением можно сформулировать так: «купил и храни». Однако его реализация предполагает формирование широко диверсифицируемого портфеля. Однако, если рыночные изменения приводят к неадекватности его инвестиционным целям, состав портфеля изменяется. Для обеспечения своевременной ревизии осуществляется мониторинг фондового рынка. Пассивное управление портфелем требует издержек: снижение риска сопровождается увеличением затрат на его сокращение и поэтому данная инвестиционная стратегия применяется банковскими и крупными корпоративными инвесторами.

Портфельное инвестирование с активным управлением основано на постоянном пере структурировании портфеля в пользу наиболее доходных в данный момент ценных бумаг. Схема наиболее сложна, так как требует не только большой аналитической работы на основе постоянно получаемой и обрабатываемой информации с биржи, но и дорогостоящих технических систем и технологий, обеспечивающих поступление и обработку информации с рынка в режиме реального времени. Активное управление – самый затратный вариант инвестирования, и для инвестора возможность активного управления портфелем существенно ограничивается комиссионными, взимаемыми дилерами. Поэтому эту схему, как правило, используют крупные инвестиционные компании, банки-дилеры и другие профессионалы, располагающие специальными аналитическими отделами и достаточными средствами.

Пятый этап инвестиционного процесса – оценка эффективности портфеля – включает периодическую оценку как полученной доходности, так и показателей риска, с которыми сталкивается инвестор. При этом необходимо использовать приемлемые показатели доходности и риска, а также соответствующие стандарты («эталонные» значения) для сравнения.

2Методики формирования оптимальной структуры портфеля

На практике используют множество методик формирования оптимальной структуры портфеля ценных бумаг. Большинство из них основано на методике Марковица. Он впервые предложил математическую формализацию задачи нахождения оптимальной структуры портфеля ценных бумаг в 1951 году, за что позднее был удостоен Нобелевской по экономике.

Основными постулатами, на которых построена классическая портфельная теория, являются следующие:

1. Рынок состоит из конечного числа активов, доходности которых для заданного периода считаются случайными величинами.

2. Инвестор в состоянии, например, исходя из статистических данных, получить оценку ожидаемых (средних) значений доходностей и их попарных ковариаций и степеней возможности диверсификации риска.

3. Инвестор может формировать любые допустимые (для данной модели) портфели. Доходности портфелей являются также случайными величинами.

4. Сравнение выбираемых портфелей основывается только на двух критериях – средней доходности и риске.

5. Инвестор не склонен к риску в том смысле, что из двух портфелей с одинаковой доходностью он обязательно предпочтет портфель с меньшим риском.

Рассмотрим подробнее сформировавшиеся на данный момент портфельные теории, некоторые из которых будут применены далее при проведении практического расчета оптимального портфеля ценных бумаг.

2.1Модель Марковица

Основная идея модели Марковица заключается в том, чтобы статистически рассматривать будущий доход, приносимый финансовым инструментом, как случайную переменную то есть доходы по отдельным инвестиционным объектам случайно изменяются в некоторых пределах. Тогда, если неким образом случайно определить по каждому инвестиционному объекту вполне определенные вероятности наступления, можно получить распределение вероятностей получения дохода по каждой альтернативе вложения средств. Это получило название вероятностной модели рынка. Для упрощения модель Марковица полагает, что доходы распределены нормально.

По модели Марковица определяются показатели, характеризующие объем инвестиций и риск что позволяет сравнивать между собой различные альтернативы вложения капитала с точки зрения поставленных целей и тем самым создать масштаб для оценки различных комбинаций.

В качестве масштаба ожидаемого дохода из ряда возможных доходов на практике используют наиболее вероятное значение, которое в случае нормального распределения совпадает с математическим ожиданием.

Математическое ожидание дохода по i-й ценной бумаге (m_>i>) рассчитывается следующим образом:

, (12)

где R_>i> – возможный доход по i-й ценной бумаге, руб.;

P_>ij> – вероятность получение дохода;

n – количество ценных бумаг.

Для измерения риска служат показатели рассеивания, поэтому чем больше разброс величин возможных доходов, тем больше опасность, что ожидаемый доход не будет получен. Мерой рассеивания является среднеквадратическое отклонение:

_> >. (13)

В отличии от вероятностной модели, параметрическая модель допускает эффективную статистическую оценку. Параметры этой модели можно оценить исходя из имеющихся статистических данных за прошлые периоды. Эти статистические данные представляют собой ряды доходностей за последовательные периоды в прошлом.

Любой портфель ценных бумаг характеризуется двумя величинами: ожидаемой доходностью

_> >, (14)

где X_>i> – доля общего вложения, приходящаяся на i-ю ценную бумагу;

m_>i> – ожидаемая доходность i-й ценной бумаги, %;

m_>p> – ожидаемая доходность портфеля, %

и мерой риска – среднеквадратическим отклонением доходности от ожидаемого значения

_> > (15)

где _>p> – мера риска портфеля;

_>ij>_> >– ковариация между доходностями i-й и j-й ценных бумаг;

X_>i> и X_>j> – доли общего вложения, приходящиеся на i-ю и j-ю ценные бумаги;

n – число ценных бумаг портфеля.

Ковариация доходностей ценных бумаг (_>ij>) равна корреляции между ними, умноженной на произведение их стандартных отклонений:

_> > (16)

где _>ij> – коэффициент корреляции доходностей i-ой и j-ой ценными бумагами;

_>i>, _>j> – стандартные отклонения доходностей i-ой и j-ой ценных бумаг.

Для i = j ковариация равна дисперсии акции.

Рассматривая теоретически предельный случай, при котором в портфель можно включать бесконечное количество ценных бумаг, дисперсия (мера риска портфеля) асимптотически будет приближаться к среднему значению ковариации.

Графическое представление этого факта представлено на рисунке 2.1.

Р
исунок 2.1 – Риск портфеля и диверсификация

Совокупный риск портфеля можно разложить на две составные части: рыночный риск, который нельзя исключить и которому подвержены все ценные бумаги практически в равной степени, и собственный риск, который можно избежать при помощи диверсификации. При этом сумма вложенных средств по всем объектам должна быть равна общему объему инвестиционных вложений, т.е. сумма относительных долей в общем объеме должна равняться единице.

Проблема заключается в численном определении относительных долей акций и облигаций в портфеле, которые наиболее выгодны для владельца. Марковиц ограничивает решение модели тем, что из всего множества «допустимых» портфелей, т.е. удовлетворяющих ограничениям, необходимо выделить те, которые рискованнее, чем другие. При помощи разработанного Марковицем метода критических линий можно выделить неперспективные портфели. Тем самым остаются только эффективные портфели.

Отобранные таким образом портфели объединяют в список, содержащий сведения о процентом составе портфеля из отдельных ценных бумаг, а также о доходе и риске портфелей.

Объяснение того факта, что инвестор должен рассмотреть только подмножество возможных портфелей, содержится в следующей теореме об эффективном множестве: «Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых обеспечивает максимальную ожидаемую доходность для некоторого уровня риска и минимальный риск для некоторого значения ожидаемой доходности». Набор портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством.

На рисунке 2.2 представлены недопустимые, допустимые и эффективные портфели, а также линия эффективного множества.

Р
исунок 2.2 – Допустимое и эффективное множества

В модели Марковица допустимыми являются только стандартные портфели (без коротких позиций). Использую более техническую терминологию, можно сказать, что инвестор по каждому активу находится в длинной позицияи. Длинная позиция – это обычно покупка актива с намерением его последующей продажи (закрытие позиции). Такая покупка обычно осуществляется при ожидании повышения цены актива в надежде получить доход от разности цен покупки и продажи.

Из-за недопустимости коротких позиций в модели Марковица на доли ценных бумаг в портфели накладывается условие неотрицательности. Поэтому особенностью этой модели является ограниченность доходности допустимых портфелей, т.к. доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен.

Для выбора наиболее приемлемого для инвестора портфеля ценных бумаг можно использовать кривые безразличия. В данном случае эти кривые отражают предпочтение инвестора в графической форме. Предположения, сделанные относительно предпочтений, гарантируют, что инвесторы могут указать на предпочтение, отдаваемое одной из альтернатив или на отсутствие различий между ними.

Если же рассматривать отношение инвестора к риску и доходности в графической форме, откладывая по горизонтальной оси риск, мерой которого является среднеквадратическое отклонение (_>p>), а по вертикальной оси – вознаграждение, мерой которого является ожидаемая доходность (r_>p>), то можно получить семейство кривых безразличия.

Располагая информацией об ожидаемой доходности и стандартных отклонениях возможных портфелей ценных бумаг, можно построить карту кривых безразличия, отражающих предпочтения инвесторов. Карта кривых безразличия – это способ описания предпочтений инвестора к возможному риску полностью или частично потерять вкладываемые в портфель ценных бумаг деньги или получить максимальны доход.

Различные позиции инвесторов по отношению к риску можно представить в виде карт кривых, отражающих полезность вложений в те или иные инвестиционные портфели (рисунок 2.3). Каждая из указанных на рисунке 2.3 позиций инвестора к риску характерна тем, что любое уменьшение им риска сказывается на сокращении доходности и стандартном отклонении каждого из портфелей. И поскольку портфеля включает в себя набор различных бумаг, то вполне объяснимым является зависимость его от ожидаемой доходности и стандартного отклонения его от ожидаемой доходности и стандартного отклонения каждой ценной бумаги, входящей в портфель.

Р
исунок 2.3 – Карты кривых безразличия инвесторов

Инвестор должен выбирать портфель, лежащий на кривой безразличия, расположенной выше и левее всех остальных кривых. В теореме об эффективном множестве утверждается, что инвестор не должен рассматривать портфели, которые не лежат на левой верхней границе множества достижимости, что является ее логическим следствием. Исходя из этого, оптимальный портфель находится в точке касания одной из кривых безразличия самого эффективного множества. На рисунке 2.4 оптимальный портфель для некоторого инвестора обозначен O^*.

О
пределение кривой безразличия клиента является нелегкой задачей. На практике ее часто получают в косвенной или приближенной форме путем оценки уровня толерантности риска, определяемой как наибольший риск, который инвестор готов принять для данного увеличения ожидаемой доходности.

Поэтому, с точки зрения методологии модель Марковица можно определить как практически-нормативную, что не означает навязывания инвестору определенного стиля поведения на рынке ценных бумаг. Задача модели заключается в том, чтобы показать, как поставленные цели достижимы на практике.

2.2Модель Блека

Модель Блека аналогична модели Марковица, но в отличии от последней в ней отсутствует условие неотрицательности на доли активов портфеля. Это означает, что инвестор может совершать короткие продажи, т.е. продавать активы, предоставленные ему в виде займа. В этом случае инвестор рассчитывает на снижение курса ценной бумаги и планирует вернуть заем теми же ценными бумагами, но приобретенными по более низкому курсу.

В следствии отсутствия ограничений на доли активов в портфеле потенциальная прибыль инвестора не ограничена максимальной доходностью одного из активов, входящих в портфель.

2.3Индексная модель Шарпа

Как следует из модели Марковица, задавать распределение доходов отдельных ценных бумаг не требуется. Достаточно определить только величины, характеризующие это распределение: математическое ожидание, среднеквадратическое отклонение и ковариацию между доходностями отдельных ценных бумаг. На практике для сравнительно небольшого числа ценных бумаг произвести такие расчеты по определению ожидаемого дохода и дисперсии возможно. При определении же коэффициента корреляции трудоемкость весьма велика.

В 1960-х годах Уильям Шарп первым провел регрессионный анализ рынка акций США. Для избежания высокой трудоемкости Шарп предложил индексную модель. Причем он не разработал нового метода составления портфеля, а упростил проблему таким образом, что приближенное решение может быть найдено со значительно меньшими усилиями. Шарп ввел -фактор, который играет особую роль в современной теории портфеля.

, (17)

где _>iM> – ковариация между темпами роста курса ценной бумаги и темпами роста рынка;

²_>M> – дисперсия доходности рынка.

Показатель «бета» характеризует степень риска бумаги и показывает, во сколько раз изменение цены бумаги превышает изменение рынка в целом. Если бета больше единицы, то данную бумагу можно отнести к инструментам с повышенной степенью риска, т.к. ее цена движется в среднем быстрее рынка. Если бета меньше единицы, то степень риска этой бумаги относительно низкая, поскольку в течение периода глубины расчета ее цена изменялась медленнее, чем рынок. Если бета меньше нуля, то в среднем движение этой бумаги было противоположно движению рынка в течение периода глубины расчета.

В индексной модели Шарпа используется тесная корреляция между изменением курсов отдельных акций. Предполагается, что необходимые входные данные можно приблизительно определить при помощи всего лишь одного базисного фактора и отношений, связывающих его с изменением курсов отдельных акций. Как правило за такой фактор берется значение какого-либо индекса. Зависимость доходности ценной бумаги от индекса описывается следующей формулой:

, (18)

где r_>i> – доходность ценной бумаги i за данный период;

r_>I> – доходность на рыночный индекс I за этот же период;

_>iI> – коэффициент смещения;

_> >_>iI> – коэффициент наклона;

_> >_>iI> – случайная погрешность.

Как следует из уравнения, «бету» ценной бумаги можно интерпретировать как наклон линии. Если этот коэффициент был постоянным от периода к периоду, то «историческую бету» бумаги можно оценить путем сопоставления прошлых данных о соотношении доходности рассматриваемой бумаги и доходности рынка (индекса). Статистическая процедура для получения таких апостериорных значений коэффициента «бета» представляет собой простую линейную регрессию, или метод наименьших квадратов.

Уравнение (18), записанное без случайной погрешности, является уравнением линейной регрессии. Параметр «бета» поэтому является коэффициентом регрессии и может быть определен по формуле:

, (19)

где x_>i> – доходность рынка в i-й период времени;

y_>i> – доходность рынка в i-й период времени;

n – количество периодов.

По Шарпу показатель «альфа» (его также называют сдвигом) определяет составляющую доходности бумаги, которая не зависит от движения рынка.

. (20)

В соответствие с одной из точек зрения, «альфа» является своего рода мерой недо- или переоценки рынком данной бумаги. Положительная «альфа» свидетельствует о переоценке рынком данной бумаги. Отрицательная «альфа» свидетельствует о недооценке рынком данной бумаги.

Случайная погрешность  показывает, что индексная модель Шарпа не очень точно объясняет доходности ценной бумаги. Разность между действительным и ожидаемым значениями при известной доходности рыночного индекса приписывается случайной погрешности.

Случайную погрешность можно рассматривать как случайную переменную, которая имеет распределение вероятностей с нулевым математическим ожиданием и стандартным отклонением, вычисляемым по формуле:

. (21)

Истинное значение коэффициента «бета» ценной бумаги невозможно установить, можно лишь оценить это значение. Так что даже если бы истинное значение «беты» оставалось постоянным всегда, его оценка, полученная по методу наименьших квадратов, все равно бы менялась бы во времени из-за ошибок при оценке – ошибок выборки. Стандартная ошибка «беты» есть попытка оценить величину таких ошибок:

. (22)

Аналогично стандартная ошибка для «альфы» дает оценку величины отклонения прогнозируемого значения от «истинного»:

. (23)

Для характеристики конкретной ценной бумаги используются и другие параметры. R-squared (R²), или коэффициент детерминации, равен квадрату коэффициента корреляции цены бумаги и рынка. R-squared меняется от нуля до единицы и определяет степень согласованности движения рынка и бумаги.

. (24)

Коэффициент детерминации представляет собой пропорцию, в которой изменение доходности ценной бумаги связано с изменением доходности рыночного индекса. Другими словами, он показывает, в какой степени колебания доходности ценной бумаги можно отнести за счет колебаний доходности рыночного индекса.

Если этот коэффициент равен единице, то бумага полностью коррелирует с рынком, если равен нулю, то движение рынка и бумаги абсолютно независимы.

Ошибки показателей «бета» и «альфа» определяются непосредственно ошибкой регрессионной модели. Естественно, в первую очередь они зависят от глубины расчета.

При различных стадиях рынка (растущий, падающий) для достижения лучшего эффекта можно пользоваться следующими комбинациями коэффициентов:

Таблица 2.1 – Комбинации коэффициентов регрессионного анализа

	На покупку	На продажу
Падающий рынок
Растущий рынок

На западных рынках значения , , R² регулярно рассчитываются для всех ценных бумаг и публикуются вместе с индексами. Пользуясь этой информацией, инвестор может сформировать собственный портфель ценных бумаг. На российском рынке профессионалы постепенно тоже начинают использовать -, -, R²-анализ.

2.4Модель Тобина с безрисковым активом

В отличии от моделей Марковица и Блека, которые связаны с выбором класса допустимых портфелей, модель Тобина в большей степени относится к структуре рынка, нежели к структуре допустимых портфелей. В этой модели предполагается существование безрискового актива, доходность которого не зависит от состояния рынка и всегда имеет одно и то же значение. Поскольку неопределенность конечной стоимости безрискового актива отсутствует, то стандартное отклонение для этого актива равно нулю. Это означает, что корреляция между ставкой доходности по безрисковому активу и ставкой доходности по любому рисковому активу равна нулю.

Дж. Тобин показал, что если  = (p_>i>, …, p_>n>) – некоторый портфель (p_>i> – доля i-го актива в портфеле), а f – безрисковый актив, то все портфели вида

(25)

л
ежат на прямой, проходящей через точки (0, r_>f>) и (_>p>, r_>p>), где r_>f> и r_>p>_> >– безрисковая и рисковая доходности соответственно. Среди всех таких прямых нужно выбрать самую крутую (более крутая дает большую доходность при заданном риске), т.е. ту, которая проходит через точку (0, r_>p>) и точку касания T к эффективной границе (рисунок 2.5).

Рисунок 2.5 – Достижимое и эффективное множества при возможности безрискового кредитования.

Множество достижимости существенно изменяется в результате рассмотрения безрискового кредитования. Две границы являются прямыми линиями, выходящими из точки, соответствующей безрисковому активу Нижняя линия соединяет две точки, соответствующие безрисковому активу и портфелю с набольшим риском и доходностью. Поэтому она представляет портфели, являющееся комбинациями этого портфеля и безрискового актива.

Другая прямая линия, выходящая из точки, соответствующей безрисковому активу, представляет комбинации безрискового актива и определенного рискованного портфеля из эффективного множества модели Марковица. Эта линия является касательной к данному эффективному множеству (в точке, обозначенной T).

Хотя и другие рискованные эффективные портфели из модели Марковица могут быть скомбинированы с безрисковым активом, портфель T заслуживает особого внимания. Потому что не существует портфеля, состоящего из рискованных ценных бумаг, который, будучи соединен прямой линией с точкой, соответствующей безрисковому активу, лежал бы левее и выше его. Другими словами, из всех линий, которые могут быть проведены из точки, соответствующей безрисковому активу, и соединяют эту точку с рискованным активом или рискованным портфелем, ни одна не имеет больший наклон, чем линия, идущая в точку Т.

Это важно потому, что часть эффективного множества модели Марковица отсекается этой линией. В частности, портфели, которые принадлежали эффективному множеству в модели Марковица и располагались между минимально рискованным портфелем, обозначенным через V, и портфелем Т, с введением возможности инвестирования в безрисковые активы не являются эффективными. Теперь эффективное множество состоит из прямого и искривленного отрезка. Прямой отрезок идет от безрискового актива в точку Т и поэтому представляет портфели, составленные из различных комбинаций безрискового актива и портфеля Т. Искривленный отрезок расположен выше и правее точки T представляет портфели из эффективного множества модели Марковица.

Анализ может быть расширен за счет введения возможности заимствования. Это означает, что теперь инвестор не ограничен своим начальным капиталом при принятии решения о том, сколько денег инвестировать в рискованные активы. Однако если инвестор занимает деньги, то он должен платить процент по займу. Если процентная ставка известна и неопределенность с выплатой займа отсутствует, то это часто называется безрисковым заимствованием.

Предполагается, что процентная ставка по займу равна ставке, которая может быть заработана инвестированием в безрисковые активы.

Рисунок 2.6 изображает, как изменяется допустимое множество, если введена возможность как предоставления, так и получения займа по одной и той же безрисковой процентной ставке. Множество достижимости представлено областью, расположенной между двумя лучами, выходящими из точки, соответствующей безрисковой ставке, и проходящими через точки, соответствующие наиболее доходному портфелю и портфелю, обозначенному через Т. Эти два луча уходят в бесконечность при условии, что нет ограничений на величину получаемого займа.

Р
исунок 2.6 – Достижимое и эффективное множества в случае возможности безрискового заимствования и кредитования.

Луч, идущий через портфель Т, является особенно важным, поскольку он представляет эффективное множество. Как и прежде, линия, идущая через T, является касательной к эффективному множеству модели Марковица. Кроме портфеля T ни один из портфелей, которые находились в эффективном множестве модели Марковица, не является эффективным после введения возможности предоставления и получения безрисковых займов.

В модели оценки финансовых активов новую эффективную границу, полученную с учетом безрискового актив, называют рыночной линией (Capital Market Line, CML), а портфель Т – рыночным портфелем.

2.4.1Алгоритм Элтона-Грубера-Падберга

При определении структуры касательного портфеля Т в модели с безрисковым активом можно также воспользоваться методом критических линий, как и в модели Марковица. Но имеется и другой метод определения структуры этого портфеля, который не требует определения «угловых» портфелей и, следовательно, является более простым.

Предполагается, что доходности ценной бумаги могут быть описаны рыночной моделью (индексной моделью Шарпа), а также, что существует возможность безрискового заимствования и кредитования по ставке r_>f>. Метод разработан Элтоном, Грубером и Падбергом.

Алгоритм начинается с замечания, что наклон линии, выходящей из точки r_>f> и проходящей через любой конкретный портфель равен:

. (26)

«Касательный» портфель Т определяется как имеющий максимальную тхэту (). Для поиска портфеля, имеющего максимальную , применяется следующий пятишаговый алгоритм:

1. Упорядочить ценные бумаги в порядке убывания отношений доходности к систематическому риску (reward-to-volatility ratio):

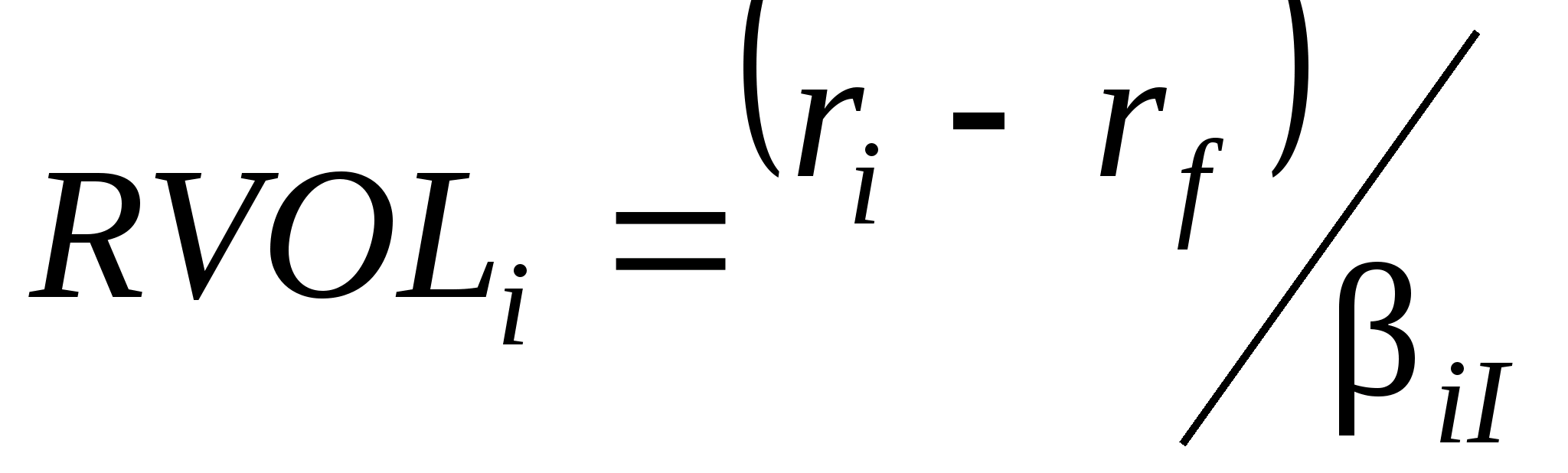, (27)

где r_>i> – ожидаемая доходность i-й ценной бумаги;

r_>f> – безрисковая ставка;

_>iI> – коэффициент «бета».

Числитель этого выражения представляет собой ожидаемое «вознаграждение» за приобретение ценной бумаги, а знаменателем является соответствующий ей -коэффициент. Это отношение иногда называют отношением Трейнора.

2. Начиная с ценной бумаги, имеющей наибольшее RVOL_>i>, добавлять ценные бумаги одну за другой и вычислять _>i>:

, (28)

где ²_>I> – систематический риск – дисперсия рыночного индекса;

²_>>_>I> – несистематический риск – дисперсия случайной ошибки.

3. Сравнивать величины _>i> с соответствующими RVOL_>i> до тех пор, пока _>i> меньше RVOL_>i>. С некоторого момента это соотношение изменится на противоположное. Пусть k – максимальный номер, для которого это соотношение еще не выполнено. Тогда ценные бумаги с 1 по k будут иметь не нулевые веса в портфеле Т, а остальные – нулевые. Таким образом, _>k> является «ставкой отсечения» для RVOL.

4. Вычислить величины Z_>i>, чтобы определить, с какими весами будут входить в портфель первые k ценных бумаг:

. (29)

Значения Z_>i> для i = k + 1, ..., N полагаются равными нулю.

5. Разделить каждую Z_>i> на сумму Z_>i> для получения весов для ценной бумаги:

(30)

Это сделать необходимо, так как сумма Z_>i> обычно не равна единиц.

Полученные значения X_>i> и являются долями ценных бумаг в портфеле Т.

2.5Модель оценки финансовых активов

Некоторые из предположений, на которых основывается модель оценки финансовых активов (Capital Asset Prising Model, CAPM), совпадают с предположениями нормативного подхода к инвестированию, описанного в предыдущих разделах. Эти предположения дополняются следующими:

1. Для всех инвесторов период вложения одинаков.

2. Безрисковая процентная ставка одинакова для всех инвесторов.

3. Информация свободно и незамедлительно доступна для всех инвесторов.

4. Инвесторы имеют однородные ожидания, т.е. они одинаково оценивают ожидаемые доходности, среднеквадратичные отклонения и ковариации доходностей ценных бумаг.

Как вытекает из этих предположений, в модели оценки финансовых активов рассматривается предельный случай. Все инвесторы обладают одной и той же информацией и по-одинаковому оценивают перспективы ценных бумаг. Неявно это означает, что они одинаковым образом анализируют получаемую информацию. Рынки ценных бумаг являются совершенными рынками в том смысле, что в них нет факторов, которые бы препятствовали инвестициям. Это позволяет сместить фокус рассмотрения с того, как следует инвестору размещать свои средства, на то, что произойдет с курсами ценных бумаг, если все инвесторы будут поступать одинаково. Исследуя коллективное поведение всех инвесторов на рынке, можно выявить характер конечной равновесной зависимости между риском и доходностью каждой ценной бумаги.

Сначала инвесторы анализируют ценные бумаги и определяют структуру «касательного» портфеля. В итоге, в равновесном случае все инвесторы выбирают один и тот же «касательный» портфель, т.к. оценки инвесторов относительно ожидаемых доходностей бумаг, их дисперсий и ковариаций, а также величины безрисковой процентной ставки полностью совпадают. К тому же линейное эффективное множество является одним и тем же для всех инвесторов, так как оно состоит из комбинаций согласованного «касательного» портфеля и безрискового заимствования или кредитования.

В связи с тем что все инвесторы имеют одно и то же эффективное множество, единственной причиной, по которой они предпочтут различные портфели, является то, что они характеризуются различными кривыми безразличия. Хотя выбранные портфели будут различными, каждый инвестор выберет одну и ту же комбинацию рискованных бумаг, обозначенных на рисунке 2.5 через Т. Это означает, что каждый инвестор распределит свои средства среди рискованных бумаг в одной и той же относительной пропорции, увеличивая безрисковое заимствование или кредитование с целью достижения предпочтительной для него комбинации риска и дохода. Это свойство модели оценки финансовых активов часто называют теоремой разделения: «Оптимальная для инвестора комбинация активов не зависит от его предпочтения относительно риска и дохода».

Другими словами, оптимальная комбинация рискованных активов может быть определена без построения кривых безразличия каждого инвестора.

Объяснением теоремы разделения служит то, что все портфели, расположенные на линейном эффективном множестве, включают в себя инвестирование в «касательный» портфель в сочетании с различным уровнем безрискового заимствования или кредитования. В модели оценки финансовых активов каждый инвестор сталкивается с одним и тем же линейным эффективным множеством. Это означает, что все будут инвестировать в один и тот же «касательный» портфель (в сочетании с определенным объемом безрискового заимствования и кредитования, который определяется кривой безразличия каждого инвестора). Из этого следует, что доля рискованных ценных бумаг в портфеле каждого инвестора будет одной и той же.

Другим важным свойством модели оценки финансовых активов является то, что в состоянии равновесия каждый вид ценных бумаг имеет ненулевую долю в «касательном» портфеле. Основанием этого свойства является теорема разделения, которая утверждает, что доля рискованных активов в портфеле каждого инвестора не зависит от предпочтения инвестора относительно риска и доходности. Эта теорема основывается на том, что рискованная доля портфеля каждого инвестора представляет собой просто инвестирование в Т. Если каждый инвестор приобретает Т и при этом Т не включает в себя инвестиций в каждый вид бумаг, то получается, что никто не инвестировал в те бумаги, которые имели нулевую долю в Т. Это должно привести к тому, что курсы ценных бумаг с нулевой долей в Т упадут, вызвав рост их ожидаемой доходности до тех пор, пока в «касательном» портфеле их доля станет отличной от нуля.

В результате соотношение долей каждой бумаги в «касательном» портфеле в состоянии равновесия будет соответствовать соотношению долей бумаг в так называемом рыночном портфеле. Рыночный портфель – это портфель, состоящий из всех ценных бумаг, в котором доля каждой соответствует ее относительной рыночной стоимости. Относительная рыночная стоимость ценной бумаги равна ее совокупной рыночной стоимости, деленной на сумму совокупных рыночных стоимостей всех ценных бумаг.

Причина, по которой рыночный портфель занимает центральное место с модели оценки финансовых активов, заключается в том, что эффективное множество состоит из инвестиций в рыночный портфель в совокупности с желаемым количеством безрискового заимствования или кредитования. Таким образом, вполне правомерно можно определить «касательный» портфель как рыночный и обозначить его через М вместо Т. Теоретически, М состоит не только из обыкновенных акций, но и других видов инвестиций, таких, как облигации, привилегированные акции и недвижимость. Однако на практике под М понимают портфель, содержащий только обыкновенные акции.

В модели оценки финансовых активов простым образом определяется связь между риском и доходностью эффективных портфелей. Это наглядно представлено на рисунке 2.7. Точка М обозначает рыночный портфель, а r_>f> представляет собой безрисковую ставку доходности. Эффективные портфели находятся вдоль прямой, пересекающей ось ординат в точке с координатами (0, r_>f>) и проходящей через М, и образуются альтернативными комбинациями риска и доходности, получаемыми в результате сочетания рыночного портфеля с безрисковым заимствованием или кредитованием. Это линейное эффективное множество в данной модели известно под названием рыночная линия (Capital Market Line, CML). Все остальные портфели, не использующие рыночный портфель в комбинации с безрисковым заимствованием или кредитованием, будут лежать ниже рыночной прямой, хотя некоторые могут располагаться в н
епосредственной близости от нее.

Рисунок 2.7 – Рыночная линия

Наклон CML равен разнице между ожидаемой доходностью рыночного портфеля и безрисковой бумаги (r_>M> – r_>f>), деленной на разницу их рисков (_>M> – 0), или (r_>M> – r_>f>)/_>M> . Так как CML пересекает вертикальную ось в точке с координатами (0, r_>f>), то уравнение CML имеет вид:

, (31)

где r_>p> – ожидаемая доходность эффективного портфеля;

_>p> – среднеквадратичное отклонение эффективного портфеля.

Рыночная линия представляет собой равновесное соотношение ожидаемой доходности и среднеквадратичного отклонения для эффективных портфелей. Отдельные рискованные бумаги всегда будут находиться ниже этой прямой, так как единичная рискованная бумага сама по себе является неэффективным портфелем. В модели формирования курсов на фондовом рынке не подразумевается определенной связи между ожидаемой доходностью и среднеквадратичным отклонением (т.е. общим риском) для каждой отдельной ценной бумаги. Для того чтобы сказать больше об ожидаемой доходности, необходим более глубокий анализ.

В модели оценки финансовых активов каждый инвестор обладает рыночным портфелем и его интересует среднеквадратичное отклонение своего портфеля, так как от него будет зависеть наклон CML, а следовательно, и размер инвестиций инвестора в рыночный портфель. Вклад каждой бумаги в среднеквадратичное отклонение рыночного портфеля зависит от величины ковариаций бумаги с рыночным портфелем. В соответствии с этим для каждого инвестора становится понятным, что величина допустимого риска каждой бумаги определяется ковариацией этой бумаги с рыночным портфелем, _>iM>. Это означает, что инвесторы будут рассматривать бумаги с большим значением _>iM> как вносящие большой риск в рыночный портфель. Кроме того, отсюда также следует, что бумаги, среднеквадратичное отклонение которых велико, не обязательно вносят больше риска в рыночный портфель, чем бумаги с меньшей величиной среднеквадратичного отклонения.

Из этого следует, что ценные бумаги с большими значениями _>iM> должны обеспечивать пропорционально большую ожидаемую доходность, что должно заинтересовать инвестора в их приобретении.

Точная форма равновесной взаимосвязи между риском и доходом может быть записана в следующем виде:

, (32)

где r_>i> – ожидаемая доходность i-й ценной бумаги;

_>iM> – ковариация i-й ценной бумаги с рыночным портфелем.

На рисунке 2.8 (а) уравнение (32) описывает прямую, пересекающую вертикальную ось в точке с ординатой r_>f> и имеющую наклон (r_>M> – r_>f>)/²_>M>. Так как величина наклона положительна, то уравнение указывает на то, что курсы ценных бумаг с большим значением ковариаций с рыночным портфелем _>iM> будут обеспечивать большую ожидаемую доходность (r_>i>). Эта зависимость ковариации и ожидаемой доходности известна под названием рыночная линия ценной бумаги (Security Market Line, SML).

Р
исунок 2.8 – Рыночная линия ценной бумаги

Уравнение SML может быть записано также и в следующей форме:

, (33)

где _>iM> – бета-фактор из индексной модели Шарпа.

Уравнение (33) представляет собой иную форму записи уравнения SML, что видно из рисунка 2.8 (б). Хотя обе прямые пересекают ось ординат в одной и той же точке, они имеют различный наклон. Наклон прямой, описанной уравнением (33), равен (r_>M> – r_>f>), а описанной уравнением (32) – (r_>M> – r_>f>)/²_>M>

Одно из свойств коэффициента «бета» портфеля заключается в том, что он представляет собой взвешенное среднее коэффициентов «бета» входящих в него ценных бумаг, где в качестве весов выступают доли инвестиции в эти бумаги. Выражение для вычисления коэффициента «бета» портфеля выглядит следующим образом:

. (34)

Ожидаемая доходность портфеля представляет собой взвешенную среднюю ожидаемых доходностей входящих в его состав ценных бумаг, где в качестве весов представлены доли инвестирования в эти бумаги. Это означает, что так как каждая бумага лежит на SML, то на этой же прямой будет лежать и каждый портфель. Не только каждая бумага, но и каждый портфель должны находиться на прямой, имеющей положительный наклон, где в качестве оси ординат выбрана ожидаемая доходность, а в качестве оси абсцисс – коэффициент «бета». Следовательно, получается, что эффективные портфели лежат как на CML, так и на SML, а неэффективные лежат на SML, но ниже CML.

Индексная модель Шарпа была описана в разделе 2.3. В ней предполагалось, что доход по обыкновенной акции связан с доходом по рыночному индексу.

Естественно задаться вопросом о взаимосвязи индексной модели рынка и модели оценки финансовых активов. Прежде всего следует заметить, что в обеих моделях величина наклона именуется как «бета» и обе каким-то образом связаны с рынком. Однако между ними существует два значительных различия.

Первое заключается в том, что индексная модель рынка является факторной моделью. И в отличие от модели оценки финансовых активов она не является равновесной моделью, описывающей процесс формирования курсов ценных бумаг.

Второе состоит в том, что рыночная модель использует рыночный индекс, в то время как САРМ-модели – рыночный портфель. Рыночный портфель сочетает в себе все обращающиеся на рынке бумаги, а рыночный индекс – только ограниченное их число. Поэтому концептуально коэффициент _>iI> из рыночной модели отличается от коэффициента _>iM> из модели оценки финансовых активов. Это связано с тем, что «бета» в рыночной модели измеряется относительно рыночного индекса, а «бета» в САРМ-модели – относительно рыночного портфеля. На практике, однако, в связи с тем, что точно определить структуру рыночного портфеля не удается, используют рыночный индекс. Поэтому «бету», определенную с помощью рыночного индекса, несмотря на концептуальное различие, принимают в качестве оценки «беты» в модели оценки финансовых активов.

2.6Теория арбитражного ценообразования

Целью арбитражных стратегий является использование различий в цене на ценные бумаги одного или родственного типа на различных рынках или сегментов рынков с целью получения прибыли. Арбитраж обычно состоит из продажи ценной бумаги по относительно высокой цене и одновременной покупки такой же ценной бумаги (или ее функционального эквивалента) по относительно низкой цене.

Арбитражная деятельность является важной составляющей современных эффективных рынков ценных бумаг. Поскольку арбитражные доходы являются безрисковыми по определению, то все инвесторы стремятся получать такие доходы при каждой возможности. Правда, некоторые инвесторы имеют большие ресурсы и наклонности для участия в арбитраже, чем другие. Однако для реализации и исчерпания арбитражных возможностей (вследствие покупок и продаж акций) достаточно меньшего числа инвесторов, чем имеется желающих принять участие в этих операциях.

Сущность арбитража проявляется при рассмотрении различных цен на определенную ценную бумагу. Однако «почти арбитражные» возможности могут существовать и у похожих ценных бумаг или портфелей. Определить, подходит ли ценная бумага или портфель для арбитражных операций, можно различными способами. Одним из них является анализ общих факторов, которые влияют на курс ценных бумаг.

Факторная модель подразумевает, что ценные бумаги или портфели с одинаковыми чувствительностями к факторам ведут себя одинаково, за исключением внефакторного риска. Поэтому ценные бумаги или портфели с одинаковыми чувствительностями к факторам должны иметь одинаковые ожидаемые доходности, в противном случае имелись бы «почти арбитражные» возможности. Но как только такие возможности появляются, деятельность инвесторов приводит к их исчезновению.

В качестве основных данных в модели используются общие факторы риска, например показатели: развития экономики, инфляции и т.д. Проводятся специальные исследования: как курс определенной акции в прошлом реагировал на изменение подобных факторов риска. При помощи полученных соотношений предполагается, что можно рассчитать поведение акций в будущем. Естественно, для этого используют прогнозы факторов риска.

В данной модели ожидаемый доход акции зависит не только от одного фактора (-фактора), а определяется множеством факторов. Вместо дохода по всему рынку рассчитывается доля по каждому фактору в отдельности. Исходным моментом является то, что средняя чувствительность фактора равна 1,0. В зависимости от восприимчивости каждой акции к различным факторам изменяются соответствующие доли дохода. В совокупности они определяют общий доход акции.

Согласно модели в условиях равновесия, обеспечиваемых при помощи арбитражных стратегий, ожидаемый доход r_>i>, складывается из процентов по вкладу без риска _>0> и определенного количества воздействующих факторов, проявляющихся на всем рынке в целом с соответствующими премиями за риск, которые имеют чувствительность относительно различных ценных бумаг:

(35)

где _>1>…_>n> – премии за риск вложения в i-ю ценную бумагу;

b_>i>_>1>… b_>in> – чувствительности i-й ценной бумаги к факторам;

n – количество факторов.

Чем сильнее реагирует акция на изменение конкретного фактора, тем больше может быть в положительном случае прибыль. Доход портфеля имеет следующий вид:

, (36)

где _>1>…_>n> – премии за риск вложения в данный портфель;

b_>p>_>1>… b_>pn> – чувствительности портфеля к факторам;

n – количество факторов.

За счет того, что рыночный портфель и индекс в данной модели не рассматриваются, она проще, чем предыдущие модели. Недостатком данной модели является следующее: на практике трудно выяснить, какие конкретные факторы риска нужно включать в модель. В настоящее время в качестве таких факторов используют темпы прироста валового внутреннего продукта, уровни инфляции, процентных ставок и цен на нефть. Особую трудность также составляет прогнозирование значений этих факторов.

3Формирование и оптимизация портфеля ценных бумаг
(на примере АБ «Дорожник»)

В настоящее время акционерный банк «Дорожник» временно прекратил операции по купле-продаже ценных бумаг (акций и облигаций). Это связано с приходом нового акционера – Урало-Сибирского банка, который является одним из наиболее динамично развивающихся институтов и работает сегодня по международным стандартам. Для приведения к этим стандартам в банке «Дорожник» проводится реорганизация. Однако в дальнейшем планируется возобновить работу с ценными бумагами в полном объеме.

Перед нами была поставлена задача осуществить выбор и обоснование методики по формированию портфеля ценных бумаг и провести практические расчеты, связанные с его созданием на примере построения портфелей облигаций и акций. Исходя из этого поставленной задачи в данной части дипломного проекта будет предложен портфель ценных бумаг, принципиальное значение которого будет в обосновании применения математических методов к формированию портфеля ценных бумаг.

В настоящее время рынок рублевых долговых инструментов представлен следующими основными секторами: рынок государственных и муниципальных облигаций, вексельный рынок, рынок корпоративных облигаций. Хотя по оборотам ведущую позицию занимает вексельный рынок (векселя, выпущенные банками, не попадают на рынок и используются либо для проведения различных зачетных операций, либо выпущены «проблемными банками»), большую часть долгового рынка занимается рынок ГКО/ОФЗ (рисунок 3.1).

Рынок акций является наиболее трудно предсказуемым, так как колебания курсов на нем могут достичь большого размаха. Таким образом, работа с акциями может принести как значительные убытки, так и большую прибыль. Поэтому применение математических моделей к портфелю акций является наиболее интересным с точки зрения получения оптимального портфеля, приносящего доход.

Рисунок 3.1 – Структура долгового рынка

Наряду с доходностью и риском банк уделяет большое внимание ликвидности. Хотя доходность по ГКО/ОФЗ находится на относительно низком уровне, они являются высоколиквидными ценными бумагами. Ликвидность портфеля акций также достижима путем отбора соответствующих ценных бумаг. Исходя из вышеназванных причин, для включения в состав совокупного портфеля ценных бумаг были выбраны акции и государственные облигации.

Формирование совокупного портфеля ценных бумаг банка будем проводить в несколько этапов. Первые два этапа включают в себя определение структуры оптимальных портфелей государственных облигаций и корпоративных акций. Третий этап является синтезом двух предыдущих и представляет собой определение конечной структуры общего портфеля. В завершении будет оценена эффективность применения моделей к данным рынкам путем определения полученного результата за период инвестирования.

3.1Формирование оптимальной структуры портфеля государственных облигаций

Для формирования оптимальной структуры портфеля государственных облигаций будем использовать параметрическую модель Марковица, описанную в параграфе 2.1. Эта методика оптимизирует структуру портфеля ценных бумаг на основе статистической информации.

В качестве периода накопления информации примем период с 1.10.2001г. по 29.03.2002г., который разобьем на 26 периодов длинной в одну неделю, т.е. значения показателей будем фиксировать каждую неделю периода накопления информации. Оптимальная структура портфеля формируется на апрель 2002 г.

Торги по государственным ценным бумагам, как это было описано в пункте 1.3.1, происходят на ММВБ. Список торгуемых инструментов на государственном секторе ММВБ на 01.04.2002 приведен в таблице А.1 приложения А.

Для рассмотрения целесообразности включения в портфель были отобраны ОФЗ 26001, ОФЗ 27002-27014, ОФЗ 28001 (итого 15 наименований). Примем эти ценные бумаги в качестве исходных для формирования оптимальной структуры портфеля государственных ценных бумаг.

Другие государственные облигации были отклонены по следующим причинам:

1. дата размещения выпусков позже даты начала периода накопления информации;

2. отсутствие котировок в течение длительного периода в следствии отсутствия торгов из-за низкой ликвидности.

Для обеспечения диверсификации портфеля ценных бумаг, количество ценных бумаг в портфеле должно быть не менее восьми. Портфель облигаций должен быть диверсифицирован по сроку до погашения облигаций. При отборе облигаций данные условия были соблюдены.

Исходными данными для реализации методики являются:

1. курс облигаций за период накопления информации (K_>it>);

2. рассчитанная на основе курса и календаря купонных выплат годовая эффективная доходность к погашению облигаций (r_>it>).

Исходные данные взяты из фактических биржевых котировок на ММВБ за период с 1.10.2001г. по 29.03.2002г. и представлены в таблицах А.2 и А.3 приложения А.

Для решения задачи нахождения оптимальной структуры портфеля государственных облигаций по модели Марковица используются следующие шаги:

1. нахождение математического ожидания и дисперсии эффективной доходности каждой облигации;

2. нахождение ковариаций между эффективными доходностями каждой пары облигаций;

3. определении структуры и местоположения эффективного множества;

4. выбор приемлемого соотношения доходности и риска;

5. нахождение доли инвестиций d_>i> в каждую облигацию.

Решение задачи оптимизации структуры портфеля ценных бумаг рассмотрено в параграфе 2.1. Рассмотрим поочередно все шаги решения.

Параметрическая модель Марковица допускает эффективную статистическую оценку. Параметры этой модели можно оценить исходя из имеющихся статистических данных за прошлые периоды.

Математическое ожидание эффективной доходности каждой облигации (r_>i>) вычисляется следующим образом:

. (37)

где r_>it> – эффективная доходность i-й облигации в период времени t, %, i = 1,…, 15;

t – номер периода диапазона накопления информации, t = 1, …, 26 ;

T – длительность периода накопления информации.

Стандартное отклонение эффективной доходности i-ой облигации (_>i>) определяется по формуле:

. (38)

Результаты вычисления математического ожидания и стандартного отклонения эффективной доходности каждой ценной бумаги представлены в таблице 3.1.

Ковариация между эффективными доходностями i-й и j-й облигаций (_>ij>) определяется по формуле:

, (39)

где r_>it> и r_>jt> – эффективные доходности, соответственно, i-й и j-й облигации в период времени t, %;

r_>i> и r_>j> – соответственно, математические ожидания эффективных доходностей i-й и j-й облигации, %.

Таблица 3.1 – Математическое ожидание и стандартное отклонение эффективной доходности облигаций

Облигация	Показатель
Математическое ожидание, %	Стандартное отклонение
ОФЗ 26001	16,52	1,014
ОФЗ 27002	14,28	0,906
ОФЗ 27003	14,37	0,885
ОФЗ 27004	14,58	0,718
ОФЗ 27005	14,49	0,836
ОФЗ 27006	14,75	0,799
ОФЗ 27007	14,84	0,746
ОФЗ 27008	15,26	0,721
ОФЗ 27009	15,31	0,688
ОФЗ 27010	15,40	0,666
ОФЗ 27011	15,60	0,852
ОФЗ 27012	16,42	1,121
ОФЗ 27013	16,20	0,957
ОФЗ 27014	16,09	0,906
ОФЗ 28001	16,33	1,010

Совокупность ковариаций i-й и j-й облигаций дает ковариационную матрицу доходностей (таблица 3.2).

Следующий этап в определении оптимальной структуры портфеля – построение эффективного множества (рисунок 3.2). Это множество было построено при помощи метода линейного программирования, т.е. при заданном значении доходности портфеля, рассчитанной по формуле (14), минимизировалась величина риска, т.е. стандартного отклонения портфеля, полученного при помощи формулы (15).

Рисунок 3.2 – Эффективное множество портфелей ОФЗ

Для определения точки нахождения на эффективном множестве оптимального портфеля необходимо построить кривые безразличия. Так как это достаточно трудно осуществить на практике, ограничимся лишь простым выбором этой точки на графике, исходя из собственных предположений.

Так как банки являются достаточно консервативными организациями, не склонными к большому риску, то искомая точка должна находиться в левой части кривой – с меньшим риском. Начиная с некоторого момента, кривая приобретает все более пологий вид, что свидетельствует о том, что при

Таблица 3.3
Облигация	Доля
ОФЗ 26001	0,183
ОФЗ 27004	0,018
ОФЗ 27005	0,126
ОФЗ 27007	0,027
ОФЗ 27008	0,030
ОФЗ 27009	0,044
ОФЗ 27010	0,031
ОФЗ 27012	0,540

дальнейшем увеличении доходности риск увеличивается нарастающими

темпами. Поэтому, нами было принято решение считать целесообразным при формировании оптимального портфеля для данного инвестора портфель с доходностью 16% годовых.

Оптимальный портфель облигаций, таким образом, имеет структуру, представленную в таблице 3.3 и на рисунке 3.3.

Риск портфеля, представленного в таблице 3.3, согласно формуле (15) и рисунку 3.2 составит величину _>p> = 0,52.

Рисунок 3.3 – Структура оптимального портфеля ОФЗ

Количество видов облигаций в портфеле составляет восемь видов, что является достаточным для диверсификации портфеля. Найденная структура оптимального портфеля облигаций в дальнейшем будет использоваться при составлении общего портфеля ценных бумаг АБ «Дорожник».

3.2Формирование оптимальной структуры портфеля акций

Для формирования портфеля акций будем использовать синтез сразу нескольких моделей. За основу примем модель оценки финансовых активов, которая использует рыночный портфель, содержащий все обращающие на рынке ценные бумаги. На практике, однако, в связи с тем, что точно определить структуру рыночного портфеля не удается, используют рыночный индекс. Поэтому «бету», определенную с помощью рыночной модели Шарпа, несмотря на концептуальное различие, принимают в качестве оценки «беты» в модели оценки финансовых активов.

Рыночный портфель в модели оценки финансовых активов является тождественным «касательному» портфелю в модели Тобина с безрисковым активом. Поэтому «касательный» портфель будем рассчитывать при помощи алгоритма Элтона-Грубера-Падберга, который применим к модели Тобина и значительно упрощает вычисления. За безрисковую ставку примем доходность оптимального портфеля государственных облигаций, рассчитанную в предыдущем параграфе. Хотя государственные ценные бумаги не являются полностью безрисковым инструментом, с некоторыми ограничениями мы можем сделать такое предположение. Тем более, это допущение сделает оба портфеля более взаимосвязанными.

Для рассмотрения были отобраны наиболее ликвидные акции российского фондового рынка. Ликвидность была оценена по формуле расчета агрегированного показателя ликвидности (формула 2). Результаты сведены в таблицу (3.4). В этой таблице также приведены обозначения, принятые в РТС (тикеры), и которые будут применяться в дальнейшем для краткости.

Хотя для применения алгоритма Элтона-Грубера-Падберга необходимо лишь значении «беты», интерес представляет и другие параметры регрессионного анализа рынка акций. Регрессионный анализ представляет собой наиболее распространенную методику анализа рынка, основные положения которого подробно рассмотрены в пункте 2.3.

Таблица 3.4 – Список акций, выбранных для рассмотрения

Название эмитента	Тикеры (P – привилег.)	Агрегированный показатель ликвидности
"ЕЭС России" РАО	EESR, EESRP	227 605,01
"Сибнефть"	SIBN	203 570,47
"ЛУКОЙЛ "Нефтяная компания"	LKOH	196 121,68
"Сургутнефтегаз"	SNGS, SNGSP	96 896,89
"Ростелеком"	RTKM, RTKMP	73 545,84
"Газпром"	GSPBEX	63 956,49
"Мосэнерго"	MSNG	59 818,43
"Сбербанк России"	SBER	30 339,70
"Норильский никель" ГМК	GMKN	11 928,16
"ЮКОС" НК	YUKO	6 111,41
"Татнефть"	TATN	2 945,06

Напомним, что зависимость доходности ценной бумаги от доходности индекса описывается формулой (18).

, (18)

где r_>i> – доходность ценной бумаги i за данный период;

r_>I> – доходность на рыночный индекс I за этот же период;

_>iI> – коэффициент смещения;

_> >_>iI> – коэффициент наклона;

_> >_>iI> – случайная погрешность.

Значения регрессионных показателей  и  зависят от глубины расчета, т.е. от размера временного ряда значений доходностей рыночного индекса и рассматриваемой ценной бумаги. Была выбрана глубина расчета показателей равная 6 месяцам (с 1.10.2001г. по 29.03.2002г), при этом доходности рассчитывались исходя из средневзвешенных ежедневных цен. Если в течении дня сделок по конкретной бумаге заключено не было, то средневзвешенная цена рассчитывается по формуле:

, (40)

где best_bid и best_ask – функции лучших котировок на покупку и продажу соответственно.

В качестве исходных данных приняты котировки акций в РТС, в качестве рыночного индекса – индекс РТС (таблица Б.1 приложения Б). Индекс РТС является единственным официальным индикатором Российской Торговой Системы. Индекс рассчитывается один раз в 30 минут в течение всей торговой сессии, начиная с 12:00 и заканчивая в 18:00. Значение индекса на 12:00 является значением открытия, на 18:00 – значением закрытия. Для расчетов фиксировалась значение индекса на момент закрытия торгов.

Для более точного регрессионного анализа за шаг расчет был принят один рабочий день. Доходность акций рассчитывалась по формуле (5). Результаты вычислений доходности представлены в таблица Б.2 приложения Б.

Параметры регрессионной модели рассчитывались по формулам (19-24). Математическое ожидание рассчитывалось как арифметическое среднее на основе исторических данных. Результаты сведены в таблицу 3.5.

Для наглядности на основе данных таблицы 3.5 построены гистограммы (рисунки 3.4 – 3.7).

Коэффициент «бета» предоставляет информацию о том, как прибыль по акции изменяется в соответствии с динамикой рыночной прибыли. Положительное значение бета-коэффициента означает тенденцию акций повышаться в том же направлении, что и рынок; отрицательное значение «бета» указывает на тенденцию движения против рынка. Показатель «бета» больше единицы определяет акцию, которая проявляет тенденцию в пропорциональном отношении изменяться в большей степени, чем рынок. Доход по ней повышается еще больше в момент общего повышения доходности рынка и падает в большей степени в момент общего снижения дохода рынка. Бета-коэффициент меньше единицы характеризует акцию, доход по которой менее изменчив, чем рынок.

Таблица 3.5 – Таблица коэффициентов

	Бета	Альфа	R2	СКО ошибки	Ошибка беты	Ошибка альфы	Математическое ожидание доходности , % в месяц
EESR	0,496	0,0025	0,148	0,025	0,095	0,0023	11,6
GSPBEX	0,705	0,0001	0,022	0,024	0,095	0,0023	9,1
LKOH	0,481	0,0011	0,151	0,023	0,089	0,0021	8,5
SBER	0,840	0,0080	0,065	0,027	0,104	0,0025	28,1
TATN	0,581	0,0007	0,070	0,020	0,078	0,0019	8,8
MSNG	0,471	0,0000	0,079	0,023	0,088	0,0021	6,0
RTKM	0,714	0,0038	0,087	0,021	0,081	0,0019	17,2
GMKN	0,661	0,0008	0,060	0,025	0,097	0,0023	9,9
SIBN	0,698	0,0065	0,041	0,033	0,128	0,0031	23,0
SNGS	0,936	-0,0010	0,128	0,013	0,051	0,0012	9,4
YUKO	0,739	0,0039	0,147	0,015	0,056	0,0013	17,7
EESRP	0,310	0,0082	0,007	0,092	0,358	0,0086	21,9
SNGSP	0,555	0,0009	0,202	0,019	0,074	0,0018	8,9
RTKMP	0,508	0,0059	0,039	0,025	0,098	0,0023	19,4

Основываясь на рисунке 3.4, можно сделать вывод о том, что в среднем у выбранных акций степень риска относительно невысока. Это следует из того, что коэффициент «бета» находится в пределах от 0 до 1. Хотя можно отметить, что простые акции «Сургутнефтегаза» лидировали в данной совокупности, и бета-коэффициент был всего лишь немногим меньше 1. Наиболее осторожный рост наблюдался у привилегированных акций РАО «ЕЭС России».

Коэффициент «альфа» характеризует ожидаемый доход на акцию в момент достаточной стабильности цен на акции в целом, когда доход рынка равен нулю. Альфа-коэффициент акций на рисунке 3.5 свидетельствует о том, что практически все акции, отобранные для рассмотрения были переоценены. Считается, что переоцененные акции будут корректироваться рынком уменьшением рыночной цены. Хотя акции Сбербанка при подсчете альфа-коэффициента показали свою переоцененность, в дальнейшем за период составления портфеля их цена возрастет на 23,8%.

Рисунок 3.4 – Бета-коэффициент акций

Рисунок 3.5 – Альфа-коэффициент акций

Принятие решений на основе альфа-коэффициента применяется при оперативном управлении портфеля ценных бумаг. Задачей же дипломного проекта является формирование оптимального портфеля на основе соотношения риска и дохода, поэтому отбор акций на основе альфа-коэффициента в данном случае не применим.

Коэффициент R-squared является коэффициентом детерминации и поэтому изменяется в пределах от 0 до 1. Его вычисление показало, что данных акции слабо коррелируют с рынком. Практически полное отсутствие корреляции показали привилегированные акции РАО «ЕЭС России».

Рисунок 3.6 – Коэффициент R-squared акций

Как уже описывалось выше, для составления оптимального портфеля достаточно определения математического ожидания как арифметической средней прошлых доходностей (рисунок 3.7). Математическое ожидание не отражает действительный прогноз доходности акций, который проводится на основе всех воздействующих факторов, но оно достаточно для применения математических моделей построения оптимального портфеля ценных бумаг.

Рисунок 3.7 – Математическое ожидание доходности акций

К специфике российского рынка акций относят ограниченное количество ликвидных инструментов, и схожесть их динамики. Таким образом, построение хорошо диверсифицированного портфеля по акциям затруднено, риск останется очень высоким, а его доходность будет зависеть от индекса РТС. Кроме того, альфа, бета-коэффициенты очень волатильны и неустойчивы.

Найдем теперь структуру оптимального портфеля акций с помощью пятишагового алгоритма Элтона-Грубера-Падберга. Алгоритм подробно описан в параграфе 2.4.1. Для проведения расчетов необходимо задать безрисковую дох-ть. За безрисковую ставку примем ожидаемую доходность портфеля ОФЗ, рассчитанную в предыдущем разделе и равную 16% годовых. Хотя в рассчитанном портфеле государственных облигаций присутствует некоторая доля риска, с некоторыми допущениями доходность по нему можно принять в качестве безрисковой.

Рассмотрим по порядку этапы составления оптимального портфеля и результаты расчетов сведем в таблицу 3.6.

1. Упорядочим ценные бумаги в порядке убывания отношения доходности к систематическому риску – отношение Трейнора (RVOL_>i>). Под доходностью в данном случае понимается «вознаграждение» за приобретение данной ценной бумаги, превышающее безрисковую доходность. Систематический риск выражен бета-коэффициентом ценной бумаги. RVOL_>i> рассчитывается с помощью формулы (27).

2. Наибольшее значение Трейнора было получено привилегированной акции РАО «ЕЭС России». Начиная с этой акции, будем добавлять ценные бумаги одну за другой и вычислять величину _>i> по формуле (28).

3. Сравнивая величины _>i> с соответствующими RVOL_>i> до тех пор, пока _>i> меньше RVOL_>i>, получим что начиная с i = 11 это соотношение изменяется на противоположное. Ценные бумаги с 1 по 10 будут иметь ненулевые веса в портфеле, а остальные – нулевые. Таким образом, _>10> является «ставкой отсечения» для отношения Трейнора.

4. После того как определено какие акции будут включены в портфель, необходимо определить в каких долях они будут представлены в этом портфеле. Для этого воспользуемся формулой (29) и вычислим величины Z_>i>, чтобы определить, с какими весами будут входить в портфель первые 10 ценных бумаг: Значения Z_>i> для i = 11, ..., 14 полагаются равными нулю

5. Разделив каждую Z_>i> на сумму Z_>i >(формула 30), получим веса, с которыми акции будут входить в портфель. Это сделать необходимо, так как сумма Z_>i> обычно не равна единиц. В нашем случае сумма Z_>i> = 54,82. Полученные значения X_>i> и являются долями ценных бумаг в портфеле.

Таблица 3.6 – Результаты расчетов оптимального портфеля акций

	i	RVOLi	Ф>i>	Z>i>	X>i>
EESRP	1	0,0306	0,0002	0,907	0,016
RTKMP	2	0,0165	0,0026	8,591	0,155
SBER	3	0,0147	0,0056	10,393	0,188
SIBN	4	0,0143	0,0062	5,485	0,099
Продолжение таблицы 3.6
	i	RVOLi	Ф>i>	Z>i>	X>i>
RTKM	5	0,0103	0,0065	7,512	0,136
YUKO	6	0,0103	0,0069	15,951	0,288
EESR	7	0,0097	0,0068	3,264	0,059
LKOH	8	0,0071	0,0065	1,204	0,032
SNGSP	9	0,0065	0,0061	1,110	0,010
TATN	10	0,0061	0,0060	0,411	0,009
GMKN	11	0,0056	0,0058	0,000	0,000
GSPBEX	12	0,0052	0,0056	0,000	0,000
MSNG	13	0,0048	0,0054	0,000	0,000
SNGS	14	0,0041	0,0051	0,000	0,000

На рисунке 3.8 отражена структура рассчитанного портфеля акций. Портфель состоит из непропорциональных частей: половина акций занимают 86,6% портфеля, другая половина – всего лишь 13,4%. Наибольшая доля выделена простым акциям компании «ЮКОС» – 28,8%. Однако, если учесть, что компания «Ростелеком» представлена в портфеле двумя видами акций (простые – 13,6%, привилегированные – 15,5%), то наибольшая доля данного портфеля принадлежит акциям именно этой компании (29,1%).

Ожидаемая доходность портфеля рассчитывается как взвешенное среднее математических ожиданий доходности входящих в него ценных бумаг, где в качестве весов взяты доли инвестиций, приходящихся на эти бумаги (формула 14). Прогнозируемая доходность портфеля m_>p> составит 26,6% в месяц (горизонт прогнозирования).

Бета-коэффициент портфеля представляет собой взвешенное среднее коэффициентов «бета» входящих в него ценных бумаг, где в качестве весов выступают доли инвестиции в эти бумаги (формула 34). Таким образом, совокупный бета-коэффициент полученного портфеля _>pM> равен 0,676, что свидетельствует об относительно невысокой степени риска.

Рисунок 3.8 – Структура оптимального портфеля акций

3.3Формирование оптимальной структуры совокупного портфеля ценных бумаг

Определение оптимальных портфелей государственных облигаций и акций не достаточно для составления конечного портфеля ценных бумаг. Необходимо также решить в каких пропорциях будут инвестироваться средства в эти портфели.

Для определения этих пропорций воспользуемся моделью Марковица, примененной при нахождении оптимального портфеля облигаций.

Характерной особенностью в данном случае будет то, что в качестве рассматриваемых единиц будут выступать не отдельные ценные бумаги, а сами портфели ценных бумаг. Поэтому интерес будет представлять динамика доходности портфелей, а динамика доходности отдельных их составляющих в расчет браться не будет.

При составлении портфеля акций тот факт, что цены были номинированы в долларах США, не влиял на конечный результат в виде доли ценной бумаги в портфеле. В данном случае при определении ковариаций с портфелем облигаций, выраженном в рублях, могут возникнуть расхождения. Поэтому возникает необходимость пересчета доходности акций, исходя из котировок акций в рублях. Курс доллара США представлен в таблице В.2 приложения В.

Для решения задачи нахождения оптимальной структуры совокупного портфеля ценных бумаг по модели Марковица будем использовать те же шаги, которые делались при составлении портфеля облигаций в параграфе 3.1.

Для построения эффективного множества возможных портфелей необходимо вычислить математическое ожидание и ковариационную матрицу.

За шаг расчета была принята одна неделя, но оценивалось значение доходности за месяц. Это целесообразно, так как больший шаг расчета повысит трудоемкость без существенного увеличения точности, а меньший шаг расчета существенно снизит диапазон данных до 6 величин. Оценивалась же доходность портфелей в месяц по причине того, что календарный месяц был выбран за горизонт расчета.

Доходность портфеля облигаций за месяц была найдена простым делением годовой доходности на 12. Недельная доходность портфеля акций была приведена к месячной путем умножения на количество недель.

Математическое ожидание доходности портфеля в данном случае рассчитано не как арифметическое среднее, а за него принята ожидаемая доходность, полученная в предыдущем параграфе. Она является более точной величиной, так как при расчетах был использован шаг в один рабочий день. Ряд доходностей (таблица В.1 приложения В) дан для того, чтобы рассчитать матрицу ковариаций и, следовательно, определить риск портфеля.

Для составления ковариационной матрицы необходимо рассчитать среднеквадратическое отклонение доходности портфелей и коэффициент корреляции между ними (таблица 3.7).

Ковариации рассчитаны на основе формулы (16). Результаты сведены в таблице 3.8. Ковариации портфеля облигаций и портфеля акций равны среднеквадратическому отклонению, возведенному в квадрат, то есть дисперсии этих портфелей.

Таблица 3.7 – Исходные данные для оптимизации совокупного портфеля

Наименовании параметра	Портфель облигаций	Портфель акций
Математическое ожидание доходности, % в месяц	1,333	26,600
Среднеквадратическое отклонение	0,071	36,802
Коэффициент корреляции между портфелями	0,168

Таблица 3.8 – Ковариационная матрица

	Портфель облигаций	Портфель акций
Портфель облигаций	0,00497	0,43710
Портфель акций	0,43711	1354,38

На основе этих данных возможно построить эффективное множество портфелей. Математическое ожидание доходности портфеля определяется как средневзвешенное доходностей, где в качестве веса выступает доля инвестиций к отдельную ценную бумагу (формула 14). Риск каждого портфеля определен по формуле (15). Результаты расчетов приведены в таблице В.3 приложения В.

На основе данных таблицы В.3 приложения В возможно построить эффективное множество возможных совокупных портфелей ценных бумаг (рисунок 3.9).

Теперь необходимо определить местоположение оптимального портфеля, то есть выбрать приемлемое соотношение доходности и риска.

Так как банки являются организациями, не склонными к большому риску, то искомая точка должна находиться в левой части кривой – с меньшим риском. Начиная с некоторого момента, кривая приобретает все более пологий вид, что свидетельствует о том, что при дальнейшем увеличении доходности риск увеличивается нарастающими темпами. Поэтому, целесообразно за оптимальный портфель для данного инвестора принять портфель с доходностью 15,2%.

Таким образом, в данном портфеле облигации имеют 45%, а акции представлены 55%.

Рисунок 3.9 – Эффективное множество совокупных портфелей

До сих пор состав портфеля определялся в относительных величинах. Для последующей оценки результатов необходимы абсолютные значения. Поэтому необходимо определить количественный состав портфелей. Для этого необходимо выбрать сумму инвестируемых средств.

В период, когда банк «Дорожник» активно занимался операциями купли-продажи ценных бумаг, сумма инвестируемых средств доходила до 15% от валюты баланса. На начало 2002 года валюта баланса составляла около 340 млн. рублей. Считаю целесообразным взять за размер инвестирования сумму в 5 млн. рублей, что составляет приблизительно 1,5% валюты баланса и соизмеримо с величиной статей отчетности.

Таким образом, учитывая, что 45% средств инвестируется в ОФЗ, а 55% – в акции, получим, что 2250 тыс. руб. должно быть направлено на покупку ОФЗ, а оставшаяся часть (2750 тыс. руб.) – на покупку акций.

Количество облигаций для покупки рассчитывается по формуле:

, (41)

где K_>i> – количество ценных облигаций, шт.;

d_>i> – доля портфеля, занимаемая облигацией;

S – сумма средств, инвестируемая в портфель, руб.;

P_>%> – цена облигации, в % от номинала;

N – номинал облигации, руб.

Данные для расчета и результаты сведены в таблицу 3.9.

Таблица 3.9 – Расчет количества облигаций для покупки

Облигация	Доля инвестиций	Сумма инвестируемых средств, руб.	Номинал, руб.	Цена на 01.04.02, % от номинала	Количество, шт.
ОФЗ 26001	0,183	411750	1000	95,38	456
ОФЗ 27004	0,018	40500	10	100,23	4063
ОФЗ 27005	0,126	283500	10	98,95	28364
ОФЗ 27007	0,027	60750	10	97,79	6248
ОФЗ 27008	0,030	67500	10	96,57	7116
ОФЗ 27009	0,044	99000	10	96,66	10385
ОФЗ 27010	0,031	69750	10	95,36	7386
ОФЗ 27012	0,540	1217250	10	91,76	137922
Итого	1,000	2250076			201940

Так как количество облигаций округлялось до целого, сумма инвестируемых средств немного отличается от первоначальной. Таким образом стоимость портфеля облигаций на 01.04.2002 составляет 2250076,42 руб.

Для определения количества акций, включаемого в портфель, необходимо их цены перевести в рубли, так как котировки акций в РТС выражены в долларах США. Курс доллара США на 01.04.2002, установленный ЦБ РФ, составлял 31,1192 рубля. Количество акций в портфеле определяется аналогично облигациям, но в знаменателе берется рыночная цена в рублях без номинала. В таблице 3.10 отражены результаты расчетов.

Таблица 3.10 – Расчет количества акций для покупки в портфель

Акция	Доля инвестиций	Сумма инвестируемых средств, руб.	Цена на 01.04.2002	Количество, шт.
в долларах США	в рублях
EESRP	0,016	44000	0,12	3,83	11781
RTKMP	0,155	426250	0,71	21,93	19468
SBER	0,188	517000	138,05	4295,94	120
SIBN	0,099	272250	1,69	52,44	5200
RTKM	0,136	374000	1,26	39,26	9513
YUKO	0,288	792000	8,37	260,56	3043
EESR	0,059	162250	0,16	5,05	32130
LKOH	0,032	88000	14,58	453,77	193
SNGSP	0,010	27500	0,22	6,78	4066
TATN	0,009	24750	0,68	21,31	1135
Итого	1,000	2728379			86649

Аналогично облигациям, количество акций округлялось до целого. Таким образом стоимость портфеля акций на 01.04.2002 составляет 2728379,39 руб.

3.4Анализ результатов формирования портфеля ценных бумаг

Формирование портфелей ценных бумаг требует также оценки результатов. Оптимальная структура портфеля формировалась на апрель 2002 года. Оценим как изменилась стоимость портфеля государственных облигаций (таблица 3.11) и портфеля акций (таблица 3.12) за период расчета. Исходные данные для анализа изменений стоимости и доходности портфеля представлены в таблицах Г.1 и Г.2 приложения Г.

Рост стоимости портфеля государственных облигаций за апрель 2002г. составил 0,55%. Доходность к погашению облигаций на 01.04.2002 составила 15,78%, а на 30.04.2002 – 15,89%, что ниже ожидаемой доходности 16%. Наибольший вклад в рост стоимости портфеля внесла ОФЗ 27012, имеющая наибольшую долю в портфеле облигаций и показавшая наибольший рост среди остальных ОФЗ.

Таблица 3.11 – Расчет изменения стоимости портфеля ОФЗ

Облигация	Коли-чество, шт.	Цена, руб.	Стоимость, руб.	Изменение стоимости
01.04.02	30.05.02	01.04.02	30.05.02	в руб.	в %
ОФЗ 26001	456	953,80	955,00	434932	435480	547	0,13
ОФЗ 27004	4063	10,02	10,03	40723	40760	36	0,09
ОФЗ 27005	28364	9,90	9,92	280661	281342	680	0,24
ОФЗ 27007	6248	9,78	9,80	61099	61217	118	0,19
ОФЗ 27008	7116	9,66	9,70	68719	69039	320	0,47
ОФЗ 27009	10385	9,67	9,71	100381	100879	498	0,50
ОФЗ 27010	7386	9,54	9,57	70432	70654	221	0,31
ОФЗ 27012	137922	9,18	9,25	1265572	1275916	10344	0,82
Итого	201940			2322523	2335291	12768	0,55

Динамика доходности портфеля ОФЗ представлена на рисунке 3.10.

Рисунок 3.10 – Динамика доходности портфеля ОФЗ за апрель 2002 года

Облигации оцениваются не только по доходности к погашению, но как и другие ценные бумаги – по стоимости. Динамика стоимости портфеля облигаций представлена на рисунке 3.11, из которого видно, что в период составления портфеля наблюдалась тенденция роста рыночной цены облигаций.

Рисунок 3.11 – Динамика стоимости портфеля ОФЗ за апрель 2002 года

Для анализа результатов формирования портфеля акций цены были взяты в рублевом эквиваленте.

Рост стоимости портфеля акций за апрель 2002г. составил 14,7%. Ожидаемая доходность портфеля акций за месяц была 26,6%. Фактическая доходность портфеля меньше ожидаемой в 1,8 раза.

Динамика стоимости портфеля акций за апрель 2002г. представлена на рисунке 3.12. Хотя в середине периода наблюдался резкий рост цен, к концу периода имело место небольшое снижение стоимости портфеля акций. Это произошло в основном за счет акций YUKO, SIBN, RTKM и RTKMP. Исторический максимум стоимости портфеля акций наблюдался 24.04.2002 и на эту дату стоимость портфеля составила 3210,493 тыс.руб. Динамика цен закрытия акций представлена на рисунках Д.1–Д.13 приложения Д.

Таблица 3.12 – Расчет изменения стоимости портфеля акций

Акция	Коли-чество, шт.	Цена, руб.	Стоимость, руб.	Изменение стоимости
01.04.02	30.05.02	01.04.02	30.05.02	в руб.	в %
EESRP	11781	3,83	3,93	45121	46299	1178	2,6
RTKMP	19468	21,93	23,5	426933	457498	30564	7,2
SBER	120	4295,94	5329,73	515512	639567	124054	24,1
SIBN	5200	52,44	57,63	272688	299676	26988	9,9
RTKM	9513	39,26	46,22	373480	439690	66210	17,7
YUKO	3043	260,56	305,4	792884	929332	136448	17,2
EESR	32130	5,05	4,71	162256	151332	-10924	-6,7
LKOH	193	453,77	556,46	87577	107396	19819	22,6
SNGSP	4066	6,78	6,94	27567	28218	650	2,4
TATN	1135	21,31	25,46	24186	28897	4710	19,5
Итого	86649			2728208	3127908	399700	14,7

Рисунок 3.12 – Динамика стоимости портфеля акций за апрель 2002 года

Общая стоимость портфеля на 01.04.2002 составила 5050731 руб., на 30.04.2002 – 5463199 руб. Абсолютное значение прироста равно 412468 руб. Темп прироста стоимости портфеля составил 8,17%, что ниже ожидаемого значения (15,2%) в 1,86 раза.

Таблица 3.13 – Результаты составления портфеля

Финансовый актив	Стоимость, руб.	Прибыль за период
01.04.2002	30.04.2002	в руб.	%
Облигации	2322523	2335291	12768	0,55
Акции	2728208	3127908	399700	14,65
Портфель	5050731	5463199	412468	8,17

Динамика стоимости совокупного портфеля ценных бумаг за апрель 2002 представлена на рисунке 3.13. Она практически полностью идентична динамики стоимости портфеля акций. Это объясняется тем, что колебания цен акций намного превышали колебания цен облигаций. Это еще раз подтверждает, что государственные облигации менее рискованны и поэтому приносят низкий доход.

Рисунок 3.13 – Динамика стоимости совокупного портфеля за апрель 2002 года

Исторический максимум стоимости совокупного портфеля ценных бумага, как и портфеля акций, наблюдался 24.04.2002 и на эту дату стоимость портфеля составила 5541,506 тыс.руб.

Таким образом, можно сделать вывод, что применение математических моделей не означает гарантированных результатов. Однако, несмотря на неточность прогнозов, модели оптимизации структуры портфеля ценных бумаг, помогают достичь приемлемого уровня доходности и риска и сохранить средства, по крайней мере при растущем рынке. Анализ проводился в период роста рынка акций (а именно они влияли на стоимость общего портфеля), поэтому нельзя сделать вывод, защитит ли применение этих моделей от убытков или нет.

Более точного результата прогнозов можно достичь применяя более глубокий фундаментальный анализ, но он в свою очередь требует относительно высоких затрат и наличие большого опыта. Поэтому принимая решение о стиле, методе, модели инвестирования необходимо соотнести генерируемые затраты и приобретаемые выгоды.

4Безопасность жизнедеятельности

Важным моментом в комплексе мероприятий направленных на совершенствование условий труда являются мероприятия по охране труда. Для успешного воплощения в жизнь всех мероприятий по охране труда необходимы знания в области физиологии труда, которые позволяют правильно организовать процесс трудовой деятельности человека.

В данном разделе дипломного проекта освещаются основные вопросы техники безопасности и экологии труда. В качестве примера оптимального рабочего места пользователя ПЭВМ приводится анализ характеристик конкретного помещения.

Существуют потенциально опасные и вредные производственные факторы. Опасным называется производственный фактор, воздействие которого на работающего человека в определенных условиях приводит к травме или другому внезапному резкому ухудшению здоровья. Если же производственный фактор приводит к заболеванию или снижению трудоспособности, то его считают вредным. В зависимости от уровня и продолжительности воздействия вредный производственный фактор может стать опасным.

Основными факторами, определяющими условия труда операторов ПЭВМ, являются:

1. Видимое излучение, блики и мерцание экрана, которые способствуют возникновению близорукости и переутомлению глаз, мигрени и головной боли, повышают раздражительность, нервное напряжение и могут вызывать стрессы.

2. Низкочастотное поле, которое может являться причиной заболеваний кожи; может измениться биохимическая реакция в крови на клеточном уровне.

3. Электростатическое поле, способное изменять и прерывать клеточное развитие; может стать причиной злокачественных опухолей; отмечена повышенная частота заболевания глаукомой.

4. Нерациональная организация рабочего места, несоответствие клавиатуры требованиям эргономики, которые вызывают быстрое утомление, болезненность и одеревенелость мышц шеи или плечевого пояса, боль в спине, «дискомфорт» в мышцах рук и ног.

5. Положительно заряженными ионами кислород, приводящий к ухудшению здоровья, угнетению нервной системы, наступает гипоксия.

6. Наличие бактерий. грибков, плесени, иных микроорганизмов и спор в воздухе. Количество микроорганизмов в воздухе практически не нормируется, однако давно установлено, что их присутствие повышает вероятность заболеваний.

7. Высокая концентрация озона промышленного происхождения, которая может привести к заболеваемости бронхитом.

8. Наличие шума, вибрации на рабочем месте.

9. Психофизические факторы такие, как умственное перенапряжение, перенапряжение зрительных и слуховых анализаторов, монотонность труда, эмоциональные перегрузки.

Словом, взаимодействие с ПЭВМ следует отнести к работам с тяжёлыми и вредными условиями труда. Целесообразно рассматривать проблему повышения безопасности и надежности работы человека в системе "человек – ПЭВМ" в комплексе мер , направленных на одновременное улучшение качества воздушной среды, организации рабочего места, использования защитных средств на мониторы и органы зрения, повышения защитных сил организма на внешнее неблагоприятное воздействие.

К рабочим местам с ПЭВМ применимы санитарно-гигиенические требования. В качестве наглядного примера рассмотрим помещение, в котором происходила работа над дипломом. Рассматриваемый объект – отдельная комната в жилом помещении.

Размеры помещения составляют: длина 5,4 м, ширина 5 м, высота 3 м. Общая площадь равна 27 кв.м., а объем равен 81 куб.м, что соответствует санитарным нормам СН 245-71, которые устанавливают на одного работающего, объем производственного помещения не менее 20 куб.м. Помещение также соответствует размещаемому в нем комплекту технических средств.

В помещении в течение всего года поддерживаются нормальные значения температуры, влажности воздуха, и скорости движения воздуха, благодаря соответствующим мерам. Для повышения влажности в помещении на расстоянии 1,5 м от компьютера размещены цветы.

Снижение уровня шума, проникающего в помещение извне, достигнуто увеличением звукоизоляции ограждающих конструкций, уплотнением по периметру притворов окон, дверей.

Рациональное цветовое оформление помещения направленно на улучшение санитарно-гигиенических условий труда, повышение его производительности и безопасности. Окраска помещений влияет на нервную систему человека, его настроение и в конечном счете на производительность труда. Окраска стен светло-розовая, потолка – белая, пол – паркетный, светло-коричневый. Цветовое оформление выполнено с учетом рекомендаций СН-181-70: цвета стен, потолка, пола гармонируют между собой. С точки зрения цветотерапии, розовый и светло-коричневый цвета улучшают настроение, положительно влияют на нервную систему и внутренние органы. Освещение помещения и оборудования мягкое, без блеска.

Искусственное освещение в помещении эксплуатации ПЭВМ осуществляется системой общего равномерного освещения. Общее освещение выполнено в виде сплошных или прерывистых линий светильников, расположенных сбоку от рабочих мест, параллельно линии зрения пользователя. Источник света в помещении – 10 ламп накаливания мощностью 40 Вт, высота подвески светильников равна 3 м, а расстояние между светильниками – 1-1,5 м.

Применяется система комбинированного освещения (к общему освещению дополнительно устанавливаются светильники местного освещения, предназначенные для освещения зоны расположения документов) для удобства работы с документами, что разрешено санитарными нормами.

Установлен светильник местного освещения (люминесцентная лампа) для подсветки документов, но с таким условием, что он не создает бликов на поверхности экрана и не увеличивает освещенность экрана.

Для обеспечения нормируемых значений освещенности в помещении использования ПЭВМ проводится чистка стекол оконных рам и светильников не реже двух раз в год и проводится своевременная замена перегоревших ламп.

Конструкция дисплея обеспечивает возможность фронтального наблюдения экрана путем поворота корпуса в горизонтальной плоскости вокруг вертикальной оси в пределах 30 градусов и в вертикальной плоскости вокруг горизонтальной оси в пределах 30 градусов с фиксацией в заданном положении.

Корпус дисплея и ПЭВМ, клавиатура и другие блоки к устройства ПЭВМ имеют матовую поверхность одного цвета и не имеют блестящих деталей, способных создавать блики, что соответствует требованиям, содержащихся в СанПиН, к покрытиям и материалам, из которых изготавливаются корпуса ПК и дисплеев. Предусмотрена окраска корпуса в спокойные мягкие тона с диффузным рассеиванием света.

Визуальные эргономические параметры ПЭВМ были достигнуты путем приобретения высококачественного ПЭВМ и его длительным предварительным тестированием, с целью выявить возможные дефекты.

Плоскость экрана компьютера расположена под прямым углом по отношению к плоскости оконных проемов так, что естественный свет падает сбоку, преимущественно слева. На окнах имеются жалюзи, что позволяет избегать лишних бликов на экране.

Высота рабочей поверхности стола для пользователей должна регулироваться в пределах 680-800 мм; при отсутствии таковой возможности высота рабочей поверхности стола должна составлять 725 мм.

В помещении установлен стол с высотой рабочей поверхности 725 мм, а также рабочее кресло с подъемно-поворотным устройством. Конструкция кресла обеспечивает регулировку высоты опорной поверхности сиденья в пределах 400-500 мм угла наклона сиденья и спинки. Кресло оборудовано подлокотниками, что сводит к минимуму неблагоприятное воздействие на кистевые суставы рук.

Рабочий стол имеет пространство для ног высотой 700 мм, шириной – 520 мм, глубиной на уровне колен – 450 мм и на уровне вытянутых ног – 660 мм.

Конструкция рабочего стола обеспечивает оптимальное размещение на рабочей поверхности используемого оборудования с учетом его количества и конструктивных особенностей, характера выполняемой работы.

Клавиатуру располагается на поверхности стола на расстоянии 100 мм от края, обращенного к пользователю, или на специальной регулируемой по высоте рабочей поверхности, отделенной от основной столешницы.

Периферийные устройства расположены в зоне досягаемости работающего.

Организация и оборудование рабочего места соответствует требованиям, приведенным в ГОСТ 12.2.032  78.

Для обеспечения оптимальной работоспособности и сохранения здоровья пользователей на протяжении работы с ПЭВМ устанавливаться перерывы.

Во время перерывов с целью снижения нервно-эмоционального напряжения, утомления зрительного анализатора, устранения влияния гиподинамии и гипокинезии выполняются комплексы упражнений.

С целью уменьшения отрицательного влияния монотонии применяется чередование операций осмысленного текста и числовых данных (изменение содержания работ) и чередование редактирования текстов и ввода данных (изменение содержания работы).

В соответствии с принятыми нормами в исследуемом помещении обеспечивается необходимый микроклимат, минимальный уровень шума, создано удобное и правильное с точки зрения эргономики рабочее место, соблюдены требования технической эстетики и требования к ПЭВМ.

Для большей производительности труда и меньшей утомляемости рекомендовано установить пюпитр и проводить перерывы в работе. Положение тела должно соответствовать направлению взгляда. Нижний уровень экрана должен находиться на 20 см ниже уровни глаз. Оптимальное расстояние от глаз до экрана компьютера — 75 .... 120см.

В целом условия труда в помещении соответствуют общепринятым нормам, работающему обеспечены комфорт и благоприятные условия труда.

Заключение

В данном дипломном проекте произведено формирование портфеля ценных бумаг акционерного коммерческого банка «Дорожник». Процесс формирования и оптимизации включал в себя следующие этапы:

1. Исследован теоретический материал по инвестиционному процессу, ценным бумагам и портфелю ценных бумаг. Рассмотрены основные ценные бумаги (акции и облигации, особенно государственные), так как именно они в последствии были включены в портфель. Причиной этому послужили низкий риск и ликвидность государственных облигаций и возможность получения высокого дохода по акциям.

2. Проведено исследование роли коммерческих банков на рынке ценных бумаг. Рассмотрен порядок работы по покупке-продаже ценных бумаг с практической точки зрения, то есть конкретный механизм осуществления сделок.

3. Определен тип портфеля, которому соответствует политика банка. Так как банк – это инвестор, не склонный к риску, портфель ценных бумаг данного объекта относится к портфелю среднего роста, который представляет собой сочетание надежных ценных бумаг и рискованных фондовых инструментов, состав которых периодически обновляется.

4. Подробно рассмотрена структура инвестиционного процесса, с помощью которой в дальнейшем были проведены расчетов.

5. Исследованы и проанализированы методики формирования оптимальной структуры портфеля ценных бумаг. Основные выводы, к которым пришла сегодня классическая портфельная теория можно сформулировать следующим образом:

1. эффективное множество содержит те портфели, которые одновременно обеспечивают и максимальную ожидаемую доходность при фиксированном уровне риска, и минимальный риск при заданном уровне ожидаемой доходности;

2. предполагается, что инвестор выбирает оптимальный портфель из портфелей, составляющих эффективное множество;

3. оптимальный портфель инвестора идентифицируется с точкой касания кривых безразличия инвестора с эффективным множеством;

4. диверсификация обычно приводит к уменьшению риска, так как стандартное отклонение портфеля в общем случае будет меньше, чем средневзвешенные стандартные отклонения ценных бумаг, входящих в портфель;

5. соотношение доходности ценной бумаги и доходности на индекс рынка известно как рыночная модель;

6. доходность на индекс рынка не отражает доходности ценной бумаги полностью. Необъясненные элементы включаются в случайную погрешность рыночной модели;

7. в соответствии с рыночной моделью общий риск ценной бумаги состоит из рыночного риска и собственного риска;

8. диверсификация приводит к усреднению рыночного риска;

9. диверсификация может значительно снизить собственный риск.

6. На основе проведенного анализа методик сделаны следующие выводы:

1. модель Блека неприменима для банка «Дорожник» в следствие ограничения на использование коротких позиций в торговле ценными бумагами;

2. индексная модель Шарпа применима в случае прогнозирования цен акций и анализа рынка и неприемлема для оптимизации структуры портфеля, так как ценные бумаги рассматриваются отдельно;

3. модель оценки финансовых активов хотя и отличается по существу от моделей Тобина и Шарпа, ее рыночный портфель может быть рассчитан при помощи этих моделей;

4. несмотря на то, что рыночный портфель и индекс в теории арбитражного ценообразования не рассматриваются, на практике трудно выяснить, какие конкретные факторы риска нужно включать в модель, а также спрогнозировать значения этих факторов;

5. лучшей методикой для формирования оптимальной структуры портфеля государственных облигаций является параметрическая модель Марковица. Одной из причин этого является то, что другие описанные методики применимы в основном лишь к акциям;

6. для формирования портфеля акций было решено использовать синтез сразу нескольких моделей. За основу принята модель оценки финансовых активов, которая использует рыночный портфель, но на практике используют рыночный индекс, поэтому «бету» определяют с помощью рыночной модели Шарпа. Рыночный портфель является тождественным «касательному» портфелю в модели Тобина, поэтому «касательный» портфель было решено рассчитать при помощи алгоритма Элтона-Грубера-Падберга, который применим к модели Тобина.

7. Формирование портфеля ценных бумаг банка проводилось в три этапа: определение оптимальной структуры портфеля государственных ценных бумаг, акций и совокупного портфеля. Таким образом портфель имеет двухуровневую структуру.

8. На основе фактических биржевых котировок выпусков государственных ценных бумаг за период с октября 2001г. по март 2002г. (шаг расчета – одна неделя) найдена оптимальная структура портфеля государственных ценных бумаг на начало апреля 2002г. Для этого были сделаны следующие шаги:

1. нахождение математического ожидания и дисперсии эффективной доходности каждой облигации;

2. построение ковариационной матрицы доходностей;

3. определении структуры и местоположения эффективного множества;

4. выбор приемлемого соотношения доходности и риска;

5. нахождение доли инвестиций в каждую облигацию.

9. Точка касания эффективного множества и кривой безразличия определялась экспертным методом. Таким образом, ожидаемая доходность к погашению портфеля облигаций составила 16% годовых, а риск составил величину 0,52. Наибольший удельный вес (54,1%) в структуре этого портфеля принадлежит ОФЗ 27012.

10. Для включение в рассмотрение третьего фактора – ликвидности, акции были отобраны по величине агрегированного показатели ликвидности. Проведен анализ акций с использованием индексной модели Шарпа, который показал следующее:

1. большинство акций в краткосрочном периоде показали более высокий риск, чем в долгосрочном. Это связано с тем, что последний квартал характеризовался бурным ростом рынка;

2. акции практически не коррелируют с рынком.

11. На основе выбранной модели и фактических биржевых котировок за период с октября 2001г. по март 2002г. (шаг расчета – один день) найдена оптимальная структура портфеля государственных ценных бумаг на начало апреля 2002г. Наибольшая доля в портфеле выделена простым акциям компании «ЮКОС» – 28,8%. Прогнозируемая доходность портфеля m_>p> составила 26,6% в месяц. Совокупный бета-коэффициент равен 0,676, что свидетельствует об относительно невысокой степени риска.

12. При формировании совокупного портфеля также была применена модель Марковица. Характерной особенностью в данном было то, что в качестве структурных единиц выступали не отдельные ценные бумаги, а сами портфели. Анализ показал, что 45% средств необходимо инвестировать в государственные облигации, а 55% – в акции.

13. Для определения количественного состава портфеля была выбрана сумму инвестируемых средств в 5 млн.руб., что составляет приблизительно 1,5% валюты баланса и соизмеримо с величиной статей отчетности. Таким образом, 2250 тыс. руб. должно быть направлено на покупку ОФЗ, а оставшаяся часть (2750 тыс. руб.) – на покупку акций.

14. Проведена оценка результатов составления оптимального портфеля ценных бумаг, которая показала следующее:

1. рост стоимости портфеля государственных облигаций за апрель 2002г. составил 0,55%. Доходность к погашению облигаций на 30.04.2002 составила 15,89%, что ниже ожидаемой доходности 16% и колебалась около 15,9-16% годовых. Наибольший вклад в рост стоимости портфеля внесла ОФЗ 27012, имеющая наибольшую долю в портфеле облигаций и показавшая наибольший рост среди остальных ОФЗ;

2. рост стоимости портфеля акций за апрель 2002г. составил 14,7%. Ожидаемая доходность портфеля акций за месяц была 26,6%;

3. прибыль, полученная от совокупного портфеля составила 412468 руб. Доходность портфеля за апрель составила 8,17%, наибольший вклад в рост стоимости внесли акции, но он ниже ожидаемого значения 15,2%. Динамика стоимости совокупного портфеля ценных бумаг практически полностью схожа с динамикой стоимости портфеля акций.

15. Таким образом, можно сделать вывод, что применение математических моделей не означает гарантированных результатов. Однако, несмотря на неточность прогнозов, модели оптимизации структуры портфеля ценных бумаг, помогают достичь приемлемого уровня доходности и риска и сохранить средства, по крайней мере при растущем рынке. Более точного результата прогнозов можно достичь применяя более глубокий фундаментальный анализ, но принимая решение о стиле, методе, модели инвестирования необходимо соотнести генерируемые затраты и приобретаемые выгоды.

Литература

1. Алехин Б. – Ликвидность и микроструктура рынка государственных ценных бумаг // Рынок ценных бумаг. – 2001. – №20. – С.20-30.

2. Банковское дело: Учебник. – 4-е изд., перераб. и доп. /под ред. В.И. Колесникова, Л.П. Кроливецкой. – М.: Финансы и статистика, 1999. – 464 с.

3. Буренин А.Н. Рынок ценных бумаг и производных финансовых инструментов: Учеб. пособие. – М.: Открытое общество, 1998. – 347 с.

4. Быльцов С.Ф. Настольная книга российского инвестора: Учеб. практ. пособие/ С.Ф. Быльцов. – СПб.: Бизнес-Пресса, 2000. – 506 с.

5. Ефимова М.Р., Петрова Е.В., Румянцева В.Н. Общая теория статистики: Учебник. – М.: ИНФРА-М, 1998. – 416 с.

6. Игнаточкин В. Нужно ли эффективное множество для оптимизации портфеля? // Рынок ценных бумаг. – 1998. – №8. – С. 62-65.

7. Касимов Ю.Ф. Основы теории оптимального портфеля ценных бумаг. – М.: Филинъ, 1998. – 144 с.

8. Миркин Я.М. Ценные бумаги и фондовый рынок. – М.: Перспектива, 1995. – 368 с.

9. Окулов В. Количественная оценка ликвидности акций компании на российском фондовом рынке // Рынок ценных бумаг. – 2000. – №23. – С. 43-49.

10. Петров В. Проблемы и перспективы внутреннего рынка государственных долговых обязательств // Рынок ценных бумаг – 2001. – №8. – С. 23-26.

11. Родионов Д. Стратегический обзор рынка // Рынок ценных бумаг. – 2001. – №17. – С. 31-36.

12. Рынок ценных бумаг: Учебник / Под ред. В.А. Галанова, А.И. Басова. – М.: Финансы и статистика, 1999. – 352 с.

13. Рэй К.И. Рынок облигаций: Торговля и управление рисками/ Пер. с англ. – М.: Дело, 1999. – 587 с.

14. Рязанов Б. Теории портфельного инвестирования и их применение в условиях российского рынка // Рынок ценных бумаг – 1998. – №2. – С. – 59-63.

15. Ряузов Н. Стратегия коммерческого банка на рынке ценных бумаг. Опыт Банка ЗЕНИТ // Рынок ценных бумаг – 2000. – №22. – С. 71-77.

16. Татьянников В. Как ведут себя измерители рисков на российском фондовом рынке // Рынок ценных бумаг. – 2001. – №21. – С. 57-61.

17. Третьяков А. Корреляционный анализ фондовых рынков // Рынок ценных бумаг. – 2001. – №15. – С.59-61.

18. Финансовый менеджмент: теория и практика: Учебник / Под ред. Е.С. Стояновой. – 5-е изд., перераб. и доп. – М.: Перспектива, 2000. – 656 с.

19. Ценные бумаги: Учебник / Под ред. В.И. Колесникова, В.С. Торкановского. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2001. – 448 с.

20. Ценные бумаги: Учеб. пособие / Н.И. Берзон, М.А. Кожевников, С.Е. Гуськов и др. – М.: ВШЭ, 1998. – 253 с.

21. Шарп У., Александер Г., Бэйли Дж. Инвестиции: Пер. с англ. – М.: ИНФРА-М, 2001. – 1028 с.

22. Aswath Damodaran. Estimating equity risk premiums. – Stern School of Business, 2001. – 24 p.

23. Aswath Damodaran. Estimating risk free rates. – Stern School of Business, 2001. – 11 p.

24. Bjarne Astrup Jensen. Mean variance efficient portfolios by linear programming: A review of some portfolio selection criteria of Elton, Gruber and Padberg. – Copenhagen Business School, 2001. – 29 p.

25. www.akm.ru – Информационное агентство AK&M.

26. www.cbr.ru – Банк России.

27. www.dor.ru – АБ «Дорожник»

28. www.micex.ru – Московская Межбанковская Валютная Биржа.

29. www.rts.ru – Фондовая биржа РТС.

30. www.web-invest.ru – Финансовая группа Web-invest.

Приложения

Таблица 3.2 – Ковариационная матрица доходностей ОФЗ

Код	26001	27002	27003	27004	27005	27006	27007	27008	27009	27010	27011	27012	27013	27014	28001
26001	1,029	0,073	0,203	0,211	0,014	0,271	0,199	0,328	0,275	0,257	0,495	0,810	0,779	0,794	0,670
27002	0,073	0,820	0,699	0,535	0,388	0,542	0,532	0,449	0,440	0,390	0,406	0,447	0,402	0,257	0,235
27003	0,203	0,699	0,784	0,614	0,502	0,627	0,594	0,522	0,505	0,485	0,532	0,566	0,501	0,370	0,406
27004	0,211	0,535	0,614	0,516	0,417	0,521	0,488	0,447	0,429	0,425	0,471	0,479	0,450	0,357	0,392
27005	0,014	0,388	0,502	0,417	0,699	0,405	0,345	0,329	0,306	0,312	0,317	0,312	0,135	0,130	0,137
27006	0,271	0,542	0,627	0,521	0,405	0,639	0,571	0,530	0,518	0,478	0,574	0,594	0,540	0,461	0,540
27007	0,199	0,532	0,594	0,488	0,345	0,571	0,556	0,498	0,488	0,461	0,537	0,489	0,479	0,395	0,461
27008	0,328	0,449	0,522	0,447	0,329	0,530	0,498	0,520	0,481	0,444	0,556	0,556	0,526	0,478	0,512
27009	0,275	0,440	0,505	0,429	0,306	0,518	0,488	0,481	0,473	0,435	0,540	0,517	0,495	0,446	0,501
27010	0,257	0,390	0,485	0,425	0,312	0,478	0,461	0,444	0,435	0,443	0,534	0,494	0,462	0,416	0,476
27011	0,495	0,406	0,532	0,471	0,317	0,574	0,537	0,556	0,540	0,534	0,726	0,754	0,678	0,659	0,694
27012	0,810	0,447	0,566	0,479	0,312	0,594	0,489	0,556	0,517	0,494	0,754	1,257	0,902	0,850	0,858
27013	0,779	0,402	0,501	0,450	0,135	0,540	0,479	0,526	0,495	0,462	0,678	0,902	0,916	0,818	0,827
27014	0,794	0,257	0,370	0,357	0,130	0,461	0,395	0,478	0,446	0,416	0,659	0,850	0,818	0,820	0,778
28001	0,670	0,235	0,406	0,392	0,137	0,540	0,461	0,512	0,501	0,476	0,694	0,858	0,827	0,778	1,020

Таблица А.2 – Рыночные цены ОФЗ за ноябрь 2001 – март 2002г. В % к номиналу

Дата	Выпуск ОФЗ
26001	27002	27003	27004	27005	27006	27007	27008	27009	27010	27011	27012	27013	27014	28001
01.10.2001	90,42	100,81	100,47	100,46	99,95	97,83	97,70	96,15	96,09	95,05	92,98	88,02	92,82	91,25	91,00
08.10.2001	90,72	101,13	100,88	100,85	99,96	98,51	98,46	96,69	96,80	95,72	93,50	88,61	92,47	91,88	91,68
15.10.2001	90,75	100,68	100,64	100,55	99,87	98,34	98,34	96,81	96,93	95,68	94,15	88,72	93,52	92,12	91,67
22.10.2001	90,92	100,94	100,92	100,85	98,85	98,92	98,87	97,13	97,03	95,94	93,98	88,90	93,80	92,33	91,90
29.10.2001	90,97	100,76	100,80	100,80	99,96	98,92	98,85	97,13	97,33	96,21	94,48	89,17	94,06	92,50	92,20
05.11.2001	91,38	100,79	100,75	100,76	99,95	99,27	99,19	97,71	97,60	96,66	94,95	89,77	94,08	92,78	92,65
12.11.2001	91,75	100,45	100,45	100,77	99,92	98,62	98,87	97,41	97,40	96,50	94,61	89,82	93,93	93,00	92,34
19.11.2001	91,75	100,59	100,60	100,90	100,00	99,01	99,03	97,81	97,88	96,81	94,91	89,72	94,00	92,90	92,51
26.11.2001	91,75	100,33	100,33	100,50	99,61	98,34	98,38	97,39	97,31	96,63	95,58	89,80	94,26	93,50	93,06
03.12.2001	92,31	100,25	100,40	100,55	99,62	98,44	98,35	97,18	97,32	96,48	95,33	90,01	93,98	94,15	92,88
10.12.2001	92,45	100,06	100,09	100,23	99,49	98,11	98,21	97,53	97,24	96,11	95,16	90,37	94,36	94,35	93,07
17.12.2001	92,94	100,16	100,15	100,14	99,32	98,16	98,39	96,69	96,72	95,79	94,60	90,35	94,03	93,58	92,66
24.12.2001	92,98	100,13	100,02	99,98	99,16	98,01	97,88	96,59	96,50	95,62	94,53	90,00	93,97	93,05	92,45
08.01.2002	92,98	100,23	100,46	100,81	99,78	99,27	99,04	99,79	97,53	96,89	95,71	91,45	93,98	93,54	93,79
14.01.2002	93,04	100,81	100,90	101,23	100,41	99,47	99,40	98,32	98,23	97,34	96,36	91,98	96,33	95,20	94,45
21.01.2002	94,27	100,86	100,91	101,42	100,27	99,21	99,30	98,18	98,00	91,21	96,01	92,30	96,14	95,24	94,27
28.01.2002	94,37	100,66	100,67	100,93	99,99	99,10	99,05	98,00	98,15	97,04	95,94	92,45	96,23	95,67	94,44
04.02.2002	94,84	100,73	100,73	101,20	100,17	99,43	99,22	98,07	98,24	97,46	96,39	92,89	96,87	96,34	95,45
11.02.2002	95,10	100,68	100,66	101,18	100,22	99,59	99,45	98,65	98,77	98,07	97,12	93,68	97,19	96,56	95,49
18.02.2002	95,10	100,56	100,69	101,00	100,03	99,25	99,45	98,42	98,32	97,40	96,63	93,65	97,31	96,61	95,35
26.02.2002	95,10	100,45	100,36	100,78	99,55	99,12	99,17	97,90	98,03	97,18	96,11	93,78	97,44	96,99	95,48
04.03.2002	95,18	100,42	100,42	100,70	98,86	99,02	99,07	97,85	97,87	96,77	95,94	92,59	97,42	96,07	95,21
11.03.2002	95,38	100,20	100,28	100,59	99,58	98,91	98,49	97,66	97,44	96,70	95,21	93,30	97,87	96,52	94,72
18.03.2002	95,38	99,97	99,98	99,97	99,11	98,14	97,83	97,07	96,80	95,25	94,10	91,53	94,94	94,96	92,92
25.03.2002	95,38	99,98	99,93	100,04	98,78	97,15	97,27	96,07	95,90	95,12	93,57	91,36	94,50	93,93	90,92
01.04.2002	95,38	100,07	100,15	100,23	98,95	98,00	97,79	96,57	96,66	95,36	94,38	91,76	94,35	93,92	92,76

Таблица А.3 – Доходность к погашению ОФЗ за ноябрь 2001 – март 2002г. В % годовых

Дата	Выпуск ОФЗ
26001	26002	26003	27002	27003	27004	27005	27006	27007	27008	27009	27010	27011	27012	27013	27014	28001
01.10.2001	17,89	18,19	19,70	14,21	14,77	15,09	14,54	15,79	15,94	16,43	16,42	16,47	17,23	17,64	17,61	17,69	17,78
08.10.2001	17,72	18,25	19,68	13,55	14,16	14,56	14,49	15,20	15,20	15,98	15,86	15,98	16,86	17,30	17,30	17,36	17,53
15.10.2001	17,79	18,32	19,23	14,32	14,53	14,90	14,56	15,36	15,21	15,86	15,80	15,99	16,39	17,36	17,17	17,27	17,38
22.10.2001	17,74	18,38	19,29	13,99	14,39	14,73	14,53	14,75	14,85	15,58	15,70	15,85	16,49	17,20	16,91	17,15	17,23
29.10.2001	17,80	18,43	18,97	14,03	14,11	14,62	14,35	14,71	14,84	15,41	15,43	15,65	16,12	16,99	16,82	17,03	17,02
05.11.2001	17,51	17,69	18,43	14,07	14,11	14,63	14,31	14,31	14,48	15,14	15,19	15,31	15,77	16,85	16,87	16,90	16,71
12.11.2001	17,27	17,75	18,45	14,74	14,65	14,58	14,42	14,94	14,76	15,37	15,33	15,40	16,06	19,67	16,89	16,76	16,90
19.11.2001	17,37	17,77	18,49	14,36	14,48	14,35	14,27	14,49	14,56	15,01	15,00	15,16	15,83	16,94	16,82	16,76	16,78
26.11.2001	17,48	17,13	18,48	14,89	15,01	14,88	14,75	15,28	15,19	15,34	15,45	15,26	15,47	16,81	16,66	16,49	16,47
03.12.2001	17,04	17,19	18,00	15,01	15,10	15,14	15,14	15,35	15,29	15,51	15,44	15,43	15,48	16,84	16,80	16,15	16,57
10.12.2001	17,00	17,28	17,47	15,43	15,47	15,38	14,83	15,47	15,42	15,56	15,47	15,69	15,58	16,63	16,62	16,00	16,43
17.12.2001	16,62	17,17	17,75	15,10	15,26	15,49	15,04	15,39	15,19	15,89	15,90	15,91	15,98	16,67	16,82	16,56	16,69
24.12.2001	16,68	17,32	17,18	15,39	15,53	15,72	15,40	15,53	15,73	16,50	16,08	16,03	16,09	17,00	16,91	16,68	16,82
08.01.2002	16,93	17,42	17,32	14,26	14,25	14,31	13,99	14,04	14,40	14,83	15,13	15,02	15,11	16,07	16,27	15,72	15,90
14.01.2002	16,97	17,50	16,57	12,98	13,06	13,46	13,28	13,83	13,90	14,36	14,52	14,62	14,63	15,71	15,66	15,66	15,48
21.01.2002	15,76	17,57	16,59	12,61	12,86	13,58	13,41	14,09	14,04	14,45	14,72	14,80	14,84	15,73	15,65	15,59	17,98
28.01.2002	15,75	17,58	16,42	13,17	13,43	14,00	13,78	14,16	14,33	14,59	14,52	14,87	14,92	15,45	15,43	15,23	15,44
04.02.2002	15,34	17,45	16,30	14,98	13,05	13,56	13,39	13,70	14,08	14,58	14,60	14,49	14,50	14,95	15,18	15,07	14,72
11.02.2002	15,16	17,16	16,02	12,98	13,10	13,36	13,38	13,43	13,74	13,98	14,10	13,98	13,98	14,63	14,98	14,98	14,66
18.02.2002	15,26	16,59	16,11	13,21	13,16	13,61	13,59	13,84	13,67	14,17	14,37	14,48	14,32	14,76	14,65	14,91	14,73
26.02.2002	15,38	16,67	16,50	13,68	14,04	14,04	14,32	13,94	14,12	14,68	14,53	14,66	14,65	14,69	14,43	14,54	15,01
04.03.2002	15,39	16,84	16,69	13,38	13,88	14,27	16,92	14,10	14,02	14,65	14,62	14,99	14,80	15,66	14,43	14,71	14,83
11.03.2002	15,26	16,92	16,68	14,31	14,33	14,43	14,41	14,20	14,99	14,98	15,11	15,60	15,37	15,20	14,74	14,99	15,15
18.03.2002	15,36	16,99	17,53	15,54	15,71	15,79	15,29	15,57	15,73	15,29	15,74	16,29	16,28	16,61	16,51	15,94	16,45
25.03.2002	15,45	16,99	17,55	16,03	15,88	15,60	16,02	16,66	16,50	16,58	16,89	16,39	16,82	16,94	16,27	16,34	16,91
01.04.2002	15,54	17,05	18,01	15,03	15,21	15,06	14,23	15,32	15,70	15,98	16,01	16,14	16,13	16,54	16,75	15,84	16,91

Приложение Б

Исходные данные для формирования портфеля акций

Таблица Б.1 – Котировки акций на фондовой бирже РТС и значение индекса РТС В долларах США

Дата	РТС	EESR	GSPBEX	LKOH	SBER	TATN	MSNG	RTKM	GMKN	SIBN	SNGS	YUKO	EESRP	SNGSP	RTKMP
01.10.2001	180	0,0888	0,4580	9,454	30,833	0,4346	0,0315	0,5039	13,190	0,5065	0,2257	3,2080	0,0588	0,1370	0,2501
02.10.2001	176	0,0866	0,4346	9,342	30,400	0,4191	0,0312	0,4867	11,912	0,5065	0,2212	3,2093	0,0569	0,1319	0,2260
03.10.2001	175	0,0845	0,4526	9,187	30,183	0,4102	0,0299	0,4594	10,801	0,5027	0,2157	3,2662	0,0578	0,1298	0,2155
04.10.2001	175	0,0864	0,4571	9,184	30,150	0,4149	0,0305	0,4645	10,471	0,5103	0,2176	3,2768	0,0588	0,1283	0,2200
05.10.2001	175	0,0864	0,4723	9,263	30,225	0,4129	0,0306	0,4893	9,983	0,5315	0,2207	3,3314	0,0570	0,1287	0,2331
08.10.2001	176	0,0850	0,4408	9,165	30,350	0,4046	0,0304	0,4895	9,945	0,5322	0,2179	3,3156	0,0558	0,1260	0,2375
09.10.2001	180	0,0870	0,4378	9,361	30,500	0,4148	0,0309	0,5021	10,366	0,5383	0,2195	3,3611	0,0555	0,1295	0,2371
10.10.2001	187	0,0892	0,4093	9,645	31,292	0,4248	0,0312	0,5230	10,970	0,5614	0,2295	3,4105	0,0576	0,1339	0,2495
11.10.2001	193	0,0938	0,4502	10,083	32,875	0,4432	0,0314	0,5502	11,057	0,5905	0,2436	3,5395	0,0599	0,1391	0,2536
12.10.2001	188	0,0938	0,4443	10,316	32,500	0,4449	0,0312	0,5538	11,253	0,5813	0,2492	3,5018	0,0599	0,1401	0,2667
15.10.2001	190	0,0915	0,4396	10,118	32,000	0,4393	0,0308	0,5410	11,373	0,5659	0,2439	3,4411	0,0603	0,1377	0,2600
16.10.2001	196	0,0933	0,4352	10,264	32,625	0,4411	0,0307	0,5553	11,492	0,5678	0,2480	3,4971	0,0597	0,1380	0,2695
17.10.2001	194	0,0971	0,4505	10,540	33,068	0,4655	0,0317	0,5863	12,259	0,6168	0,2574	3,5986	0,0626	0,1431	0,2716
18.10.2001	191	0,0932	0,4442	10,129	33,000	0,4522	0,0312	0,5712	11,960	0,6096	0,2496	3,5734	0,0598	0,1395	0,2640
19.10.2001	193	0,0925	0,4429	10,043	32,375	0,4455	0,0310	0,5873	11,514	0,6286	0,2454	3,4500	0,0591	0,1388	0,2716
22.10.2001	195	0,0953	0,4469	10,325	33,000	0,4650	0,0310	0,6165	11,636	0,6614	0,2525	3,6114	0,0618	0,1404	0,2743
23.10.2001	197	0,0982	0,4427	10,592	34,000	0,4808	0,0317	0,6082	11,675	0,5881	0,2560	3,6129	0,0619	0,1433	0,2725
24.10.2001	200	0,0989	0,4472	10,640	34,255	0,4920	0,0326	0,5973	12,443	0,6014	0,2578	3,6168	0,0639	0,1511	0,2700
25.10.2001	197	0,0970	0,4462	10,543	33,900	0,4836	0,0313	0,5921	12,116	0,6221	0,2508	3,6282	0,0640	0,1544	0,2718
26.10.2001	200	0,0965	0,4431	10,618	33,400	0,4841	0,0312	0,5901	12,085	0,6502	0,2509	3,6332	0,0630	0,1549	0,2718
29.10.2001	200	0,0963	0,4409	10,852	33,750	0,4918	0,0310	0,5904	12,175	0,6520	0,2551	3,6698	0,0638	0,1576	0,2728
30.10.2001	205	0,0968	0,4297	11,049	33,525	0,4984	0,0312	0,6004	12,559	0,6847	0,2557	3,7548	0,0641	0,1596	0,2730
31.10.2001	203	0,0982	0,4403	11,105	33,400	0,5011	0,0321	0,6061	12,592	0,6864	0,2569	3,7639	0,0635	0,1602	0,2725
01.11.2001	204	0,0996	0,4403	11,182	34,000	0,5023	0,0321	0,6282	12,566	0,6802	0,2562	3,7563	0,0640	0,1580	0,2785
02.11.2001	205	0,1025	0,4247	11,425	34,275	0,4992	0,0323	0,6368	12,361	0,6557	0,2533	3,8227	0,0675	0,1559	0,2800
05.11.2001	212	0,1064	0,4374	11,791	34,375	0,5036	0,0344	0,6537	12,139	0,6384	0,2551	3,9588	0,0680	0,1538	0,2982
06.11.2001	209	0,1086	0,4523	11,704	35,250	0,4950	0,0358	0,6579	12,131	0,6333	0,2539	4,0220	0,0692	0,1550	0,3150
08.11.2001	219	0,1169	0,4617	12,029	35,738	0,5014	0,0369	0,6825	12,201	0,6591	0,2607	4,1716	0,0749	0,1586	0,3356
09.11.2001	231	0,1238	0,4695	12,374	36,206	0,5149	0,0375	0,7247	13,199	0,6659	0,2671	4,3349	0,0794	0,1650	0,3601
12.11.2001	226	0,1351	0,4693	12,844	36,479	0,5133	0,0394	0,7726	13,287	0,6969	0,2785	4,3545	0,0845	0,1697	0,3793
Продолжение таблицы Б.1	В долларах США
Дата	РТС	EESR	GSPBEX	LKOH	SBER	TATN	MSNG	RTKM	GMKN	SIBN	SNGS	YUKO	EESRP	SNGSP	RTKMP
13.11.2001	243	0,1345	0,4670	12,934	37,177	0,5118	0,0383	0,7745	14,302	0,7126	0,2810	4,3827	0,0836	0,1772	0,3825
14.11.2001	219	0,1373	0,4913	12,943	38,042	0,5102	0,0391	0,7772	15,073	0,7185	0,2884	4,4152	0,0813	0,1720	0,3799
15.11.2001	212	0,1266	0,4756	11,563	35,750	0,5087	0,0358	0,7302	14,402	0,6558	0,2525	4,0220	0,0778	0,1632	0,3675
16.11.2001	213	0,1249	0,4673	10,962	35,750	0,5071	0,0354	0,7309	14,342	0,6531	0,2487	4,0293	0,0768	0,1565	0,3690
19.11.2001	218	0,1288	0,4706	11,038	36,050	0,5056	0,0362	0,7546	14,699	0,6507	0,2497	4,0779	0,0760	0,1602	0,3650
20.11.2001	221	0,1340	0,4654	11,397	36,225	0,5040	0,0365	0,7865	14,859	0,6511	0,2574	4,1235	0,0796	0,1619	0,3825
21.11.2001	219	0,1358	0,4681	11,227	36,750	0,5025	0,0362	0,7707	15,188	0,6431	0,2586	4,1221	0,0798	0,1688	0,3750
22.11.2001	231	0,1391	0,4655	11,614	39,627	0,5009	0,0362	0,7723	15,384	0,6407	0,2657	4,2194	0,0838	0,1726	0,3693
23.11.2001	225	0,1397	0,4697	11,633	40,885	0,4994	0,0365	0,7886	15,629	0,6436	0,2629	4,2456	0,0832	0,1706	0,3885
26.11.2001	227	0,1423	0,4707	11,382	40,464	0,5010	0,0366	0,8343	15,916	0,6605	0,2658	4,2377	0,0850	0,1748	0,3954
27.11.2001	226	0,1427	0,4761	11,276	41,583	0,5038	0,0367	0,8705	16,524	0,6576	0,2634	4,2443	0,0874	0,1718	0,4036
28.11.2001	222	0,1407	0,4804	11,060	42,433	0,4992	0,0362	0,8873	16,141	0,6468	0,2620	4,2574	0,0852	0,1693	0,4070
29.11.2001	227	0,1379	0,4957	10,766	44,250	0,4926	0,0356	0,8612	15,920	0,6451	0,2607	4,2420	0,0835	0,1697	0,4050
30.11.2001	227	0,1451	0,4970	11,173	46,550	0,4952	0,0358	0,9074	15,526	0,6473	0,2671	4,2778	0,0867	0,1720	0,4175
03.12.2001	231	0,1445	0,4972	11,166	46,445	0,4906	0,0356	0,9045	15,496	0,6473	0,2694	4,2566	0,0630	0,1708	0,4190
04.12.2001	235	0,1504	0,4687	11,543	49,961	0,4915	0,0367	0,9230	15,585	0,6540	0,2784	4,4167	0,0901	0,1758	0,4120
05.12.2001	238	0,1512	0,4927	11,709	51,125	0,4939	0,0380	0,9086	15,715	0,6555	0,2833	4,4560	0,0922	0,1750	0,4110
06.12.2001	237	0,1533	0,4913	11,913	56,029	0,5001	0,0388	0,9046	16,504	0,6564	0,2900	4,5212	0,0983	0,1789	0,4198
07.12.2001	240	0,1494	0,4903	11,694	59,974	0,4950	0,0384	0,8964	16,474	0,6568	0,2879	4,4777	0,0960	0,1790	0,4125
10.12.2001	241	0,1505	0,4939	11,857	67,692	0,4939	0,0383	0,8951	16,474	0,6654	0,2903	4,5309	0,1003	0,1793	0,4113
11.12.2001	238	0,1513	0,4598	11,801	64,500	0,4990	0,0394	0,8904	16,849	0,6637	0,2917	4,5976	0,1034	0,1795	0,4158
13.12.2001	230	0,1441	0,4644	11,399	62,544	0,4894	0,0377	0,8462	16,742	0,6390	0,2827	4,4994	0,1051	0,1760	0,4020
14.12.2001	231	0,1407	0,4646	10,966	59,636	0,4762	0,0369	0,8243	15,916	0,6367	0,2743	4,4584	0,1027	0,1739	0,4023
17.12.2001	236	0,1441	0,4810	11,242	64,017	0,4739	0,0372	0,8583	15,862	0,6364	0,2811	4,5079	0,1064	0,1760	0,4090
18.12.2001	238	0,1484	0,4944	11,286	66,000	0,4803	0,0387	0,8827	15,882	0,6367	0,2884	4,5721	0,1102	0,1778	0,4275
19.12.2001	243	0,1513	0,4987	11,370	70,967	0,4833	0,0389	0,8930	16,553	0,6433	0,2926	4,7734	0,1108	0,1797	0,4350
20.12.2001	243	0,1528	0,5002	11,620	71,566	0,4802	0,0391	0,9012	16,863	0,6487	0,2964	4,8825	0,1115	0,1850	0,4506
21.12.2001	250	0,1523	0,4999	11,570	69,850	0,4856	0,0391	0,9198	16,840	0,6575	0,2963	4,9283	0,1159	0,1838	0,4618
24.12.2001	251	0,1569	0,5066	11,899	71,500	0,4949	0,0409	0,9452	16,849	0,6706	0,3078	5,0080	0,1182	0,1925	0,4908
25.12.2001	250	0,1539	0,4972	11,791	73,893	0,4955	0,0410	0,9241	16,859	0,6946	0,3014	5,0309	0,1140	0,1903	0,4900
26.12.2001	252	0,1537	0,4976	11,756	73,500	0,4955	0,0408	0,9178	16,859	0,6946	0,3006	5,0811	0,1150	0,1900	0,4950
27.12.2001	256	0,1554	0,5082	11,847	74,875	0,4959	0,0414	0,9205	16,824	0,7199	0,3051	5,1236	0,1139	0,1948	0,4950
Продолжение таблицы Б.1	В долларах США
Дата	РТС	EESR	GSPBEX	LKOH	SBER	TATN	MSNG	RTKM	GMKN	SIBN	SNGS	YUKO	EESRP	SNGSP	RTKMP
28.12.2001	257	0,1566	0,5185	12,133	73,800	0,5055	0,0414	0,9220	16,874	0,7248	0,3095	5,1791	0,1153	0,1991	0,4830
29.12.2001	262	0,1573	0,5200	12,204	75,929	0,5079	0,0414	0,9228	16,944	0,7251	0,3119	5,1745	0,1170	0,2000	0,4826
03.01.2002	271	0,1633	0,5460	12,674	76,000	0,5255	0,0439	0,9457	17,412	0,7302	0,3205	5,2264	0,1186	0,2045	0,5035
04.01.2002	282	0,1735	0,5727	13,061	78,755	0,5680	0,0460	0,9838	18,161	0,7352	0,3341	5,3475	0,1243	0,2079	0,5050
08.01.2002	286	0,1796	0,5959	13,599	77,319	0,6094	0,0474	1,0514	19,252	0,8218	0,3492	5,5488	0,1279	0,2172	0,5307
09.01.2002	289	0,1785	0,5791	13,922	77,504	0,6079	0,0472	1,0564	18,810	0,8567	0,3515	5,6396	0,1320	0,2195	0,5298
10.01.2002	287	0,1743	0,5705	13,951	75,500	0,5810	0,0454	1,0155	18,232	0,8538	0,3481	5,6785	0,1308	0,2178	0,5266
11.01.2002	284	0,1742	0,5743	14,042	76,700	0,5774	0,0450	1,0186	18,232	0,8592	0,3483	5,9348	0,0855	0,2166	0,5313
14.01.2002	278	0,1682	0,5595	13,746	75,500	0,5527	0,0434	0,9883	17,404	0,8353	0,3387	5,8502	0,1300	0,2101	0,5250
15.01.2002	283	0,1659	0,5547	13,677	76,039	0,5500	0,0448	0,9848	16,873	0,8354	0,3297	5,7986	0,1273	0,2047	0,5022
16.01.2002	283	0,1684	0,5632	13,761	82,578	0,5563	0,0456	1,0006	16,978	0,8430	0,3300	5,9505	0,0933	0,2070	0,5061
17.01.2002	292	0,1702	0,5640	14,113	86,933	0,5552	0,0463	0,9995	16,928	0,8471	0,3340	5,9276	0,1319	0,2105	0,5100
18.01.2002	291	0,1699	0,5669	14,756	91,250	0,5596	0,0464	1,0211	16,718	0,8590	0,3354	5,9088	0,1304	0,2103	0,5173
21.01.2002	293	0,1691	0,5741	14,945	89,682	0,5708	0,0460	1,0170	16,477	0,8731	0,3350	5,9805	0,1315	0,2089	0,5168
22.01.2002	299	0,1727	0,5961	15,378	90,000	0,5846	0,0477	1,0638	16,481	0,8869	0,3479	6,1165	0,1325	0,2150	0,5350
23.01.2002	291	0,1724	0,6018	15,489	88,607	0,5798	0,0481	1,0875	16,468	0,8852	0,3414	6,0602	0,1335	0,2114	0,5522
24.01.2002	281	0,1667	0,5854	14,897	85,243	0,5346	0,0465	1,0706	15,465	0,8643	0,3217	5,8328	0,1285	0,2031	0,5517
25.01.2002	279	0,1607	0,5842	14,272	81,407	0,5042	0,0454	1,0547	15,073	0,8378	0,3197	5,8878	0,1222	0,1998	0,5425
28.01.2002	286	0,1592	0,5851	14,100	80,000	0,5032	0,0442	1,0525	15,180	0,8396	0,3228	5,9115	0,1226	0,2035	0,5296
29.01.2002	286	0,1636	0,6016	14,609	82,000	0,5130	0,0445	1,0730	15,879	0,8799	0,3316	6,2493	0,1289	0,2122	0,5434
30.01.2002	287	0,1597	0,5913	14,016	82,000	0,4977	0,0433	1,0432	15,595	0,8760	0,3222	6,1191	0,1281	0,2053	0,5263
31.01.2002	290	0,1627	0,5976	14,225	83,750	0,4989	0,0438	1,0480	15,820	0,8597	0,3275	6,2320	0,1294	0,2087	0,5500
01.02.2002	286	0,1587	0,5926	14,123	84,625	0,5090	0,0447	1,0797	16,527	0,8642	0,3276	6,3891	0,1293	0,2151	0,5511
04.02.2002	284	0,1522	0,5888	13,811	80,771	0,5002	0,0445	1,0809	16,451	0,8632	0,3261	6,5140	0,1300	0,2183	0,5505
05.02.2002	289	0,1499	0,5893	13,840	80,250	0,4972	0,0433	1,0691	16,234	0,8661	0,3231	6,4838	0,1293	0,2157	0,5430
06.02.2002	291	0,1538	0,5940	14,168	81,750	0,5034	0,0423	1,1219	16,274	0,8677	0,3291	6,6031	0,1291	0,2174	0,5694
07.02.2002	296	0,1538	0,6023	14,480	82,000	0,5061	0,0429	1,1452	16,993	0,8972	0,3291	6,6243	0,1261	0,2155	0,5730
08.02.2002	294	0,1540	0,6094	14,325	85,400	0,5082	0,0432	1,1501	17,775	0,9261	0,3262	6,6393	0,1220	0,2189	0,5830
11.02.2002	299	0,1533	0,6070	14,350	84,250	0,5076	0,0420	1,1700	17,584	0,9478	0,3268	6,6242	0,1196	0,2207	0,6029
12.02.2002	296	0,1534	0,6069	14,489	87,000	0,5218	0,0416	1,1818	17,604	1,0304	0,3359	6,6354	0,1175	0,2239	0,6100
13.02.2002	289	0,1513	0,6021	14,172	87,500	0,5202	0,0408	1,1456	17,633	0,9875	0,3327	6,6476	0,1175	0,2220	0,6000
14.02.2002	296	0,1506	0,5989	13,537	86,475	0,5253	0,0405	1,1334	17,514	1,0195	0,3310	6,5809	0,1180	0,2227	0,6137
Продолжение таблицы Б.1	В долларах США
Дата	РТС	EESR	GSPBEX	LKOH	SBER	TATN	MSNG	RTKM	GMKN	SIBN	SNGS	YUKO	EESRP	SNGSP	RTKMP
15.02.2002	297	0,1516	0,5979	13,413	88,225	0,5385	0,0397	1,1499	17,519	1,0432	0,3357	6,6110	0,1185	0,2233	0,6075
18.02.2002	290	0,1481	0,5936	12,883	86,198	0,5359	0,0395	1,1269	17,611	1,0482	0,3342	6,6236	0,1175	0,2208	0,6059
19.02.2002	285	0,1458	0,6014	12,714	86,750	0,5171	0,0392	1,1217	18,039	1,0500	0,3313	6,6092	0,1245	0,2215	0,6093
20.02.2002	287	0,1422	0,6015	12,243	86,525	0,5089	0,0374	1,0752	17,871	1,0361	0,3209	6,4793	0,1125	0,2157	0,5964
21.02.2002	289	0,1468	0,6071	12,473	85,750	0,5188	0,0379	1,0737	17,921	1,0552	0,3280	6,5499	0,1173	0,2143	0,5970
22.02.2002	297	0,1489	0,6140	12,836	90,000	0,5301	0,0391	1,1120	18,881	1,0772	0,3278	6,7335	0,1330	0,2135	0,6080
26.02.2002	294	0,1537	0,6430	12,905	91,156	0,5312	0,0401	1,1237	19,913	1,1646	0,3231	6,8707	0,1230	0,2206	0,6225
27.02.2002	292	0,1511	0,6544	12,454	90,375	0,5084	0,0402	1,1324	19,533	1,1637	0,3070	6,7634	0,1190	0,2049	0,6350
28.02.2002	295	0,1506	0,6656	12,217	89,300	0,5034	0,0389	1,1611	19,585	1,1612	0,3000	6,7867	0,1334	0,2025	0,6300
01.03.2002	321	0,1569	0,7105	12,527	92,537	0,5047	0,0409	1,1637	20,129	1,2451	0,3132	7,1645	0,1251	0,2139	0,6340
04.03.2002	318	0,1681	0,7706	12,953	97,036	0,5398	0,0428	1,2148	20,084	1,4718	0,3319	7,7477	0,1310	0,2201	0,6500
05.03.2002	317	0,1666	0,7669	12,978	95,435	0,5396	0,0425	1,2175	20,015	1,4300	0,3351	7,5737	0,1280	0,2201	0,6750
06.03.2002	321	0,1658	0,7676	13,039	93,250	0,5362	0,0422	1,2115	19,722	1,3318	0,3405	7,5811	0,1280	0,2224	0,6600
07.03.2002	331	0,1712	0,7789	13,332	96,000	0,5445	0,0436	1,2515	20,026	1,3890	0,3559	7,9806	0,1331	0,2276	0,6889
11.03.2002	319	0,1672	0,7539	13,146	98,106	0,5727	0,0419	1,2360	20,272	1,4396	0,3576	7,7081	0,1304	0,2298	0,7250
12.03.2002	323	0,1608	0,6669	12,896	97,000	0,5936	0,0410	1,1987	20,076	1,4342	0,3496	7,4789	0,1275	0,2230	0,7003
13.03.2002	323	0,1624	0,7162	13,144	96,250	0,6004	0,0406	1,1873	20,174	1,4390	0,3569	7,4994	0,1298	0,2214	0,7076
14.03.2002	337	0,1654	0,7466	13,071	98,363	0,6043	0,0406	1,1992	20,472	1,5576	0,3658	7,7619	0,1290	0,2281	0,7119
15.03.2002	344	0,1683	0,7637	13,424	103,190	0,6121	0,0415	1,2198	20,902	1,6906	0,3787	7,8987	0,1296	0,2325	0,7153
18.03.2002	347	0,1700	0,7645	13,907	109,459	0,6274	0,0424	1,2534	21,420	1,7547	0,3865	8,0878	0,1315	0,2384	0,7269
19.03.2002	347	0,1670	0,7340	13,703	107,159	0,6207	0,0440	1,2549	21,728	1,7569	0,3905	8,2461	0,1260	0,2330	0,7020
20.03.2002	339	0,1632	0,7223	13,431	106,708	0,5963	0,0440	1,2136	21,686	1,7502	0,3844	8,1836	0,1225	0,2284	0,6870
21.03.2002	345	0,1641	0,7167	13,549	110,188	0,5980	0,0435	1,2307	21,511	1,7325	0,3844	8,0206	0,1260	0,2296	0,7000
22.03.2002	348	0,1642	0,7165	13,880	120,752	0,6244	0,0436	1,2378	21,707	1,7325	0,3907	8,0250	0,1200	0,2312	0,7050
25.03.2002	334	0,1610	0,6981	13,723	121,104	0,6484	0,0420	1,2345	22,092	1,6963	0,3894	7,8183	0,1270	0,2272	0,6750
26.03.2002	338	0,1561	0,6929	13,238	122,057	0,6681	0,0406	1,2360	22,029	1,5723	0,3788	7,6424	0,1250	0,2258	0,6925
27.03.2002	343	0,1585	0,7035	13,901	128,284	0,6747	0,0414	1,2621	21,728	1,5682	0,3689	7,9356	0,1240	0,2232	0,7050
28.03.2002	351	0,1617	0,7101	14,409	138,050	0,6965	0,0423	1,2632	21,603	1,6436	0,3602	8,2411	0,1175	0,2200	0,7100
29.03.2002	350	0,1639	0,7295	14,637	136,375	0,6892	0,0426	1,2755	21,808	1,6980	0,3684	8,3909	0,1164	0,2198	0,7095
01.04.2002	349	0,1623	0,7234	14,582	138,048	0,6846	0,0424	1,2616	21,793	1,6850	0,3670	8,3730	0,1230	0,2180	0,7050

Таблица Б.2 – Изменение индекса РТС и цен акций В %

Дата	РТС	EESR	GSPBEX	LKOH	SBER	TATN	MSNG	RTKM	GMKN	SIBN	SNGS	YUKO	EESRP	SNGSP	RTKMP
02.10.2001	-2,22	-2,49	-5,11	-1,19	-1,41	-3,57	-1,11	-3,42	-9,69	0,00	-2,02	0,04	-3,08	-3,72	-9,62
03.10.2001	-0,57	-2,39	4,13	-1,66	-0,71	-2,14	-4,07	-5,60	-9,33	-0,75	-2,47	1,77	1,42	-1,63	-4,65
04.10.2001	0,00	2,25	1,00	-0,03	-0,11	1,16	1,97	1,11	-3,05	1,50	0,89	0,32	1,73	-1,14	2,09
05.10.2001	0,00	0,00	3,33	0,86	0,25	-0,47	0,39	5,35	-4,66	4,16	1,43	1,67	-2,98	0,31	5,97
08.10.2001	0,57	-1,68	-6,68	-1,05	0,41	-2,02	-0,62	0,03	-0,38	0,14	-1,27	-0,47	-2,19	-2,08	1,87
09.10.2001	2,27	2,41	-0,67	2,13	0,49	2,52	1,35	2,58	4,23	1,14	0,71	1,37	-0,45	2,78	-0,18
10.10.2001	3,89	2,49	-6,51	3,03	2,60	2,42	1,10	4,16	5,82	4,28	4,56	1,47	3,69	3,39	5,25
11.10.2001	3,21	5,18	9,98	4,54	5,06	4,33	0,71	5,20	0,80	5,18	6,15	3,78	4,03	3,89	1,62
12.10.2001	-2,59	-0,04	-1,30	2,32	-1,14	0,39	-0,80	0,66	1,76	-1,55	2,31	-1,07	0,10	0,70	5,17
15.10.2001	1,06	-2,45	-1,05	-1,93	-1,54	-1,26	-1,09	-2,31	1,07	-2,64	-2,16	-1,73	0,53	-1,70	-2,50
16.10.2001	3,16	2,04	-1,00	1,45	1,95	0,40	-0,42	2,63	1,04	0,33	1,71	1,63	-0,91	0,22	3,65
17.10.2001	-1,02	4,07	3,52	2,69	1,36	5,53	3,36	5,58	6,68	8,63	3,76	2,90	4,92	3,66	0,78
18.10.2001	-1,55	-4,05	-1,41	-3,90	-0,20	-2,85	-1,51	-2,58	-2,45	-1,17	-3,02	-0,70	-4,49	-2,48	-2,79
19.10.2001	1,05	-0,75	-0,29	-0,86	-1,89	-1,49	-0,70	2,82	-3,73	3,12	-1,67	-3,45	-1,17	-0,54	2,88
22.10.2001	1,04	3,05	0,89	2,81	1,93	4,38	-0,06	4,97	1,06	5,21	2,88	4,68	4,50	1,21	0,99
23.10.2001	1,03	2,96	-0,93	2,58	3,03	3,39	2,10	-1,34	0,33	-11,1	1,40	0,04	0,16	2,01	-0,65
24.10.2001	1,52	0,80	1,02	0,46	0,75	2,33	3,10	-1,79	6,59	2,27	0,71	0,11	3,30	5,49	-0,92
25.10.2001	-1,50	-1,95	-0,23	-0,92	-1,04	-1,72	-4,14	-0,88	-2,63	3,44	-2,71	0,31	0,03	2,15	0,65
26.10.2001	1,52	-0,56	-0,69	0,72	-1,47	0,11	-0,29	-0,33	-0,26	4,53	0,02	0,14	-1,49	0,36	0,00
29.10.2001	0,00	-0,19	-0,50	2,21	1,05	1,60	-0,48	0,04	0,75	0,26	1,67	1,01	1,19	1,72	0,37
30.10.2001	2,50	0,51	-2,54	1,81	-0,67	1,34	0,35	1,70	3,15	5,02	0,27	2,32	0,53	1,27	0,09
31.10.2001	-0,98	1,50	2,46	0,51	-0,37	0,55	3,02	0,95	0,27	0,26	0,45	0,24	-0,92	0,38	-0,18
01.11.2001	0,49	1,36	0,01	0,70	1,80	0,24	0,00	3,64	-0,21	-0,90	-0,26	-0,20	0,79	-1,35	2,20
02.11.2001	0,49	2,97	-3,55	2,17	0,81	-0,62	0,50	1,37	-1,63	-3,61	-1,16	1,77	5,47	-1,36	0,54
05.11.2001	3,41	3,74	3,00	3,20	0,29	0,87	6,60	2,65	-1,79	-2,63	0,71	3,56	0,67	-1,34	6,50
06.11.2001	-1,42	2,12	3,40	-0,74	2,55	-1,70	4,01	0,65	-0,07	-0,80	-0,45	1,60	1,78	0,78	5,64
08.11.2001	4,78	7,60	2,09	2,77	1,38	1,30	3,10	3,74	0,58	4,07	2,68	3,72	8,26	2,34	6,52
09.11.2001	5,48	5,95	1,70	2,87	1,31	2,68	1,57	6,18	8,18	1,03	2,45	3,91	6,05	4,01	7,32
12.11.2001	-2,16	9,09	-0,05	3,80	0,75	-0,30	5,29	6,61	0,67	4,66	4,26	0,45	6,41	2,87	5,33
13.11.2001	7,52	-0,45	-0,48	0,70	1,91	-0,30	-2,84	0,24	7,64	2,25	0,89	0,65	-1,03	4,42	0,84
14.11.2001	-9,88	2,11	5,19	0,06	2,33	-0,30	2,09	0,35	5,39	0,83	2,62	0,74	-2,80	-2,97	-0,67
Продолжении таблицы Б.2	В %
Дата	РТС	EESR	GSPBEX	LKOH	SBER	TATN	MSNG	RTKM	GMKN	SIBN	SNGS	YUKO	EESRP	SNGSP	RTKMP
15.11.2001	-3,20	-7,79	-3,19	-10,66	-6,02	-0,30	-8,39	-6,04	-4,45	-8,72	-12,44	-8,91	-4,34	-5,09	-3,27
16.11.2001	0,47	-1,32	-1,75	-5,20	0,00	-0,30	-1,28	0,09	-0,41	-0,42	-1,50	0,18	-1,29	-4,14	0,41
19.11.2001	2,35	3,09	0,71	0,69	0,84	-0,31	2,37	3,25	2,49	-0,37	0,40	1,21	-0,98	2,40	-1,08
20.11.2001	1,38	4,06	-1,12	3,26	0,49	-0,31	0,80	4,22	1,09	0,06	3,08	1,12	4,70	1,02	4,79
21.11.2001	-0,90	1,34	0,58	-1,49	1,45	-0,31	-0,85	-2,01	2,21	-1,22	0,46	-0,03	0,34	4,29	-1,96
22.11.2001	5,48	2,38	-0,56	3,45	7,83	-0,31	-0,03	0,21	1,29	-0,37	2,76	2,36	4,90	2,25	-1,53
23.11.2001	-2,60	0,43	0,90	0,16	3,17	-0,31	0,88	2,12	1,59	0,44	-1,06	0,62	-0,72	-1,14	5,21
26.11.2001	0,89	1,89	0,21	-2,16	-1,03	0,33	0,38	5,79	1,84	2,63	1,11	-0,19	2,22	2,44	1,76
27.11.2001	-0,44	0,32	1,15	-0,93	2,77	0,55	0,14	4,34	3,82	-0,45	-0,90	0,16	2,78	-1,70	2,09
28.11.2001	-1,77	-1,42	0,90	-1,92	2,04	-0,91	-1,31	1,92	-2,32	-1,64	-0,51	0,31	-2,43	-1,44	0,84
29.11.2001	2,25	-2,03	3,19	-2,66	4,28	-1,33	-1,82	-2,93	-1,36	-0,26	-0,53	-0,36	-2,02	0,21	-0,49
30.11.2001	0,00	5,27	0,25	3,79	5,20	0,54	0,59	5,36	-2,48	0,35	2,46	0,84	3,77	1,36	3,09
03.12.2001	1,76	-0,42	0,06	-0,07	-0,23	-0,93	-0,53	-0,31	-0,19	0,00	0,86	-0,49	-27,31	-0,71	0,36
04.12.2001	1,73	4,04	-5,74	3,37	7,57	0,18	3,06	2,04	0,57	1,04	3,34	3,76	42,98	2,94	-1,67
05.12.2001	1,28	0,59	5,12	1,44	2,33	0,48	3,71	-1,57	0,83	0,22	1,76	0,89	2,31	-0,46	-0,24
06.12.2001	-0,42	1,34	-0,29	1,75	9,59	1,27	2,10	-0,44	5,02	0,14	2,37	1,46	6,66	2,23	2,14
07.12.2001	1,27	-2,56	-0,20	-1,84	7,04	-1,02	-1,08	-0,90	-0,18	0,06	-0,70	-0,96	-2,34	0,05	-1,74
10.12.2001	0,42	0,76	0,72	1,40	12,87	-0,23	-0,34	-0,15	0,00	1,32	0,83	1,19	4,43	0,14	-0,30
11.12.2001	-1,24	0,52	-6,90	-0,48	-4,72	1,04	2,87	-0,53	2,27	-0,27	0,49	1,47	3,10	0,12	1,11
13.12.2001	-3,36	-4,73	1,02	-3,40	-3,03	-1,93	-4,24	-4,97	-0,63	-3,71	-3,09	-2,14	1,69	-1,94	-3,34
14.12.2001	0,43	-2,37	0,04	-3,80	-4,65	-2,70	-2,12	-2,58	-4,94	-0,37	-2,97	-0,91	-2,27	-1,20	0,08
17.12.2001	2,16	2,42	3,53	2,52	7,35	-0,47	0,76	4,12	-0,34	-0,04	2,45	1,11	3,60	1,24	1,67
18.12.2001	0,85	3,00	2,78	0,39	3,10	1,35	3,98	2,85	0,13	0,05	2,61	1,42	3,52	1,03	4,53
19.12.2001	2,10	1,96	0,88	0,75	7,53	0,62	0,52	1,16	4,23	1,03	1,46	4,40	0,55	1,03	1,75
20.12.2001	0,00	0,95	0,30	2,20	0,84	-0,64	0,64	0,92	1,87	0,84	1,30	2,28	0,65	2,97	3,60
21.12.2001	2,88	-0,31	-0,07	-0,43	-2,40	1,11	-0,10	2,07	-0,13	1,37	-0,03	0,94	3,98	-0,64	2,48
24.12.2001	0,40	3,03	1,35	2,84	2,36	1,93	4,76	2,75	0,05	1,98	3,87	1,62	1,98	4,74	6,27
25.12.2001	-0,40	-1,92	-1,86	-0,91	3,35	0,12	0,20	-2,23	0,06	3,59	-2,07	0,46	-3,59	-1,19	-0,16
26.12.2001	0,80	-0,15	0,06	-0,30	-0,53	-0,01	-0,59	-0,68	0,00	0,00	-0,28	1,00	0,88	-0,13	1,02
27.12.2001	1,59	1,13	2,15	0,78	1,87	0,07	1,50	0,30	-0,21	3,64	1,51	0,84	-0,97	2,53	0,00
28.12.2001	0,39	0,77	2,01	2,41	-1,44	1,94	0,07	0,16	0,30	0,68	1,44	1,08	1,24	2,21	-2,42
Продолжении таблицы Б.2	В %
Дата	РТС	EESR	GSPBEX	LKOH	SBER	TATN	MSNG	RTKM	GMKN	SIBN	SNGS	YUKO	EESRP	SNGSP	RTKMP
29.12.2001	1,95	0,42	0,29	0,59	2,88	0,49	0,00	0,09	0,41	0,04	0,76	-0,09	1,47	0,45	-0,09
03.01.2002	3,44	3,83	5,01	3,84	0,09	3,45	5,99	2,48	2,76	0,70	2,77	1,00	1,39	2,26	4,34
04.01.2002	4,06	6,25	4,89	3,06	3,63	8,09	4,74	4,03	4,30	0,69	4,26	2,32	4,80	1,63	0,30
08.01.2002	1,42	3,53	4,05	4,12	-1,82	7,30	3,13	6,87	6,01	11,77	4,52	3,76	2,83	4,49	5,09
09.01.2002	1,05	-0,65	-2,82	2,37	0,24	-0,24	-0,53	0,48	-2,30	4,25	0,66	1,64	3,24	1,05	-0,17
10.01.2002	-0,69	-2,36	-1,49	0,21	-2,59	-4,43	-3,84	-3,87	-3,08	-0,34	-0,97	0,69	-0,94	-0,76	-0,62
11.01.2002	-1,05	-0,04	0,66	0,66	1,59	-0,63	-0,71	0,30	0,00	0,63	0,06	4,51	-34,61	-0,57	0,91
14.01.2002	-2,11	-3,42	-2,58	-2,11	-1,56	-4,28	-3,71	-2,97	-4,54	-2,78	-2,76	-1,43	52,05	-3,01	-1,19
15.01.2002	1,80	-1,41	-0,85	-0,50	0,71	-0,47	3,27	-0,36	-3,06	0,00	-2,67	-0,88	-2,09	-2,56	-4,35
16.01.2002	0,00	1,55	1,53	0,61	8,60	1,13	1,92	1,61	0,62	0,91	0,11	2,62	-26,74	1,13	0,78
17.01.2002	3,18	1,05	0,14	2,56	5,27	-0,19	1,51	-0,11	-0,29	0,49	1,22	-0,38	41,46	1,67	0,77
18.01.2002	-0,34	-0,19	0,52	4,56	4,97	0,79	0,15	2,16	-1,24	1,40	0,40	-0,32	-1,14	-0,08	1,43
21.01.2002	0,69	-0,47	1,26	1,28	-1,72	2,00	-0,88	-0,40	-1,44	1,64	-0,10	1,21	0,84	-0,68	-0,11
22.01.2002	2,05	2,14	3,84	2,90	0,35	2,42	3,78	4,60	0,03	1,57	3,85	2,27	0,76	2,94	3,53
23.01.2002	-2,68	-0,16	0,95	0,72	-1,55	-0,83	0,84	2,23	-0,08	-0,18	-1,87	-0,92	0,75	-1,66	3,21
24.01.2002	-3,44	-3,34	-2,72	-3,82	-3,80	-7,78	-3,30	-1,55	-6,09	-2,36	-5,78	-3,75	-3,75	-3,91	-0,08
25.01.2002	-0,71	-3,60	-0,19	-4,20	-4,50	-5,70	-2,45	-1,49	-2,53	-3,07	-0,62	0,94	-4,91	-1,62	-1,67
28.01.2002	2,51	-0,89	0,15	-1,20	-1,73	-0,20	-2,67	-0,21	0,71	0,21	0,97	0,40	0,32	1,83	-2,38
29.01.2002	0,00	2,78	2,82	3,61	2,50	1,96	0,61	1,95	4,60	4,81	2,72	5,71	5,13	4,25	2,60
30.01.2002	0,35	-2,41	-1,71	-4,07	0,00	-3,00	-2,54	-2,78	-1,78	-0,45	-2,84	-2,08	-0,57	-3,23	-3,15
31.01.2002	1,05	1,90	1,06	1,50	2,13	0,25	0,99	0,47	1,44	-1,86	1,66	1,85	0,98	1,67	4,51
01.02.2002	-1,38	-2,45	-0,83	-0,72	1,04	2,02	2,03	3,02	4,47	0,52	0,03	2,52	-0,09	3,07	0,19
04.02.2002	-0,70	-4,13	-0,63	-2,21	-4,55	-1,74	-0,29	0,11	-0,46	-0,11	-0,45	1,96	0,56	1,49	-0,11
05.02.2002	1,76	-1,50	0,08	0,21	-0,65	-0,59	-2,83	-1,09	-1,32	0,33	-0,94	-0,46	-0,56	-1,21	-1,36
06.02.2002	0,69	2,60	0,79	2,37	1,87	1,24	-2,31	4,94	0,24	0,19	1,89	1,84	-0,12	0,78	4,86
07.02.2002	1,72	0,01	1,41	2,20	0,31	0,54	1,44	2,08	4,42	3,40	-0,02	0,32	-2,36	-0,86	0,63
08.02.2002	-0,68	0,14	1,17	-1,07	4,15	0,41	0,82	0,42	4,60	3,23	-0,88	0,23	-3,20	1,57	1,75
11.02.2002	1,70	-0,45	-0,39	0,18	-1,35	-0,11	-2,78	1,74	-1,08	2,34	0,18	-0,23	-2,02	0,81	3,40
12.02.2002	-1,00	0,05	-0,02	0,97	3,26	2,80	-0,98	1,01	0,11	8,72	2,81	0,17	-1,73	1,46	1,19
13.02.2002	-2,36	-1,37	-0,78	-2,19	0,57	-0,30	-1,90	-3,07	0,17	-4,17	-0,98	0,18	0,00	-0,85	-1,64
14.02.2002	2,42	-0,45	-0,53	-4,48	-1,17	0,97	-0,86	-1,06	-0,67	3,24	-0,51	-1,00	0,43	0,34	2,28
Продолжении таблицы Б.2	В %
Дата	РТС	EESR	GSPBEX	LKOH	SBER	TATN	MSNG	RTKM	GMKN	SIBN	SNGS	YUKO	EESRP	SNGSP	RTKMP
15.02.2002	0,34	0,66	-0,17	-0,92	2,02	2,51	-1,83	1,46	0,03	2,32	1,44	0,46	0,42	0,25	-1,01
18.02.2002	-2,36	-2,30	-0,71	-3,95	-2,30	-0,47	-0,55	-2,00	0,52	0,48	-0,46	0,19	-0,84	-1,14	-0,27
19.02.2002	-1,72	-1,56	1,31	-1,31	0,64	-3,51	-0,73	-0,46	2,43	0,17	-0,86	-0,22	5,96	0,33	0,56
20.02.2002	0,70	-2,46	0,01	-3,71	-0,26	-1,60	-4,77	-4,14	-0,93	-1,33	-3,14	-1,96	-9,64	-2,62	-2,10
21.02.2002	0,70	3,23	0,93	1,88	-0,90	1,96	1,55	-0,14	0,28	1,84	2,21	1,09	4,26	-0,62	0,09
22.02.2002	2,77	1,45	1,14	2,91	4,96	2,18	3,01	3,57	5,35	2,08	-0,05	2,80	13,39	-0,41	1,84
26.02.2002	-1,01	3,22	4,72	0,53	1,28	0,20	2,56	1,05	5,47	8,12	-1,46	2,04	-7,54	3,34	2,38
27.02.2002	-0,68	-1,70	1,77	-3,50	-0,86	-4,29	0,22	0,77	-1,91	-0,07	-4,98	-1,56	-3,23	-7,11	2,01
28.02.2002	1,03	-0,32	1,72	-1,90	-1,19	-0,99	-3,06	2,54	0,27	-0,21	-2,26	0,34	12,06	-1,18	-0,79
01.03.2002	8,81	4,14	6,73	2,54	3,63	0,27	4,98	0,22	2,78	7,22	4,40	5,57	-6,20	5,65	0,63
04.03.2002	-0,93	7,15	8,47	3,41	4,86	6,94	4,65	4,39	-0,22	18,20	5,96	8,14	4,73	2,88	2,52
05.03.2002	-0,31	-0,86	-0,48	0,19	-1,65	-0,03	-0,61	0,22	-0,35	-2,84	0,95	-2,25	-2,29	0,01	3,85
06.03.2002	1,26	-0,50	0,09	0,47	-2,29	-0,64	-0,68	-0,49	-1,46	-6,87	1,63	0,10	0,00	1,06	-2,22
07.03.2002	3,12	3,23	1,47	2,25	2,95	1,55	3,15	3,30	1,54	4,30	4,52	5,27	3,99	2,30	4,38
11.03.2002	-3,63	-2,33	-3,21	-1,40	2,19	5,18	-3,70	-1,23	1,23	3,64	0,49	-3,41	-2,07	0,96	5,24
12.03.2002	1,25	-3,84	-11,55	-1,90	-1,13	3,64	-2,31	-3,02	-0,97	-0,38	-2,25	-2,97	-2,19	-2,94	-3,41
13.03.2002	0,00	1,04	7,39	1,92	-0,77	1,15	-0,93	-0,95	0,49	0,34	2,09	0,27	1,76	-0,74	1,04
14.03.2002	4,33	1,80	4,25	-0,56	2,20	0,65	0,07	1,00	1,47	8,24	2,49	3,50	-0,58	3,04	0,62
15.03.2002	2,08	1,77	2,29	2,71	4,91	1,29	2,26	1,72	2,10	8,54	3,54	1,76	0,43	1,95	0,48
18.03.2002	0,87	1,04	0,10	3,60	6,08	2,49	2,00	2,76	2,48	3,79	2,05	2,39	1,51	2,53	1,62
19.03.2002	0,00	-1,78	-3,98	-1,47	-2,10	-1,07	3,80	0,12	1,44	0,13	1,04	1,96	-4,18	-2,28	-3,43
20.03.2002	-2,31	-2,26	-1,60	-1,99	-0,42	-3,92	-0,05	-3,29	-0,19	-0,38	-1,55	-0,76	-2,78	-1,97	-2,13
21.03.2002	1,77	0,56	-0,78	0,88	3,26	0,28	-1,16	1,41	-0,81	-1,01	-0,02	-1,99	2,86	0,54	1,89
22.03.2002	0,87	0,01	-0,03	2,44	9,59	4,43	0,32	0,58	0,91	0,00	1,63	0,05	-4,76	0,69	0,71
25.03.2002	-4,02	-1,90	-2,57	-1,13	0,29	3,84	-3,58	-0,27	1,77	-2,09	-0,34	-2,58	5,83	-1,72	-4,26
26.03.2002	1,20	-3,05	-0,74	-3,53	0,79	3,03	-3,38	0,12	-0,29	-7,31	-2,70	-2,25	-1,61	-0,65	2,59
27.03.2002	1,48	1,52	1,53	5,00	5,10	0,99	1,97	2,12	-1,37	-0,26	-2,63	3,84	-0,77	-1,14	1,80
28.03.2002	2,33	2,01	0,93	3,66	7,61	3,23	2,05	0,09	-0,58	4,81	-2,34	3,85	-5,24	-1,42	0,71
29.03.2002	-0,28	1,35	2,74	1,58	-1,21	-1,05	0,78	0,97	0,95	3,31	2,28	1,82	-0,94	-0,11	-0,07
01.04.2002	-0,29	-0,95	-0,84	-0,38	1,23	-0,65	-0,56	-1,09	-0,07	-0,77	-0,39	-0,21	5,67	-0,80	-0,63

Приложение Г

Данные для определения динамики стоимости сформированного портфеля

Таблица Г.1 – Доходность к погашению ОФЗ за апрель 2002г. В % годовых

Дата	ОФЗ 26001	ОФЗ 27004	ОФЗ 27005	ОФЗ 27007	ОФЗ 27008	ОФЗ 27009	ОФЗ 27010	ОФЗ 27012	Портфель
01.04.2002	15,54	15,06	14,23	15,70	15,98	16,01	16,20	16,19	15,78
02.04.2002	15,32	15,49	15,92	16,20	16,56	16,55	16,51	16,30	16,08
03.04.2002	15,07	14,99	15,00	15,76	15,88	16,25	16,28	16,41	15,92
04.04.2002	14,92	14,34	14,83	16,30	15,89	15,95	15,98	16,63	15,97
05.04.2002	14,94	14,49	14,94	15,85	15,96	16,20	15,85	16,41	15,87
08.04.2002	15,48	14,80	14,96	15,90	15,88	16,10	16,34	16,77	16,18
09.04.2002	15,50	14,68	14,42	15,76	16,03	16,11	16,38	16,71	16,08
10.04.2002	15,51	14,64	14,36	15,81	16,24	15,97	16,22	16,60	16,01
11.04.2002	15,52	14,61	13,69	15,55	15,87	15,85	16,04	16,50	15,84
12.04.2002	15,54	14,68	13,93	14,58	15,76	15,77	16,04	16,50	15,85
15.04.2002	15,58	14,44	14,75	15,60	15,88	15,63	16,19	16,43	15,94
16.04.2002	15,59	14,65	14,50	15,59	15,92	15,79	16,10	16,51	15,97
17.04.2002	15,61	14,67	14,25	15,54	15,82	15,84	16,09	16,30	15,82
18.04.2002	15,62	14,34	14,45	15,54	15,83	15,85	15,97	16,43	15,91
19.04.2002	15,64	15,27	15,10	15,60	15,99	15,99	16,29	16,54	16,10
22.04.2002	15,68	15,19	14,35	15,93	16,16	16,03	16,02	16,48	15,98
23.04.2002	15,70	15,19	15,17	15,68	16,06	15,85	16,04	16,42	16,04
24.04.2002	15,71	15,20	14,62	15,83	15,84	15,72	15,97	16,41	15,96
25.04.2002	15,73	14,96	14,25	15,58	15,83	15,67	15,88	16,43	15,91
26.04.2002	15,74	15,00	14,73	15,61	15,53	15,44	15,87	16,27	15,87
27.04.2002	15,76	15,02	14,82	15,50	15,44	14,98	15,91	16,35	15,90
29.04.2002	15,79	14,75	14,80	15,41	15,22	15,49	15,87	16,23	15,85
30.04.2002	15,81	14,33	14,86	15,38	15,26	15,50	15,68	16,31	15,89

Таблица Г.2 – Стоимость ОФЗ за апрель 2002г. В рублях

Дата	ОФЗ 26001	ОФЗ 27004	ОФЗ 27005	ОФЗ 27007	ОФЗ 27008	ОФЗ 27009	ОФЗ 27010	ОФЗ 27012	Портфель
01.04.2002	953,8	10,023	9,895	9,779	9,657	9,666	9,536	9,176	2322523
02.04.2002	953,8	10,010	9,917	9,779	9,654	9,658	9,500	9,171	2322034
03.04.2002	953,8	10,024	9,919	9,775	9,656	9,632	9,516	9,167	2321434
04.04.2002	953,8	10,053	9,921	9,743	9,660	9,657	9,557	9,165	2321723
05.04.2002	953,8	10,041	9,920	9,767	9,656	9,639	9,566	9,169	2322199
08.04.2002	954,4	10,030	9,921	9,765	9,665	9,650	9,513	9,158	2320713
09.04.2002	955,1	10,039	9,938	9,773	9,645	9,646	9,513	9,164	2322245
10.04.2002	955,1	10,034	9,944	9,770	9,632	9,659	9,524	9,180	2324707
11.04.2002	955,1	10,039	9,977	9,789	9,667	9,664	9,548	9,187	2327225
12.04.2002	955,1	10,040	9,965	9,807	9,672	9,660	9,552	9,194	2327991
15.04.2002	955,1	10,040	9,927	9,825	9,672	9,690	9,527	9,206	2328807
16.04.2002	955,1	10,036	9,941	9,787	9,664	9,683	9,542	9,201	2328242
17.04.2002	955,1	10,039	9,941	9,794	9,666	9,680	9,541	9,201	2328274
18.04.2002	955,1	10,045	9,942	9,781	9,669	9,672	9,553	9,203	2328548
19.04.2002	955,1	10,016	9,942	9,790	9,665	9,662	9,523	9,203	2328132
22.04.2002	955,1	10,020	9,938	9,777	9,637	9,652	9,535	9,209	2328567
23.04.2002	955,1	10,014	9,910	9,780	9,650	9,662	9,545	9,220	2329555
24.04.2002	955,1	10,018	9,926	9,775	9,663	9,677	9,556	9,225	2331013
25.04.2002	956,3	10,020	9,944	9,785	9,667	9,886	9,560	9,218	2333404
26.04.2002	955,0	10,022	9,919	9,787	9,697	9,699	9,565	9,219	2330569
27.04.2002	955,0	10,026	9,917	9,788	9,698	9,711	9,565	9,237	2333149
29.04.2002	955,0	10,028	9,917	9,799	9,702	9,714	9,566	9,250	2335086
30.04.2002	955,0	10,032	9,919	9,798	9,702	9,714	9,566	9,251	2335291

Таблица Г.3 – Цены акций за апрель 2002г. В рублях

Дата	EESRP	RTKMP	SBER	SIBN	RTKM	YUKO	EESR	LKOH	SNGSP	TATN	Портфель
01.04.2002	3,828	21,939	4295,9	52,021	39,102	258,53	5,051	453,60	6,784	21,204	2718393
02.04.2002	3,840	21,588	4370,6	51,603	39,088	262,09	4,988	453,28	6,762	20,465	2726167
03.04.2002	3,671	21,541	4291,1	49,786	38,017	257,56	4,825	437,08	6,570	20,371	2671066
04.04.2002	3,662	21,620	4331,4	50,533	37,502	259,25	4,820	441,46	6,457	19,914	2681157
05.04.2002	3,649	21,451	4609,6	49,894	37,536	259,35	4,842	449,03	6,512	20,016	2710904
08.04.2002	3,656	21,313	4685,4	49,608	37,760	264,07	4,789	452,43	6,590	20,178	2731837
09.04.2002	3,745	22,095	4752,1	51,846	38,910	278,43	4,963	468,19	6,772	20,772	2832465
10.04.2002	3,787	22,229	5006,1	52,855	40,143	289,76	5,045	472,45	6,747	20,812	2920888
11.04.2002	3,902	23,843	5018,0	53,353	44,184	289,17	5,086	483,43	6,655	21,152	2997788
12.04.2002	4,085	22,843	4835,1	52,651	43,519	294,71	5,018	482,61	6,645	21,144	2963032
15.04.2002	4,200	23,598	4753,9	52,544	44,224	299,87	5,063	501,58	6,760	21,260	2996913
16.04.2002	4,081	23,613	4753,8	55,459	46,143	301,07	5,205	507,37	6,725	21,451	3038576
17.04.2002	4,155	24,053	4997,8	55,298	46,697	301,22	5,193	509,80	6,728	21,705	3082577
18.04.2002	4,227	25,172	5163,6	58,129	49,795	310,34	5,281	530,62	6,833	22,398	3205096
19.04.2002	4,297	26,135	5169,9	58,890	51,053	300,37	5,134	530,10	6,837	23,603	3207584
22.04.2002	4,203	26,177	5174,4	57,242	50,740	295,60	4,991	535,47	6,771	23,718	3178087
23.04.2002	4,177	26,043	5243,5	55,925	51,138	295,05	4,926	532,56	6,716	23,505	3175611
24.04.2002	4,112	26,182	5289,5	56,875	51,597	299,86	4,982	535,23	6,726	24,495	3210493
25.04.2002	4,051	25,438	5436,5	56,580	49,597	299,37	4,934	539,36	6,792	24,986	3190950
26.04.2002	4,063	24,475	5424,4	56,861	48,251	306,09	4,882	553,51	6,966	26,272	3183211
27.04.2002	4,102	23,922	5381,6	57,936	47,744	305,05	4,885	558,39	6,985	26,403	3166648
29.04.2002	4,049	23,751	5428,9	57,809	47,951	306,23	4,903	564,14	6,932	26,487	3174838
30.04.2002	3,931	23,553	5330,0	57,635	46,220	305,41	4,715	556,48	6,972	25,458	3129325

Таблица В.2– Курс доллара США, установленный ЦБ РФ В рублях

Число	2001 год	2002 год
Октябрь	Ноябрь	Декабрь	Январь	Февраль	Март	Апрель
1	29,3900	29,6800	29,9000	30,1372	30,6797	30,9404	31,1192
2	29,4300	29,7000	29,9000	30,1372	30,6827	30,9436	31,1741
3	29,4500	29,7300	29,9000	30,1372	30,6827	30,9436	31,1733
4	29,4800	29,7300	29,9300	30,1372	30,6827	30,9436	31,1933
5	29,5000	29,7300	29,9300	30,1372	30,7299	30,9949	31,1840
6	29,5200	29,7400	29,9400	30,1372	30,7246	30,9909	31,1820
7	29,5200	29,6800	29,9200	30,1372	30,7318	30,9946	31,1820
8	29,5200	29,6800	29,9500	30,1372	30,7236	30,9946	31,1820
9	29,5200	29,6800	29,9500	30,1372	30,7644	30,9946	31,1893
10	29,5200	29,7100	29,9500	30,5753	30,7644	30,9946	31,1644
11	29,5000	29,7100	30,0900	30,4999	30,7644	30,9946	31,1679
12	29,5300	29,7100	30,0800	30,4399	30,8163	31,0632	31,1982
13	29,5000	29,7100	30,1900	30,4399	30,8421	31,0545	31,1734
14	29,5000	29,7200	30,1800	30,4399	30,8438	31,0758	31,1734
15	29,5000	29,7200	30,1800	30,4491	30,8281	31,0237	31,1734
16	29,5100	29,7600	30,1800	30,4751	30,8206	31,0710	31,1522
17	29,4900	29,7800	30,1800	30,4778	30,8206	31,0710	31,1498
18	29,5400	29,7800	30,3000	30,5798	30,8206	31,0710	31,1517
19	29,5500	29,7800	30,2800	30,5788	30,8206	31,1119	31,1649
20	29,5500	29,8000	30,2800	30,5788	30,8949	31,1248	31,1711
21	29,5500	29,9100	30,2600	30,5788	30,8840	31,1325	31,1711
22	29,5500	29,9000	30,0800	30,5788	30,8580	31,1276	31,1711
23	29,5400	29,9000	30,0800	30,5572	30,8409	31,1168	31,1516
24	29,5400	29,9300	30,0800	30,5596	30,8409	31,1168	31,1498
25	29,5700	29,9300	30,1200	30,5380	30,8409	31,1168	31,1579
26	29,5900	29,9300	30,1200	30,5949	30,8409	31,1510	31,1783
27	29,6300	29,9300	30,2100	30,5949	30,8949	31,1353	31,1977
28	29,6300	29,9300	30,1400	30,5949	30,9274	31,1147	31,1977
29	29,6300	29,9300	30,1400	30,6623	—	31,0686	31,1977
30	29,6800	29,9000	30,1400	30,6540	—	31,1192	31,1963
31	29,7000	—	30,1400	30,6850	—	31,1192	—

Приложение А

Исходные данные для формирования портфеля государственных облигаций

Таблица А.1 – Список торгуемых инструментов на государственном секторе ММВБ на 01.04.2002

Наименование ценной бумаги	Вид ценной бумаги	Номинал (руб.)	Дата размещения	Дата погашения	Объявленный объем (шт.)
ГКО 21156	ГКО	1000	28.11.2001	17.07.2002	6 000 000
ГКО 21157	ГКО	1000	30.01.2002	07.08.2002	4 000 000
ГКО 21158	ГКО	1000	20.02.2002	21.08.2002	6 000 000
ГКО 21159	ГКО	1000	13.03.2002	06.11.2002	6 000 000
ОФЗ 25028	ОФЗ-ПД	1000	27.11.1998	27.11.2002	163 722
ОФЗ 25029	ОФЗ-ПД	1000	27.11.1998	27.11.2003	163 722
ОФЗ 25053	ОФЗ-ПД	1000	26.12.2000	21.11.2005	5 036
ОФЗ 26001	ОФЗ-ПД	1000	15.03.1997	15.03.2003	6 142 000
ОФЗ 26002	ОФЗ-ПД	1000	15.03.1997	15.03.2004	6 142 000
ОФЗ 26003	ОФЗ-ПД	1000	15.03.1997	15.03.2005	6 142 000
ОФЗ 26032	ОФЗ-ПД	1000	27.11.1998	27.11.2004	163 722
ОФЗ 26175	ОФЗ-ПД	1000	26.12.2000	20.11.2006	5 036
ОФЗ 26176	ОФЗ-ПД	1000	26.12.2000	20.11.2007	5 036
ОФЗ 26177	ОФЗ-ПД	1000	26.12.2000	20.11.2008	5 036
ОФЗ 26178	ОФЗ-ПД	1000	26.12.2000	20.11.2009	5 036
ОФЗ 27002	ОФЗ-ФД	10	19.08.1998	22.05.2002	1 000 000 000
ОФЗ 27003	ОФЗ-ФД	10	19.08.1998	05.06.2002	1 000 000 000
ОФЗ 27004	ОФЗ-ФД	10	19.08.1998	18.09.2002	1 000 000 000
ОФЗ 27005	ОФЗ-ФД	10	19.08.1998	09.10.2002	1 000 000 000
ОФЗ 27006	ОФЗ-ФД	10	19.08.1998	22.01.2003	1 000 000 000
ОФЗ 27007	ОФЗ-ФД	10	19.08.1998	05.02.2003	1 000 000 000
ОФЗ 27008	ОФЗ-ФД	10	19.08.1998	21.05.2003	1 000 000 000
ОФЗ 27009	ОФЗ-ФД	10	19.08.1998	04.06.2003	1 000 000 000
ОФЗ 27010	ОФЗ-ФД	10	19.08.1998	17.09.2003	1 000 000 000
ОФЗ 27011	ОФЗ-ФД	10	19.08.1998	08.10.2003	1 000 000 000
ОФЗ 27012	ОФЗ-ФД	10	01.02.2000	19.11.2003	1 760 640 000
ОФЗ 27013	ОФЗ-ФД	1000	06.06.2001	02.06.2004	5 000 000
ОФЗ 27014	ОФЗ-ФД	1000	11.07.2001	15.12.2004	5 000 000
ОФЗ 27015	ОФЗ-ФД	1000	08.08.2001	04.02.2004	5 000 000
ОФЗ 27016	ОФЗ-ФД	1000	21.11.2001	20.08.2003	12 000 000
ОФЗ 27017	ОФЗ-ПК	1000	06.02.2002	04.08.2004	7 000 000
ОФЗ 27018	ОФЗ-ФД	1000	20.03.2002	14.09.2005	9 000 000
ОФЗ 28001	ОФЗ-ФД	10	19.08.1998	21.01.2004	1 000 000 000
ОФЗ 29004	ОФЗ-ПК	1000	29.12.2000	10.05.2017	4 819 896

Приложение В

Вспомогательные данные для формирования совокупного портфеля ценных бумаг

Таблица В.1 – Доходности ценных бумаг для совокупного портфеля

Период расчета доходности	Доходность портфеля, % в месяц
Облигации	Акции
01.10.2001 – 08.10.2001	1,398	-3,037
08.10.2001 – 15.10.2001	1,402	22,062
15.10.2001 – 22.10.2001	1,391	14,675
22.10.2001 – 29.10.2001	1,379	10,663
29.10.2001 –05.11.2001	1,364	13,099
05.11.2001 – 12.11.2001	1,491	28,171
12.11.2001 – 19.11.2001	1,364	-9,563
19.11.2001 – 26.11.2001	1,370	44,313
26.11.2001 – 03.12.2001	1,370	48,090
03.12.2001 – 10.12.2001	1,359	157,640
10.12.2001 – 17.12.2001	1,359	-17,015
17.12.2001 – 24.12.2001	1,383	43,203
24.12.2001 – 08.01.2002	1,315	41,557
08.01.2002 – 14.01.2002	1,285	-8,199
14.01.2002 – 21.01.2002	1,270	68,294
21.01.2002 – 28.01.2002	1,263	-37,668
28.01.2002 – 04.02.2002	1,228	8,179
04.02.2002 – 11.02.2002	1,205	17,573
11.02.2002 – 18.02.2002	1,218	7,818
18.02.2002 – 26.02.2002	1,228	21,757
26.02.2002 – 04.03.2002	1,300	29,672
04.03.2002 – 11.03.2002	1,258	4,784
11.03.2002 – 18.03.2002	1,341	43,479
18.03.2002 – 25.03.2002	1,374	35,604
25.03.2002 – 01.04.2002	1,330	52,499

Таблица В.3 – Данные для построения эффективного множества

Доля инвестиций в	Математическое ожидание доходности, % в месяц	Риск портфеля
портфель облигаций	портфель акций
0	1	26,6	1354,4
0,05	0,95	25,3	1222,4
0,10	0,90	24,1	1097,1
0,15	0,85	22,8	978,7
0,20	0,80	21,5	866,9
0,25	0,75	20,3	762,0
0,30	0,70	19,0	663,8
0,35	0,65	17,8	572,4
0,40	0,60	16,5	487,8
0,45	0,55	15,2	409,9
0,50	0,50	14,0	338,8
0,55	0,45	12,7	274,5
0,60	0,40	11,4	216,9
0,65	0,35	10,2	166,1
0,70	0,30	8,9	122,1
0,75	0,25	7,7	84,8
0,80	0,20	6,4	54,3
0,85	0,15	5,1	30,6
0,90	0,10	3,9	13,6
0,95	0,05	2,6	3,4
1	0	1,3	0,0

Приложение Д

Графики цен закрытия акций (РТС) на период составления портфеля

Рисунок Д.1 – Динамика индекса РТС на момент закрытия

Рисунок Д.2 – Динамика цен закрытия акций EESR

Рисунок Д.3 – Динамика цен закрытия акций EESRP

Рисунок Д.4 – Динамика цен закрытия акций GMKN

Рисунок Д.5 – Динамика цен закрытия акций LKOH

Рисунок Д.6 – Динамика цен закрытия акций SIBN

Рисунок Д.7 – Динамика цен закрытия акций RTKM

Рисунок Д.8 – Динамика цен закрытия акций RTRMP

Рисунок Д.9 – Динамика цен закрытия акций SNGS

Рисунок Д.10 – Динамика цен закрытия акций SNGSP

Рисунок Д.11 – Динамика цен закрытия акций TATN

Рисунок Д.12 – Динамика цен закрытия акции YUKO

Рисунок Д.13 – Динамика цен закрытия акций MSNG

ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Факультет “Экономика и управление”__

Кафедра “Экономика и финансы”___

ПРОЕКТ ПРОВЕРЕН

Рецензент

“ _____ ” _____________ 2002 г.

ДОПУСТИТЬ К ЗАЩИТЕ

Заведующий кафедрой

Баев И.А.

“ _____ ” _____________ 2002 г.

Формирование портфеля ценных бумаг коммерческого банка

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К ДИПЛОМНОМУ ПРОЕКТУ

ЮУрГУ-Д

Консультанты:

БЖД

Степанова М.В.

“ _____ ” ______________ 2002 г.

“ _____ ” ______________ 2002 г.

“ _____ ” ______________ 2002 г.

“ _____ ” ______________ 2002 г.

000 ПЗ

Руководитель проекта:

Дягелец И.Д.

Автор проекта
студент группы ЭиУ-563

Величко О.С.

Нормоконтролер

Матвеева Н.И.

“ _____ ” ______________ 2002 г.

Челябинск 2002 г.

ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Факультет __”Экономика и управление” __________________________________

Специальность _”Финансы и кредит”_____________________________________

УТВЕРЖДАЮ:

Зав.кафедрой

Баев И.А.____________

“ ____ ” _________ 2002 г.

З А Д А Н И Е

по дипломному проекту (работе) студента

Величко Оксана Сергеевна

(фамилия, имя, отчество)

1. Тема проекта (работы) __________________________________________________

Формирование портфеля ценных бумаг коммерческого банка

утверждена приказом по университету от “ 30_” апреля_ 2002 г. № __1615______________

2. Срок сдачи студентом законченного проекта (работы) 30.05.2002__________________

3. Исходные данные к проекту (работе) _______________________________________________

Специальная методическая и справочная литература по исследуемой проблеме

Биржевые котировки ценных бумаг

Данные преддипломной практики

Система связи Интернет

4. Содержание расчетно-пояснительной записки (перечень подлежащих разработке вопросов)

1   Портфельное инвестирование

2   Методики формирования оптимальной структуры портфеля

3   Формирование и оптимизация портфеля ценных бумаг 

(на примере АБ «Дорожник»)

3.1   Формирование оптимальной структуры портфеля государственных бумаг

3.2   Формирование оптимальной структуры портфеля акций

3.3   Формирование оптимальной структуры совокупного портфеля

3.4   Анализ результатов практического расчета

4   Безопасность жизнедеятельности

5. Перечень графического материала (с точным указанием обязательных чертежей)

Цели инвестирования

Классификация портфелей в зависимости от источника дохода

Эффективное множество

Рыночная линия. Уравнение индексной модели Шарпа

Структура оптимального портфеля государственных облигаций

Бета-коэффициенты акций

Структура оптимального портфеля акций

Результаты формирования портфеля

Динамика доходности к погашению портфеля государственных облигаций

Динамика стоимости совокупного портфеля

6 Консультанты по проекту (работе), с указанием относящихся к ним разделов проекта:

Раздел	Консультант	Подпись, дата
задание выдал	задание принял
БЖД	Степанова М.В.

7. Дата выдачи задания 11.02.2002_________________________________________

Руководитель Дягелец И.Д._______________________________________

Задание принял к исполнению Величко О.С.______________________________________

К А Л Е Н Д А Р Н Ы Й П Л А Н

№ п/п	Наименование этапов дипломного проекта (работы)	Срок выполнения этапов проекта (работы)	Отметка о выполнении
1	Обзор литературных источников	11.02.02 – 01.04.02
2	Сбор данных при преддипломной практике	18.02.02 – 18.03.02
3	Сбор исходных данных из Интернета	25.03.02 – 01.04.02
4	Проведение расчетов	01.04.02 – 20.04.02
5	Оформление пояснительной записки	15.04.02 – 20.05.02
6	Разработка раздела БДЖ	15.05.02
7	Оформление графической части	27.05.02 – 28.05.02

Зав.кафедрой ______________________________________ / Баев И.А.____ /

Руководитель проекта ______________________________ / Дягелец И.Д.___ /

Студент-дипломник ________________________________ / Величко О.С.___ /