Модель Хольта-Уинтерса

Федеральное агентство по образованию

ГУ ВПО

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ

ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Кафедра математика и информатика

КОНТРОЛЬНАЯ РАБОТА

Дисциплина: Финансовая математика

вариант № 3

Выполнил студент

Группа № 4ф2ДО

Студенческий билет №06ДФД50396

Проверил: Копылов Юрий Николаевич

Барнаул 2008г

СОДЕРЖАНИЕ

Задача №1

Задача №2

Задача №3

Задача №1

Приведены по квартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года.

1	31
2	40
3	47
4	31
5	34
6	44
7	54
8	33
9	37
10	48
11	57
12	35
13	42
14	52
15	62
16	39

Требуется:

Построить адаптивную мультипликативную модель Хольта – Уинтерса с учетом сезонного фактора, приняв параметры сглаживания а1=0,3, а2=0,6, а3=0,3

Оценить точность построенной модели с использованием средней относительной ошибке аппроксимации.

Оценить адекватность построенной модели с использованием средней относительной по критерию типов:

- независимости уровней ряда остатков по d-критерию (критические значения d1=1.10, d2=1.37, и по первому коэффициенту автокорреляции при критическом значении r=0.32

- нормальности распределения остаточной компоненты по R/S критерию с критическими значениями от 3 до 4,21

4) Построить точечный прогноз на 4 шага вперед т.е. на 1 год

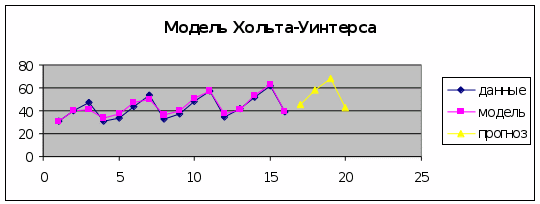
5) Отразить на графике фактические и расчетные данные.

Решение:

t	Y(t)	Yp(t)
1	31	36,00
2	40	36,93
3	47	37,86
4	31	38,79
5	34	39,71
6	44	40,64
7	54	41,57
8	33	42,50

линейнная	b(0)	a(0)
0,9286	35,0714

a1	0,3
aF	0,6
a3	0,3

t	Y(t)	a(t)	b(t)	F(t)	Yp(t)	e(t) =Y-Yp	e(t) ^2	пов. Точки
-3				0,859
-2				1,083
-1				1,049
0		35,071	0,929	0,788
1	31	36,310	1,022	0,856	30,91	0,09	0,01	0
2	40	37,520	1,078	1,073	40,43	-0,43	0,18	1
3	47	40,786	1,734	1,111	40,48	6,52	42,48	1
4	31	42,089	1,605	0,757	33,50	-2,50	6,25	0
5	34	42,987	1,393	0,817	37,39	-3,39	11,48	0
6	44	43,788	1,215	1,032	47,61	-3,61	13,04	1
7	54	46,449	1,649	1,142	50,00	4,00	16,03	1
8	33	47,240	1,392	0,722	36,41	-3,41	11,65	1
9	37	48,049	1,217	0,789	39,72	-2,72	7,42	0
10	48	48,804	1,078	1,003	50,84	-2,84	8,09	1
11	57	50,216	1,178	1,138	56,96	0,04	0,00	1
12	35	50,873	1,022	0,702	37,10	-2,10	4,43	1
13	42	52,608	1,236	0,795	40,93	1,07	1,14	1
14	52	53,616	1,167	0,983	54,00	-2,00	4,00	1
15	62	55,045	1,246	1,131	62,33	-0,33	0,11	1
16	39	56,455	1,295	0,695	39,49	-0,49	0,24	0
Сумма						126,57	11
среднее					-0,758

(et-et-1) ^2	et*et-1	модуль(e(t) /Y(t)) *100
0,01	0,000	0,290
0,27	-0,038	1,065
48,21	-2,776	13,868
81,33	-16,297	8,066
0,79	8,473	9,966
0,05	12,238	8, 208
57,99	-14,460	7,415
55,02	-13,669	10,345
0,48	9,302	7,364
0,01	7,748	5,924
8,31	-0,110	0,068
4,60	-0,082	6,014
10,06	-2,245	2,540
9,41	-2,134	3,848
2,78	0,667	0,538
0,03	0,164	1,263
279,34	-13,221
		5,42

Получили что средняя ошибка аппроксимации равна 5,42 - меньше 15%, то есть точность модели удовлетворительная

Se=

2,905

Критерий Поворотных точек

p=11

критическое по формуле

6

Поскольку число поворотных точек больше критического то критерий поворотных точек выполняется

3) критерий Дарбина – Уотсона

d=	2,21
d1=	1,10
d2=	1,37

варианты

1) если d меньше d1 - критерий не выполняется

2) если d больше d1 и меньше d2 - рассчитываем r1

3) если d больше d2, но меньше 2 - критерий выполняется

4) если d больше 2, то вычисляем 4-d и его проверяем

4-d=4-2,21=1,79

так как 1,10<1,79<1,37, то условие независимости ряда остатков выполняется.

Применим 2 вариант критерия, расчитываем r1

В таб доп. Колонка для расчета r1 с названием et*et-1

r1 =	-0,10
r таб=	0,32

вывод поскольку r1<r таб, то уровни ряда остатков являются независимыми

4) R/S критерий

e min	e max
-3,61	6,52

Так как 3<3,49<4,21, то уровни остатков подчиняются нормальному распределению.

ОБЩИЙ ВЫВОД: модель адекватна и подходит для расчета прогнозных значений

Прогноз
17	45,88351001
18	58,04633626
19	68,24039581
20	42,84375034

Задача №2

Даны цены (открытия максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным 5 дням.

Рассчитать:

- экономическую скользящую среднюю;

- момент;

- скорость из изменения цен;

- индекс относительной силы;

-%R,%K и%D

Дни	Цены
максимальная	минимальная	Закрытия
1 2 3 4 5 6 7 8 9 10	735 750 745 725 738 747 835 875 853 820	701 715 715 707 702 716 755 812 821 760	715 738 720 712 723 744 835 827 838 767

Решение:

n=5 – интервал сглаживания

Подставляя данные в эти формулы получаем

T	H(t)	L(t)	C(t)	EMA(t)	MOM	ROC	Изменения Ci
1	735	701	715
2	750	715	738				23
3	745	715	720				-18
4	725	707	712				-8
5	738	702	723	721,60			11
6	747	716	744	729,06	29	104,06	21
7	835	755	835	764,34	97	113,14	91
8	875	812	827	785, 20	107	114,86	-8
9	853	821	838	802,79	126	117,70	11
10	820	760	767	790,87	44	106,09	-71

повышение	понижение	AU	AD	RSI
23	0
0	18
0	8
11	0
21	0	55	26	67,90
91	0	123	26	82,55
0	8	123	16	88,49
11	0	134	8	94,37
0	71	123	79	60,89

H5	L5	H5-L5	Ct-L5	%K	H5-Ct	%R	%D
750	701	49	22	44,90	27	55,10
750	702	48	42	87,50	6	12,50
835	702	133	133	100,00	0	0,00	85,65
875	702	173	125	72,25	48	27,75	84,75
875	702	173	136	78,61	37	21,39	82,25
875	716	159	51	32,08	108	67,92	61,78

Общий вывод по этому показателю: в 10 день кривые сблизились, причем дневная сверху - приготовится к продаже, но поскольку имеются колебания в последние дни нужно быть осторожным

Вывод: у нас в 6,7 день ниже 100 - снижение цены, предпочтительнее продажа 8,9 - повышение цены, покупка, а в 10 день - продажа так как ниже 100%

Вывод: у нас все значения выше 100 - повышение цены, предпочтительнее покупка.

Вывод: 6 день выходит из зоны - покупка, 7,8,9 день - подготовится к продаже, 10 день выходит из зоны – покупать

По линии K%:

В 5 день критерий находится в зоне перепроданности подготовится к покупке, в 6,7 находится в зоне перекупленности подготовится к продаже на 8,9 день выходит из зоны перекупленности покупке; 10 день показывает что надо покупать.

По линии R%:

В 5 день вышел из зоны перепроданности надо покупать, 6.7.9. - (в зоне перепроданности) - подготовиться к покупке, 10 день вышел из зоны надо покупать.

По линии D%:

10 день показал что нужно покупать

Задача №3

Сумма	Дата начальная	Дата конечная	Время в днях	Время в годах	Ставка	Число начислений
S	TH	TK	Тдн	Тлет	i	m
1500000	17,01,02	13,03,02	180	4	20	2

Найти:

3.1.1. Точные проценты с точным числом дней ссуды;

3.1.2. Обыкновенные проценты с точным числом дней ссуды.

3.1.3. Обыкновенные проценты с приближенным числом дней ссуды

Решение:

3,1)	сумма процентов
S-сумма кредита
i-ставка за кредит
n - количество периодов начисления (поскольку проценты годовые, то n = t /K)
t - срок в днях
K - число дней в году

а) вычислить точные проценты с точным числом дней ссуды

K=	365
S=	1500000
i=	20
t=	56
сумма процентов	46027,40

б) вычислить обыкновенные проценты с точным числом дней

К=	360
S=	1500000
i=	20
t=	56
сумма процентов	46666,67

в) вычислить обыкновенные проценты с приближенным числом дней

число месяца когда взял	число месяца когда отдал	разница
17	13	4

t=

55

K=	360
t=	55
S=	1500000
i=	20
сумма процентов	45833,33

3.2) Через Тдн дней подписания договора должник уплатит S рублей. Кредит выдан под i% годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт

Решение:

Дисконт – разница между тем, что он отдал и тем, что взял – фактически – это сумму начисленных процентов.

Первоначальная сумма=	136 364
через Тдн=	180
должник уплатит S=	1500000
процентная ставка i=	20
K=	360
дисконт =	1 363 636

3.3) Через Тдн предприятие должно получить по векселю S руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке i% годовых (год равен 360 дней). Определить полученную сумму и дисконт?

Дисконт=	150000
t=Тдн=	180
K=	360
S=	1500000
d=i=	20
P=	1350000

3.4) В кредитном договоре на сумму S руб. и сроком на Тлет, зафиксирована ставка сложных процентов, равная i% годовых. Определить наращенную сумму?

P=	15694117,03
n=Тлет=	4
i=	20
S=	1500000
множ. Наращивания=	11,46

3.5) Ссуда, размером S руб. и предназначена сроком на Т лет. Проценты сложные, ставка i% годовых. Проценты начисляются m раз в году. Вычислить наращиваемую сумму?

S=	1500000
n=Tлет=	4
m=	2
%i=	20%
P=	3215383,215

3.6) Вычислить эффективную ставку процента если банк начисляет проценты m раз в году, исходя из номинальной ставки i% годовых

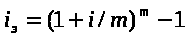
m=	2
%i=	20%
Iэ=	21,55%

0,21550625

21,55063

3.7) Определить какой должна быть номинальная ставка при начислении процентов m раз в году, чтобы обеспечить эффективную ставку i% годовых.

m=	2
iэ=	20%
i=	38,2%

0,38178046

38,17805

3.8) Через Тлет предприятию будет выплачена сумма S руб. Опрделить ее современную стоимость при условии, что применяется сложная ставка i% годовых?

S=	1500000
n=Tлет=	4
%i=	20%
P=	602816,36

3.9) Через Тлет по векселю должна быть выплачена сумма S руб. Банк учел вексель по сложной учетной ставке i% годовых. Определить дисконт?

S=	1500000
n=Tлет=	4
%i=	20%
современная сумма=	614400,00
Дисконт=	885600,00

3.10) В течении Тлет на расчетный счет в конце каждого года поступает по S руб., на которые m раз в году начисляются проценты по сложной годовой ставке i%. Определить сумму на расчетном счете к концу указанного периода?

S=	1500000
n=Tлет=	4
%i=	20%
m=	2
R=	24 194 601