Электрический ток (работа 1)

Переменный электрический ток и его применение в медицине.

    Переменный ток, его виды и основные характеристики.

Переменный ток – это такой ток, направление и числовое значение которого меняются с течением времени (знакопеременный ток).

Примечание: не оговаривается форма кривой тока, периодичность, длительность его изменения.

На практике под переменным током чаще всего подразумевают периодический переменный ток.

Физическая сущность переменного тока сводиться к колебаниям электрических зарядов в среде (проводнике или диэлектрике).

Виды тока:

    Ток проводимости.

    Ток смещения.

Ток проводимости – это такой ток, который обусловлен колебаниями электронов и ионов в среде.

Ток смещения – это ток, который обусловлен смещением электрических зарядов на границе «проводник – диэлектрик» (например, ток через конденсатор).

Ток смещения связан с изменением во времени электрического поля на границе проводник – диэлектрик и имеет особенности:

    Амплитуда тока смещения и его направления совпадают по фазе с таковыми тока проводимости.

    По значению он всегда равен току проводимости.

Частным случаем тока смещения является ток поляризации. Ток поляризации – это ток смещению не в вакууме, а в материальной диэлектрической среде.

Сумма токов смещения и поляризации составляет полный ток смещения.

В медицинской практике применяются следующие виды токов по форме кривой тока:

    Синусоидальный

    Прямоугольный

    Треугольный

    Трапециевидный

    Игольчато-экспоненциальный

Самым простым является периодический синусоидальный ток. Он легко описывается математически и графически, форма его не искажается в электрических цепях с R, C, L элементами.

Основные характеристики переменного тока.

    Период – время одного цикла изменения тока по направлению и числовому значению (T, c).

    Частота – это число циклов изменения тока в единицу времени.

 =1/Т (величина обратная периоду с-1, Гц)

    Круговая частота (, 2/Т радиан/с)

    Фаза () – это величина, определяющая во времени взаимоотношение тока и напряжения в электрической цепи.

    Мгновенное значение тока и напряжения - значение этих величин в данный момент времени (i, u).

    Амплитудное значение тока и напряжения – это максимальное за полупериод значение этих величин (I>m>>, >U>m>).

    Среднеквадратическое (действующее, эффективное) значение тока и напряжения - вычисляется как положительный квадратный корень из среднего значению квадрата напряжения или тока по формулам.

I = I2>cp>

U = U2>cp>

Среднее значение (U>ср>) за период (постоянная составляющая) – это среднее арифметическое мгновенных значений ток или напряжения за период.

На практике среднеквадратическое значение определяется по эффективному (действующему) значению. (I>cp>>,>U>cp>), которое для синусоидального тока вычисляется по формулам:

I>эф> = I = 0,707 I>m>

U>эф> = U = 0,707 U>m>

В отдельных случаях медицинского применения электрического тока приходиться учитывать и другие характеристики (например, коэффициент амплитуды К>а>, и коэффициент формы К>ф>).

Для практики имеют значения следующие формулы связи характеристик:

i(u) ≤I>m>(U>m>)

I>эф> = I = I>m>/2> >=0,707 I>m >I>m = >1,41 I>эф>

U>эф> = U= U>m>/2> >=0,707 U>m >U>m = >1,41 U>эф>

2. Цепи переменного тока с активным сопротивлением, индуктивностью, емкостью и их особенности.

Электрическая цепь - это реальная или мыслимая совокупность физических элементов, передающих электрическую энергию от одной точки пространства к другой.

Физическими элементами электрических цепей являются проводники, резисторы, конденсаторы, катушки индуктивности. Элементы цепи являются и элементами её связи, и, кроме того, реализуют соответствующие свойства сопротивления, емкости и индуктивности.

Виды электрических цепей:

    Простые.

    Сложные.

Простые цепи содержат только единичные R, C, L – элементы, а сложные имеют их в различных количествах и сочетаниях.

Общей особенностью элементов электрической цепи является то, что при прохождении переменного тока они оказывают сопротивление, которое называется активным (R), индуктивным (X>l>), емкостным (X>c>).

Особенности простых идеальных цепей.

Цепь, состоящая из генератора тока и идеального резистора, называется простой цепью с активным сопротивлением.

Условию идеальности цепи:

    Активное сопротивление не равно нулю,

    индуктивность и ёмкость его равны нулю.

R  0

L>r> = 0

C>r> = 0 ~ R

Особенности:

    Соблюдается закон Ома для мгновенных, амплитудных и среднеквадратичных значений тока и напряжения.

    Активное сопротивление не зависит от частоты (поверхностный «скин - эффект» не учитываем)

    Нет сдвига фаз () между током и напряжением.

Это значит, что ток и напряжение одновременно проходят свои максимальные (амплитудные) и нулевые значения.

    На R – элементе происходят потери энергии в виде выделения тепла.

Цепь с индуктивностью – это электрическая цепь, состоящая из генератора переменного тока и идеального L – элемента- катушки индуктивности.

Условия идеальности цепи:

    Индуктивность катушки не равна нулю

    Её ёмкость и сопротивление равны нулю.

L  0

R>L>= 0

C>L> = 0

Особенности цепи:

    Соблюдается закон Ома.

    L- элемент оказывает переменному току сопротивление, которое называется индуктивным. Оно обозначается X>L>> > и возрастает с увеличением частоты линейно, соответственно формуле:

X>L>> >= L = 2L

    В цепи есть сдвиг фаз между напряжением и током: V опережает I по фазе на угол /2

    Индуктивное сопротивление не потребляет энергии, т.к. она запасается в магнитном поле катушки, а затем отдается в электрическую цепь. Поэтому индуктивное сопротивление называется кажущимся или мнимым.

Цепь с ёмкостью – это электрическая цепь, состоящая из генератора переменного тока и идеального C – элемента - конденсатора.

Условия идеальности цепи:

    Ёмкость конденсатора не равна нулю, а его активное сопротивление и индуктивность равны нулю. С  0, R>С>= 0, L>C> = 0.

Особенности цепи с ёмкостью:

1. Соблюдается закон Ома.

2. Ёмкость оказывает переменному току сопротивление, которое называется ёмкостным. Оно обозначается X>с > и уменьшается с увеличением частоты не линейно.

    В цепи есть сдвиг фаз между напряжением и током: V отстает от I по фазе на угол /2

    Ёмкостное сопротивление не потребляет энергии, т.к. она запасается в электрическом поле конденсатора, а затем отдается в электрическую цепь. Поэтому ёмкостное сопротивление называется кажущимся или мнимым.

    Полная цепь переменного тока и её виды. Импеданс и его формула. Особенности импеданса живой ткани.

Полная цепь переменного тока - это цепь из генератора, а также R, C, и L элементов, взятых в разных сочетаниях и количествах.

Для разбора проходящих в электрических цепях процессов используют полные последовательные и параллельные цепи.

Последовательная цепь - это такая цепь, где все элементы могут быть соединены последовательно, один за другим.

В параллельной цепи R, C, L элементы соединены параллельно.

Особенности полной цепи:

    Соблюдается закон Ома

    Полная цепь оказывает переменному току сопротивление. Это сопротивление называется полным (мнимым, кажущимся) или импедансом.

    Импеданс зависит от сопротивления всех элементов цепи, обозначается Z и вычисляется не простым, а геометрическим (векторным) суммированием. Для последовательно соединенных элементов формула импеданса имеет следующее значение:

здесь:

Z - импеданс последовательной цепи,

R - активное сопротивление,

X>L>> >– индуктивное и X>C> – ёмкостное сопротивление,

L - индуктивность катушки (генри),

C - ёмкость конденсатора (фарад).

Так как ёмкостное и индуктивное сопротивления дают для напряжения сдвиг фаз в противоположном направлении, возможен случай, когда X>L> = X>C>. При этом алгебраическая сумма модулей будет равна нулю, а импеданс – наименьшим.

Состояние, при котором в цепи переменного тока ёмкостное сопротивление равно индуктивному, называется резонансом напряжения. Частота, при которой X>L> = X>C>, называется резонансной частотой. Эту частоту >p> можно определить по формуле Томсона:

    Особенности импеданса живой ткани и её эквивалентная электрическая схема.

При пропускании тока через живую ткань, её можно рассматривать как электрическую цепь, состоящую из определенных элементов.

Экспериментально установлено, что это цепь обладает свойствами активного сопротивления и ёмкости. Это доказывается выделением тепла и уменьшением полного сопротивления ткани с возрастанием частоты. Свойств индуктивности у живой ткани практически не обнаруживается. Таким образом, живая ткань представляет собой сложную, но не полную электрическую цепь.

Импеданс живой ткани можно рассматривать как для последовательного, так и для параллельного соединения её элементов.

При последовательном соединении токи через элементы равны, общее приложенное напряжение будет векторной суммой напряжений на R и C элементах и формула импеданса последовательной цепи будет иметь вид:

Z_ - импеданс последовательной цепи,

R - её активное сопротивление,

X>C> - ёмкостное сопротивление.

При параллельном соединении напряжения на R и C элементах равны, общий ток будет векторной суммой токов каждого элемента, а фомула импеданса будет следующей:

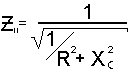
Теоретические формулы импеданса живой ткани при параллельном и последовательном соединении её элементов от экспериментальных отличаются следующим:

    При последовательной схеме соединения практические данные дают большие отклонения на низких частотах.

    При параллельной схеме эти измерения показывают конечное значение Z, хотя теоретически оно должно стремиться к нулю.

Эквивалентная электрическая схема живой ткани – это условная модель, приближенно характеризующая живую ткань, как проводник переменного тока.

Схема позволяет судить:

    Какими электрическими элементами обладает ткань

    Как соединены эти элементы.

    Как будут меняться свойства ткани при изменении частоты тока.

В основе схемы лежат три положения:

    Внеклеточная среда и содержимое клетки есть ионные проводники с активным сопротивлением среды Rср и клетки Rк.

    Клеточная мембрана есть диэлектрик, но не идеальный, а с небольшой ионной проводимостью, а, следовательно, и сопротивлением мембраны Rм.

    Внеклеточная среда и содержимое клетки, разделённые мембраной, являются конденсаторами См определенной ёмкости (0,1 – 3,0 мкФ/см2).

Если в качестве модели живой ткани взять жидкую тканевую среду – кровь, содержащую только эритроциты, то при составлении эквивалентной схемы нужно учитывать пути электрического тока.

Их два:

    В обход клетки, через внеклеточную среду.

    Через клетку.

Путь в обход клетки представлен только сопротивлением средыRср.

Путь через клетку сопротивлением содержимого клетки Rк, а также сопротивлением и ёмкостью мембраны.Rм, См.

Если заменить электрические характеристики соответствующими обозначениями, то получим эквивалентные схемы разной степени точности:

Схема Фрике (ионная проводимость не

учитывается).

Схема Швана (ионная проводимость учитывается в виде сопротивления мембраны)

Обозначения на схеме:

Rcp - активное сопротивление клеточной среды

Rk - Сопротивление клеточного содержимого

Cm - ёмкость мембраны

Rm - сопротивление мембраны.

Анализ схемы показывает, что при увеличении частоты тока проводимость клеточных мембран увеличивается, а полное сопротивление тканевой среды уменьшается, что соответствует практически проведенным измерениям.

5. Живая ткань как проводник переменного электрического тока. Дисперсия электропроводности и её количественная оценка.

Экспериментально установлены следующие особенности живой ткани как проводника переменного ток:

1. Сопротивление живой ткани переменном току меньше, чем постоянному.

2. Электрические характеристики ткани зависят как от её вида, так и от частоты тока.

3. С увеличением частоты полное сопротивление живой ткани нелинейно уменьшается до определенного значения, а затем остаётся практически постоянным (в большинстве на частотах свыше 106 Гц)

4. На определенной частоте полное сопротивление зависит также от физиологического состояния (кровенаполнения), что используется на практике. Исследование периферического кровообращения на основе измерения электрического сопротивления называются реография (импедансплетизмография).

5. При умирании живой ткани её сопротивление уменьшается и от частоты не зависит.

6. При прохождении переменного тока через живые ткани наблюдается явление, которое называется дисперсией электропроводности.

Д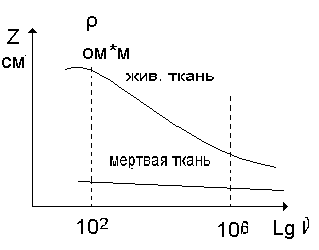исперсия электропроводности - это явление зависимости полного (удельного) сопротивления живой ткани от частоты переменного тока.

Графики такой зависимости называют дисперсионными кривыми. Дисперсионные кривые строят в прямоугольной системе координат, где по вертикали откладывают значения полного (Z) или удельного сопротивления, а по горизонтали - частоту в логарифмическом масштабе (Lg ).

Частотные зависимости по форме кривой для разных тканей сходный, но отличается значением сопротивления.

Имеется несколько диапазонов частот, на которых дисперсия особенно выражена. Один из них соответствует интервалу 102 -106 Гц

Особенности дисперсии:

1. Присуща только живым тканям.

2. Более выражена на частотах до 1 МГц.

3. На практике используется для оценки физиологического состояния и жизнеспособности тканей.

Количественно оценка дисперсии проводиться по коэффициенту дисперсии (К).

Коэффициент дисперсии это безразмерная величина, равная отношению низкочастотного (102) полного (или удельного) сопротивления к высокочастотному (106 Гц).

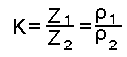
Z>1 >– полное сопротивление на частоте 102> >Гц

Z>2 >– полное сопротивление на частоте 106 Гц

>1>, >2 >- удельное сопротивление на этих частотах

Значение коэффициента дисперсии зависит от вида ткани, её физиологического состояния, эволюционной стадии развития животного. Например, для печени животного К = 9 -10 единиц, а для печени лягушки 2 -3 единицы. При умирании ткани коэффициент дисперсии стремиться к единице.

Явление дисперсии связывают с наличием в живых тканях поляризации, которая с увеличением частоты меньше влияет на полное сопротивление. Поэтому коэффициент дисперсии часто называют коэффициентом поляризации.

Кроме частотных зависимостей в живых тканях отмечаются фазовые сдвиги между током и напряжением, которые тоже, но в меньшей степени, зависят от частоты.

Фазовые сдвиги тоже уменьшаются при умирании тканей и, в перспективе, могут быть использованы для практических целей.