Течения жидких и газообразных сред
Течения жидких и газообразных сред бывают двух типов:
1) спокойные, плавные и 2) нерегулярные, со значительным перемешиванием объемов среды и хаотическим изменением скоростей и других параметров. Первые называют ламинарными, а для вторых английский физик У. Томсон предложил термин "турбулентные" (от англ. turbulent - бурный, беспорядочный).
Большинство течений в природе и технике относятся именно ко второй, наименее изученной группе. В этом случае применяют статистические (связанные с осреднением по времени и пространству) способы описания. Во-первых, потому, что практически невозможно уследить за пульсациями в каждой точке течения, а во-вторых, эти данные бесполезны: их нельзя использовать в конкретных приложениях.
Поскольку турбулентность - одно из глубочайших явлений природы, при самом общем подходе к его изучению оно смыкается с философским проникновением в суть вещей. Знаменитый ученый Т. Карман очень образно охарактеризовал это, сказав, что, когда предстанет перед Создателем, первое откровение, о котором будет просить, - раскрыть тайны турбулентности.
Наибольший практический интерес представляют такие течения, которые соответствуют весьма большим числам Рейнольдса Re = u>0>b/. В эту безразмерную величину входят основная скорость u>0> (в струе - скорость истечения, для самолета - скорость полета), характерный линейный размер b (диаметр сопла или хорда крыла) и вязкость среды . Число Рейнольдса определяет соотношение инерционных сил и сил трения (вязкости). Типичные значения этого числа в авиации таковы: Re=105-107.
Что такое вихревая аэродинамика?
Вихревые течения воды и воздуха известны нам с детства. Ставя запруды в ручьях, мы могли наблюдать, как, обтекая края, вода интенсивно вращается, образуя водовороты. Когда вода вытекает из ванны, появляется жидкая воронка с вращением. За летящим самолетом можно отчетливо видеть два устойчивых следа: это с концов крыла сходят вихревые жгуты, которые тянутся на много километров. Вихревые течения представляют собою вращающиеся объемы среды - воды, воздуха и т.д. Если сюда поместить маленькую крыльчатку, она также станет вращаться.
Простейший математический образ, описывающий чисто вращательное движение жидкости, - тонкая прямолинейная нить бесконечной длины. Из соображений симметрии ясно, что во всех плоскостях, перпендикулярных нити, картина скоростей одинакова (плоскопараллельное течение). Кроме того, на любой окружности радиуса r с центром на нити скорость v будет направлена по касательной к окружности и постоянна по величине.
Интенсивность вихря принято характеризовать циркуляцией скорости по замкнутому контуру, охватывающему вихрь. В данном случае на окружности радиуса r циркуляция =2rv. В силу теоремы о постоянстве циркуляции, справедливой для идеальной (лишенной трения) среды, не зависит от r. В результате получаем частный вид формулы Био-Савара
v=/2r (1)
Как видно из уравнения (1), по мере приближения к оси вихря (т. е. при r 0) скорость неограниченно возрастает (v ) как 1/r. Такую особенность принято называть сингулярной.
17 января 1997 г. исполнилось 150 лет со дня рождения Н. Е. Жуковского, "отца русской авиации". Он заложил теоретическую базу современной аэродинамики, сделав ее основой авиации: установил механизм образования подъемной силы крыла в идеальной жидкости, ввел понятие присоединенных (неподвижных относительно крыла) вихрей, стал родоначальником так называемого вихревого метода. Согласно этому методу, крыло или летательный аппарат (ЛА) заменяют системой присоединенных вихрей, которые в силу теоремы о сохранении циркуляции порождают свободные (не несущие) вихри, движущиеся вместе с жидкой средой. При этом задача сводится к определению интенсивности всех вихрей и положения свободных вихрей. Вихревой метод оказался особенно эффективным с появлением компьютеров и созданием численного метода дискретных вихрей (МДВ) [2, 4-7, 11-13].
Вихревая компьютерная концепция турбулентных следов и струй
За последние десятилетия достигнут значительный прогресс в изучении фундаментальных проблем турбулентности, чем мы обязаны прежде всего А. Н. Колмогорову и А. М. Обухову, их ученикам и последователям, а также их предшественникам Л. Ричардсону и Д. Тейлору [1].
При больших числах Re общепринятым стало понимание турбулентности как иерархии вихрей разных размеров, когда имеют место пульсации скорости потока от больших до самых малых значений. Крупномасштабная турбулентность определяется формой обтекаемого тела или конфигурацией сопла, откуда вытекает струя, режимом истечения, состоянием внешней среды. Здесь силы вязкости при формировании следов и струй можно не учитывать. При описании мелкомасштабных турбулентных течений на определенном этапе следует вводить в рассмотрение механизм молекулярной вязкости.
Согласно теории Колмогорова-Обухова, локальное строение мелкомасштабной развитой турбулентности в значительной степени описывается универсальными закономерностями. Доказано, что в области достаточно малых масштабов должен господствовать статистический универсальный режим, практически стационарный и однородный.
Обосновано также существование некоторого промежуточного режима турбулентности - инерционного, возникающего на масштабах, малых по сравнению с характерным размером течения в целом, но больших, чем тот микромасштаб, где уже существенны явления вязкости. Таким образом, в этом интервале, как и в начальной стадии турбулентности, вязкость среды можно не учитывать.
Однако общая теория турбулентности, которая содержала бы не только качественное описание основных процессов, но и количественные соотношения, позволяющие определять турбулентные характеристики, еще не создана. Построение строгой в математическом смысле теории затруднено еще и тем, что едва ли возможно дать исчерпывающее определение самой турбулентности.
С другой стороны, на вопросы, возникающие в связи с разнообразными техническими приложениями, требовались оперативные ответы - хотя бы и приближенные, но научно обоснованные. В результате стала интенсивно развиваться так называемая полуэмпирическая теория турбулентности, в которой наряду с теоретическими закономерностями и расчетами используются экспериментальные данные. Вклад в становление этого направления внесли такие ученые, как Д. Тейлор, Л. Прандль и Т. Карман [1]. Развитию и внедрению в практику этих подходов содействовали Г. Н. Абрамович [10], А. С. Гиневский [3] и др.
В полуэмпирической теории турбулентности проблема рассматривается упрощенно, поскольку изучаются не все статистические характеристики, а только самые важные для практики - в первую очередь средние скорости и средние значения квадратов и произведений пульсационных скоростей (так называемые моменты 1-го и 2-го порядков). Недостаток такого подхода прежде всего в том, что надо из эксперимента получать целый ряд данных для каждой группы конкретных условий: для тел разных форм при изучении следов, для различных конфигураций сопл, из которых истекают струи, и т. д. Кроме того, эта теория основана на стационарных подходах (развитие процесса во времени не рассматривается), что сужает ее возможности.
Развиваемая в данное время вихревая компьютерная концепция турбулентных следов и струй представляет собой замкнутую конструктивную математическую модель (ММ). Она основана на использовании всех достижений вихревой аэродинамики, завоеванных применением МДВ, для реализации тех современных представлений о турбулентности, о которых шла речь выше [1, 13]. Построение ММ ведется для больших чисел Re и базируется на трактовке свободной турбулентности как иерархии вихрей разного масштаба. При этом турбулентное движение рассматривается в общем случае как трехмерное и нестационарное.
Практическая реализация моделирования нестационарных струйных течений осуществляется методом дискретных вихрей. При этом непрерывная по пространству и времени модель заменяется ее дискретным аналогом. Дискретизация по времени состоит в том, что процесс полагается изменяющимся скачкообразно в моменты времени t>n>=nt (n=1,2,...). Дискретизация по пространству заключается в замене непрерывных вихревых слоев гидродинамически замкнутыми системами вихревых элементов (вихревых нитей или рамок). Важен также учет в ММ того обстоятельства, что свободные вихри движутся со скоростями жидких частиц, причем число их со временем возрастает.
Указанный подход к моделированию течений позволяет без привлечения дополнительной эмпирической информации исследовать общий характер развития процесса во времени. ММ, созданные на базе МДВ, описывают все главные черты развития турбулентных следов, струй и отрывных течений, включая переход от детерминированных процессов к хаосу. Они позволяют также рассчитывать статистические характеристики турбулентности (моменты 1-го и 2-го порядков).
Главное внимание здесь уделено компьютерному расчету обтекания тел, построению ближних участков следов и струй. Большой материал, накопленный учёными в этой области, включает не только прямые сопоставления расчета с экспериментом, но и проверку ММ на выполнение универсальных законов Колмогорова-Обухова развитой турбулентности, которые, таким образом, играют роль независимых тестов [2, 9, 11-14]. Численный эксперимент в сочетании с физическим и комплексный анализ результатов привели к следующим выводам [8].
Основные черты и макроэффекты отрывного обтекания тел при больших числах Re, в том числе ближний след и его характеристики, при известных местах отрыва потока (на острых кромках, изломах, срезах тел и т. д.), а также в струях не зависят от вязкости среды; они определяются инерционным взаимодействием в жидкостях и газах, которые описывают нестационарные уравнения идеальной cреды.
Дальнейший анализ показал, что в ряде задач необходимо учитывать и вязкие отрывы, особенно на поверхности гладких тел (таких, как круговые и эллиптические цилиндры). Поэтому следующий шаг в развитии данной концепции состоял в том, что нестационарные модели идеальной среды были дополнены нестационарными уравнениями пограничного слоя для определения места отрыва [6].
Таким образом, была обоснована и осуществлена смена приоритетов: на первый план вышла не вязкость среды, а нестационарные явления.
Основополагающая работа Жуковского "О присоединенных вихрях" была опубликована в 1906 г. Современность выдвинула новые проблемы, а компьютерные технологии расширили области применимости теоретических методов. Классические идеи Жуковского переживают ныне вторую молодость, открывая новые возможности теории идеальной среды и вихревых методов.
Важно подчеркнуть, что в природе вихревые течения и хаос живут бок о бок, становясь прародителями турбулентности. Вращение жидких объемов порождает неустойчивость, а также появление и распад регулярных структур, что ведет к образованию новых вихрей и развитию хаоса.
Некоторые результаты
На рис. 1 и 2 приведены примеры когерентных вихревых структур, полученных расчетным путем на компьютерах. Такое название получили крупномасштабные, в той или иной степени упорядоченные вихревые структуры, образующиеся в вихревых следах и струях. В последние годы им стали уделять большое внимание, установив, что они играют существенную роль в явлениях турбулентности [1, 10, 11, 13].

Рис.1
Рис.2
Одной из классических задач является задача об отрывном обтекании пластины, поставленной перпендикулярно набегающему потоку. Если угодно, это модель обтекания запруды, установленной поперек ручья. Еще в начале столетия Карман, постулируя наличие вихревой дорожки с шахматным расположением точечных дискретных вихрей, нашел соотношение между шириной дорожки h и продольным расстоянием между вихрями l:
h/l=0.28. (2)
Однако в 30-х годах в работах Н. Е. Кочина, В. В. Голубева и др. было показано, что вывод этого уравнения по теории возмущений (в предположении устойчивости дорожки) некорректен. Оказалось, что устойчивость сохраняется только при частном виде возмущений. С другой стороны, эксперименты подтверждали соотношение (2).
Только в 70-х годах удалось разгадать этот парадокс [2]. Допуская сход свободных вихрей с кромок пластин (иначе скорости обращаются здесь в бесконечность) и решая нестационарную отрывную задачу с помощью МДВ, мы пришли к картине, изображенной на рис. 1. При этом объемные вихревые сгустки хотя и деформируются, но расстояния между их центрами соответствуют формуле (2). На рис. 2 изображены мгновенные картины крупномасштабных вихревых образований в плоской турбулентной струе, истекающей с начальной скоростью u>0> из канала ширины 2r. Безразмерное время введено по формуле =u>0>t/r. Каждая из замкнутых кривых соответствует сгустку завихренностей одного знака (или с явным преобладанием вихрей одного направления вращения). С помощью МДВ процесс моделировался от начала истечения (=0). Границы струи заменялись дискретными вихрями, которые теряли устойчивость и, наряду со средней регулярной скоростью, приобретали флуктуации.

Рис.3
Одной из ответственных проверок построенной ММ стала задача об истечении струи из круглого сопла. Оказалось, что осесимметричная схема недостаточна (турбулентные течения не терпят искусственных ограничений). Зато пространственная нестационарная ММ привела к полному успеху. Рис. 3 показывает, как трансформируется вихревая граница струи. Начальный участок сохраняет осевую симметрию; затем она разрушается, но просматривается тенденция к формированию когерентных структур.
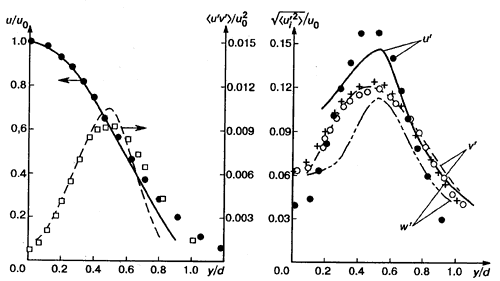
Рис.4
На
рис. 4 сопоставляются результаты расчета
и эксперимента в сечении x/d=4 для средних
пульсаций скоростей истечения
 /u>0>
(здесь u>1>'=u',u>2>'=v',u>3>'=w')
и рейнольдсовых напряжений сдвига
u'v'/u>0>2.
/u>0>
(здесь u>1>'=u',u>2>'=v',u>3>'=w')
и рейнольдсовых напряжений сдвига
u'v'/u>0>2.
Вихревая безопасность полетов
Результатом многолетних исследований стало развитие вихревой компьютерной концепции турбулентности. Впервые была создана и многократно опробована замкнутая ММ турбулентных следов и струй, в которой не требуется прибегать к экспериментальным данным. На повестке дня - систематическое использование созданного аппарата в поисковых и прикладных исследованиях.
Остановимся подробнее на одной области приложений, которая уже приобретает реальную жизнь, - на проблеме вихревой безопасности полетов. Образование аэродинамической подъемной силы всегда сопровождается возникновением и сходом в поток свободных вихрей. Они превращаются в устойчивые вихревые жгуты, которые тянутся за тяжелыми самолетами 10-15 км (рис. 5). По сути дела, это еще один тип когерентных вихревых структур, очень мощных и опасных: попадание в них других ЛА чревато аварией или даже катастрофой.

Рис.5
Впервые с этой проблемой столкнлись в 1968 г., в комиссии по расследованию обстоятельств гибели Юрия Гагарина [15]. Он совершал тренировочный полет на самолете-спарке УТИ Миг-15 вместе с инструктором Серегиным, опытным боевым летчиком. Было доказано, что самолет вышел на закритический режим и попал в "штопор" (неуправляемое вращение). Учитывая надежность самолета, главное внимание и горячие дискуссии вызвал вопрос, что могло стать причиной этого. В конце концов всесторонний анализ с привлечением методов моделирования на ЭВМ привел нас к заключению: причиной было неожиданное сближение с другим самолетом и резкий маневр на уклонение с возможным попаданием в вихревой след впереди летящего самолета.
На рис. 5 изображено положение двух жгутов, в которые собираются свободные вихри самолета. Вначале, при полете на значительной высоте, они движутся параллельно и из-за взаимодействия с соседними вихрями опускаются. У земли, поверхность которой препятствует дальнейшему снижению, начинается разбегание жгутов в стороны. Причину этого легко понять: на поверхности земли не может быть вертикальных скоростей. Это "условие непротекания" можно обеспечить введением фиктивных зеркально отраженных вихрей, которые, кроме того, создают боковые скорости, ведущие к разбеганию жгутов.
Сказанное объясняет причины другой катастрофы, которая произошла в Ташкенте в 1987 г. при поочередном взлете самолетов Ил-76, и Як-40. Все требования инструкции были выполнены, но второй самолет попал в след первого, начал резко крениться и врезался в землю: эффективности элеронов не хватило. Анализ ситуации и моделирование дали следующий результат. На аэродроме при хорошей погоде дул небольшой ветер 0.5-1.0 м/с. Из-за этого один из вихревых жгутов завис над взлетной полосой, и Як-40 на расстоянии 6-7 км попал в него. Такая небольшая величина бокового ветра оказалась критической. В дальнейшем это обстоятельство было отражено в инструкции.
Вихревые жгуты - компактные вихревые структуры, образующие длинный след за самолетом.
Вихревые течения - вращающиеся объемы жидкой среды.
Когерентные вихревые структуры - крупномасштабные квазиустойчивые вихревые образования.
ЛА - летательный аппарат.
МДВ - численный метод дискретных вихрей.
ММ - математическая модель.
Моменты второго порядка - осредненные по времени произведения и квадраты пульсаций скоростей: u'2, v'2, w'2 и т.д.
Пульсации скоростей среды (u',v',w') - добавки к средним значениям скоростей среды, меняющиеся во времени.
Турбулентность - нерегулярные течения среды с сильным перемешиванием и хаотическим изменением параметров.
ЛИТЕРАТУРА
1. Монин А. С., Яглом А. М. Статистическая гидромеханика. Т. 1. СПб: Гидрометеоиздат, 1992.
2. Белоцерковский С. М., Ништ М. И. Отрывное и безотрывное обтекание крыльев идеальной жидкостью. М.: Наука, 1978.
3. Гиневский А. С. Теория турбулентных струй и следов. М.: Машиностроение, 1969.
4. Belotserkovsky S. M. The theory of thin wings in sub>sonic flow. N. Y.: Plenum Press, 1967.
5. Belotserkovsky S. M., Lifanov I. K. Method of discrete vortices. Boca Raton: CRC Press, 1994.
6. Belotserkovsky S. M., Kotovskii V. N., Nisht M. I., Fedorov R. M. Two-dimensional separated flows. Boca Raton: CRC Press, 1994.
7. Belotserkovsky S. M. Study of the unsteady aerodynamics of lifting surface using the computer // Ann. Rev. Fluid Mech. 1977. V. 9. P. 469-494.
8. Белоцерковский О. М., Белоцерковский С. М., Давыдов Ю. М., Ништ М. И. Отрывное обтекание тел с фиксированными местами отрыва // ДАН СССР. 1983. Т. 273, № 4. С. 821-825.
9. Белоцерковский С. М. О моделировании на ЭВМ турбулентных струй и следов методом дискретных вихрей // Этюды по турбулентности. М.: Наука, 1994. С. 246-248.
10. Абрамович Г. Н., Гиршович Т. А., Крашенников С. Ю., Секундов А. Н., Смирнова И. П. Теория турбулентных струй. М.: Наука, 1984.
11. Белоцерковский С.М., Гиневский А.С. Компьютерная концепция вихревой турбулентности // Изв. вузов. Нелинейная механика. 1995. Т. 3, № 2. С. 72-93.
12. Белоцерковский С. М., Хлапов Н. В. Моделирование влияния диффузии вихрей на турбулентные характеристики струй /Там же. С. 94- 103.
13. Белоцерковский С. М., Гиневский А. С. Моделирование турбулентности струй и следов на основе метода дискретных вихрей. М.: Наука, 1995.
14. Белоцерковский С. М., Гиневский А. С., Хлапов Н. В. Моделирование круглой турбулентной струи методом дискретных вихрей // ДАН. 1995. Т. 345, № 4. С. 479-482.
15. Белоцерковский С. М. Гибель Гагарина. М.: Машиностроение, 1992.