Связанные контура
связанные контура
Содержание
Введение. 2
Основные понятия. 2
Контур, эквивалентный связанным контурам. Вносимые сопротивления. 3
Резонансные характеристики системы двух связанных контуров. 6
Полоса пропускания системы двух связанных контуров. 13
Энергетические соотношения в связанных контурах. 13
Настройка системы двух связанных контуров. 14
Прохождение радиоимпульса через двухконтурную связанную систему 17
литература 20
Введение.
В радиотехнике широкое применение находят всевозможные колебательные контура. Основное назначение радиотехнических колебательных цепей - получение с их помощью частотной избирательности, т.е. выделения полезного сигнала и подавления всех остальных сигналов и помех. Ввиду того что с помощью одиночного колебательного контура нельзя получить высокую избирательность при широкой полосе пропускания, используют связанные контуры. В радиотехнике такие контуры применяются в основном как фильтры промежуточной частоты (ФПЧ).
Основные понятия.
Два контура называются связанными, если колебания, происходящие в одном из них, захватывают другой контур. Связь между контурами может осуществляться через электрическое поле (благодаря емкости) или через магнитное поле (благодаря взаимоиндуктивности или индуктивности). На рис. 1 показаны три разновидности связи двух колебательных контуров: а) трансформаторная, когда связь между контурами осуществляется благодаря взаимоиндуктивности между катушками L1 и L2; б) автотрансформаторная, когда связь между контурами осуществляется непосредственно через индуктивность связи L1,2; в) емкостная, когда связь между контурами осуществляется через емкость связи С3. Наиболее часто в радиотехнике применяется трансформаторная связь, поэтому все дальнейшие выкладки проведем для этого вида связи.

Рис. 1. Виды связи двух колебательных контуров
Предположим, что в первом контуре на рис.1, а протекает ток i>1>, а второй контур разомкнут. Тогда отношение напряжения, индуцированного в катушке L2, к напряжению в катушке L1 выразится коэффициентом

который называется степенью связи. Аналогично, если предположить разомкнутым первый контур, а источник э.д.с. подключить ко второму контуру, то при протекании в нем тока i>2> получим

Коэффициент
связи
есть корень квадратный из произведения
степеней связи
 .
(1)
.
(1)
При
трансформаторной связи
 .
(2)
.
(2)
Если умножить числитель и знаменатель (2) на w, то получим общее выражение для коэффициента связи, пригодное и для других видов связи
 (3)
(3)
где X>M> - сопротивление связи.
Контур, эквивалентный связанным контурам. Вносимые сопротивления.
Рассмотрим систему двух колебательных контуров с трансформаторной связью, в которой к первому контуру подключен источник э.д.с. e(t) (рис. 2,а), а r>1> и r>2> - выделенные для анализа сопротивления потерь в контурах.

а

б
Рис.2. Система двух колебательных контуров с трансформаторной связью (а) и ее эквивалентная схема (б)
Запишем для каждого контура уравнения Кирхгофа
 (4)
(4)
Считая
э.д.с. синусоидальной и режим в цепи
установившимся, можно воспользоваться
символическим методом анализа. Тогда
 ;
;
 и (4) принимает вид
и (4) принимает вид
 (5)
(5)
Обозначив реактивное сопротивление первого и второго контуров через X>1> и X>2>, (5) можно записать так:
 (6)
(6)
Найдем
 из второго уравнения
из второго уравнения
 (7)
(7)
Обозначив wМ = X>СВ> (сопротивление связи), (7) можно переписать так:

Подставив
значение
 из (7) в первое уравнение системы (6)
из (7) в первое уравнение системы (6)

Освободившись от мнимости в знаменателе, получим

или

так как
 .
.
Поделив в
полученном выражении приложенную э.д.с.
на ток
 запишем выражение для эквивалентного
входного сопротивления системы двух
связанных колебательных контуров
запишем выражение для эквивалентного
входного сопротивления системы двух
связанных колебательных контуров
 (8)
(8)
Модуль сопротивления Z>1Э> равен
 (9)
(9)
Анализ (8)
показывает, что в результате связи
первого контура со вторым в первый
контур как бы вносятся два сопротивления:
активное

и реактивное
 (10)
(10)
Таким образом, систему двух связанных колебательных контуров можно заменить одним эквивалентным контуром (рис. 2, б), в который вносится сопротивление

Суммарное активное сопротивление R>1э> = r>1>+ R>вн> всегда положительное, а знак суммарного реактивного сопротивления Х>1э>=Х>1>+Х>вн> определяется настройкой каждого из контуров в отдельности (знаки X>1> и Х>2 >и, следовательно, Х>вн> зависят от частоты, на которую настроен каждый контур).
Резонансные характеристики системы двух связанных контуров.
Под амплитудно-частотными резонансными характеристиками системы двух связанных контуров будем подразумевать зависимость амплитуд токов первого и второго контуров от частоты. Считая, что оба контура настроены на одну и ту же частоту w>0 >выделим модули тока первого и второго контуров при наличии связи между ними.
Если
записать в символической форме
 и
и
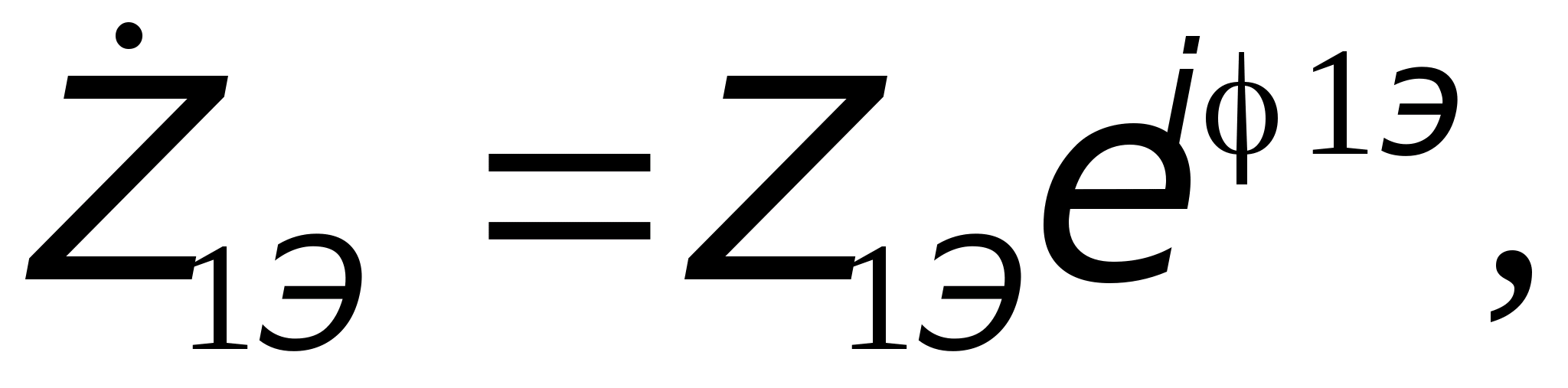 то
то
 (11)
(11)
где
 Модуль (11) есть
Модуль (11) есть
 (12)
(12)
На основании
(7), с учетом того что
 и
и
 имеем
имеем
 (13)
(13)
где
 и
и
 .
Запишем Модуль (13) с учетом (12) и (9)
.
Запишем Модуль (13) с учетом (12) и (9)

Выражения (12) и (14) представляют собой уравнения резонансных характеристик для I>1> и I>2> соответственно в неявной относительно частоты форме. Таким образом, если построить зависимости модулей I>1> и I>2 >от частоты, то это и будут амплитудно-частотные резонансные характеристики. При построении их будем исходить из двух случаев связи между контурами; слабой и сильной. Сначала займемся построением I>1>(). Как видно из (12), частотную зависимость I>1> определяет частотная зависимость Z>1э>(), поскольку э. д. с. источника Е от частоты не зависит. Таким образом, построение сводится сначала к построению зависимости Z>1э>(), а затем — зависимости I>1>() как частного от деления Е на Z>1э>.
Выразив модуль Z>1э>() через компоненты

построим попарно зависимости r>1> и r>вн> , Х>1> и Х>вн> от частоты, а Z>1э >найдем графически, как геометрическую сумму r>1>+ R>вн> и Х>1>+ Х>вн>. I>1> строим в соответствии с (12). Построение проводим при небольших расстройках относительно резонансной частоты. Получаемые зависимости при слабой связи между контурами имеют вид, показанный на рис. 3, а при сильной связи—на рис. 4.


Рис. 3. Частотные зависимости входного сопротивления, его составляющих и тока I>1> системы двух связанных контуров при слабой связи между ними
Рис. 4. Частотные зависимости входного сопротивления, его составляющих и тока I>1> системы двух связанных контуров при сильной связи между ними
Как видно, при слабой связи между контурами вследствие малости Х>ВН> по сравнению с Х>1 >кривая X>1э> () пересекает ось частот только в одной точке >о>. При сильной связи между контурами вследствие значительной величины Х>ВН>, которая на некоторых частотах превышает по абсолютной величине Х>1>, имея обратный знак, суммарная кривая Х>1э> () пересекает ось частот в трех точках: >01>> >, >0> и >02>. Другими словами, результирующее реактивное сопротивление системы равно нулю не только на частоте >0>, но и на частотах >01 >и >02>, называемых частотами связи. Учитывая еще то обстоятельство, что при сильной связи между контурами сопротивления R>ВН> на частоте >0 >и в близлежащей области большие, чем при слабой, понятен двугорбый характер кривых Z>1э>() и I>1>() с максимумами на частотах > 1> и > 2>.
Очевидно,
имеется граничная связь, превышение
которой ведет к двугорбости
амплитудно-частотной резонансной
характеристики тока первичного
контура. Такая связь называется первичной
критической связью,
а соответствующий ей коэффициент связи
— первичным
критическим коэффициентом связи
(k>кр1>).
Амплитудно-частотную резонансную
характеристику вторичного тока строим
на основании полученных характеристик
первичного тока и (14). Для того чтобы
можно было сравнивать амплитудно-частотные
резонансные характеристики первичного
и вторичного токов, их надо строить на
одном рисунке по отношению к
резонансным значениям Z>2>,
т.е.
 и.
и.
 .
Согласно (14)
.
Согласно (14)
 Таким образом , для построения
амплитудно-частотных характеристик
вторичного тока достаточно перемножить
координаты кривых I>1
>
(w)
/ I>1p
>
и r>2>
/Z>2
>(w)>
>
Таким образом , для построения
амплитудно-частотных характеристик
вторичного тока достаточно перемножить
координаты кривых I>1
>
(w)
/ I>1p
>
и r>2>
/Z>2
>(w)>
>
Указанные
построения для связи, меньше критической,
выполнены на рис. 5, а,
а для связи, больше критической,— на
рис. 2. 19, б.
Как
видно из рис. 5, б,
двугорбость кривой первичного тока
выражена резче, причем горбы разнесены
дальше, чем у кривой вторичного тока.
Очевидно, возможна такая связь между
контурами системы, когда двугорбость
первичного тока уже наступит, а вторичного
— еще нет. Такая связь, превышение
которой ведет к появлению двугорбости
у резонансной амплитудно-частотной
характеристики вторичного тока,
называется вторичной
критической связью,
а соответствующий ей коэффициент связи
-вторичным
критическим коэффициентом связи
(k>кр2>).
Рис. 5. Амплитудно-частотные характеристики вторичного тока системы двух связанных контуров при слабой (а) и сильной (б) связях между ними
Максимальные значения вторичного тока I>2> при связи, больше вторичной критической, наблюдаются на частотах связи >01> и >02>, при которых Х>1>=0. Для того чтобы найти условия возникновения частот связи и определить их значения, (11) и (13) нужно представить в явной относительно частоты форме и исследовать (13) на экстремум, т. е. установить, при каких относительных расстройках (e) вторичный ток будет максимальным и минимальным. Чтобы получить выражения для >1> и I>2> в явной относительно частоты форме, перепишем (11), подставив вместо Z>1э> его значение из (8)

Считая,
что контуры настроены в резонанс (>1>
= >2>=
>0>),
вынесем за скобки в знаменателе >0>L
и, подставив на основании (2)
 получим
получим

 (15)
(15)
где

 ,
,

 .
(16)
.
(16)
Модуль
тока
 равен
равен
 (17)
(17)
Подставив в (7) вместо М. его значение из (2) и домножив числитель и знаменатель (7) на w>0 >L>2 >,> > найдем,
 (18)
(18)
где
 .
Выражения (13) и (18) — идентичны.
Взяв модуль (18) и подставив значение
модуля I>1>
из (17), получим
.
Выражения (13) и (18) — идентичны.
Взяв модуль (18) и подставив значение
модуля I>1>
из (17), получим

 (19)
(19)
Если частота питающего генератора равна резонансной частоте контуров, т. е. >г> >0 >( = 0), то (19) упрощается

В относительных единицах выражение, описывающее резонансную кривую для тока I>2>, имеет вид
 (20)
(20)
Выражения (17) и (19) соответствуют (12) и (14) и описывают амплитудно-резонансные характеристики токов I>1> и I>2> в явной относительно частоты (расстройки e) форме.
Исследуем
(19) на экстремум, для чего продифференцируем
(19) по e
и приравняем производную нулю, т. е. dI
>2>
/de
= 0. В результате получим
 .
Данное уравнение имеет три корня:
.
Данное уравнение имеет три корня:

 (21)
(21)
При d>1 >= d>2> получаем
 (22)
(22)
Если первый
корень (e>1>)
действителен при любых соотношениях
между k
и d,
то второй и третий корни (>2>
и >3>)
имеют смысл только при k
> d.
При k<d
подкоренное выражение будет мнимым и
физического смысла не имеет. В этом
случае физический смысл имеет только
первый корень (>1>),
что говорит об одногорбости резонансной
характеристики для I>2>.
При k
> d
физический смысл имеют все три корня,
что говорит о двугорбом характере
резонансной характеристики для тока
I>2>.
Очевидно, вторичный критический
коэффициент связи, лежащий на границе
перехода от одногорбой кривой к
двугорбой, на основании (21) получается
тогда, когда корни (21) обращаются в нуль:
 При
d>1>
= d>2>
имеем:
При
d>1>
= d>2>
имеем:
k> кр2 >= d. (23)
Чтобы получить выражения для частот связи при k > k>кр2>, в (22) надо подставить значение = а/Q = 1 — >0>2/2. Тогда
 (24)
(24)
Именно на частотах w>01> и w>02> выполняется условие резонанса, благодаря чему ток /а достигает максимума (рис. 5, б).
Третья резонансная частота получается из условия >1> =0, или >1>=1->0>2/2=0; отсюда = >0>. При k > k>кр2> на частоте >0> резонансная характеристика тока I>2> имеет впадину. При k < k>кр2>, когда физический смысл имеет только первый корень , системе связанных контуров свойственна лишь одна резонансная частота >0> на которой наблюдается максимум тока I>2> (рис.5, а). Наличие одной резонансной частоты при k<k>кр> и появление частот связи при k>k>кр> хорошо иллюстрирует рис. 6.
Фазово-частотные
резонансные характеристики системы
двух связанных контуров представляют
собой частотную зависимость фазового
сдвига между токами
 и приложенной к системе э. д. с. Е.
Как следует из (11), сдвиг фазы между
током
и приложенной к системе э. д. с. Е.
Как следует из (11), сдвиг фазы между
током
 >
>и
э. д. с. Е
зависит от угла -j>1э>,
значение которого определяется (16).
Сдвиг фазы между током
>
>и
э. д. с. Е
зависит от угла -j>1э>,
значение которого определяется (16).
Сдвиг фазы между током
 и
э. д. с. Е
зависит от угла
и
э. д. с. Е
зависит от угла
 [см. (18) ]
и отличается от сдвига фазы между
током
[см. (18) ]
и отличается от сдвига фазы между
током
 и
э.д.с. Е
углом
и
э.д.с. Е
углом
 .
Фазово-частотные характеристики системы
двух связанных контуров изображены на
рис. 7.
.
Фазово-частотные характеристики системы
двух связанных контуров изображены на
рис. 7.
Полоса пропускания системы двух связанных контуров.
В одиночном
контуре относительная расстройка
= 2о
= 1/Q
= d.
Полоса пропускания системы может быть
как меньше полосы пропускания одиночного
контура (при k
<
k>кр>),
так и больше ее (при k³
k>кр>).
Самой широкой полосой пропускания
системы двух связанных контуров будет
такая, в пределах которой провал
амплитудно-частотной резонансной
характеристики системы лежит на уровне
1/ от максимального значения; при этом
e=2Dw/w>0>
»
3.1d а коэффициент связи, обеспечивающий
данную полосу, k=2.41d.
Как видно, при этом полоса пропускания
системы двух связанных контуров в три
раза шире полосы пропускания одиночного
колебательного контура. При критической
связи (k
= k>кр>=
d),
обеспечивающей
наибольшее приближение резонансной
характеристики в пределах полосы
пропускания к прямоугольнику, =
1,41d.
от максимального значения; при этом
e=2Dw/w>0>
»
3.1d а коэффициент связи, обеспечивающий
данную полосу, k=2.41d.
Как видно, при этом полоса пропускания
системы двух связанных контуров в три
раза шире полосы пропускания одиночного
колебательного контура. При критической
связи (k
= k>кр>=
d),
обеспечивающей
наибольшее приближение резонансной
характеристики в пределах полосы
пропускания к прямоугольнику, =
1,41d.

Рис.6. Зависимость резонансной частоты системы двух колебательных контуров от коэффициента связи

Рис.7. Фазово-частотные характеристики системы двух связанных контуров при различных коэффициентах связи
Энергетические соотношения в связанных контурах.
Рассмотрим, как распределяется мощность между связанными контурами в зависимости от степени их связи. При этом анализировать будем типичный для практики случаи, когда каждый из контуров в отдельности настроен в резонанс на частоту генератора w>0> (т. е. Х>1>= 0, Х>2>= 0) и лишь потом подбирается связь между ними. Так как обычно выходным является второй контур и с ним связаны последующие каскады приемного устройства, то задача состоит в передаче максимальной энергии во второй контур.
Для оценки эффективности передачи энергии во второй контур введем понятие к.п.д. системы двух связанных контуров как отношение мощности, выделяемой во втором контуре, к суммарной мощности в первом и втором контурах, т. е.
 (25)
(25)
где
 и
и
 Подставив в (25) значения мощностей Р>1>
и Р>2>
получим
Подставив в (25) значения мощностей Р>1>
и Р>2>
получим
 Ток I>2>
заменим его значением из (13) при Х>>=
0, т.е. I>>=I>>X>св>/r>>.
Тогда
Ток I>2>
заменим его значением из (13) при Х>>=
0, т.е. I>>=I>>X>св>/r>>.
Тогда

Из (10) следует, что X>св>/r>>=R>вн> при Х>>=0. Таким образом,
 (26)
(26)
Из курса электротехники известно, что максимальная мощность отдается в нагрузку тогда, когда внутреннее сопротивление генератора равно сопротивлению нагрузки. Для случая связанных контуров это равносильно равенству r>>=R>вн >с точки зрения передачи максимальной энергии во второй контур из первого. При этом, как видно из (26), =0.5, т. е. половина мощности теряется в первом контуре.
Настройка системы двух связанных контуров.
При желании передать во второй контур максимальную энергию, обеспечивающую и максимальны ток в нем, прибегают к настройке системы связанных контуров. Для того чтобы получить самый большой ток во втором контуре, необходимо выполнить два условия: с одной стороны, обеспечить равенство Х>1э>=0, а с другой, -r>>=R>вн>> > Первое условие может быть выполнено двумя способами: 1) настройкой системы (при наличии определенной связи между контурами) на частоту генератора изменением параметров только одного из контуров; 2) настройкой на частоту генератора сначала первого контура при разомкнутом втором, а затем подключением и настройкой второго контура при достаточно слабой связи между контурами, чтобы ослабить взаимное влияние.
Первый способ настройки называют методом частного резонанса, причем в зависимости от того, параметры первого или второго контура участвуют в настройке, достигается соответственно первый или второй частный резонанс. При частном резонансе хотя и получается максимум тока во втором контуре, но этот максимум не является самым большим, так как при обеспечении равенства Х>1э>= 0 еще не выполняется условие r>1>=R>вн >которое достигается соответствующим подбором связи между контурами. Связь, обеспечивающую максимальную мощность (ток) во втором контуре, называют оптимальной. Подбор ее производится постепенно с последующей подстройкой контура после очередной установки связи, так как при каждом изменении связи нарушается условие Х>1э>= 0 за счет изменения Х>вн>. Если до изменения связи система была настроена в резонанс изменением параметров первого контура (первый частный резонанс), то после каждого очередного изменения связи необходимо подстраивать систему в резонанс изменением параметров первого контура, чтобы все время выполнялось условие Х>1э>= Х>1э> + Х>вн>= 0.
Таким образом, при таком постепенном подборе связи с последующей подстройкой контуров может быть достигнута оптимальная связь, обеспечивающая самый большой максимум тока во втором контуре. Данный способ настройки носит название метода сложного резонанса. Проанализируем его математически.
Если обратиться к выражению для тока во втором контуре [см (14)], то при достижении, например, первого частного резонанса оно примет вид:

Далее положив, что при изменении связи (Хсв) условие Х>1э>=0 все время поддерживается неизменным подстройкой параметров первого контура, найдем оптимальное сопротивление связи (Х>св.опт>), обеспечивающее самый большой максимум тока во втором контуре (I>2махмах>). Для этого необходимо взять производную токов I>2мах> по
Х>св> и приравнять ее нулю

откуда
 ,
или
,
или
 ,
где
,
где
 .
.
Таким образом, подтверждено, что при оптимальной связи r>1>=R>вн>, причем
 (27)
(27)
Подставив значение Х>св.опт >в выражение для тока I>2mах>, можно найти самый большой максимум тока во втором контуре
 (28)
(28)
Однако на практике используют так называемый метод полного резонанса, при котором сначала достигается равенство Х>1э>= 0 по описанному второму способу настройки, когда каждый контур системы настраивается в резонанс независимо от другого. Затем подбирается оптимальная связь между контурами по самому большому току во втором контуре (I>2max max>). В случае полного резонанса при изменении связи между контурами подстройка их для выполнения условия
Х>1э>= Х>1>-Х>cв>2/Z>2>=0 нужна, так как ввиду того что Х>1>= Х>2>=0, это условие выполняется при любой связи.
Обратимся в случае полного резонанса к выражению для тока во втором контуре (14) и исследуем его на экстремум, т. е. определим оптимальную связь, обеспечивающую I>2max max >, как это было сделано при сложном резонансе. С учетом того, что Х>1>= Х>2>=0, (14) принимает вид

Взяв производную тока I>2max > по Х>св>

и приравняв ее к нулю, найдем
 или
или

где

Таким
образом, в случае полного резонанса
также подтверждено, что при оптимальной
связи r>1>=R>вн>,
причем
 При подстановке этого значения в
выражение для I>2max>
получаем
При подстановке этого значения в
выражение для I>2max>
получаем
 Как
видно из сравнения последнего выражения
с (28), значение самого большого тока во
втором контуре при сложном и полном
резонансах одинаковое, но в случае
сложного резонанса оно достигается
при большем значении Х>св.опт>,
т.е. при большей связи между контурами.
Как
видно из сравнения последнего выражения
с (28), значение самого большого тока во
втором контуре при сложном и полном
резонансах одинаковое, но в случае
сложного резонанса оно достигается
при большем значении Х>св.опт>,
т.е. при большей связи между контурами.
Прохождение радиоимпульса через двухконтурную связанную систему
Для анализа возьмем импульс с прямоугольной огибающей. Частота заполнения не модулирована и равна w>0>. Амплитуда импульса равна 1в, а Q>0>=0.
В качестве двухконтурной избирательной системы рассматривается полосовой усилитель схематически изображенный на рис. 8. Контуры идентичны, резонансные частоты контуров w>р1>=w>р2>=w>р>=w>0>. Таким бразом, в данном случае Dw = 0.

Рис. 8.
Передаточная функция такого усилителя
 (29)
(29)
где




Заменяя iW на Р, получаем
 (30)
(30)
Обратимся
к опредилению сигнала на выходе системы.
Сначала рассмотрим явления на фронте
импульса. При этом задача сводится к
включению гармонической э.д.с. в момент
t = 0.
Подставив в общее выражение спектральную
плотность S>A>(p)>
>по
формуле
 и
коэффициент передачи К>1(p)>
по формуле (30), получим
и
коэффициент передачи К>1(p)>
по формуле (30), получим

Полюсы подынтегральной функции


Определяя вычеты, получим следующее окончательное выражение для комплексной огибающей выходного сигнала (угол Q>0> принят равным нулю)
 (31)
(31)
Вчастном случае ‘критической связи’ (kQ = 1) получаем
 (32)
(32)
Множитель eip/2 учитывет сдвиг фазы выходного напряжения на 900 относительно входного сигнала.
График
 изображен
на рис. 9 (участок от t
=
0 до
t
=
T).
изображен
на рис. 9 (участок от t
=
0 до
t
=
T).

Рис. 9.
Рассмотрим теперь явления в цепи в конце импульса, начиная с момента t = T, где T – длительность импульса. Ясно, что после прекращения действия внешней силы в системе может существовать только свободное колебание. Структура этого колебания легко может быть выявлена, если прекращение импульса рассматривать как результат включения в момент t = T новой э.д.с., компенсирующей э.д.с. сигнала. Для этой компенсируещей э.д.с. решение имеет такой же вид, как и (31), но отличается только знаком, который должен быть обратным знаку правой части выражения (31), и сдвигом начала отсчета времени из нуля в точку t = T.
Так как к моменту t = T затухающую часть выражения (31) можно считать равной нулю, то комплексная огибающая результирующего сигнала на выходе для t > T должна иметь вид

Построенный
по этой формуле график
 для kQ=1
изображен на рис. 9 (участок
t
> T).
для kQ=1
изображен на рис. 9 (участок
t
> T).
литература
1. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Советское радио, 1971.
2. Комлик В.В. Радиотехника и измерения. Изд-во ‘Вища школа’, Киев, 1978.
3. Мегла Г. Техника дециметровых волн. - М.: Советское радио, 1958.
4. Григорьев А.Д. Электродинамика и техника СВЧ. - М.: Высшая школа, 1990.
5. Гинзтон Э.Л. Измерения на сантиметровых волнах. Изд-во иностранной литературы, Москва 1960.
6. Будурис Ж., Шеневье П. Цепи сверхвысоких частот. - М.: Советское радио, 1979.