Простой эффект Джозефсона

Петрозаводский Государственный Университет



















Реферат

Стационарный эффект Джозефсона:

физика и применение

дисциплина «Физика сверхпроводников»

Выполнил студент V курса

физико-технического факультета

Сержантов Д. Н.













Петрозаводск 2003

Сверхпроводимость - макроскопическое квантовое явление

При понижении температуры многие металлы и сплавы переходят в сверхпроводящее состояние. Этот переход происходит при вполне определенной для каждого материала температуре T>c> , называемой критической. Сверхпроводимость характеризуется идеальной электропроводностью (сопротивление электрическому току равно нулю, если плотность тока меньше некоторой критической величины j>c>) и идеальным диамагнетизмом (индукция магнитного поля внутри сверхпроводника равна нулю, если ее значение снаружи меньше критического В>с>).

В микроскопической теории сверхпроводимости важным моментом является объяснение достаточно сильного притяжения между двумя электронами, возникающего при поляризации кристаллической решетки. Два электрона с противоположными спинами и направлениями движения объединяются в пару, называемую куперовской (по имени американского ученого Л. Купера, впервые показавшего, что такие два электрона образуют связанное состояние). Эти пары обладают нулевым суммарным спином и поэтому являются бозе-частицами (то есть частицами, подчиняющимися статистике Бозе-Эйнштейна). Такие частицы обладают замечательным свойством: если температура ниже Т>с> , они могут скапливаться на самом нижнем энергетическом уровне (в основном состоянии). Чем больше их там соберется, тем труднее какой-либо частице выйти из этого состояния. Для этого необходимо преодолеть энергетический барьер величиной 2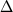 (по на каждый электрон в паре). Все частицы при этом описываются единой волновой функцией или, другими словами, когерентны. Характерное расстояние между двумя электронами в куперовской паре, называемое длиной когерентности , различно для разных сверхпроводников и может принимать значения 10-7-10-5љсм.

Таким образом, сверхпроводимость можно представить себе так. При Т < Т>с> электрический ток переносится куперовскими парами, то есть элементарными носителями тока с зарядом 2e (e - заряд электрона). При этом какой-либо частице совсем не просто рассеяться на примесном атоме или каком-либо другом дефекте кристаллической решетки металла, включая тепловые колебания ионов. Для этого ей нужно преодолеть сопротивление всех остальных подобных частиц.

Так как электрическое сопротивление равно нулю, то возбужденный в сверхпроводящем кольце ток будет существовать бесконечно долго. Электрический ток в этом случае напоминает ток, создаваемый электроном на орбите в атоме Бора: это как бы очень большая боровская орбита. Незатухающий ток и создаваемое им магнитное поле (рис. 1) не могут иметь произвольную величину, они квантуются так, что магнитный поток, пронизывающий кольцо, принимает значения, кратные элементарному кванту потока

Вб (h - постоянная Планка).

Рис. 1.Незатухающий ток и создаваемое им магнитное поле не могут иметь произвольную величину, они квантуются так, что магнитный поток, пронизывающий кольцо, принимает значения, кратные элементарному кванту потока Вб (h - постоянная Планка).

В отличие от электронов в атомах и других микрочастиц, поведение которых описывается квантовой теорией, сверхпроводимость - макроскопическое квантовое явление. Действительно, длина сверхпроводящей проволоки, по которой течет незатухающий ток, может достигать многих метров и даже километров. При этом носители тока в ней описываются единой волновой функцией. Это не единственное макроскопическое квантовое явление. Другим примером может служить сверхтекучесть в жидком гелии или в веществе нейтронных звезд.

В 1962 году появилась статья [Josephson B.D.,1962] никому до того неизвестного автора Б. Джозефсона, в которой теоретически предсказывалось существование двух удивительных эффектов: стационарного и нестационарного. Джозефсон теоретически изучал туннелирование куперовских пар из одного сверхпроводника в другой через какой-либо барьер. Прежде чем переходить к первому эффекту Джозефсона, остановимся кратко на туннелировании электронов между двумя частями металла, разделенными тонким слоем диэлектрика.

Туннельный эффект

Туннельный эффект - это типичная задача квантовой механики. Частица (например, электрон в металле) подлетает к барьеру (например, к слою диэлектрика), преодолеть который она по классическим представлениям никак не может, так как ее кинетическая энергия недостаточна, хотя в области за барьером она со своей кинетической энергией вполне могла бы существовать. Напротив, согласно квантовой механике, прохождение барьера возможно. Частица с некоторой вероятностью может как бы пройти по туннелю через классически запрещенную область, где ее потенциальная энергия как бы больше полной, то есть классическая кинетическая энергия как бы отрицательна. На самом деле с точки зрения квантовой механики для микрочастицы (электрона) справедливо соотношение неопределенностей (x - координата частицы, p - ее импульс). Когда малая неопределенность ее координаты в диэлектрике (dљ-љтолщина слоя диэлектрика) приводит к большой неопределенности ее импульса , а следовательно, и кинетической энергии p2/(2m) (m - масса частицы), то закон сохранения энергии не нарушается. Опыт показывает, что действительно между двумя металлическими обкладками, разделенными тонким слоем диэлектрика (туннельный переход), может протекать электрический ток тем больший, чем тоньше диэлектрический слой.

Стационарный эффект Джозефсона

Джозефсон рассматривал частный случай туннельного эффекта - туннелирование куперовских пар - и предсказал существование двух эффектов. Первый из них состоит в том, что через туннельный переход с тонким слоем диэлектрика, когда его толщина меньше или порядка длины когерентности (), возможно протекание сверхпроводящего тока, то есть тока без сопротивления. Предсказывалось, что критическое значение этого тока будет своеобразно зависеть от внешнего магнитного поля. Если ток через такой переход станет больше критического, то переход будет источником высокочастотного электромагнитного излучения. Это нестационарный эффект Джозефсона, который в данной работе не рассматривается..

Понадобилось немного времени, чтобы обнаружить эти эффекты экспериментально. Более того, вскоре стало ясно, что эффекты Джозефсона присущи не только туннельным переходам, но и более широкому классу объектов - сверхпроводящим слабым связям, то есть участкам сверхпроводящей цепи, в которых критический ток существенно подавлен, а размер участка порядка длины когерентности .

В основе эффектов Джозефсона лежат квантовые свойства сверхпроводящего состояния (см. выше). Действительно, сверхпроводящее состояние характеризуется когерентностью куперовских пар: эти пары электронов находятся на одном квантовом уровне и описываются общей для всех пар волновой функцией, ее амплитудой и фазой. Они когерентны как частицы света - фотоны в излучении лазера, которое также характеризуется амплитудой и фазой электромагнитной волны.

Представим теперь себе два массивных куска одного и того же сверхпроводника, полностью изолированных друг от друга. Так как оба они находятся в сверхпроводящем состоянии, каждый из них будет характеризоваться своей волновой функцией. Поскольку материалы и температуры одинаковы, модули обеих волновых функций должны совпадать, а фазы произвольны. Однако, если установить между ними хотя бы слабый контакт, например туннельный, куперовские пары будут проникать из одного куска в другой и установится фазовая когерентность. Возникнет единая волновая функция всего сверхпроводника, которую можно рассматривать как результат интерференции волновых функций двух половинок. Ниже будет показано, что сверхпроводники со слабыми связями дают уникальную возможность наблюдения фазы волновой функции в макроскопическом масштабе аналогично проявлению фазы электромагнитной волны в явлениях интерференции в оптике.

Следует заметить, что слабая связь между двумя сверхпроводниками - это просто удобный объект для обнаружения интерференционных эффектов. Однако такие эффекты были известны сравнительно давно. Один из ярких примеров - квантование магнитного потока и тока в сверхпроводящем кольце. Действительно, сверхпроводящий ток может принимать только такие значения, при которых на длине кольца может уложиться целое число длин волн волновой функции сверхпроводящих электронов, то есть при обходе по контуру кольца волновая функция в каждой точке попадает в фазу сама с собой. Еще раз видна полная аналогия с квантованием орбит в атоме Бора.

Как уже упоминалось, стационарный эффект Джозефсона состоит в том, что достаточно слабый ток I (меньший критического тока слабой связи I>c>) протекает без сопротивления, то есть на ней не происходит падения напряжения. Джозефсон получил следующее выражение для тока I:

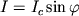, (1)

где - разность фаз волновых функций по разные стороны слабой связи. В своей работе [Josephson B.D.,1962] Джозефсон предсказал, что в области диэлектрической прослойки будут интерферировать когерентные токи, исходящие из обоих сверхпроводников, так же как световые волны от двух когерентных источников. Поэтому результирующий ток оказывается пропорциональным синусу разности фаз.

Через год после предсказания Джозефсона этот эффект проверил прямым экспериментом Дж. Роуэлл. В туннельных экспериментах такого рода, когда диэлектрическая прослойка очень тонка, основная трудность состоит в устранении контакта металлических обкладок из-за дефектов диэлектрика. Надо каким-то образом доказать, что наблюдаемый ток не является следствием тривиальных закороток, а действительно является туннельным током. Для этого Дж. Роуэлл поместил туннельный переход в магнитное поле, направленное вдоль плоскости барьера. Естественно, что магнитное поле не может влиять на закоротки и в этом случае ток практически не изменился бы. Однако даже очень слабое магнитное поле влияло на ток, причем совершенно нетривиальным образом.

Дело в том, что магнитное поле изменяет фазу волновой функции сверхпроводящих электронов. Поскольку в этом, пожалуй, наиболее ярко проявляется макроскопический квантовый характер сверхпроводящего состояния и эти явления продолжают оставаться в центре внимания и в настоящее время, рассмотрим их более подробно.

Квантовая интерференция

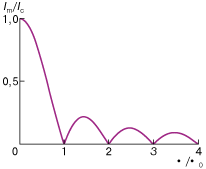
Уже в первом эксперименте было обнаружено, что максимальный сверхпроводящий ток I>c> в магнитном поле, параллельном плоскости контакта, немонотонно зависит (с периодом, равным кванту потока ) от величины магнитного потока , проникающего в контакт. Эта зависимость показана на рис. 2. Как видно из рисунка, в случае, когда поток равен целому числу квантов , происходит компенсация токов, текущих в противоположные стороны в разных точках контакта, и результирующий критический ток оказывается равным нулю. Этот график аналогичен зависимости интенсивности света на экране при дифракции на одиночной щели от расстояния до центральной точки и наглядно демонстрирует волновые свойства сверхпроводящих токов.

Рис. 2.Зависимость критического тока I>m> (нормированного на критический ток при отсутствии поля I>c>) джозефсоновского контакта от величины потока внешнего магнитного поля

Чтобы рассмотрение этого явления стало более простым, включим туннельный контакт в сверхпроводящий контур (кольцо). Магнитный поток через площадь сверхпроводящего кольца (не содержащего контакта) строго постоянен. Его значение, как уже говорилось, квантуется. Оно равно целому числу квантов , и изменить его, не переводя кольцо в нормальное состояние, невозможно. Но если кольцо содержит слабую связь, то магнитный поток может меняться - кванты потока проникают в контур через это слабое место.

Посмотрим, как при изменении внешнего магнитного поля меняется величина потока и тока I в кольце со слабой связью. Пусть сначала внешнее поле и ток в контуре равны нулю (рис. 3, а). Поток при этом тоже равен нулю. Увеличим внешнее поле - по закону индукции Фарадея в контуре появится сверхпроводящий ток, своим магнитным полем по закону Ленца компенсирующий внешний поток. Так будет происходить, пока ток в контуре не станет равным критическому току контакта I>c> (рис. 3, б ). Для простоты рассмотрения выберем площадь кольца такой, чтобы при I = I>c> внешнее поле создавало поток , равный половине кванта потока: .

Рис. 3.Сверхпроводящий контур с джозефсоновским элементом во внешнем магнитном поле

Рис. 4.Двухконтактный интерферометр. Схема (а) и зависимость критического тока от величины магнитного потока (б )

Как только ток станет больше I>c> , сверхпроводимость в контакте нарушится и в контур войдет квант потока (рис. 3, в). При этом отношение скачком увеличится на единицу, а направление тока изменится на противоположное, хотя его величина останется прежней I>c> . Действительно, если до вхождения кванта потока ток I>c> полностью экранировал внешний поток , то после вхождения он должен усиливать внешний поток до значения . Таким образом, контур перешел в новое квантовое состояние.

При дальнейшем увеличении внешнего поля ток в кольце будет уменьшаться, а поток будет оставаться равным . Ток обратится в нуль, когда внешний поток станет равным (рис. 3, г), а затем ток потечет в обратном направлении, частично экранируя внешний поток. При внешнем потоке ток опять станет равным I>c> , сверхпроводимость нарушится, войдет следующий квант потока и т.д. Ступенчатый характер рассмотренных зависимостей позволяет почувствовать отдельные кванты потока, а ведь эта величина очень мала, всего лишь порядка 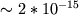Вб.

Особенно ярко когерентные свойства сверхпроводящего состояния проявляются при включении в контур двух джозефсоновских контактов (рис. 4, а). Полный ток I при этом определяется интерференцией токов, протекающих через контакты:

(2)

где и - скачки фаз волновых функций на переходах, а критические токи обоих контактов для простоты взяты одинаковыми и равными I>c> . В результате критический ток I>m> периодически зависит от внешнего магнитного поля и обращается в нуль, когда поток равен полуцелому числу квантов (рис. 4, б ). Эта зависимость в точности соответствует оптическому аналогу - зависимости интенсивности света на экране от расстояния при дифракции на двух щелях.

Применение

С 1911 по 1986 было исследовано очень много сверхпроводящих металлов и сплавов, но наивысшая измеренная температура перехода составляла 23,2 К. Для охлаждения до такой температуры требовался дорогостоящий жидкий гелий (4Не). Поэтому наиболее успешные применения сверхпроводимости оставались на уровне лабораторных экспериментов, для которых не требуется больших количеств жидкого гелия.

В конце 1986 К.Мюллер (Швейцария) и Й.Беднорц (Германия), работая в исследовательской лаборатории IBM в Цюрихе, обнаружили, что керамический проводник, построенный из атомов лантана, бария, меди и кислорода, имеет температуру перехода в сверхпроводящее состояние, равную 35 К. Вскоре исследовательские группы в разных странах мира изготовили керамические материалы с температурой перехода от 90 до 100 К, которые способны оставаться сверхпроводниками (2-го рода, см. выше) в магнитных полях до 200 кГс.

Керамические сверхпроводники весьма перспективны в плане крупномасштабных применений, главным образом по той причине, что их можно изучать и использовать при охлаждении сравнительно недорогим жидким азотом.

Лабораторные применения. Первым промышленным применением сверхпроводимости было создание сверхпроводящих магнитов с высокими критическими полями. Доступные сверхпроводящие магниты позволили получить к середине 1960-х годов магнитные поля выше 100 кГс даже в небольших лабораториях. Ранее создание таких полей с помощью обычных электромагнитов требовало очень больших количеств электроэнергии для поддержания электрического тока в обмотках и огромного количества воды для их охлаждения.

Следующее практическое применение сверхпроводимости относится к технике чувствительных электронных приборов. Экспериментальные образцы приборов с контактом Джозефсона могут обнаруживать напряжения порядка 10–15 Вт. Магнитометры, способные обнаруживать магнитные поля порядка 10–9 Гс, используются при изучении магнитных материалов, а также в медицинских магнитокардиографах. Чрезвычайно чувствительные детекторы вариаций силы тяжести могут применяться в различных областях геофизики.

Техника сверхпроводимости и особенно контакты Джозефсона оказывают все большее влияние на метрологию. С помощью джозефсоновских контактов создан стандарт 1 В (об этом ниже). Был разработан также первичный термометр для криогенной области, в которой резкие переходы в некоторых веществах используются для получения реперных (постоянных) точек температуры. Новая техника используется в компараторах тока, для измерений радиочастотной мощности и коэффициента поглощения, а также для измерений частоты. Она применяется также в фундаментальных исследованиях, таких, как измерение дробных зарядов атомных частиц и проверка теории относительности.

Сверхпроводимость будет широко использоваться в компьютерных технологиях. Здесь сверхпроводящие элементы могут обеспечивать очень малые времена переключения, ничтожные потери мощности при использовании тонкопленочных элементов и большие объемные плотности монтажа схем. Разрабатываются опытные образцы тонкопленочных джозефсоновских контактов в схемах, содержащих сотни логических элементов и элементов памяти.

Сверхпроводниковый суперкомпьютер

Идея использования джозефсоновских переходов в качестве элементной базы компьютеров появилась уже довольно давно. И если задача получения малых размеров переходов (плотность упаковки) и малого тепловыделения (в сверхпроводящем состоянии тепло вообще не рассеивается) довольно легко решается, то сверхвысокого быстродействия достичь долго не удавалось.

Принципиально новое решение этой проблемы было впервые предложено в группе профессора К.К. Лихарева в МГУ. Для обработки и запоминания информации здесь используется квант магнитного потока, то есть нуль и единица - отсутствие или наличие в джозефсоновской ячейке одного кванта потока. Логические элементы с джозефсоновскими переходами, в которых проводится квантование магнитного потока, называются квантронами. Расчеты и эксперименты показывают, что квантроны обладают очень высоким быстродействием, достигающим значений 1012 операций в секунду. Однако они не подчиняются традиционным правилам схемотехники и их следует применять в схемах нового типа. Здесь информация передается от одного элемента к другому с помощью кванта магнитного потока, поэтому обязательным условием является близкое расположение элементов. Характерные расстояния, разделяющие при этом элементы, достигают величин порядка десятых долей микрона. Такие схемы выгодно применять, например, при создании регистров сдвига - устройств с передачей информации вдоль периодической структуры элементов логики, причем информация смещается на единичный период при введении или изъятии единичного кванта потока.

Установка на основе эффекта Джозефсона для воспроизведения единицы напряжения постоянного тока

Во ВНИИФТРИ создана установка на основе матрицы джозефсоновских переходов для воспроизведения единицы напряжения постоянного тока.

Установка предназначена для калибровки и поверки многоразрядных аналого-цифровых преобразователей (АЦП) в интегральном исполнении, может также использоваться для калибровки и поверки высокоточных мер напряжения и цифровых вольтметров.

Основным элементом установки является матрица джозефсоновских переходов, изготовленная в РТВ (Германия). Использование эффекта Джозефсона обеспечивает высокую точность воспроизведения напряжения.

Установка состоит из криозонда с джозефсоновской матрицей, СВЧ генератора (длина волны ~ 4 мм) с системой фазовой автоподстройки частоты, рубидиевого стандарта частоты, характериографа, транспортируемого гелиевого дюара.

Список литературы:

    http://phys.web.ru/db/msg.html?mid=1181649&uri=page1.html

(pdf-версия на http://www.issep.rssi.ru/sej_str/ST988.htm)

    http://www.issep.rssi.ru/pdf/0108_083.pdf

    http://www.extech.ru/src/src_rus/catalog/10/technol/tecH21.htm